基于混合优化匹配追踪算法的礁滩储层流体识别方法

2020-06-19朱宝衡

复杂油气藏 2020年1期

朱宝衡

（中国石化上海海洋油气分公司勘探开发研究院，上海200120）

生物礁作为碳酸盐岩沉积中的一特殊油气储集体，常具有物性好、产能高等特点。预测生物礁储层的流体分布特征对于生物礁储层的勘探开发具有重要的意义。对于叠后地震数据而言，一般通过寻找流体敏感属性来预测流体，如低频阴影、流体活动性等，而精确的时频分析技术是利用这些属性识别流体的基础。目前众多的时频分析方法中以匹配追踪（MP）算法时频分辨率最高,匹配追踪（MP）算法最早是由Mallat［1］等提出的，后来Marfurt［2］等提出了基于Gabor型时频原子的经典匹配追踪自适应分解算法。国内外学者为了提高匹配追踪算法计算效率提出了大量快速算法，Liu等将地震信号的瞬时特征引入到匹配追踪算法中［3］，Wang提出三步法实现匹配追踪［4］，张繁昌等提出了双参数快速匹配追踪算法［5］，张显文等提出两步法匹配追踪算法，提高了匹配追踪算法的效率，并用于河道砂体识别、随机噪声消除、生物礁储层含气储层烃类检测和时频分析等［6］。

常规的匹配追踪算法需要全方位扫描子波库，计算量大，效率低，不适用于海量的地震数据处理。另外，为了更好分析地震信号时频谱，了解其非平稳特性，我们选择具有能量吸收和速度频散的地震信号Morlet小波原子作为基本匹配子波。本文提出结合局部优化的BFGS算法及全局优化的粒子群算法的混合优化算法，一次性计算描述Morlet 小波的五个参数，能够更好地适应信号的结构特征。常规匹配追踪算法具有较强的多解性，为此混合优化的匹配追踪算法（Hybrid Optimization Matching Pursuit Algorithm，HO-MP）将残差信号能量与分解子波能量的比值最小定义为目标函数，以降低多解性，并加快收敛速度。在混合优化匹配追踪算法研究的基础上，分析碳酸盐岩含气储层中流体活动属性的变化规律，对碳酸盐岩礁滩相储层流体进行识别。并以楚-萨雷苏盆地的典型生物礁储层为例，验证了该方法的实用性，结果表明混合优化匹配追踪算法的时频分辨率更高，对于流体的识别更加准确。

1 方法原理

1.1 流体活动因子

当地震波穿过地下介质时，经过波前扩散和地层的滤波作用后，振幅能量会发生一定的变化，低频能量比高频能量衰减快，Silin等人（2004）对弹性和弹性流体饱和多孔介质界面的地震反射进行了低频渐近分析。此外，他们提出了一个推导谐波解方程过滤理论，并介绍了无量纲小参数的渐近分析，然后建立了低频区流体饱和多孔介质地震反射的渐近表示［7］。 Goloshubin（2006）等将流体活动性属性表示为地层含流体时地震振幅与频率的比值［8］，如图1所示，用于对碳酸盐岩含气性储层识别。

图1 流体活动因子原理示意图

利用公式（1）对频率求导，可以得到：

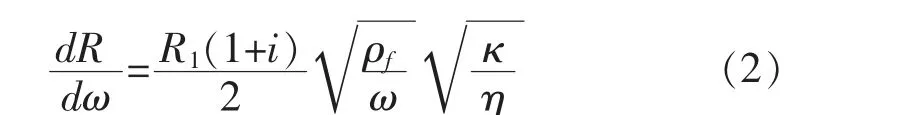
方程（3）意味着储层流体流动性和频率反射系数的一阶导数成正比。地震信号经过时频分解后的瞬时频谱振幅或相对于一个公共频率的能量，可以真实反映出在该频率下地震反射的能量或振幅。因此，通过用瞬时频谱振幅代替实际频率下的反射系数R，我们得到：

1.2 常规匹配追踪基本原理

匹配追踪算法从一个完备的子波原子库出发，采用某种策略每次选取与地震道信号最匹配的基（也称为原子域或时频原子），创建超完备子波库所使用的子波原子基与原始信号越相似，则分解效果越好，最终将地震道信号表示为若干时频原子的线性组合，实现地震信号的高精度时频分解［9-10］。

MP算法每次迭代提取最匹配的Morlet小波原子mγn，Morlet小波（如图2）与地震子波类似，地震信号能够由不同频率、相位和尺度的小波叠加组成，则经过次迭代后，地震信号可以表示为

式中，an是mγn的振幅，R（N）f 是残差，并且R（0）f=S（t）。

匹配追踪算法步骤如下：

①创建morlet小波集

在实际应用中，首先建立一个子波集。如何建立一个合理的完备的子波集对地震信号能否精确匹配分解至关重要。由于morlet小波具有衰减特征，与地震信号的子波具有相似性，所以本文采用morlet小波构建冗余的子波集。

图2 Morlet小波示意

②初步求取匹配morlet小波的参数γn=｛τn，fn，σn，φn｝。

在第n次迭代时，首先对单道数据做希尔伯特变换，求取复地震道，搜索复地震道最大振幅所对应的时间值，将其定为匹配小波中心时间τn的初始值，该时刻的瞬时频率为fn，瞬时相位为φn，然后应用优化原理搜索衰减参数σn的初始值。

③优选匹配morlet小波的参数γn=｛τn，fn，σn，φn，an｝

其中，D为冗余的morlet小波集；〈R（N）f ，mγn〉为内积。

④匹配原子的维格纳威尔分布

把信号用一些波原子的组合来表示，接着求取它们相对应的Wigner-Ville分布，从而得到整个地震信号准确的时频分布。对于Morlet小波，相比于广义S变换（GST），利用魏格纳（WVD）分布计算时频谱能够同时获得高精度的时间域和频率域分辨率（如图3）：

图3 Morlet小波GST与WVD时频谱对比

1.3 混合优化匹配追踪

常规的匹配追踪算法是一种不断迭代、寻求最佳匹配的贪婪算法，子波库中的可供选择用于匹配的子波是固定的，对子波库的全方位遍历搜索，不停的迭代，最后才能达到一定的匹配度，这样导致搜索效率很低，不适合于大规模三维地震资料处理。针对以上问题，通过对全局优化粒子群算法（PSO）和局部优化BFGS算法的研究，将PSO算法和BFGS算法结合，取长补短，得到混合优化匹配追踪算法，能克服传统匹配追踪计算效率低的问题，更好的对地震信号进行准确高效的时频分解［11-19］。

1.3.1 粒子群优化算法

PSO算法是通过不断迭代寻找最优解的新型热门算法。算法中假设鸟为没有质量和体积的微粒，并延伸到N维空间，且设：

xi=（x1，x2，…xN）：表示粒子在N维空间的位置矢量；

Vi=（V1，V2，…VN）：表示飞行速度。

并设Pbest为粒子最佳位置，xi为粒子的当前位置，粒子下一步的飞行不断由前面的经验来控制。PSO算法假设最开始的粒子是随机散布的，然后利用公式（7）、（8）不断寻找新的速度位置。

因为粒子搜索方向存在局限性，不能保证都收敛到全局最优解（概率1）［11］。

1.3.2 BFGS算法

BFGS算法是一种具有二次终止和整体超线性收敛的拟牛顿-共轭方法，其收敛速度比梯度最速下降法的线性收敛速度快得多，受舍入误差影响小，综合BFGS算法上述的优点，利用BFGS算法求解min（f（x））流程为：

第一步：确定维数N，收敛精度ε，并给出初始值，x0∈Rn，k=0；

第二步：求取gk=▽f（xk），若gk≤ε，则令x*=x0，f*=f（x0），算法停止，否则计算dk=-HKgk；

第三步：沿着方向dk做线性搜索求取ak＞0且令xk+1=xk+akdk；

第四步：校正HK、HK+1产生使得拟牛顿条件成立，其中：

第五步：再次让k=k+1，进入第二步。

在求取计算时，初始Hesse（逆近似H0）取单位矩阵［11］。

1.3.3 混合算法求解策略

粒子群优化算法是一种高效的随机全局优化算法，但是后期收敛速度慢，甚至处于停滞状态。BFGS方法是一种好的局部优化方法，但是其优化结果的好坏取决于初始位置的选择。通过对以上PSO算法和BFGS方法的研究发现，单独使用其中的任何一种算法都存在一定的缺点，达不到好的时频分析效果，如果利用具有全局搜索能力的粒子群算法提供给BFGS方法初始解位置，就能优势互补。混合优化算法综合PSO算法和BFGS算法优越性，提高时频分析的效果和精度［11］。BFGS算法搜索过程中设置最大搜索次数，一旦超出，则说明算法已陷入局部最优，与此同时也说明上次粒子群优化结果不是BFGS算法的理想的初始值。在利用BFGS算法时，且当gk+1≤ε时，即在计算的过程中，当结果值大于给定理想值时，我们利用算出的来求得用于下次计算的，如此不断重复，当算出的结果值小于给定的理想值时，就生成新种群空间：

式（10）中c为调节常数，rand()∈（0，1）。

1.4 MP和HO-MP的有效性对比分析

1.4.1 MP和HO-MP理论模型测试

为了检验结合PSO算法和BFGS算法的混合优化匹配追踪算法（HO-MP）在求取Morlet小波5参数(振幅、相位、时移、尺度、主频)高效精准性以及时频分析等方面的优越性，利用理论合成信号进行测试，图4a为理论信号（含随机噪声）；图4b为匹配分解得到的morlet小波；图4c为重构信号；图5、图6为MP和HO-MP分解重构信号的波形（图5a，6a）、频谱（图5b，6b）与原信号的对比，分析可知，无论在时间域还是在频率域，HO-MP相比于MP对信号的还原度都更高，且信噪比有一定程度的提高，证明了利用Morlet小波的混合优化匹配追踪有明显的优越性。

图4 理论信号的匹配分解与重构

图5 MP-理论、重构信号的波形、频率对比

图6 HO-MP-理论、重构信号的波形、频率对比

对图4中的模型信号分别应用MP和HO-MP算法，得到它的时频谱变化特征，如图7所示。

通过上面研究可知，MP和HO-MP算法都可以准确地分解出地震信号的时频谱分布特征，HO-MP算法的聚焦性更好，受噪声影响更少，更适用于地震复杂信号时频特征分析。

1.4.2 MP和HO-MP计算效率对比

表1统计了MP和HO-MP算法计算模型信号频谱分布的计算效率，表中数据说明，MP和HO-MP算法的计算用时相差不大，但MP算法的计算效率低于HO-MP，因为MP算法在求解的过程中需要反复迭代，当地震记录的结构比较简单时，20次迭代后，信号的全局结构才可以匹配出来。当地震数据为海量时，这就要对信号进行多次匹配分解，导致MP的计算效率低于HO-MP。

图7 模型信号时频分析应用效果分析

表1 模型信号时频分析计算效率分析

2 Tam研究区碳酸盐岩含气性检测

2.1 Tam研究区地质特征

楚-萨雷苏盆地是一个非常规致密叠复连续含气盆地，发育了上古生代碎屑岩、碳酸盐岩混合地层。 Tam研究区位于楚-萨雷苏盆地中部，研究区广泛发育碳酸盐岩生物礁、滩体，具有很大的勘探潜力，石炭系有利储层主要位于开阔台地、台地边缘礁-滩复合体、台内点礁和共生滩（图8）。研究区储层非均质性强、结构复杂、成因多样，给储层的识别带来了一定的困难。常规时频率分析方法（如广义S变换、常规匹配追踪），不能满足研究区的精度要求。为此，利用Tam研究区现有的常规基础资料（地震、测井、地质），通过对目的层和井旁道分析确定计算流体活动属性的频率范围（低频段），这里对采集的地震数据要有好的频带范围，低频在这里尤为重要，不同地震频率段识别含气储层的敏感性不同，这是第一步也至关重要。第二步是对地震数据应用时频谱分析技术，常规的匹配追踪算法具有计算效率低和聚焦性差的缺点，针对以上两个问题，高精度混合优化的匹配追踪算法都做了优化改进。算法成功的关键之一是选取适合于信号分析的时频原子，这里我们选择与地震子波具有良好的相似性的Morlet小波，提高了时频聚焦性；关键之二是精确地获取用于描述时频原子的参数，而混合优化匹配追踪算法综合了粒子群优化算法和BFGS算法的优点，在整个解空间中搜索最优的时频原子控制参数，这点不同于常规匹配追踪的遍历搜索，同时不再依赖于复数道分析确定时频原子的振幅、频率和相位的初值，提高了匹配追踪的精确度，并使得匹配追踪算法的计算效率得以大幅度提高；关键之三是应用局部函数的解析表达式和根据信噪比确定算法的停止准则，能够进一步地提高计算效率。选择不同的子波尺度因子和剩余能量占原始信号能量的百分比，能够有效地压制噪声；关键之四是提取平面和剖面的流体活动属性，再对含气性礁滩相储层纵向和横向展布进行分析和预测。

图8 Tam区礁滩分布情况

图9 礁滩储层流体识别技术流程

图10 Tam区Tam1与Tam5井联井地震剖面

图10为礁滩相在Tam1和Tam5井联井地震剖面上的特征，从图中可以看出礁滩相储层外形呈丘状反射，内部呈弱的杂乱反射，礁体两翼及顶部呈现连续性较强的反射，强反射特征均为地震波从高速膏盐层进入低速泥灰岩、灰岩段界面的地震反射特征。

2.2 碳酸盐礁滩体含气性检测

为验证混合优化匹配追踪分解的实用性，结合研究区实际地震资料，利用常规匹配追踪（MP）和高精度混合优化匹配追踪（HO-MP）分别对Tam区进行流体检测，以预测礁滩相储层流体特征。图11为Tam1与Tam5井常规匹配追踪（MP）流体检测联井地震剖面结果，发现在Tam5井和Tam1井流体因子剖面上礁滩部位有一定的异常值，表明储层流体较为发育，但整体分辨率较低。图12为高精度混合优化匹配追踪（HO-MP）流体检测结果，流体因子剖面上礁滩部位有非常大的异常值，储层流体发育，高精度混合优化匹配追踪（HO-MP）分辨率明显高于常规匹配追踪（MP）。钻后结果显示含气储层深度位置与流体因子参数显示的深度位置一致，且钻遇了礁体，与预测结果吻合。

基于叠后储层预测与流体结合的思路，结合地质的认识，Tam6井同样在地震剖面（图13）有礁滩显示，流体因子参数剖面上在滩的位置显示有非常大的异常值，实际应用结果表明混合优化匹配追踪（HO-MP）在研究区应用效果较好，可以作为寻找礁滩相含气储层的一种新的有效方法。