线控转向系统路感摩擦补偿研究
2020-06-19胡延平朱天阳蒋鹏飞
胡延平,朱天阳,蒋鹏飞,刘 菲,陈 韵
(1.合肥工业大学 机械工程学院,安徽 合肥 230009; 2.合肥工业大学 汽车与交通工程学院,安徽 合肥 230009)
0 引 言
线控转向(steer-by-wire,SBW)系统由于取消了转向盘和转向执行机构之间的机械连接,使地面作用在车轮上的力矩不能通过直接的方式传递给方向盘,需要控制路感电机进行模拟[1-2]。但由于SBW系统转向盘总成内部组成部件少,造成转动时固有摩擦力矩很小,与传统机械转向系统差别较大[3];且由于生产制造工艺的差异和装配的误差,使得同型号的转向系统内部摩擦力矩也存在明显差异,若不消除则必然造成路感方面的差异。因此,为保证路感设计时转向盘力矩的真实性和一致性,对转向盘总成进行合理的摩擦力矩补偿显得尤为重要。
文献[3]在研究电子助力转向(eletric power streering,EPS)系统助力控制算法的基础上,对SBW路感设计提出了包括助力控制、回正控制、阻尼控制和限位控制的综合模拟控制算法,但没有对摩擦补偿控制进行研究,使最终路感的仿真和试验结果与EPS转向系统差别较大;文献[4-6]在SBW系统路感设计时考虑到固有摩擦力矩较小的缺点,加入了定摩擦补偿策略,但没有考虑固有摩擦力矩的差异化;文献[7]对于EPS转向系统摩擦力矩的差异提出了利用径向基神经网络模型进行消除,仿真和试验结果表明该模型能够有效消除固有摩擦力矩差异性的影响,但模型单一、需要大量的训练数据且计算量大;文献[8-10]均使用基于摩擦模型的补偿策略,分别为LuGre模型、Stribeck模型、GMS模型,但对于这些模型各参数的获取难度大,并且不能根据系统之间的个体化差异进行动态补偿。
本文对SBW系统的组成和控制进行了简要的概括,在路感的设计中包含了理想反馈力矩、阻尼力矩、限位力矩和摩擦补偿力矩;针对SBW系统摩擦力矩小且差异化明显的特点,设计了改进型库伦摩擦模型和GA-BP神经网络模型相结合的摩擦力矩补偿策略;并通过Carsim/Simulink联合仿真和硬件在环试验共同验证该摩擦补偿算法的有效性。
1 SBW系统模型
SBW系统主要是由机械结构和电子控制单元组成的。在机械结构方面分为转向盘总成和转向执行总成两大模块。电子控制单元主要包括电源系统、路感电机控制器、转向电机控制器和故障诊断及报警系统等。SBW系统结构示意图如图1所示。
SBW系统因其结构特点,无法像传统转向系统直接通过机械连接的方式获取车轮与路面的反馈力矩,而是由传感器实时采集汽车的行驶状态、转向盘和路面信息,通过控制器统一处理后,控制路感电机模拟出较为真实的路面反馈力矩;在转向控制方面,将方向盘转角信号和前轮转向信号实时传递给转向控制器,实现对车轮转角的闭环控制,同时转向控制器也采集车速、横摆角速度和侧向加速度等信号,对转向过程进行优化[11]。
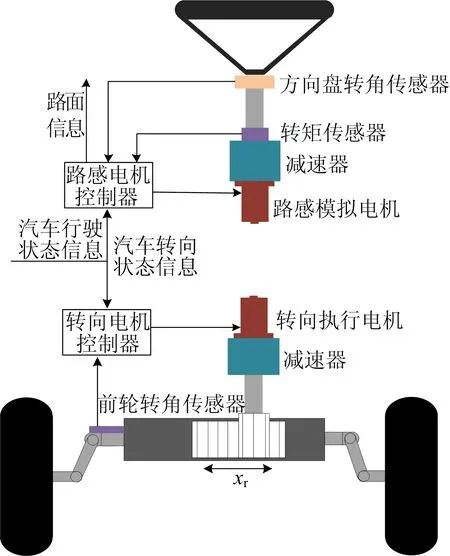
图1 SBW系统结构示意图
2 SBW系统路感组成
对于传统机械连接的转向系统,转向盘力矩受车速、路面附着系数、方向盘转角及转速的影响较大。本文研究SBW系统转向盘力矩时,在考虑上述因素之外,还考虑了高速行驶过程中的阻尼力矩、转向盘总成摩擦补偿力矩和对转向系统起限位作用的限位力矩。最终得到的SBW系统路感力矩总成为:
Td=Tlx+Tzn+Tlim+Tmx
(1)
其中,Td为转向盘总力矩;Tlx为理想反馈力矩;Tzn为阻尼力矩;Tlim为限位力矩;Tmx为摩擦补偿力矩。
2.1 理想反馈力矩
由图1可知,转向盘总成和转向执行总成之间信息能够相互传递,因此路感电机控制器可以实时采集转向执行电机的电流值,该值能够准确反映转向轮负载的变化情况。对转向电机的输出转矩和转向负载进行等效处理后,即可得到理想的反馈力矩,驾驶员通过该力矩就能够准确感知路面状况、轮胎特性和回正力矩的变化情况。
转向执行电机工作时,电机电流值与转向负载成正比例关系,负载的大小决定了电机转矩和电流的大小,同时也间接决定了理想反馈力矩的大小。理想反馈力矩动力学方程表示如下:
TH=kHIH
(2)
Tlx=TH-TE
(3)
(4)
其中,TH为转向电机电磁力矩;kH为转向电机电磁力矩系数;IH为转向电机电流;TE为传统转向系统阻力控制力矩;Ksw为方向盘转角增益;θsw为方向盘转角;Kv为速度增益;v为车速。
2.2 阻尼力矩
汽车在高速行驶时,驾驶员输入较小的方向盘转角就可能导致侧向加速度发生较大变化,并可能引发车辆的失稳,因此在路感力矩中加入阻尼力矩,可对驾驶员在高速条件下转向起到阻碍作用,避免发生较大转角。在设计该力矩时,认为它与方向盘角速度成正比例关系,并随着车速的增大而增大[12],其力矩模型表示如下:
(5)
(6)
其中,kznl为低速阻尼调节系数;kznh为高速阻尼调节系数;v1为临界车速。
2.3 限位力矩
对于传统汽车转向系统,前轮转角达到极值后,限位力矩会通过相连的机械部件传递给驾驶员,使驾驶员准确感知到车轮已经转动到极限位置。而对于SBW系统,转向盘可以无限制地任意转动。为了也让驾驶员通过转向盘的反馈力矩感知车轮是否转到极限位置,在方向盘转角所允许的最大位置处加上限位控制力矩,其表达式如下:
(7)
其中,klim为限位力矩系数;θlim为方向盘转角的极大值。
2.4 摩擦补偿力矩
机械连接的转向系统组成部件较多,连接相对复杂,在转动时能感受到明显的摩擦力矩。而SBW系统转向盘总成组成部件少且连接简单,内部摩擦力矩为0.1~0.3 N·m,远小于机械连接转向系统的内部摩擦力矩,若不对其进行摩擦补偿,则最终仿真和试验的路感力矩与传统转向系统操纵力存在很大差异[3]。
因此,本文对SBW系统转向盘总成的摩擦力矩进行补偿,主要分为2个部分。首先利用改进的库伦摩擦模型对路感进行摩擦补偿,主要目的是使补偿后的转向盘力矩与EPS转向系统相类似;然后再利用基于遗传算法(genetic algorithm,GA)的反向传播(back propagation,BP)神经网络模型对固有摩擦力矩进行补偿,其目的是对转向盘总成的固有摩擦力矩进行高精度逼近,并计算出相应的电流值给路感电机抵消固有摩擦力矩对路感的影响,消除转向盘总成因制造和装配的差异而造成路感力矩的不一致性。
3 摩擦补偿力矩设计
3.1 改进型库伦摩擦补偿
对于SBW系统,驾驶员在转动方向盘过程中所能感受到的摩擦力矩是由管柱和电机等部件产生的,该力矩值较小,若不进行有效的摩擦补偿则会导致路感力矩的失真。本文选用改进型的库伦摩擦模型对转向盘总成摩擦力矩进行补偿,即在转速为0时选用双曲正切函数来实现力矩的平滑连接[2-3]。相对于原库伦摩擦模型,改进后的模型不仅能够补偿转向盘角速度在0时的摩擦力矩,同时也保证了转角速度在0附近处摩擦补偿力矩的连续变化,避免此位置补偿数据的抖动而影响手感。
库伦摩擦补偿模型如图2所示。
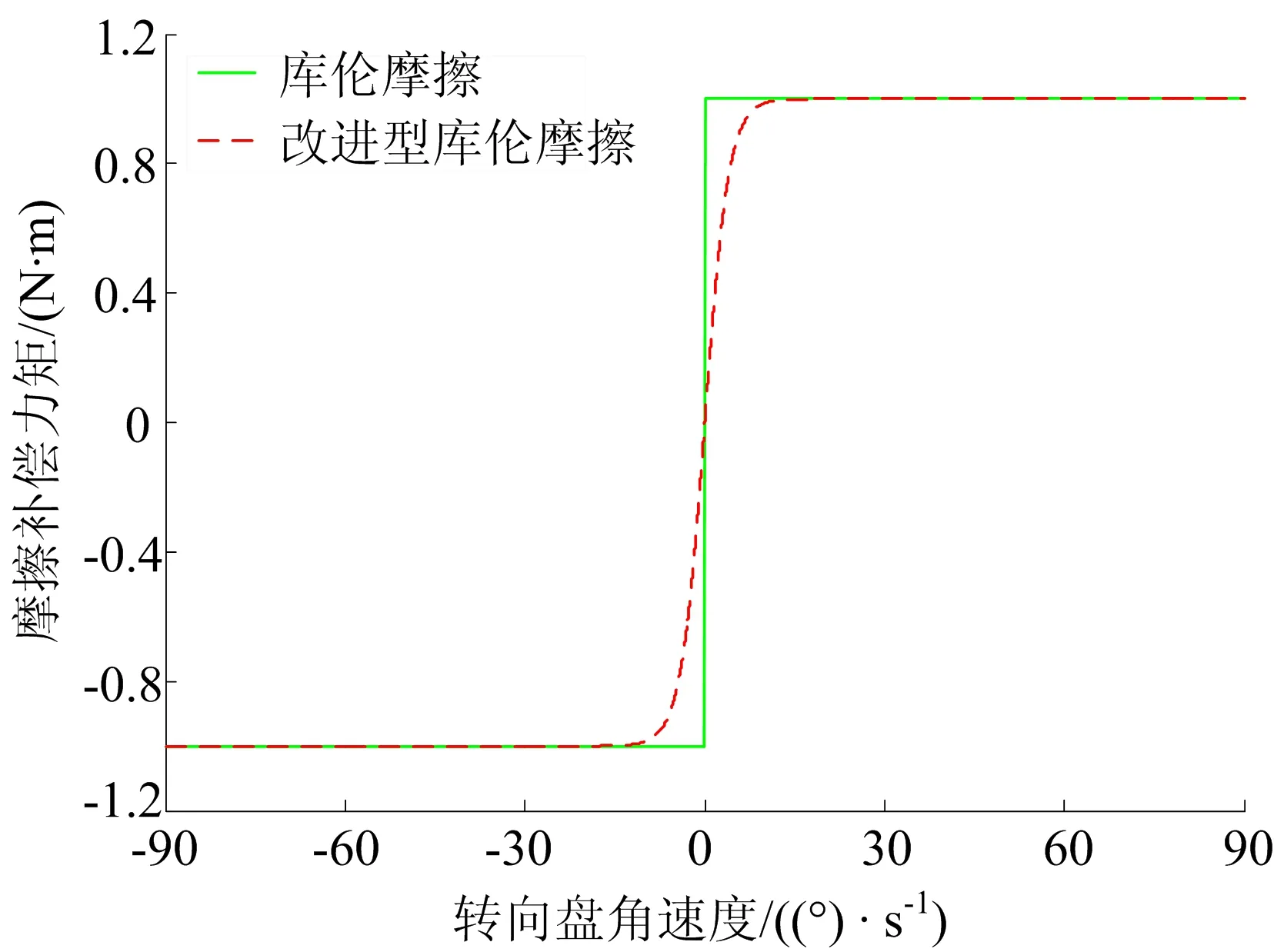
图2 库伦摩擦补偿模型
摩擦补偿力矩的表达式为:
(8)
其中,Cmx为库伦摩擦力矩;amx为梯度变化系数。
3.2 GA-BP神经网络的固有摩擦力矩补偿
3.2.1 固有摩擦力矩补偿原理
采用神经网络方法对转向盘总成固有摩擦力矩补偿的原理如图3所示。
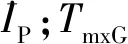
为得到GA-BP神经网络训练的理想数据,在Matlab中建立SBW系统路感模型和PID电流跟踪控制器,利用随机函数随机产生0.1~0.3 N·m的固有摩擦力矩,并在Carsim中设置各种不同的车速进行多组仿真实验,经公式计算后即可得到大量电机电流和摩擦补偿电流的变化数据。
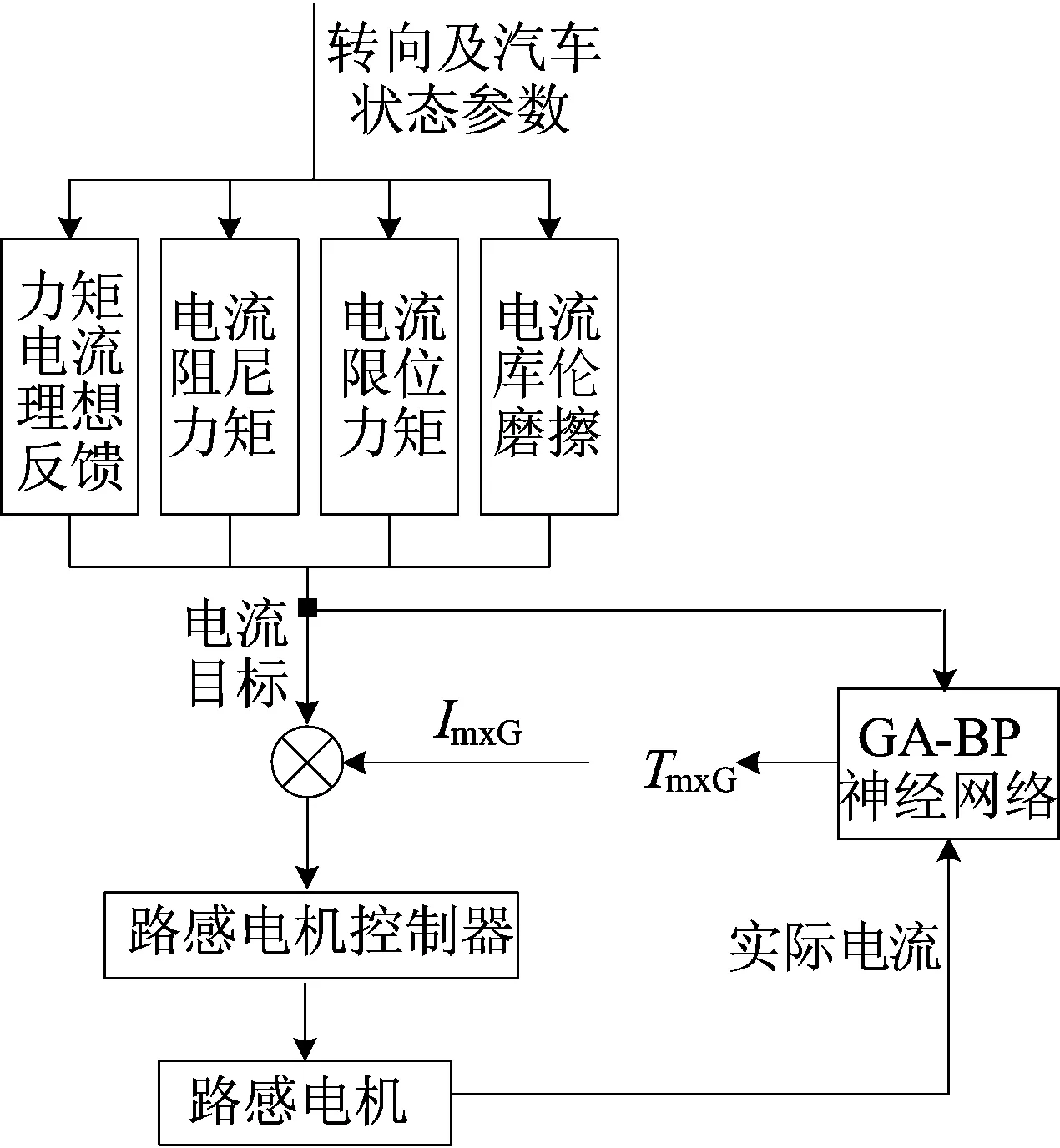
图3 固有摩擦力矩补偿原理
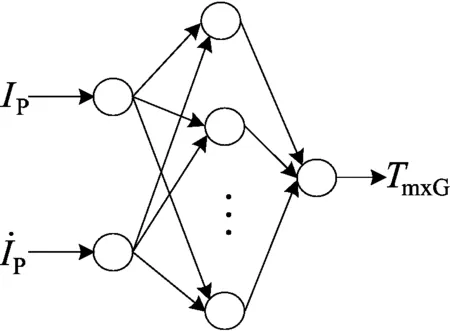
图4 BP神经网络结构
为了在现有神经网络补偿策略的基础上再进一步提高补偿精度,本文通过GA算法对BP神经网络的初始权值和阀值进行优化,最终使改进后的神经网络输出值尽量逼近目标固有摩擦力矩值,从而消除SBW系统因固有摩擦力矩不同而造成的路感差异化。
3.2.2 基于GA算法的BP神经网络模型
GA算法[13]采用概率化的自适应迭代寻优方法,在全局搜索过程中能够指导和优化搜索空间,并能自适应调整搜索方向,即使所要操作的结构对象具有无规则、不连续等特点,也能以较大概率寻找整体最优解。该算法主要是根据所选择的适度函数并结合遗传中的选择、交叉和变异对个体进行筛选,遵循自然界中的“优胜劣汰、适者生存”的生物进化原理,将适应度好的个体保留,淘汰适应度差的个体。
本文利用GA算法的全局搜索能力来优化BP神经网络的初始权值和阀值[14-15],代替BP神经网络中初始权值的随机选取,然后运用BP算法在数据空间中对网络进行精调,使最终的输出结果以接近0的误差逼近最优解。
该模型发挥了神经网络强大的非线性映射能力和GA算法全局最优搜索能力,提高了神经网络的学习速度,比单一的BP神经网络拥有更高精度的逼近能力。
经过GA算法优化的BP神经网络数学关系描述如下:
(9)
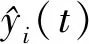
神经网络输出值表示如下:
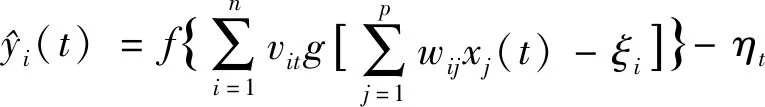
(10)
其中,f为输出神经元激励函数;vit为隐层节点到输出层节点的连接权值;g为隐层神经元的激励函数;wij为输入层节点到隐层节点的连接权值;ξi为过程神经元的输出阀值;ηt为输出神经元阀值。
检测样本平均均方误差为:
(11)
(11)式表示对神经网络输出数据准确度的估计,为满足输出数据的可靠性,q应小于一定的误差。
权值修正量表示为:
Δwij(m)=-ηg(m)+αΔwij(m-1)
(12)
其中,η为自适应学习率;g(m)为当前误差函数对权值的梯度;α为动量因子;m为迭代次数。
基于GA算法的BP神经网络设计流程如图5所示。
GA-BP神经网络建立的具体步骤为:
(1) 建立初始的BP神经网络结构,初步设定神经网络相关参数。
(2) 利用GA算法进行编码产生初始种群,通过适应度选择、交叉、变异等遗传操作获取最优权值阀值。
(3) 将这些最优权值阀值对BP神经网络进行优化,经过大量数据训练、迭代获得最佳的BP神经网络结构。
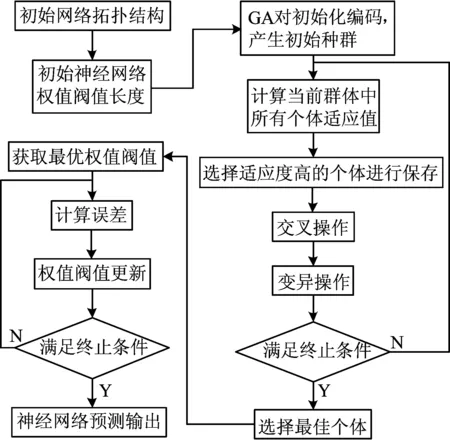
图5 基于GA算法的BP神经网络流程
4 仿真分析
为验证本文摩擦补偿策略的有效性,在Carsim中设置整车参数和行驶工况,并与Matlab/Simulink进行联合仿真。本文主要进行了中速50 km/h和高速90 km/h的双纽线仿真实验以及汽车原地转向限位试验。
仿真中选用2种转向盘总成,内部摩擦力矩设定为0.1、0.2 N·m,并分别设计了3种补偿模式进行对比,即不进行任何摩擦补偿、只添加改进型库伦摩擦补偿以及进行本文设计的摩擦补偿,仿真结果如图6所示。
由图6可知,在不进行任何摩擦补偿时,SBW系统路感与传统转向操纵力矩相比有很大差异,会导致驾驶员不能很好地适应;加入改进型库伦摩擦补偿后,相同角度上、下力矩之差明显增大,与EPS系统的转向力矩相似,但因固有摩擦力矩的不同而造成路感力矩的差异并没有消除。
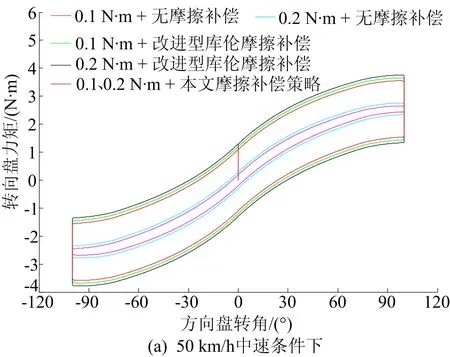
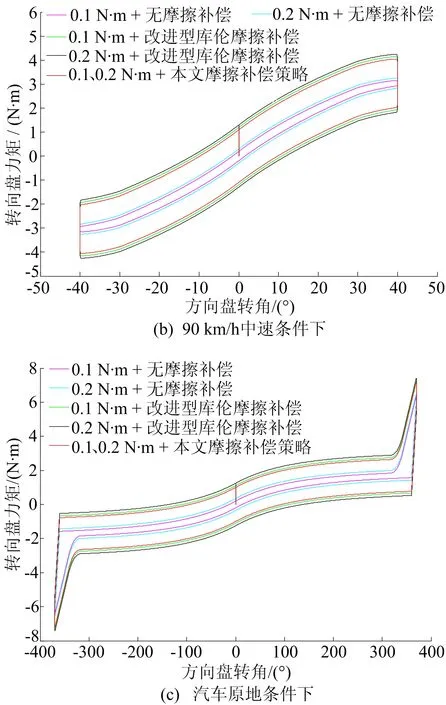
图6 3种条件下转向时转向盘力矩变化的仿真结果
从图6还可以看出,当添加本文设计的摩擦补偿后,无论是50、90 km/h还是原地条件下转向,GA-BP神经网络都可以将2套转向盘总成内部的摩擦力矩进行精确逼近,然后根据该力矩计算出补偿电流控制路感电机抵消固有摩擦力的影响,使补偿后的2个转向盘总成都呈现出相同的路感力矩,差异化得到了消除。
5 硬件在环试验
为了进一步验证本文补偿模型的有效性,搭建了SBW系统路感模拟硬件在环试验台,如图7所示。
试验台主要由转向机器人、转向盘总成、DAQ和CAN总线组成的信号采集系统、路感控制器和电源系统等构成。
从实验室中选取2个同型号的转向盘总成用于本文摩擦补偿控制策略的验证试验,其中转向盘总成分别记为A、B。在试验前先对它们内部的摩擦力矩分别进行了测量,结果如图8所示。
从图8可以看出,转向盘总成A的内部摩擦力矩在0.1~0.2 N·m之间,转向盘总成B的内部摩擦力矩在0.2~0.3 N·m 之间。

图7 SBW系统路感模拟硬件在环试验台
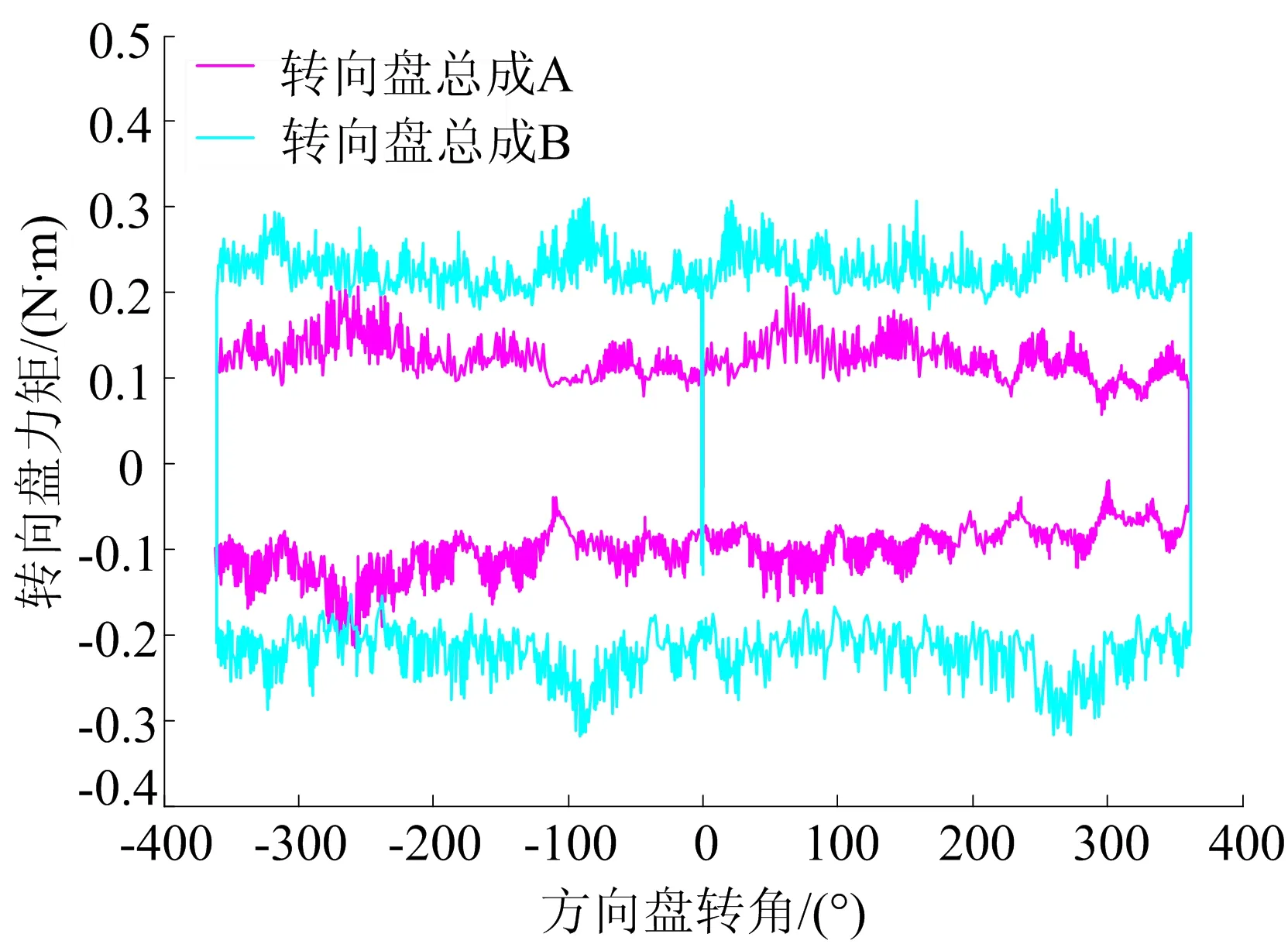
图8 转向盘总成A、B的内部摩擦力矩
硬件在环试验的工况设置与仿真中一致,用转向机器人控制转向盘转动,采集的转向盘力矩的变化情况如图9所示。由图9可知,转向盘总成A、B在无摩擦补偿时,同角度上、下力矩之差为系统内部摩擦力矩,该力矩值较小,使驾驶员在同角度向不同方向转动方向盘时手感几乎相同,与真实的驾驶感觉相差较大;加入改进型库伦摩擦之后,这种情况得到了很好改善,增强了相同角度不同转向时手感的辨识,但转向盘总成A、B之间的差异依然存在,且系统固有的摩擦力矩没有得到消除,使转矩存在较为明显的抖动。
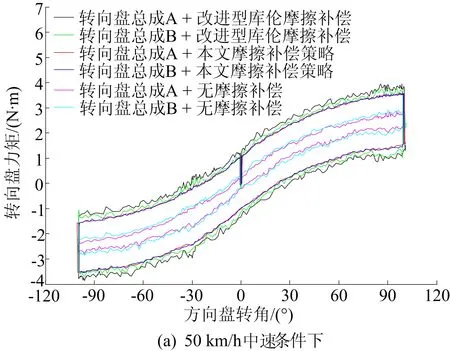
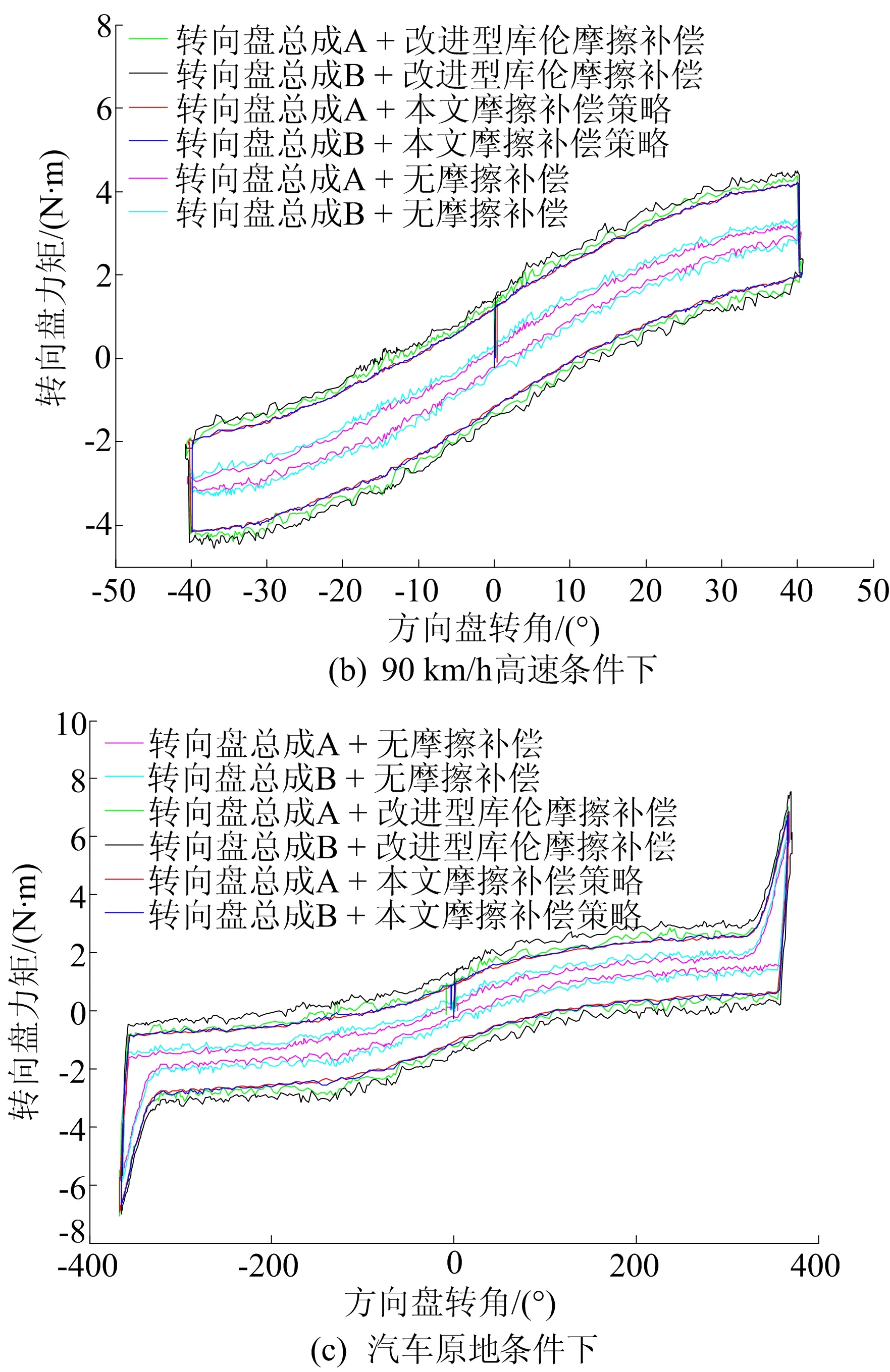
图9 3种条件下转向时转向盘力矩变化的试验结果
从图9还可以看出,本文摩擦补偿控制策略通过GA-BP神经网络对系统摩擦进行逼近和补偿,使得在不同车速条件下仍有较高的精度,使用本文摩擦补偿控制策略不仅消除了原始摩擦力矩不同造成的力矩差异,还有效地抑制了转向盘转矩的抖动。
6 结 论
(1) 本文在分析SBW系统的组成和工作原理的基础上,对转向盘力矩的组成进行了阐述与设计。
(2) 针对SBW系统在机械结构上不是相连的整体以及转动方向盘时内部摩擦力矩较小的缺点,设计了改进型库伦摩擦模型和GA-BP神经网络模型相结合的摩擦力矩补偿策略。
(3) 仿真和试验环节均选取2个不同的转向盘总成,并分别采用3种摩擦补偿策略进行对比。最终结果表明,本文设计的补偿控制策略不仅提高了转向盘转动过程中力矩的辨识度,与真实转动力矩相似,还有效地抑制了转向盘力矩的抖动,消除了因制造和装配不同而造成的力矩方面的差异。
