改进果蝇算法的爬行机器人足端轨迹规划
2020-06-19孔卫东汪彩萍
孔卫东,张 利,范 杰,汪彩萍
(1.合肥工业大学 机械工程学院,安徽 合肥 230009; 2.安徽华信电动科技股份公司,安徽 合肥 230012; 3.合肥工业大学 计算机与信息学院,安徽 合肥 230601)
0 引 言
移动机器人是机器人领域的重要分支。爬行机器人作为移动机器人的一种类型,因其结构可靠、机构灵活、构型扁平等特点被广泛应用于管道检测、防灾救援、军事探测等场合,可以提高相关人员的安全性和工作效率,具有广阔的应用前景。
爬行机器人的足端轨迹规划对其移动效率、越障能力等性能有重要影响,目前对机器人轨迹规划问题的研究方法较多。文献[1]提出混合插值的方法消除了工业机器人启停振动,使机器人运行更加平稳;文献[2]使用萤火虫算法优化了经平方和加权法将多目标问题转化为单目标问题的码垛机器人的能耗和扭矩最小优化问题;文献[3]使用遗传算法对四足步行机器人足端轨迹进行了时间与功耗优化。
果蝇优化算法(fruit fly optimiation algorithm,FOA)由文献[4]首次提出,因其具有易于理解和实现、控制参数少[5]等特点得到各界学者的青睐;然而该算法存在易于早熟、全局和局部寻优不平衡、解决多元复杂问题[6]易陷入局部最优等问题。文献[7]引入步长权重系数使FOA算法具有自适应的步长,平衡了全局和局部寻优性能;文献[8]将简洁的FOA算法与遗传算法结合,用来解决一种NP-hard问题,以缩短算法时间。
本文建立爬行机器人的轨迹规划模型,将FOA算法改进,利用改进的FOA算法对该模型进行优化,并对优化过程进行数值仿真,得到优化过程曲线和优化结果,完成轨迹规划。
1 足端轨迹规划优化问题
1.1 足端轨迹规划模型
爬行机器人的足端在移动过程中处于平地行走(倾斜行走可理解为机体倾斜的平地行走)和越障行走2种情况,平地行走可理解为障碍物高度为0的越障,因此只需解决足端越障的轨迹规划即可。
爬行机器人越障过程简图如图1所示。
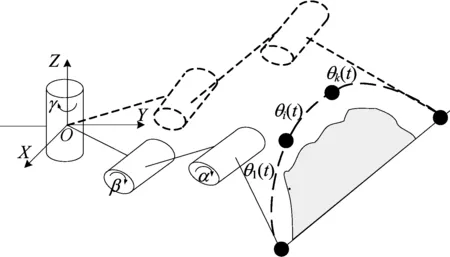
图1 爬行机器人越障过程简图
图1展示了爬行机器人一条腿越障的情况,单腿从虚线处位置向实线处位置移动,腿部共有3个关节,关节旋转角度分别用α、β、γ表示。
爬行机器人腿部各关节位移的轨迹最终表现为足端的轨迹,因此轨迹规划问题可在关节空间或任务空间中进行。在任务空间中规划需要将生成的轨迹通过逆运动学转换到各关节以控制电机完成机器人的动作,这一过程易产生奇异解,处理较为繁琐,因此本文将在关节空间中进行轨迹规划设计,即创建α(t)、β(t)、γ(t) 3个角度函数以控制最终的足端轨迹。
1.2 分段多项式轨迹规划
轨迹规划中常用高次多项式[9]进行运动拟合,通过特定的越障控制点、起终点作为边界条件计算系数。轨迹规划常用的高次多项式如下:
θ(t)=a0+a1t+a2t2+…+an-1tn-1+antn
(1)
然而该方法对路径上每个点进行求解时需要大量的计算,增大了机器人控制器的负担,而且也会造成控制的延迟,因此本文以将关节曲线通过越障控制点分成若干个低次多项式的方式,代替高次多项式来降低计算量,采用4-4-5曲线。
起点到第1个控制点及控制点之间的四次多项式为:
θn,i(t)=an,i,0+an,i,1t+an,i,2t2+an,i,3t3+an,i,4t4
(2)
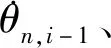
将各边界条件代入(2)式后可得系数为:
an,i,3=
an,i,4=
(3)
其中,ti为第i段轨迹的时间。
最后一个控制点和终点之间轨迹的五次多项式为:
θn,k(t)=an,k,0+an,k,1t+an,k,2t2+an,k,3t3+
an,k,4t4+an,k,5t5
(4)

各关节作用结果为图1中θk(t)。
将各控制量代入(4)式,得到各系数为:
an,k,3=
an,k,4=
an,k,5=
(5)
其中,tk为最后一段轨迹的时间。
由(3)式、(5)式可知,曲线的控制参数为各关节角度、角速度以及各段曲线的时间间隔,其中角度参数可通过越障控制点的坐标通过逆运动学计算转换到各关节得到。因此,若有k+1个控制点,则共有k个时间间隔,3k+3个角速度以及2个加速度共2k+3个控制参数代优化。
1.3 足端轨迹优化问题
本文以轨迹耗时最短为目标进行优化,优化函数为各段轨迹的时间间隔之和。运动轨迹主要受到运动学、动力学约束,每个关节的角度、角速度和关节扭矩都应在其允许范围内。
优化问题可表示如下:
(6)
其中,n为关节编号;i为分段编号。
2 问题求解算法
2.1 基本果蝇算法
FOA算法是一种群体智能演化式计算优化方法,是一种基于果蝇觅食行为推演出的寻求全局优化方法。果蝇觅食行为如图2所示。
果蝇作为一种具有优秀嗅觉和视觉能力的昆虫,在寻找食物时会首先利用其嗅觉器官嗅到食物气味,与周围果蝇进行气味信息的交流(发送或接受信息),然后得出群体中气味最好的果蝇,再利用视觉器官得到该果蝇的位置,之后群体其他果蝇均飞向该位置,并继续搜索。
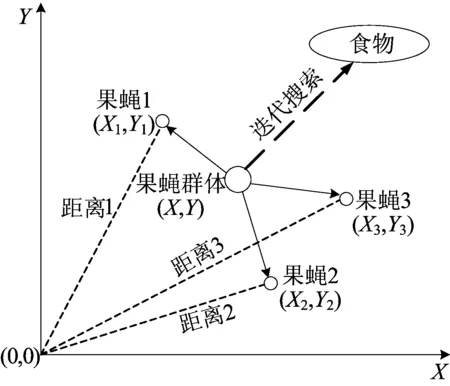
图2 果蝇觅食行为
根据果蝇觅食特点,FOA算法步骤如下:
(1) 初始化种群位置,即
Xaxis=U(m,n),
Yaxis=U(m,n)
(7)
其中,U(m,n)为m到n的均匀随机数,下文同。
(2) 赋予种群每个个体随机的飞行距离和方向,即
Xi=Xaxis+U(m,n),
Yi=Yaxis+U(m,n)
(8)
其中,i为个体编号。
(3) 由于无法得知味道来源的位置,先计算果蝇个体与原点间的距离,即
(9)
再计算味道浓度判定值,即
Ji=1/di
(10)
(4) 将每个果蝇个体的浓度判定值代入味道浓度判定函数计算味道浓度值,即
Si=fitness(Ji)
(11)
味道浓度判定函数fitness在实际问题中表示目标函数或适应度函数。
(5) 找出本次果蝇群体中味道浓度最优的果蝇浓度及其位置,即
[Sg,Xg,Yg]=min(S)
(12)
其中,g为迭代代数。
(6) 群体中其他的果蝇飞向该位置,即
Sbest=Sg
(13)
Xaxis=Xg,
Yaxis=Yg
(14)
(7) 迭代,重复步骤(2)~步骤(5),并判断味道浓度是否优于前一代味道浓度,若是则执行步骤(6),直到满足终止条件。
标准FOA算法的视觉搜索使果蝇可快速定位全局较优位置并扩散至整个种群,具有较强的全局优化能力;嗅觉搜索则提供果蝇个体在一定范围内搜索最优,具有一定的局部寻优能力。与其他群体智能算法比较,FOA的规则更为简洁、涉及的控制参数更少、更易于编程实现且计算实现时间较少。
2.2 改进的果蝇算法
虽然FOA算法在计算量、控制参数等方面有较大的优势,但也存在一些缺陷:① 不能解决负值域的最优解问题,由于(9)式、(10)式得出的解一定是正值,其适用范围具有局限性;② 较难解决极值点不在零点的问题,X、Y的值有较大的概率增加导致解Si易趋近于0并在其附近深度搜索,因此与极值在零点的问题相比,不在零点的极值优化问题较难解决;③ 在解决复杂、高维和非线性优化问题时能力较弱,根据FOA解生成规则来看,其在定义域内是不均匀分布的,即复杂问题的解空间不能被均匀地搜索;④ 易陷入局部最优[10],FOA的视觉和嗅觉操作配合可迅速找到较好的解,但当果蝇位置量较大而飞行距离较小即种群的搜索范围较小时,果蝇的搜索结果对解的影响会变得很小,使得算法陷入局部最优,易早熟。
本文的分段多项式轨迹中待优化参数较多,属于多维、复杂问题,而标准的FOA在处理复杂问题时容易陷入局部最优,主要原因是搜索半径固定以及解的生成均匀性差,因此需要对FOA进行改进。
(1) 变固定半径为自适应半径。果蝇的搜索半径影响其搜索能力,搜索半径较大则全局搜索能力强,反之则局部搜索能力强,固定的搜索半径不能很好地平衡全局与局部搜索能力,因此给予半径可变的自适应值,搜索前期半径大,可快速找到较优解,后期半径小,提高搜索解的精度。
果蝇种群初始化位置之后,随机飞行的位置为:
Xi=Xg+ωU(m,n)
(15)
ω=ω0eG
(16)
(17)
其中,ω为步长权重;ω0为初始步长权重;G为权重系数;g为当前迭代代数;Sbest为当前代历史最优浓度;Sg-1为上一代最优浓度。通过G影响果蝇个体搜索半径,G受到上一代最优浓度值和全局最优浓度值的影响,当两者距离较远时,果蝇个体离目标较远,G就较大,搜索半径就越大,果蝇个体可越快地靠近最优值,相反,搜索半径较小则进行深度搜索。
(2) 引入烟花爆炸操作。FOA因其解生成方式的局限性,具有在搜索半径变化时解搜索不均匀的缺陷,解的精度差、耗时多;而烟花算法因有特殊的爆炸机制使其可以在烟花种子附近区域搜索得均匀彻底[11-12]。利用烟花算法可以有效地改善FOA的上述缺陷。引入思路是判断2代果蝇适应度之间的变化率η的大小,即
(18)
变化率大于判定值H时采用标准FOA,反之使用烟花爆炸生成备选解,平衡算法的运算量和解的精度。
对于一次迭代产生的Si,烟花爆炸半径Ri、爆炸数目Ni的计算公式为:
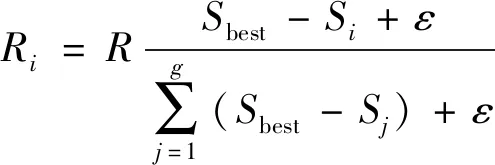
(19)
(20)
其中,Sbest、Sworst为当前历代最优、最差浓度值判定值;Si为当代浓度值判定值;R为常数调整爆炸半径大小;N为调整爆炸火花数目;ε为机器最小值,避免除零操作。
改进后的FOA伪代码如下:
1. Initialize maxgen,sizepop,R,N,Xaxis,Yaxis;
2.X=Xaxis+U(m,n),Y=Yaxis+U(m,n);
3. Caculate swarm fitnessSby Eqs.(9)-(10);
4. [Sg,Xg,Yg]=min(S);
5.Sbest=Sg;Xaxis=Xg;Yaxis=Yg;
6. Forg=1:maxgen do
7. Calculateωby Eqs.(16)-(17);
8.X=Xaxis+ωU(m,n);
9.Y=Yaxis+ωU(m,n);
10. Calculate swarm fitnessS;
11. If Eqs.(6) then
12. [Sg,Xg,Yg]=min(S);
13. Ifη<Ηthen
14. GenerateRiby Eq.(19);Niby Eq.(20);
15. Forj=1 toNido
16.l=R;Sj=Si+l;
17. End for
18. Calculate swarm fitnessSby Eq.(11);
19. End if
20. End if
21. End for
22. ReturnSbest,Xg,Yg.
3 仿真实验
3.1 仿真参数设置
对爬行机器人三自由度单腿足端轨迹进行时间最小优化仿真,仿真实验采用的软件工具是Matlab 2016。实验参数设置为:种群数量sizepop=20;进化代数maxgen=50;初始补偿权重ω0=2;烟花爆炸半径常数R=2,爆炸数目常数N=150。

表1 控制点各关节角度 (°)
3.2 仿真结果与分析
在同等条件下,使用标准FOA和改进FOA各独立运行50次时的优化统计对比结果见表2所列,2种算法的迭代优化过程曲线如图3所示。

表2 标准FOA和改进FOA 2种算法的轨迹优化统计结果
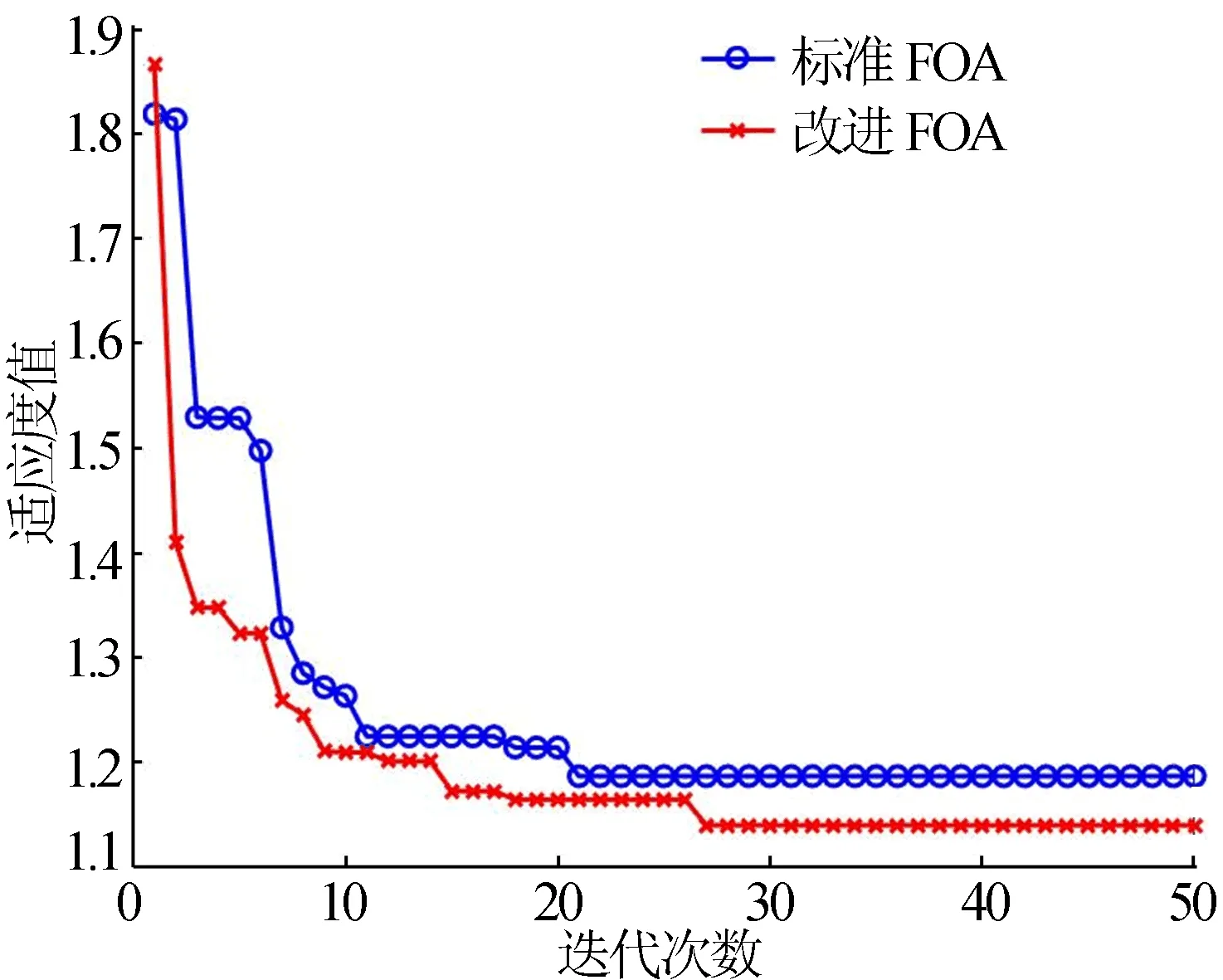
图3 标准FOA与改进FOA优化过程曲线
由表2可知,改进后的FOA能找到更优的解,同时也更加稳定,对于标准FOA易陷入局部最优和解的生成均匀性有一定的改善。
从图3可以看出,改进的FOA在迭代前期表现出较大的步长,可以更快地逼近目标最优值;而后期由于自适应的步长,步长较小,可以搜索到更精确的解,同时烟花算法的爆炸操作也令备选解的搜索更加彻底,总体来说在结果上好于标准FOA。
优化后的关节轨迹角度和角速度曲线如图4所示,篇幅有限只展示部分关节曲线。从图4可以看出,各关节的角度和角速度曲线均光滑连续,保证了关节运动的平滑,角速度的最大值也处于条件要求之内。这表明通过分段多项式进行轨迹规划是可行的,同时证明了约束条件有效,改进的FOA优化算法有效。
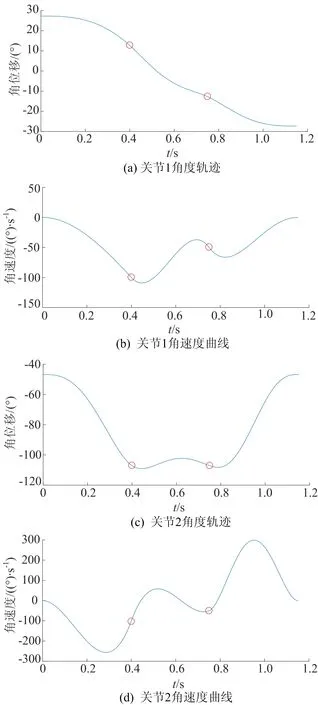
图4 关节1和关节2的角度轨迹和角速度曲线
4 结 论
本文研究了爬行机器人的足端轨迹优化问题。首先使用分段多项式设计足端轨迹,建立了以时间最优为目标的优化问题模型,并将FOA算法进行了改进,以解决该优化问题;然后结合具体算例进行了计算机仿真,仿真的结果与预期相一致。
本文改进的FOA算法提高了标准FOA算法的全局和局部寻优的平衡性以及生成解的均匀性,为爬行机器人足端轨迹规划问题提供了一种较为创新的优化方法。同时该算法也可用于其他多元复杂优化问题,只需调整相关参数以适应目标问题即可。
