基于声呐波束锐化的定向算法研究

鄢泓哲，刘玉良，毛瀚德，徐志鹏

(1.浙江海洋大学船舶与机电工程学院，浙江舟山 316022；2.国家海洋局第二海洋研究所海底科学重点实验室，浙江杭州 310012)

随着近年来国家的海洋强国战略和新式降噪舰艇的不断发展，对检测信号处理的增益处理要求越来预高，给声呐设备的检测性能增加很大压力，所以提高声呐对微弱信号的检测能力，目标参量估计能力和目标方位识别能力迫在眉睫[1-2]。目前对于如何提高声呐性能有两种方法，一种是提高基阵尺寸，这种方法虽能提高声呐方位分辨率但尺寸过大不易生产且受限于搭载平台[3-4]。另一种是信号处理方法，对于提高方位分辨率常用的有波束形成技术，基本原理是通过调整各个传感器上的时间延迟量，对于空间特定方向形成指向能力，对波束所指向的方向的信号最大化，其他方向的信号尽量抑制，也就是每次只能对一个方向形成波束[5]。根据形成的波束信号，从能量上估计出方位，从波束信号频谱上估计出的信号的特征参数。

分裂波束定向算法通过对常规算法的实用性改造，将声呐换能器基阵分为2 组，形成分裂波束算法处理，分裂波束定向算法可使主瓣尖锐、抑制旁瓣和栅瓣、降低接收端噪声级以提高对信号波达方向的估计能力，采用这种算法可以使目标分辨率接近克拉默-拉奥下界。本文将从理论分析与仿真对其在水声信号处理中进行研究。

1 常规波束形成算法

常规波束形成将一定几何形状排列的水听器输出信号经过加权处理，形成空间指向性，因此可看成一种空间滤波器，使指定方向的信号通过，滤除其他方向干扰信号[6]。而HBF 是在CBF 的基础上经过归一化运算后形成的，所以有必要对CBF 进行分析。

1.1 均匀线阵CBF

基于均匀线阵的DOA 估计可以得到待测目标的一维方向角，所以本文是在线阵基础上的分析研究。

设直线阵阵元为M 个幅度响应相同的传感器组成，待测目标相对于基阵法线的入射角度为θ，信号波长为λ，阵元间隔为d，则声呐的线阵配置图如图1 所示。

图1 均匀线阵几何形状Fig.1 Geometry of uniform linear array

则各阵元输出信号为；

由于信号到达各个阵元的时间不同，所以为了在某一方向上获得最大值需要对接收到的信号进行延迟加权处理，则相邻阵元接收信号间的相位差为：

所以常规波束形成在均匀线阵上的输出为：

1.2 常规波束形成算法仿真及结果分析

采用Matlab 进行算法仿真分析，设置32 条均匀排列的线阵，阵元间距与波长的关系为0.5，声速为1 000 m·s-1，信号频率为1 000 Hz，假定接收目标信号的方位为0°和45°。用上述CBF 算法预生成波束。

图2 0°测向角波束图Fig.2 0° beam-forming of orientation angle

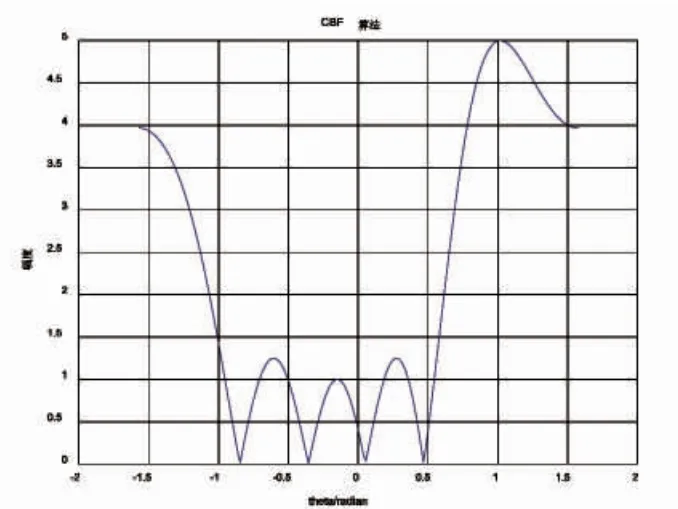
图3 45°测向角波束图Fig.3 45° beam-forming of orientation angle

从图1 的分析中可以看出CBF 算法可以在0°范围和45°范围内形成空间指向性，但主瓣宽度较宽，旁瓣级低，旁瓣幅度较大尤其在45°时旁瓣幅度几乎接近主瓣，虽然可以确定待测目标的方位，但方位角范围较大不利于精确定向。

2 分裂波束定向算法

分裂波束定向算法原理是将基阵阵元分成2 个相等的子阵。左右两个相等的子阵接收到的数据分别做波束形成处理，得到2 个波数域数据。根据2 个子阵波束形成的结果计算右子阵和左子阵之间的延时，然后对右子阵的结果进行时延补偿，然后利用互谱法分裂波束定向算法和互相关法分裂波束定向算法确定2 个子阵的细延时，然后把粗延时和细延时求和计算的到目标的精确方位[6]。

2.1 分裂波束定向算法原理

常用的分裂波束定向算法分为互谱法分裂波束定向算法和互相关法分裂波束定向算法分别从时域和频域对分裂波束定向算法进行求解。

设均匀线列阵的阵元为N，左右两个相等子阵为M 个，干扰为高斯白噪声，信号为单频平面波。M 个左子阵的输出相加得到左子阵波束数据输出，如公式(4)所示：

M 个右子阵的输出相加得到右子阵波束数据输出，如公式(5)所示：

这里要指出的是在理想情况下，所求得的t 应该是一样的但对于随机过程而言这是不可能的，只能取得最优估计值，所以要利用对小二乘法进行拟合以求出对t 的最优估计。

对各阵元信号进行傅里叶变换，得到各阵元的频域信号，则可得到左、右波束信号的频域输出为I(f)，R(f)。HBF 在左右子阵生成的左右波束I(f)，R(f)的基础上进行和运算生成和波束AS、进行差运算生成差波束AD、加权运算、系数选择形成超波束AH算法。

其中超波束指数取n[0.3 1]，总结上述流程，可得波束分裂定向算法结构如图4 所示。

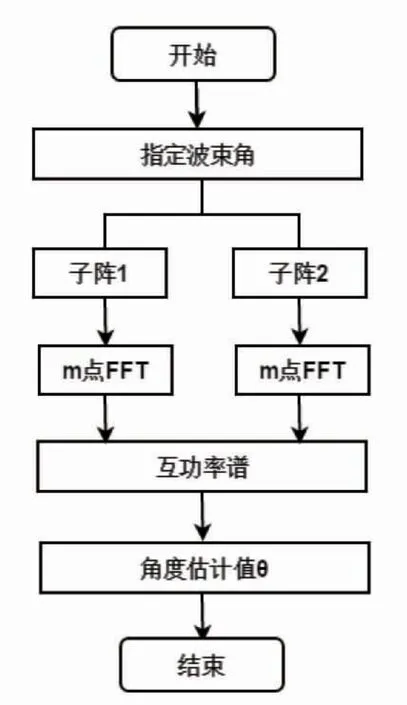
图4 HBF 算法结构图Fig.4 HBF algorithmic structural diagram

2.2 分裂波束定向算法仿真结果分析

采用Matlab 进行算法仿真分析，设置32 条均匀排列的线阵，阵元间距与波长的关系为0.5，声速为1 000 m·s-1，信号频率为1 000 Hz，假定接收目标信号的方位为0°和60°，超波束指数取5，用上述HBF 超波束锐化算法预生成波束。

通过Matlab 对CBF 算法与HBF 算法分别在目标方位为0°与45°的比较可以发现，相较于CBF 算法HBF 算法的主瓣宽度分别减小了4°与6°，旁瓣幅度明显降低，具有高旁瓣级，由此可以验证HBF确实能有效减小主瓣宽度，抑制旁瓣幅度，提高定向准确性。

图5 0°测向角波束图Fig.5 0° beam-forming of orientation angle

图6 45°测向角波束图Fig.6 45° beam-forming of orientation angle

2.3 HBF 对多目标定向研究

以上的仿真分析均是验证HBF 算法对一个目标的定向能力虽然相比CBF 主瓣宽度变窄、抑制旁瓣，但并不能说明HBF 对多个目标或相近的多个目标也具有同样的分辨率，因此有必要对多个目标进行定向方位精度仿真研究。

假设待测目标信号为3 个不同方位的窄带信号其中2 个信号为相邻信号，目标方位分别为{-60，30，35},目标信号波长为0.15，干扰噪声为高斯白噪声，声呐换能器阵元数为64，超波束指数n 为0.3，则波束仿真图如图所示。

如图所示，HBF 对多个目标仍然有很好的检测能力，在-60°，30°，35°分别检测出目标方位且主瓣较窄，旁瓣幅度较低，并且在噪声干扰下对位置相近的多个目标也具有较强的分辨力，在两目标间隔为5 时，HBF 仍然可以发现目标。通过仿真分析可以得出HBF 可以有效检测出多个相邻目标的方位。

如图8 为HBF 算法对目标俯角与仰角的估计，加入高斯白噪声，阵元数为100，方位角与仰角在0～89°范围内步长取为1 构造空间谱函数，如图所示3 个主谱峰所对应的两个坐标即使估计所得的仰角和方位角。由于HBF 算法属于波束形成算法，因而在俯-仰角联合估计中估计性能低于子空间DOA 算法，但HBF 算法作为一种波束锐化技术已经具有很强的方位估计能力。

图7 HBF 对多个目标波束形成图Fig.7 Beam-forming for multiple targets of HBF

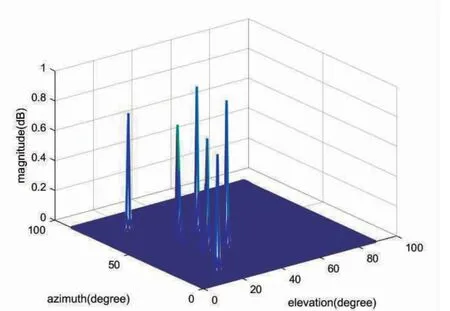
图8 HBF 对仰角与俯角联合估计Fig.8 HBF for estimation of elevation and azimuth angle

2.4 超波束指数对HBF 影响研究

由上述HBF 原理推导可知，超波束指数n 的选取对于HBF 测向分辨能力具有很大的影响，因此在实际声呐换能器设计中选取合适的n 值至关重要，通常n 的取值范围为(0～1),所以仿真参数将n 值设置为0.3，0.5 和0.7。观察在不同角度下取不同n 值对角度的影响变化。

表1 超波束指数对HBF 影响仿真结果Tab.1 Simulation results of the influence of HyperBeam index on HBF

由仿真数据结果可以看出基于HBF 测向分辨率的考虑，n 值越小定向精度越高，但n 值不能小于0.3否则性能稳定度会大大降低，实际设计研发中在不出现较大误差范围内选择合适的n 值。

3 结语

本文在分析常规波束形成算法的基础上提出了一种具有更高测向性能的分裂波束精确定向算法，并给出了该算法的分析原理与公式推导，仿真比较了常规波束形成算法与分裂波束定向算法，结果表明分裂波束定向算法具有更高的测向能力，仿真分析了HBF 对多个相邻目标的定向能力，研究了不同超波束指数对HBF 定向精度的影响给出了最优范围。但是该算法计算量偏大，需要处理的数据偏多，需要高性能的DSP 芯片处理运算，后续研究将从缩小阵元间距、扩展可处理的频率范围等方面进行深入的研究。