海底管道悬空治理数值模拟

2020-06-19单潜瑜白兴兰

浙江海洋大学学报(自然科学版) 2020年5期

单潜瑜，白兴兰

(1.浙江海洋大学港航与交通运输工程学院，浙江舟山 316022；2.浙江海洋大学船舶与机电工程学院，浙江舟山 316022；3.浙江省近海海洋工程技术重点实验室，浙江舟山 316022)

在工程设计过程中，确定悬空管道的临界长度，一般采用以下方法[1]：(1)静态强度方法：运用MOUSELLI[2]确定的管道悬跨长度与管道内静弯曲应力之间的函数关系，最大静弯曲应力不超过材料许用应力，确定许可跨长；(2)动态响应方法：将避免共振作为控制条件来计算临界跨长，即在海流作用下不发生涡激共振；(3)极限分析验算：结合以上两种分析结果，基于DNV-RP-F105 规范，以有限元法及Miner 线性累积损伤理论为依据，计算管道静应力及涡激振动引发的最大弯曲应力的合应力是否满足安全要求，确定管道悬跨长度。

国内外学者围绕海底管道悬跨临界长度的确定与悬空治理数值模拟展开大量研究。KAPURIA,et al[3]指出在进行允许悬跨长度计算时，不能忽略边界条件与轴向力的影响。安振武等[4]分析了管道的动力特性，根据涡激泄放频率小于0.7 倍的固有频率以及约化速度来确定管线的允许悬跨长度。陈博文[5]把避免共振作为控制条件，考虑了轴向应力、压强等作用，推导了不同边界条件下的允许跨长。娄敏[6]以避免涡激共振为条件推导了振动微分方程，且考虑了管内外流体作用。DNV 规范[7]中列出了以不同约化速度作为控制条件下的海底管线的最大允许悬跨长度。余建星等[8]利用涡激振动响应模型以及Miner 疲劳累积损伤准则分别从动态、疲劳筛选、疲劳损伤和极限状态四个方面对允许长度进行计算，取得了不同工况下的许可长度。付长静等[9]考虑了孤立波的作用，从管线最大静弯曲应力小于许用应力角度对允许跨长进行了推导。田晨[10]运用ABAQUS 软件从振动和强度屈服两方面确定临界跨长，并提出了安全防控措施。闫宏生等[11]针对临时管跨极限强度问题，从屈曲和屈服强度及共振强度等方面，给出计算临界跨长的方法和流程，并采用VBA 语言开发了相应计算分析软件。倪自强等[12]提出对悬跨段进行治理，采用先进的结构支撑设计手段，可以有效提高输送效率。马坤明[13]对后挖沟埋设法、结构支撑法和抛石法的优缺点进行了比较，最终选择结构支撑法。挪威Ormen Lange 项目实施中发现落石法虽能增强管道抗冲刷能力，但耗费石材[14]。导流板结构能够在一定条件下实现管道自埋和抑制管道涡激振动[15]，被墨西哥湾油田项目及北海相关的项目都有应用。国内外也用到后挖沟法，使用非接触式水力喷射挖沟机，通过高压水喷射管道底部的泥土形成管道沟渠，再利用水流作用使管道回淤填埋[16]。

基于上述研究，以舟山海域某一输气管线为研究对象，考虑管土相互作用，运用ABAQUS 软件开展动力分析，得到悬跨管线的应力状态，确定悬空的临界长度，再与基于规范和涡激振动两种方法得到的跨长结果对比，从而验证数值模型的正确性；基于临界长度，以覆盖和支撑为治理措施，进行海底管道悬空治理数值模拟与优化。

1 基本理论

1.1 屈服强度理论

长距离管道在服役状态下，受内压作用之外，还受土体、流体、地质灾害等外载荷作用，管壁上存在轴向应力、环向应力和径向应力。根据三向组合应力判断管道的屈服状态，常用的是基于von-Mises 的屈服准则，即第四强度理论：

其中：σMiese-von-Mises 屈服条件下的组合应力；［σ］为管线许用应力；φ 为安全系数，取0.9；σs为管线屈服应力。

1.2 悬跨管段振动微分方程

以某海底输气管道为例，截面为均质的环形，悬跨长为L，悬跨两侧埋设于土壤中，跨肩长度记为Lsh，计算模型如图1 所示。计算模型的基本假定如下：

图1 海底悬跨管道示意图Fig.1 Diagram of calculation for suspended span length of pipeline

(1)海床处于稳定状态而且表面平整，不出现滑坡等现象；

(2)不考虑温度、地震海啸等载荷的影响，也不考虑管道表面缺陷的影响，管道受轴力T 的作用；

(3)管内介质以速度V 匀速流动；

(4)不考虑波浪的作用，海流为稳定流，速度定为U。

管道轴线方向为X 方向，来流方向平行于Y 轴，悬空段振动位移为沿Z 向的竖向振动。

基于小变形梁的控制条件，采用Euler-Bernoulli 梁的复杂弯曲理论，忽略结构阻尼，其顺流向和竖向的运动控制方程分别表示为[17]：

其中：EI 为抗弯刚度；T 表示张力，m 为管道单位长度质量，包括管内流体质量和附加质量；y(x,t)为出平面的挠曲线(顺流向)；z(x,t)为平面内的挠曲线；Fy(x,t)、Fz(x,t)分别为单位长度管道所受海流作用的涡激拖曳力和涡激升力，可由Morison 方程[18]计算：

其中：ρ 为水密度，CM是惯性力系数，CD为拖曳力系数，CL为升力系数，Df是管道外径，Uy、Uz为流速在y、z 方向的分量。

1.3 管道固有频率计算

美国船级社提出管跨的固有频率是关于管道刚度、约束、跨度以及有效质量的函数。无阻尼自由振动时，按下式计算[19]：

若分析考虑轴向力作用下不同边界的情况，可按式(6)计算：

其中：L—管道悬空长度；C—水中取值0.7，空气中取值1.0；K—两端固定取4.73；两端简支取3.14；介于两者之间取3.92；P—有效轴向力，张力情况下为正；PE—欧拉力，两端简支为π2EI/L2，一端简支一端固定2π2EI/L2，两端固定4π2EI/L2。

2 悬跨长度确定

裸露在海床上的管道，在重力、浮力、内压、轴向力、内流以及海底环境载荷的联合作用下将出现静态和动态响应的问题[20]。管道悬空是产生涡激振动、疲劳破坏的直接原因，因此控制悬跨段长度是防止海底管道失稳的重要措施。

2.1 基于ASME B31.8 规范

根据梁复杂弯曲理论和ASME B31.8 规范，静力分析可得临界跨长[21]，计算步骤如下：

(1)计算最大纵向应力σLmax：

σLmax=0.8×Sy=288 MPa(其中：Sy为屈服强度，X52 钢取360 MPa)；

(2)根据最大许可压力计算环向应力极限σH：

σH=(Pm×D0)/2t=147.6 MPa(其中：Pm为最大许可压力，取4.3 MPa，管外径D0取508 mm，壁厚t 取7.4 mm)；

(3)泊松效应引起的轴向应力σP：

σP=-vσH=-44.278 MPa(其中：v 为泊松比)；

(4)基于最大纵向应力的弯曲应力σB1：

(5)根据von Mises 强度理论计算合应力σCmax：

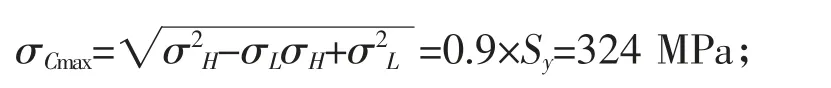
由上式可以解得考虑合应力情况下的两个纵向应力值：σL1=371.5 MPa，σL2=-223.9 MPa；

(6)最大合应力的弯曲应力σB2：

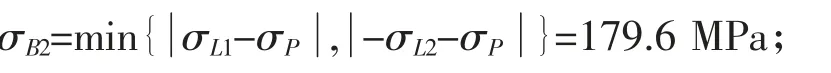
(7)最大弯曲应力σB：

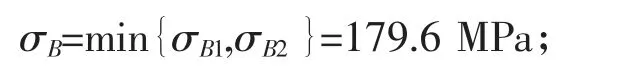
(8)最后根据弹性基础梁理论：Mmax=ZσB=qL2/10(Z 为管道抗弯截面模量；q 为作用在管道上单位长度均布荷载，取管道浸没重量)；

2.2 基于涡激振动

2.2.1 涡激泄放频率小于0.7 倍的自振频率

涡激泄放频率与管外流体速度有关，针对舟山海域实际情况，取流速U 为2 m·s-1，根据雷诺数可得斯特劳哈尔数Sr为0.2，由涡激泄放频率小于等于0.7～1.3 倍管道固有频率，可得（EI/m）1/4。

三种边界条件下分别得到临界跨长：两端固定时L=41.00 m；两端简支时L=27.22 m；一端固定一端简支时L=33.98 m。

2.2.2 约化速度小于门槛值

约化速度表示结构振动在一个周期内的流体路径与结构特征尺寸(对于管道圆柱结构尺寸为它的直径)的比值：Vr=U/fnD；判别依据

当取Vrd=4 为控制条件时，可得两端固定时L=38.65 m；两端简支时L=25.66 m；一端固定一端简支时L=32.03 m。

2.3 基于有限元法

2.3.1 管-土耦合模型

运用有限元软件ABAQUS 建模，管线模拟为S4R 壳单元，外直径508 mm，壁厚7.4 mm，管线两端为固定约束。材质选用API-X52，弹塑性参数由Ramberg-Osgood 本构关系确定。对管道两端的土体定义为实体单元，深2 m，宽10 m，土体参数根据Mohr-Coulomb 本构模型设置，埋地段管道受影响区域为一般悬跨长度的0.49 倍[22]，本文取跨长的一半。管道与土体的具体参数，见表1、表2。

表1 管道的材料属性、应力及相应塑性应变Tab.1 Physical parameters of submarine pipeline

表2 海床材料属性Tab.2 Parameters of seabed soil

悬跨管道承受的载荷包括重力、浮力、内压、温度产生的轴向力和海流力。前四步载荷采用静力通用分析步，第五步采用动力隐式分析步，设置时间为5 个周期6.35 s，最大时间增量取0.01 s。管道与土体接触部分设置接触，采用主-从面算法，管道作为主面，土体作为从面。网格数2 464，土体部分网格数总共36 744，有限元模型考虑了海床的不规则性，更接近工程实际情况，如图2 所示：

图2 管土耦合分析模型Fig.2 Coupling analysis model of the pipe-soil

2.3.2 临界悬跨长度计算结果分析

通过动态分析，得到不同悬跨长度下的最大von Mises 等效应力，其中屈服应力为360 MPa，将达到屈服应力时的悬空长度作为临界长度。悬跨管整体作为梁来分析，海床土对立管的约束作用可以模拟为铰支、固定和弹性固定端等，而实际上，管道的响应也会带来土体约束强度的降低，从而影响管道的响应。因此，悬跨管道的响应分析应考虑管-土相互作用，建立耦合分析模型。图3 表示不同边界条件的悬跨管应力随跨长的变化曲线。可知：应力随跨长增加而增加，而且随着跨长的增加，土对管道的约束作用影响越来越小，如跨长为35 m 时，3 条曲线趋向一致；对于同一跨长的管道，考虑管土耦合作用时，管道的应力较小，如跨长为15 m 时，三种情况下最大von Mises 应力分别为175 MPa、188 MPa 和211 MPa，因此，悬跨管道的跨长越短，采用简化计算方法，得到的误差将越大。基于耦合分析，将应力达到屈服强度时，对应的跨长L=30 m 作为临界跨长。

图3 不同边界条件下管道应力随跨长的变化曲线Fig.3 Variation of curves of pipe stress with span length under different boundary conditions

悬跨管的响应除了与两端边界有关以外，还有由于温度变化与内压产生的轴向力，特别是轴向压力，细长构件在压力作用下即使没有达到屈服，也会因较大位移或变形而失稳。如图4 所示，为考虑分别为轴向压力和拉力情况下，当流速为2 m·s-1时，悬跨管道的顺流向、垂直流向的位移随轴向应力的变化曲线。由图可知：(1)顺流向的位移大于垂直流向的位移，如当轴向力为零时，二者的位移分别为0.31 m 和0.24 m；(2)压力对位移的影响远大于拉力，拉力作用下可以在一定长度上减小跨中位移，此时以管道应力达到屈服作为设计条件；(3)随着轴向压力的增加，跨中两个方向的位移幅值基本上线性增加，因位移过大而失稳。因此应谨防海底管道内部产生较大的压应力。

图4 轴向力对管跨挠度的影响图Fig.4 Variation of curves of the span pipe deflection with the axial forces

3 悬空治理方法数值模拟

管道悬空治理的常用工程措施：吹泥沉降法、抛石法、支撑法、安装仿生水草、土工布联锁排覆盖等[23]，目的就是减小悬跨长度。吹泥沉降法是利用水流的冲刷作用将跨肩土体削平，从而使海管沉降，达到消除悬跨的目的；抛石法是指从船上向管道上抛填砾石等材料，填充悬空段的下方，同时压载以保证海管稳定；支撑法指的是在管道的正下方安放支撑架或填充物。常见的支撑主要有水泥沙袋、钢结构、水下灌浆袋等；安装仿生水草是通过仿生水草对海流的黏滞阻尼作用，以降低海流流速、促进泥沙淤积，解决管道悬空、淘空等问题；土工布联锁排是将混凝土小块连成一层布，覆盖在裸露的管道周围，以抵御海流的冲刷作用。

水下打钢桩作为悬跨管的支撑，水深较浅时具有较高的可靠性，如图5 所示为钢桩支撑管道的剖面示意图。基于此方法对海底管道的悬空治理方案进行结构优化的数值模拟，选择预制钢架作为支撑，通过两根桩固定在海底，其稳定性远远大于单桩，仿真整体模型如图6。管道放置在钢架下，并通过半圆形钢板(内附有橡胶胶囊防止管道损伤)进行覆盖。仿真算例管道的悬跨长度取30 m，基于管土耦合分析，建立悬跨管的数值分析模型。

图5 钢结构支撑法Fig.5 Profile sketch of steel braced frame structure

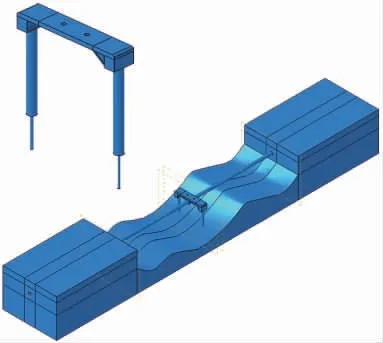
图6 钢架支撑法的数值仿真图Fig.6 Numerical simulation of steel braced frame structure

3.1 时程分析

跨中位移是影响悬跨管道失稳的重要因素，基于管土相互作用分析，研究环境载荷作用下悬跨管的动态响应，分别对治理前后的管道进行时域分析。取涡流泄放的五个周期(即6.35 s)进行观察，如图7～9 所示，治理前后的跨中位置分别为15 m 和7.5 m。可知：(1)悬跨管跨中的位移响应曲线具有稳定的周期性波动，治理前由于跨长较大，跨中的位移响应具有明显的二阶效应；(2)图7 所示的位移响应范围在75～330 mm 之间，最大幅值为255 mm，图8 的最大位移响应范围在8～20 mm 之间，最大幅值仅为12 mm，运动响应大大减小；(3)取1 个周期，对治理前后跨中位移时程曲线的对比分析，如图9 所示。可见，通过设置钢架支撑在悬跨管道的跨中，使得到管道的位移降低明显，从而增加管道的稳定性。

图7 治理前位移时程曲线Fig.7 Time history curve of displacement before suspension treatment

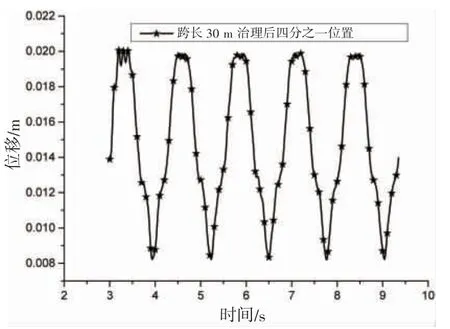
图8 治理后位移时程曲线Fig.8 Time history curve of displacement after suspension treatment

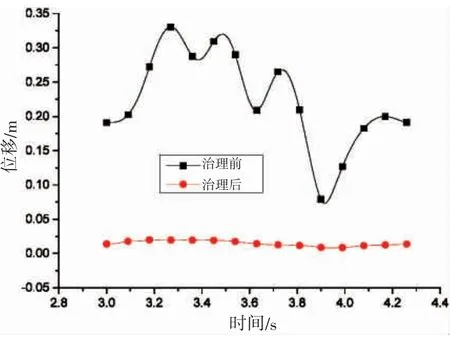
图9 治理前后位移对比图Fig.9 Comparison of time history displacement curves before and after suspension treatment

3.2 结构优化分析

3.2.1 参数敏感性分析

在管道悬跨段增加支撑以减小跨长，提高管道的稳定性，降低管道应力和位移响应，而且多跨管道的自振频率比单跨的小，可以有效避免涡激振动。为了兼顾成本与治理效果，选择结构支柱的半径、高度、宽度以及包裹长度、厚度作为参数，进行对比分析管道的位移响应和应力分析，确定优的治理方案，如图10所示为改变支撑结构时，管道的最大位移响应曲线。

图10 不同结构参数下的位移变化Fig.10 Comparison of time history displacement curves under different physical parameters

由图10 可知：(1)图a 中当支柱半径为0.1 m 时，管道跨中位移的幅值越来越大，可见支柱过于细长，不能保证支撑结构的稳定性。当半径为0.15 m、0.2 m 时，位移变化趋于稳定，二者的位移时程曲线相当接近，取支柱半径为0.15 m 时已经满足结构要求；(2)图b 为不同支柱高度下，管道跨中位移的时程曲线，位移幅值基本相同，但位移最大值随高度变化而增加，支撑高度可以根据工程实际来定；(3)图c 为包裹长度0.5 m、1 m 和1.5 m 时的位移时程曲线，三者的位移变化差异不明显，包裹长度为1.5 m 时，位移峰值相比前两者降低2 mm，包裹长度对降低管道的位移是有利的；(4)图d 和图e 为改变包裹结构的厚度和支撑的宽度，对应的位移时程曲线，比较接近，可见包裹厚度与支撑宽度的选取，符合结构自身的稳定性即可；(5)图f 为改变支撑结构横撑厚度时，跨中位移的时程变化曲线。当横撑厚度为0.05 m 时，位移曲线的波动比较明显，这也说明板太薄，结构自身稳定性较差，从而影响管道的位移响应。

3.2.2 不同治理方法对比分析

基于上节分析以及成本控制的考虑，将钢架支撑(包裹长度取1 m)和采用沙袋覆盖(覆盖长度分别取1 m，3 m，5 m)两种治理方法下，管道的位移变化曲线的对比分析。由图11 可知：采用相同覆盖长度的沙袋和钢结构，显然钢架支撑的效果更好，沙袋只有1 m 的覆盖长度时，位移响应不收敛，管道失稳。而随着沙袋覆盖长度的增大，位移响应降低。