阜阳北编组站列车到达规律分析
2020-06-19中国铁路上海局集团有限公司阜阳北站
王 平 中国铁路上海局集团有限公司阜阳北站
1 引言
阜阳北编组站地处京九铁路大通道的中段, 衔接京九、青阜、阜淮、阜漯、阜六等线路,是青阜线及漯阜线的终点,也是阜鹰汕铁路通道(阜阳—六安—鹰潭—梅州—汕头)和华东铁路二通道(阜阳—合肥—芜湖—杭州)的起点,是铁路货物运输二通道的重要节点,主要承担徐州北、郑州北、丰台西、南仓、武汉北、向塘西、乔司、芜湖东、合肥东以及蚌埠东、金华东、商丘、麻城等技术站间列车的解编任务。
阜阳北站2019 年随着三级八场扩能改造的完工,设备能力大大得到提升,“蓄水池”的作用发挥日趋明显,基本能够满足日益增长的运输需求。双向三级八场开通以来,阜阳北站日均办理辆在24 000 左右,解编日均 200 列以上,通过能力和改编能力都得到较大提升。虽也创下日办理26 542 辆的高记录,但到达场车流解不下去,外围车流接不进来的现象也经常出现。常见的是,单班当办理辆在12 000 辆左右时,班中的作业组织就很不顺畅:站内饱和站外堵车,车列移动缓慢。
在日常运输组织过程中,还会出现阶段性等线接车、车流到发不均衡调机空闲等情况;驼峰能力虚靡,调机能力浪费,站调阶段计划不兑现等情况还经常发生。
针对存在日常运输组织中存在的问题,本文将对编组站到达列车规律进行理论研究,为下一步各系统协调能力研究提供理论基础。
2 随机抽样与数据特征值计算
将阜阳北编组站列作排队的服务系统,每一列到站列车为它的顾客。顾客到达间隔时间随机性以不同的数据显示出来,列车到达间隔是一个总体,每个到达间隔是一个个体。
列车到达的间隔时间为连续型随机变数,只能随机抽取一部分的数据进行统计分析。在抽取数据时,应保证所抽取的数据是正常情况下具有一定代表性和相对独立性的数据。本文选取的是6 月1 号至6 月7 号阜阳北站列车到达间隔时间的数据。
首先应该确定数据的分组数目,数据分组数决定于数据的多少。正常来说,组数应选取10 组左右,数据的总数越大,则组数相应分的应该越多。表1 为数据分组的参考值。

表1 数据分组参考值
组距可由公式(1)确定:

其中:tmax、tmin表示的是最大和最小的时间间隔。
根据统计,tmax=135 min,tmin=0 min,考虑到分组在20 组以内,因此每组的时间要大于6 min,方便计算,把每组的时间定为7 min,因此得到△=135/7>19 组,实际取19 组,从而求出到达时间间隔的数字特征。具体情况见表2。

表2 阜阳北站列车到达时间间隔数据整理
所谓“任务驱动”,就是在学习专业技术的过程中,学生在教师的帮助下,紧紧围绕一个共同的任务活动中心,在强烈的问题动机的驱动下,通过对学习资源的积极主动应用,进行自主探索和互动协作的学习,并在完成既定任务的同时,引导学生产生一种学习实践活动。这种教学方法特别适用于学生学习操作类的知识和技能,尤其适于学习工程机械驾驶与维修方面的知识和技能。因此,“任务驱动”教学法在铁道工程机械系统故障排除课程教学中已得到运用,就笔者的教学实践来看,要有效地实施任务驱动教学,应注重以下几个方面。
均方差:σ=13.05 min;
方差是描述随机变量分散程度的定量指标,方差越大,表明随机变量与样本平均数之间差别越大。通过研究资料看出阜阳北编组站到达场列车到达的时间间隔变异系数通常在0.75~.9 之间,该数值越大,列车到达将越不均衡。
3 分布函数假设与拟合检验
3.1 分布函数假设
对连续分布的随机变量理论的分布形式假设,一般釆用直方图法。直方图法是通过观测数据值绘制成的相对应的密度函数基本图形估计,由此来进行初步判断总体理论的分布形式,这是一种简易可行的方法。阜阳北站到达间隔时间频率分布图如图1 所示。
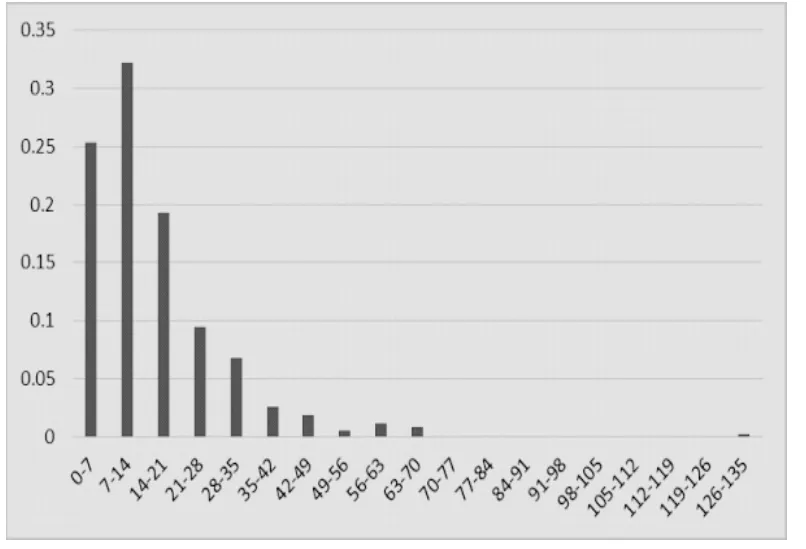
图1 阜阳北站到达间隔直方图
通过观察直方图(横坐标为列车到达间隔的时间,纵坐标为到达频率),可以判断出图形跟二阶混合爱尔郎分布密度函数的图形极为相似,由此假设列车到达时间间隔服从二阶爱尔郎分布,然后对其进行验证。
3.2 拟合检验
分布函数拟合检验方法在数理统计学中有很多,一般采用的是χ2检验法,他的基本思想是把统计的数据分成k 个独立组,将假设的理论分布计算出理论频数,再用它和统计频数相比较。通常来说,如果假设是真,其差异将不显著;如果假设是假,其差异就显著。这种检验统计量为:

其中:f*i—第i 组统计频数
Pi—第i 组的理论频率
NPi—第i 组的理论频数
k—经过并组后组数
由皮尔逊定理,各组的f*i和NPi均不小于5,否则进行并组,并且N 要大于50。若统计数据服从假设分布,则χ2将服从自由度为(K-r-1)的 χ2分布,即:
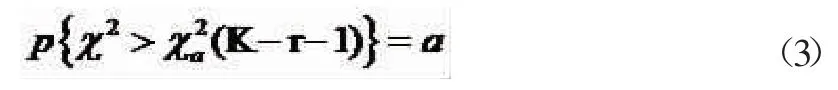
其中,r是通过统计分布求出的理论分布参数个数,α是显著水平,可以取0.05。
由于变异系数为0.84,因此他的间隔时间可以用二阶混合爱尔朗分布进行拟合。其二阶混合爱尔朗分布的分布密度函数为:

带入λ=3.9,ν=0.84,最终得到间隔时间的密度函数为:
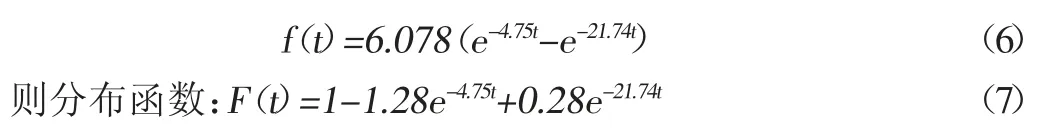
通过上述公式的计算,将所得的数据带入χ2检验的计算表中,得到表3。
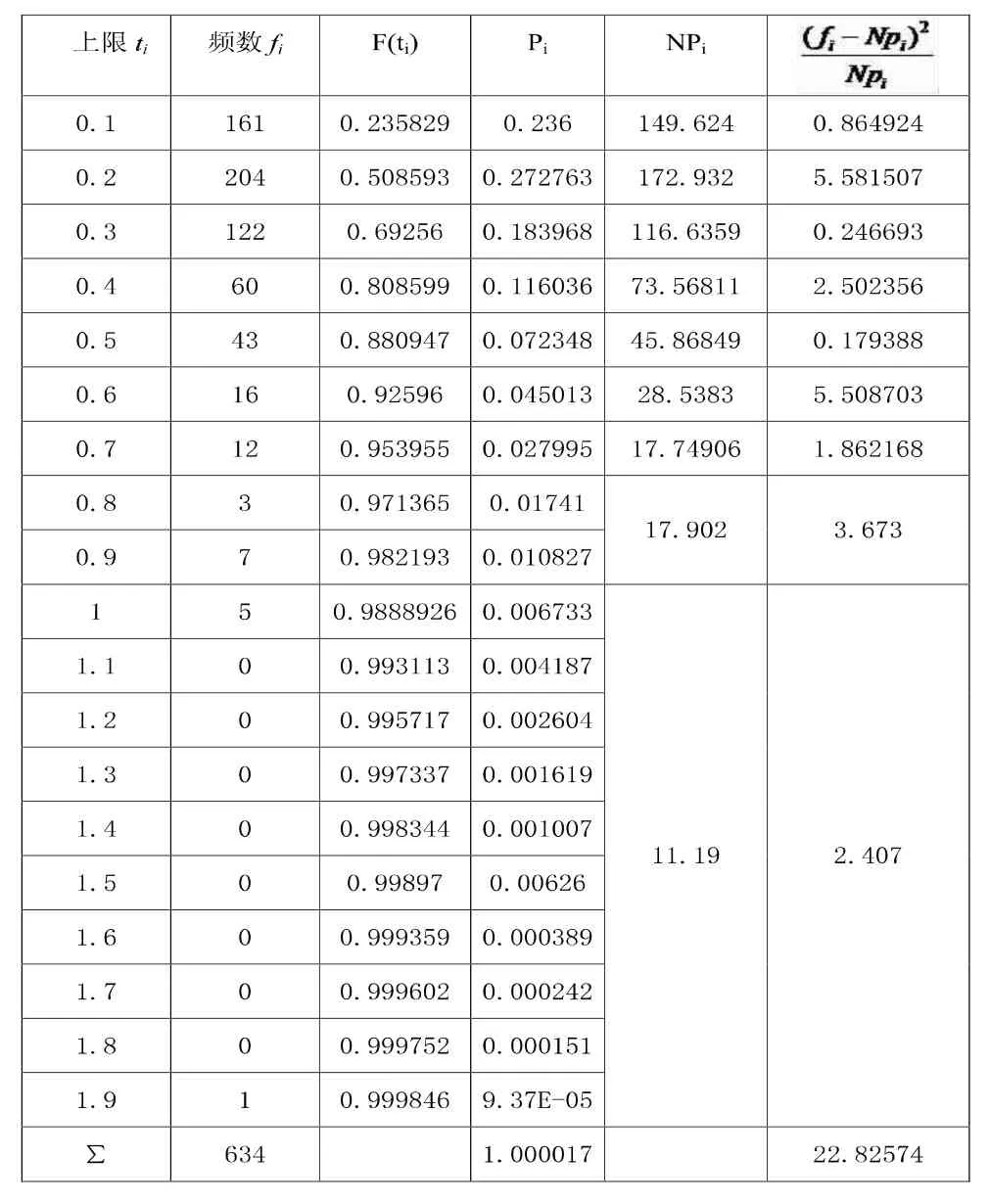
表3 阜阳北站到达系统χ2 检验计算表
由表3 可得到最终统计量χ2=22.83,经查表得到χ20.05(19-2-1)=26.296。通过上述可以判断,阜阳北列车的到达间隔时间与二阶混合爱尔朗分布相吻合。
虽然由于列车到达的不均衡程度、每列车编成的车辆数、车辆的技术状态和编组要求等因素的不一定相同,给输入流的到达时间间隔和各子系统的服务时间增添了许多随机性,但是它们在一定的具体条件下呈现出一定的分布规律,通过本文系统研究,得出阜阳北列车到达的间隔时间,服从二阶混合爱尔朗分布,对下一步各系统能力协调分析提供理论研究。
对于铁路编组站,不均衡运输主要表现为编组站货物列车到发时刻分布不均匀。这种时空的波动性,造成货物列车在不同时段相对集中到达或出发,不仅区间通过能力利用不均衡,还会导致编组站阶段性能力紧张,列车中转时间延长。
4 结束语
铁路编组站是一个大系统,由多个作业子系统组成。系统的整个协调性将是衡量各个子系统之间、系统与各外部环境之间协调关系的指标。车站能力的协调性指对车站设备系统各作业环节间协调性的度量。
研究铁路编组站协调性问题不但有利于提高运输设备的利用效率,而且为运输设备规划和设计提供了优化参数,将铁路建设相关资源得到了合理配置。
