MGF模型和SVM回归法在甘河加格达奇站年最大流量长期预报中的应用
2020-06-19刘文斌于成刚
刘文斌 于成刚
(1.黑龙江省水文水资源中心,黑龙江 哈尔滨 150001;2.大兴安岭水文水资源中心,黑龙江 加格达奇 165000)
分析预测年最大流量的主要意义在于定量描述预测年份的洪水量级,为防洪决策提供支撑,但年最大流量的变化受江河前期底水,预见期内降水、蒸发、气温,水利工程、人类活动等诸多因素影响,具有很大不确定性。常用的时间系列分析技术和预测方法(如:多元线性回归),对系列数据的极值和趋势预测,不能体现年最大流量因受大气环流变化而具有的与预报因子之间的非线性关系,存在精度不高的问题。现有的时间序列预测模型中,自回归(AR)、自回归滑动(ARMA)和门限自回归(TAR)模型在进行多步预测时,预测值会趋于平均值,对极值的拟合效果欠佳。指数平滑模型和灰色模型等进行多步预测时,表示的是一种指数增长,不适用于预测起伏变化大的年最大流量。
针对时间系列预测模型对于转折性变化预测能力较差的问题,依据气候时间序列蕴涵不同时间尺度振荡的特征,魏凤英[1]拓展了数理统计中算术平均值的概念,定义了时间序列的均生函数,提出了视均生函数为原序列生成的、体现各种长度周期性的基函数的新构思。均生函数预测模型既可以作多步预测,又可较好地预测极值,为长期预报和短期气候预测开辟了一条新途径[3]。采用均生函数作多步预测,可以改善其他时间序列模型的不足,改善对序列极值的拟合与预测效果。
支持向量机(Support Vector Machines,SVM)以统计理论为基础,能较好地解决小样本、非线性、高维数和局部极小点等问题,是一种新颖有效的处理非线性分类和回归的方法。本文即以均生函数构成的周期性函数,结合支持向量机方法建立了甘河的加格达奇站年最大流量预测模型,有机地结合两种方法的优点,克服了传统时间系列预测方法对极值模拟精度较低和长期预测中存在的趋势性预测的问题。在加格达奇站年最大流量预测的应用结果显示,本文建立的模型预测结果既实现了数量和趋势同步预测,也实现了该年最大流量系列非线性变化的预测,大大提高了预报精度。
1 研究资料和方法
1.1 资料
甘河发源于大兴安岭东坡伊勒呼里阿仑山脉的南支英吉奇山,由西北流向东南,汇入嫩江干流,全长446km,流域面积19549km2,流域内森林覆盖率高,没有过多人为活动影响,下垫面条件变化不大。加格达奇水文站为甘河中游控制站,多年平均降水量531mm,年际变化大,年内分布主要集中在6—9月,该站洪水为典型山溪性洪水,暴涨暴落,涨水期间水位、流量变化剧烈。
本文所用的资料为加格达奇站1952—2019年共68年的年内最大流量序列资料。
1.2 均生函数模型
均生函数(Mean Generating Function,MGF)是时间序列均值生成函数的简称,是由时间序列按不同时间间隔计算均值,生成的一组周期函数[7],将此函数进行周期性延拓,即在定义域上延拓到整个数轴,可构造出均生函数延拓矩阵。魏凤英[1]将均生函数的概念推广到回归分析中,给出相应的建模方案,使回归模型的拟合效果更为理想。
利用加格达奇站年最大流量系列构造最大流量周期性均生函数,采用CSC[1]双向评分准则,选择最优因子,利用SVM的K-CV统计分析方法学习训练样本,通过逐渐改变参数的取值,获取最佳的参数组合,而后建立回归模型进行拟合。计算1952—2001年的拟合值。根据模型对2002—2019年最大流量进行预测,最后与2002—2019年实测资料进行对比分析。
设时间序列为X(t)(t=1,2,…,n),构造均生函数:
(1)
(2)

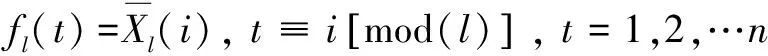
(mod表示同余)
(3)
F=(fij)n×m,fij=fl(t)
(4)
(5)
fl(t)为均生函数延拓序列,是一种周期性基函数。均生函数延拓矩阵中第1列记为f1,第2列记为f2,……,第m列记为fm。从f1、f2、…、fm中挑选出m个与原始序列密切相关的序列作为预报因子,建立模型进行模拟和预测。
1.3 支持向量机(SupportVector,SVM)回归方法
支持向量机(SupportVector,SVM)是一种基于统计理论的算法,属于有监督的学习方法,已知训练点的类别,可学习求得训练点和类别之间的对应关系,以便将训练集按照类别分开,或者预测新的训练点所对应的类别。
用线性回归函数f(x)=ωx+b拟合数据{xi,yi},(i=1,2,…,n,xi∈Rd),yi∈R的问题,根据SVM理论,若采用线性ε不敏感损失函数
(6)

(7)
下,最小化目标函数
(8)
常数c>0控制对超出误差ε的样本的惩罚程度。采用优化方法可以得到其对偶问题,即在约束条件
(9)
(10)
从而得回归模型
(11)

(12)
式(5)、(6)中的b*,取在边界上的一点,即可确定。有关非线性核函数的种类较多,常用的有多项式核函数、径向基核函数、柯西核函数等多种形式。本文采用径向基核函数
K(x,xj)=exp(-(γ‖x-xi‖2),λ>0)(13)
1.4 年最大流量延拓均生函数
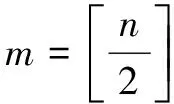
选取通过置信度0.01~0.05检验的函数因子作为预报因子。所选取的周期性基函数因子为5个。这5个周期性基函数分别为5年、11年、16年、18年、19年的函数,其中11年、18年的基函数因子通过了0.01的检验。这样有效避免函数因子之间的复相关,确保各个因子间的独立性。
2 周期检验和突变检验
2.1 周期检验
周期性检验采用小波分析法,该方法最早提出于20世纪80年代初,具有时-频多分辨功能,能清晰地揭示出隐藏在时间序列中的多种变化周期。本文计算所用年最大流量系列包含“多时间尺度”变化特征且这种变化是连续的,所以选用连续复小波变换来分析该流量序列的多时间尺度特征,结果见图1,结果显示该系列存在11年、34年左右明显的周期。
因此,加格达奇站流量随时间出现周期性变化,具有一定起伏性,适合用MGF和SVM来解决极值预报的问题。
2.2 突变检验
流量系列的突变检验,采用滑动t检验(MMT)的方法。两子系列长度n1=n2=11。给定显著性水平a=0.01,t分布自由度ν=n1+n2-2=20,t0.01=±2.85,为了提高更严格的显著水平,给定t0.01=±3.20。将计算出的t统计量序列和t0.01=±3.20绘成图2。图2显示,流量系列自1952年以来,t统计量有一处超过0.01显著水平,且为正值,说明年最大流量在20世纪70年代经历了一次由大到小的突变。该次突变包含在过去的变化中,后期系列未出现突变,因此,可以依据率定的模型进行多步预测。
3 年最大流量预测模型
3.1 SVM回归预测模型的建立
为了避免挑选出的周期性基函数因子之间的量级差异,消除各个因子由于量纲和单位不同造成的影响,首先对每个预报因子进行归一化处理:
(14)
式中:xmax、xmin为原始数据x的最大值和最小值;ymax、ymin为映射范围的参数,在这里取值为2和1。

图3 加格达奇站年最大流量归一化后逐年数据曲线
建模时,将经过处理的预测因子(优选后的周期性基函数)作为输入,年最大实测洪峰流量作为输出,取前50年(1952—2001年)为检验样本集,用于SVM进行学习训练和验证,后18年(2002—2019年)为预测检验样本,归一化后逐年数据曲线见图3。选取线性ξ不敏感损失函数,采用径向基核函数进行SVM建模,由于所选的参数值不同,函数形态会发生较大变化,进而引起SVM模型的变化。因此,在建模中利用K-CV[8]统计分析方法学习训练样本,通过逐渐改变参数的取值,以获取最佳的参数组合,使建立的模型预测效果最好。经过多次交叉验证学习和训练,最终建立用于年最大洪峰流量预报的SVM回归模型,经过计算其校正模型参数c为11.31,g为0.35,MSE为0.013。其参数计算结果见图4、图5。
3.2 SVM回归模型预测效果分析
依据《水文情报预报规范》(GB/T 22482—2008)对中长期预报的精度评定的要求,流量数值预报误差精度采用多年变幅的10%,而趋势(定性)评分采用合格和不合格[4]。
SVM模型模拟和检验结果显示:模拟和检验效果较好,精度较高,50个模拟数据符合误差要求的共42个,合格率达84.0%;46个数据趋势模拟正确,合格率达到92.0%。18个检验数据符合误差要求的共13个,合格率为72.2%;14个数据趋势模拟正确,合格率达到77.8%。极值的模拟结果较好,模拟数据的极值数据均符合误差要求,预测值和实际观测值对比曲线见图6。
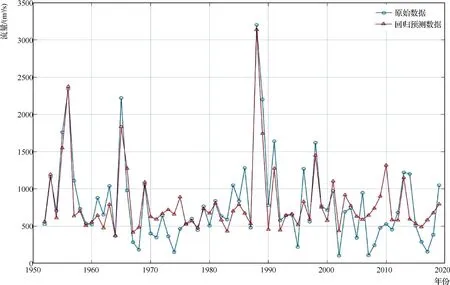
图6 加格达奇年最大流量SVM预测值和实际观测值对比曲线
3.3 逐步回归预测模型
为了比较SVM回归与逐步回归方法的预测能力,本文同样利用上述19个周期性基函数作为预报因子,选取不同F值引入不同的预报因子,采用逐步回归方法建立加格达奇站年最大流量预测模型。依据模型的预测误差最小原则,数学方程为
+0.547x19-1889.905
(15)
对检验样本和预测样本年最大流量数据进行了预测模拟,其回归结果和实际观测值对比见图7。
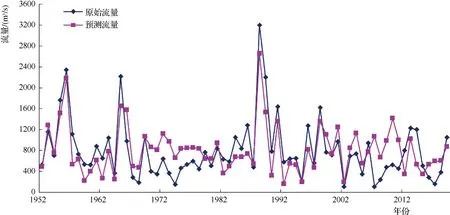
图7 加格达奇站年最大洪峰流量多元逐步回归预测值和实际观测值对比曲线
3.4 逐步回归模型预测效果分析
采用上述预报误差精度进行评定,模拟和检验效果都不好,50个模拟数据符合误差要求的共30个,合格率为60.0%;44个数据趋势模拟正确,合格率达到88.0%。18个检验数据符合误差要求的共10个,合格率为55.6%;9个数据趋势模拟正确,合格率为50.0%。极值的模拟结果也不好,从图7可以看出有2个极值的模拟数据差距都很大。
3.5 两种模型对比分析结果
根据两种方法的模拟结果,逐步回归模型的数值预测合格率为60.0%,SVM回归方法构建的模型合格率为84.0%,两者相差达到24.0%。趋势上逐步回归模型合格率为88.0%,SVM方法构建的回归模型合格率达到92.0%,两者相差4.0%,但是逐步回归在2个极值的模拟上都出现了较大差距,而SVM方法构建的回归模型3个极值都模拟预测的很好。18年的检验结果中,逐步回归模型的数值预测合格率为55.6%,趋势模拟合格率为50.0%,而SVM回归方法构建的模型合格率为72.2%;趋势模拟合格率达到78.8%。
4 结 论
a.通过对加格达奇站年最大流量系列进行小波分析和滑动t检验,发现数据系列存在11年、34年左右周期,而在20世纪70年代存在一个由高到低的突变,说明该系列存在着明显的非线性变化。按常规长期预报方法需提取周期、滤波趋势,以及构建随机过程的模型来进行外延预报。但如前文所述,常规预报方法并不能较好处理非线性数据系列,对极值和趋势变化的预测能力尚有改善空间。本文即采用均生函数(MGF)、支持向量机(SVM)相组合的方法来提高预测能力。分析预报结果显示,无论是极值还是趋势预报,合格率均较高。
b.采用均生函数 (MGF)构建时间序列的周期性基函数,并对均生矩阵进行周期外延得到延拓矩阵,有效地实现了对时间系列数据的重构,一定程度上避免了单数据系列对预报结果的负面影响;而因子选取上采用CSC双评分准则,提高了模型在数据趋势预测上的能力,从而实现了数量和趋势的双预测。
c.运用SVM方法中的K-CV统计分析方法学习训练样本并优化参数。经过多次交叉验证学习和训练,最终计算其校正模型参数c为1,g为0.353,MSE为0.0081。交叉验证提高了SVM类别识别最优参数集,间接提高了SVM回归模型的精度。
d.通过均生函数(MGF)生成30个周期性基函数,采用CSC双评分准则,筛选部分周期性基函数作为预测对象的影响因子,运用SVM中的K-CV统计分析方法学习训练样本、优化参数,最终建立年最大流量预测模型。模型预测结果显示,无论模拟还是检验,本文所构建的模型均表现出明显优势,尤其在趋势和极值的预测上克服了AR、ARMA等时间预测模型的极值均值化的问题。
e.对比采用均生函数(MGF)、多元逐步回归相组合传统预测方法,本文所构建模型的预测结果无论是极值还是趋势预测都远远优于传统预测方法,尤其在系列极值的预测能力上表现更为明显。结果表明,新构建模型在处理年最大流量非线性变化方面有一定程度的改善。
根据目前水文行业开展年最大流量预报的实际情况,传统中长期预报方法存在细节处理不细致、预测精度有待提高等问题,尤其针对极端洪水或干旱年份,极值预报误差较大。本文主要针对数据系列的非线性变化和存在极值问题,利用均生函数(MGF)并结合支持向量机(SVM)构建年最大流量预测模型。通过在甘河加格达奇站的实际应用并与逐步回归预测方法对比,本文所构建模型在模拟和检验中的预报结果均呈现明显优势,应用于工作实际是可行的。从水文领域的应用来看,该模型不仅提高了年最大流量非线性及极值预报能力,也实现了数量和趋势双预报,可更好应用于中长期预报。
