温度影响下变截面梁自由振动与屈曲的微分变换法求解

2020-06-18林鹏程王俊淋滕兆春

甘肃科学学报 2020年3期

林鹏程,王俊淋,滕兆春

(兰州理工大学理学院,甘肃兰州 730050)

变截面梁广泛应用于工程实践中,例如建筑中的钢结构和飞行器内部骨架的梁和墙。为了适应结构内力变化和结构外形的需要,将支承附近的梁高加大,而靠近跨中的梁高则取得较小,从而形成变高度梁[1],即变截面梁。考虑到变截面梁工作的特殊环境,研究其在热载荷作用下的力学响应具有实际的工程应用价值。目前已有一些关于变截面梁的力学行为研究成果[2-7]。变截面梁振动问题中,控制微分方程的求解通常很困难,得到解析解则更艰难,采用一般的数值解法有复杂繁琐的公式推导过程,也不容易求解。微分变换法(DTM,differential transform method)能将线性或非线性微分方程转换为代数方程求解,是一种非常实用并有重要价值的求解方法[8]。已有很多学者发现了DTM的求解方便、结果准确的特点,并应用于结构的静力学和动力学分析中[9-11]。

目前,用DTM分析变截面梁在温度影响下的自由振动与屈曲在国内外还未见有文献报道,因此研究采用DTM对在温度影响下的变截面梁的自由振动与屈曲问题进行分析。首先建立温度影响下变截面梁的力学模型,基于Euler-Bernoulli梁理论推导变截面梁在温度影响下的自由振动控制微分方程并进行无量纲化;其次对控制微分方程以及边界条件进行微分变换;最后分析了截面变化系数和无量纲升温对变截面梁自由振动频率的影响,并求解了不同截面变化系数情况下变截面梁达到屈曲状态时的临界温度。

1 控制微分方程及参数的无量纲化

图1中考虑两端不可移约束情况下受温度载荷作用的矩形变截面梁并建立笛卡尔直角坐标系。变截面梁的长度为l,宽度为b。假设梁的高度按线性

图1 热环境中变截面梁模型

变化,其热膨胀系数为α,弹性模量为E。

根据热应力理论[12],在没有约束的情况下,梁在热环境中的自由伸长量Δl为

Δl=αΔTl,

(1)

其中:ΔT=T-T0为温度变化;T为当前温度;T0为初始温度。

距梁左端x处的梁高度为

(2)

其中:h0为梁左端的初始高度;β称为截面变化系数。距梁左端x处的梁的横截面积为

(3)

距梁左端x处由于热应力引起的线应变为

(4)

其中:NT为温度载荷作用下变截面梁的热轴力,热轴力NT引起梁上一微段的伸长量Δl′为

(5)

该微端在x方向被完全约束,使得自由热膨胀伸长量和由热轴力NT引起的伸长量的总变形量为0,由此可得由于温度变化所引起变截面梁的热轴力为

(6)

利用Euler-Bernoulli梁理论,忽略横向振动中剪切变形和截面绕中性轴转动惯量的影响,由梁上微段的平衡关系和挠曲线近似微分方程得到温度影响下变截面梁自由振动的微分方程为

(7)

其中:ρ为梁的质量密度;t为时间。

对于梁的简谐振动,可令

(8)

(9)

其中:τ为无量纲升温;Ω为无量纲频率。

将式(8)和式(9)代入式(7)中,得到温度影响下变截面梁自由振动的无量纲控制微分方程为

(1+βξ)Ω4W(ξ)=0。

(10)

温度影响下变截面梁的自由振动与屈曲问题只考虑工程应用中最实际的夹紧(clamped)和不可移简支(simply supported)情况,则边界条件的无量纲形式为:

ξ=0处:

(11)

(12)

ξ=1处:

(13)

(14)

2 无量纲控制微分方程及其边界条件的DTM变换

DTM是一种有效的半解析解法,基于Taylor级数展开进而求解微分方程。运用DTM对变截面梁在热载荷作用下的临界温度特性问题进行求解时,首先需要将其无量纲控制微分方程和边界条件经DTM变换为相应的由离散函数组成的代数方程。

根据函数的Taylor公式,经过DTM变换后的函数F[k]定义[8]为

(15)

F[k]的逆变换为

(16)

由式(16)、式(17)可得

(17)

在实际应用中,f(x)采用有限多项式求和,式(17)可改写为

(18)

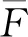
(19)

其中:

B0=(k+1)(k+2)(k+3)(k+4),

B1=(3βk+6β)(k+1)(k+2)(k+3),

(k+1)(k+2),

B3=[(k-1)(k-2)β3k+6β3k(k-1)+

6β3k)](k+1),

B4=-Ω4,

B5=-βΩ4。

式(11)～式(14)边界条件经DTM变换后为:

ξ=0处:

(20)

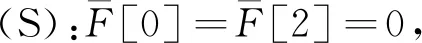
(21)

ξ=1处:

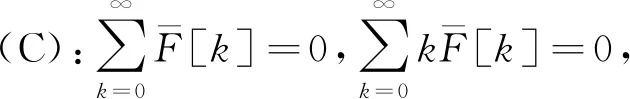
(22)

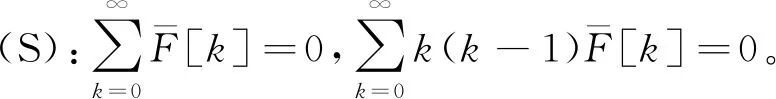
(23)

3 计算结果和分析

通过编写计算软件程序可获得式(19)在边界条件式(20)～式(23)下的无量纲固有频率。为了验证计算模型的准确性及DTM求解方法的有效性,表1给出了β=0和τ=0时,将原问题控制微分方程退化为等截面梁和无温度影响作用时的前3阶无量纲固有频率采用DTM的计算结果,并与文献[13]的解析解做了比较。从表1可看出研究结果与文献[13]的结果完全吻合,说明DTM对求解此问题有效可靠。

表1 等截面梁的无量纲固有频率比较 (β=0,τ=0)

图2给出了截面变化系数β=0.4时,C-C、C-S和S-S 3种不同边界条件下的变截面梁的1阶无量纲固有频率随无量纲升温τ变化的关系。由图2可见,3种边界条件下的1阶无量纲频率都随无量纲升温τ的增大而减小,当无量纲升温趋近于临界温度时,1阶无量纲频率急剧减小,很快达到屈曲状态。这是由于梁失稳时的振动具有无限大的振动周期,其固有频率应为0。故式(19)中若取Ω=0,则可得到计算变截面梁各阶热屈曲模态温度升高值的控制微分方程,其最小值即热屈曲临界温度。

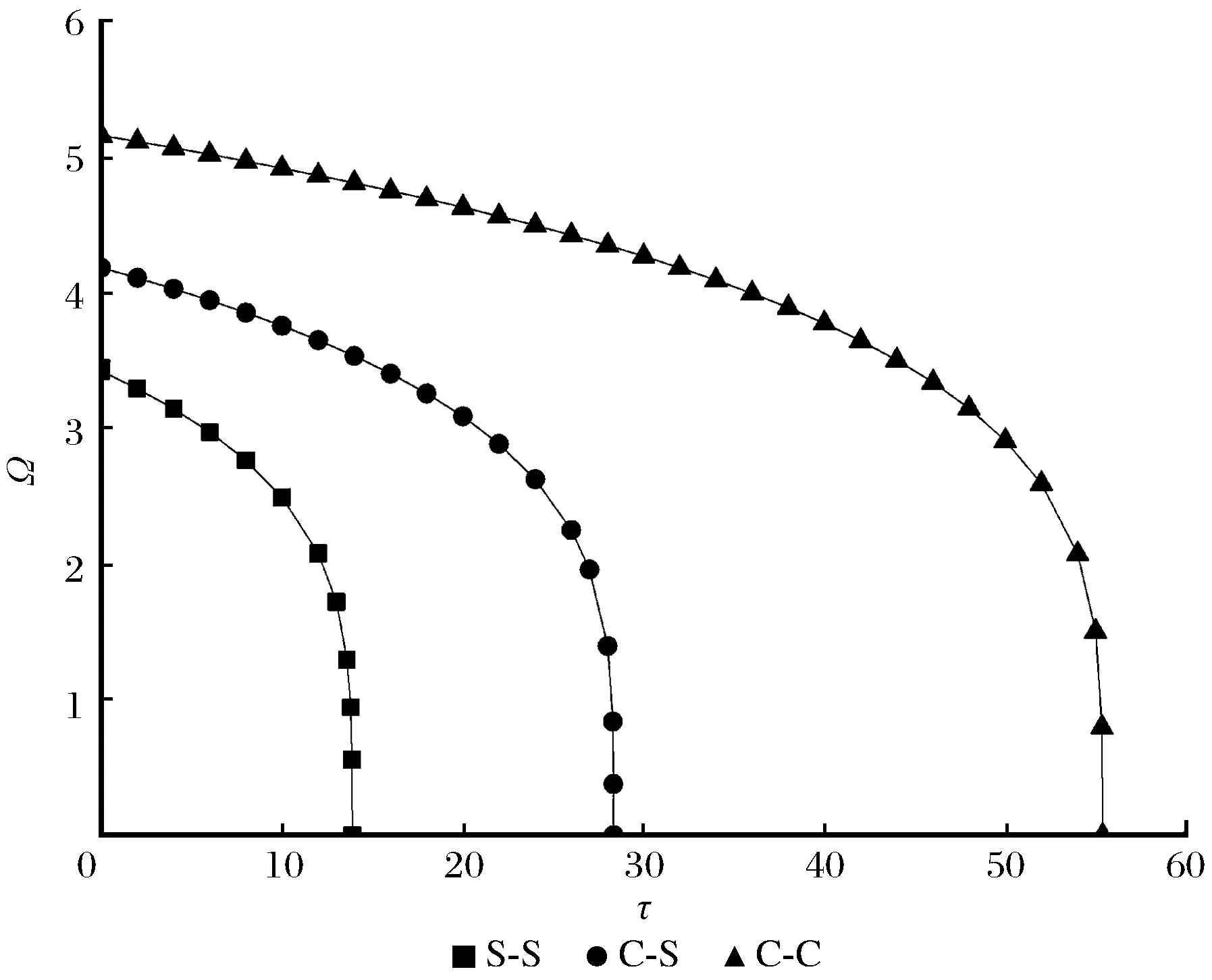
图2 无量纲升温τ对1阶无量纲固有频率的影响(β=0.4)

图3反映了当无量纲升温τ=4时截面变化系数β对1阶无量纲频率的影响,从图3中可以看出当截面系数β从0～0.5不断增大时,1阶无量纲频率随截面系数β的增大而缓慢增大。图4给出了不同截面变化系数时梁达到热屈曲状态的无量纲临界温度τcr。由图4可见3种边界条件下截面变化系数β越大,无量纲临界温度τcr越大,C-C边界条件下,截面系数增大的同时无量纲临界温度的变化最明显。