疲劳荷载作用下锈蚀钢筋混凝土墩柱的轴心受压承载力试验研究

陈 妤，李向楠，李星辰，蒋俊南

(江苏大学，土木工程与力学学院，镇江 212013)

0 引 言

随着经济的发展，海洋工程建设的进程不断推进。恶劣的海洋环境使得结构承受各种化学作用(氯盐侵蚀等)和物理作用(风浪等)，严重降低工程结构的耐久性和安全性。因此，对疲劳荷载作用下锈蚀钢筋混凝土柱的承载力研究具有一定的意义。

国内外对混凝土柱承载力的试验研究环境条件以静载和化学腐蚀为主，董行[1]用电化学加速锈蚀方法得到锈蚀钢筋混凝土构件缩尺模型，提出了无箍筋段锈胀钢筋混凝土结构极限承载力公式。邢国华等[2]在修正反复荷载作用下钢筋混凝土柱分析模型的基础上，提出了锈蚀钢筋混凝土柱压-剪-弯交互作用下的极限承载力计算模型。孙香花等[3]研究了轴压荷载和硫酸盐、氯盐侵蚀耦合作用下钢筋混凝土柱承载力的退化规律，并通过纤维网格划分建立了承载力计算公式。李文等[4]考虑碳化残量、钢筋起锈时间和钢筋锈蚀速率等因素，得到了与服役时间有关的钢筋混凝土柱承载力计算公式。陈少杰等[5]考虑截面损伤和主筋压屈的影响，提出了仅考虑箍筋锈蚀影响因素下的钢筋混凝土柱承载力计算模型。Ding[6]对电化学腐蚀下碳纤维加固混凝土柱、玻璃纤维加固混凝土柱和普通柱的承载力进行了对比。Campione等[7]提出了腐蚀钢筋混凝土柱的轴心受压承载力计算公式，测试了不同截面形式和钢筋布置方式的柱的承载力，并与理论值进行比较。Li等[8]通过柱的侧向疲劳和外加电流钢筋锈蚀试验，发现钢筋锈蚀降低了柱的强度、延性和低周疲劳寿命。

各国的混凝土结构设计规范均给出了轴心受压承载力计算公式，影响其大小的主要参数依次是混凝土抗压强度、混凝土截面面积、钢筋强度和钢筋截面面积，我国规范[9-10]还考虑了可靠度、承载力安全系数和试件稳定性，美国规范(ACI-318-14)[11]则补充了强度折减、等效矩形应力图的图形系数和荷载偶然偏心的影响，欧洲规范(BS EN 1992-1-1:2004)[12]考虑了钢筋屈服时混凝土承载力已减小的影响。在耐久性设计方面，各国规范都根据设计使用年限和环境类别进行耐久性设计，对混凝土材料、试件保护层厚度等提出相应的耐久性要求，针对处于恶劣环境下的试件采取耐久性技术措施。

由前述可知，目前关于钢筋混凝土柱的承载力研究大多基于材料本身，而且试验环境以静载和化学腐蚀为主，涉及到混凝土柱疲劳试验的研究偏向于抗震性能，对锈蚀普通混凝土柱在疲劳荷载作用下的承载力试验研究相对较少。此外，混凝土结构设计规范中提出的非预应力普通箍筋轴心受压承载力计算公式基本未考虑耐久性因素的影响，规范中提到的耐久性要求和技术措施主要是服务于设计阶段，对处于服役期的结构承载力进行评估可以方便后期的检测和维护，因此，恶劣环境下试件的承载力研究具有重大意义。本课题旨在研究锈蚀柱在疲劳荷载作用下的承载力，对11根锈蚀柱进行了轴心受压试验，分析了锈蚀率、疲劳加载频率对混凝土承载力的影响，最后给出在锈蚀柱在疲劳荷载作用下的承载力计算公式，且公式计算值与试验值相近。

1 实 验

1.1 试件设计

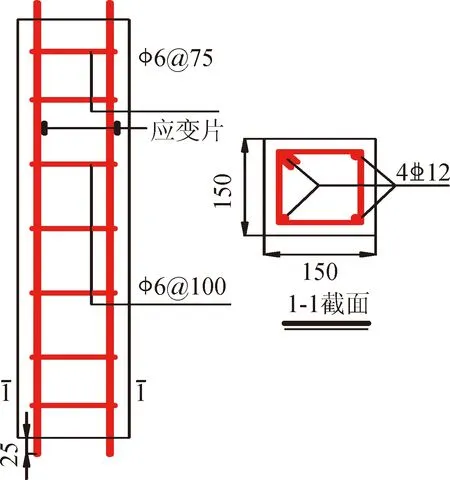
图1 试件配筋图(Unit：mm)Fig.1 Reinforcement diagram of member

试验设计了11根钢筋混凝土墩柱，柱高650 mm，柱截面尺寸为150 mm×150 mm，试件长细比为4.3，试件配筋图见图1。纵筋采用直径为12 mm的HRB400，两端伸出钢筋长25 mm，便于通电锈蚀，箍筋选用直径为6 mm的HPB300，为防止通电锈蚀过程中箍筋锈蚀，箍筋与纵筋接触点做了绝缘处理，实测钢筋力学性能参数如表1所示。

混凝土强度为C30，保护层厚20 mm，水胶比为0.46，粗骨料为粒径5～15 mm的碎石，细骨料采用细度模数为2.3的河砂，配合比见表2。实测立方体抗压强度平均值fcu为34.1 MPa，由规范[13]相关公式可得，混凝土轴心抗压强度fc为25.9 MPa。

表1 钢筋性能参数Table 1 Performance parameters of steel bar

表2 混凝土配合比Table 2 Mix proportion of concrete /(kg/m3)

1.2 加速腐蚀试验

采用恒电流加速锈蚀法，将试件水平浸泡在质量分数为5%的氯化钠溶液中，保证伸出钢筋高于液面2 cm，用同浓度氯化钠溶液湿润海绵盖在试件表面，阳极钢筋和阴极不锈钢片并联之后与电源相连，如图2所示。

图2 通电加速锈蚀现场Fig.2 Electrified accelerated corrosion site

图3 腐蚀电流密度测试Fig.3 Corrosion current density test

依据Faraday定律，控制通电时间使试件获得不同的理论锈蚀率。文献[14]提出，为了避免产生与自然锈蚀明显不同的锈蚀特征，电流密度应控制在200～300 μA/cm2。因此，本试验的电流密度设定为0.3 mA/cm2，每2 d使用钢筋锈蚀测定仪测量钢筋腐蚀电流密度，预估锈蚀程度，测试过程见图3。钢筋通电锈蚀情况表见表3。

表3 钢筋通电锈蚀情况Table 3 Electrified corrosion of steel bar

1.3 疲劳加载试验

通过未锈蚀试件的弯曲静载试验，测得其极限承载力平均值Pu为90 kN，荷载上限取0.85Pu，荷载下限取0.17Pu，疲劳应力比为0.2，加载频率选取1 Hz和3 Hz。根据《混凝土结构设计规范》[9]，混凝土最大疲劳应力为3.8 MPa，混凝土轴心抗压疲劳强度为20.72 MPa,满足钢筋混凝土受弯试件正截面疲劳应力验算的要求。通过疲劳破坏试验，确定试件0-1-a的疲劳寿命nf为44 104次，试件疲劳加载次数取0.5nf，保证试件产生一定的疲劳损伤但不发生破坏。正式加载之前进行预加载，保证试件、传力装置、支座和MTS试验机之间接触良好。将混凝土应变片连接到静态应变仪上，每隔3 600次在荷载处于下限时暂停5 min，期间记录残余应变，加载参数如表4所示，疲劳荷载水平为疲劳荷载上限与弯曲静载极限承载力的比值；疲劳应力比为疲劳荷载下限与疲劳荷载上限的比值。

表4 试件试验参数Table 4 Test parameters of specimen

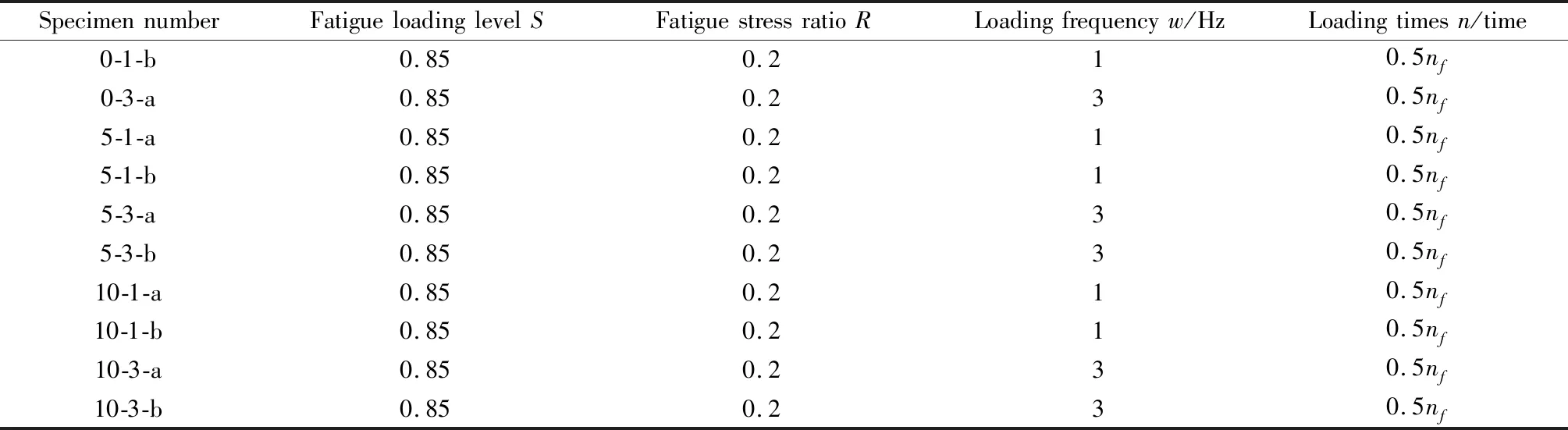
续表4

注：试件编号的第1个数字对应理论锈蚀率，第2个数字对应疲劳加载频率，a、b区分相同工况的两根试件；nf为试件0-1-a的疲劳寿命。

1.4 轴心受压承载力试验

图4 加载现场Fig.4 Loading site

试验前将两端伸出钢筋切割掉，试验在YEW-5000F液压压力试验机上进行，加载现场如图4所示。

加载前严格物理对中，并预加荷载20 kN，同时检查位移计读数是否正常，满足要求后，卸载完进行正式加载。根据《混凝土结构试验方法标准》[13]对验证性试验的规定，进行分级加载，在开裂荷载前每级加载值为50 kN，试件开裂后每级加载值取25 kN，直到试件压溃，结束加载。

1.5 测定实际钢筋锈蚀率

承载力试验结束后，将试件破形，取出钢筋，先采用稀盐酸清洗表面，并用钢丝刷配合除锈，铁锈清理完用少量石灰水除去残余盐酸，然后用酒精清洗，干燥完称量。实际钢筋锈蚀率为：

(1)

式中，m和m′分别为钢筋初始质量和锈后剩余质量。

计算得到的实际钢筋锈蚀率见表5。

表5 实际钢筋锈蚀率Table 5 Actual corrosion rate of steel bar

由表5可知，实际锈蚀率与理论锈蚀率平均相差36%和26%，通电时间越长，锈蚀程度越严重，两者就越接近。主要在于虽然箍筋与纵筋接触处作了绝缘处理，但在混凝土振捣过程中部分绝缘胶带会脱落，导致箍筋也耗散了电流；文献[15]指出极化电阻法本身仅适用于均匀腐蚀的测试，但氯盐侵蚀过程中钢筋发生不均匀锈蚀。

2 结果与讨论

2.1 疲劳加载下残余应变的变化规律

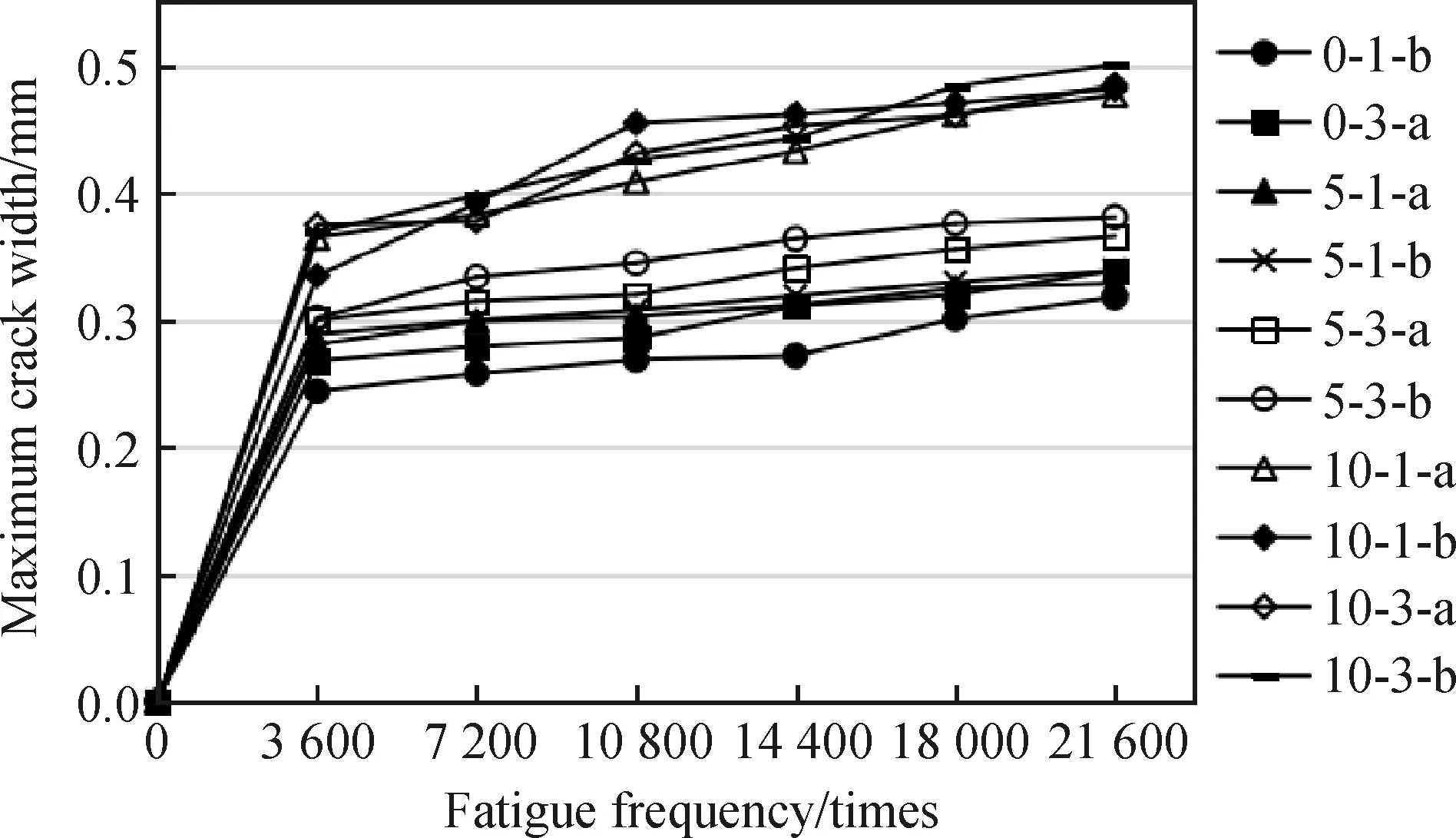
图5 疲劳次数对残余应变的影响Fig.5 Influence of fatigue degree residual

残余应变随疲劳次数变化的关系如图5所示，从图中可以看出，第一阶段，残余应变迅速发展；第二阶段，残余应变稳定增长，与文献[16]所述的混凝土疲劳残余应变三阶段特性相符。

由图5可知，疲劳荷载作用下，随着锈蚀率的增大，经历21 600次疲劳后混凝土的残余应变显著增加，但对加载频率的敏感性降低。与未锈蚀的试件相比，理论锈蚀率为5%和10%的试件的混凝土残余应变值平均增幅分别为13.7%和30%。加载频率为3 Hz，理论锈蚀率为5%、10%的试件，混凝土残余应变依次增加14.3%～16.4%、28.8%～29.1%；与未锈蚀的试件相比，加载频率为1 Hz，理论锈蚀率为5%、10%的试件，混凝土残余应变依次增加10.8%～13.4%、28.30%～33.5%；疲劳荷载作用下，随着加载频率的增大，经历21 600次疲劳后混凝土的残余应变均有小幅的增加。理论锈蚀率为5%时，随着加载频率的增加，混凝土残余应变的增幅略微升高；理论锈蚀率为10%时，混凝土残余应变的增幅与加载频率无关。这是由于锈蚀率越高，钢筋的缺陷也越多，导致本身的耗能能力下降，且钢筋与混凝土的粘结力大幅下降，锈蚀产物使试件产生更多的微裂缝，造成多处应力集中，促使裂纹的扩展。

2.2 短柱受压破坏形态

在加载初期，试件表面裂缝闭合，横向位移较小；继续加载，柱端出现裂缝且向中部扩展，保护层剥落，横向位移逐步增大；当加载值接近极限荷载时，裂缝迅速发展，混凝土被压碎。试件破坏过程基本相同，裂缝出现在钢筋附近。

结合图6可以发现，未锈蚀试件裂缝较短且多为不连续，混凝土局部压碎，破坏表现为脆性；锈蚀试件的裂缝扩展更迅速，混凝土剥落更严重，破坏表现为更明显的脆性。主要在于锈蚀钢筋的力学性能下降，且钢筋与混凝土的粘结力大幅下降，导致持续的受压荷载下，混凝土与钢筋之间过早发生应力重分布，纵筋更快发生屈曲，混凝土被压碎。

图6 试件破坏形态Fig.6 Failure form of specimens

3 通电锈蚀和循环加载作用下RC柱的轴心受压承载力计算

3.1 基本假定

参考《混凝土结构设计规范》[9]，在进行承载力计算时，采用以下基本假定：

(1)短柱在受压过程中截面保持平面。

(2)不考虑混凝土的抗拉强度。

(3)受损钢筋的应力应变关系仍符合虎克定律。

(4)不考虑通电加速锈蚀过程中箍筋的锈蚀。

(5)忽略混凝土损伤对承载力的影响。

3.2 极限承载力计算公式

根据规范[9]，主要考虑钢筋屈服强度和截面面积对承载力的影响。

3.2.1 锈蚀钢筋屈服强度

根据张伟平等[17]作的锈蚀钢筋应力-应变关系研究，发现试件通电流锈蚀过程中，当锈蚀率达到30%时，变形钢筋的屈服平台退化，本试验的锈蚀率小于40%,故锈蚀钢筋的屈服强度为:

(2)

式中,f′y、fy分别为锈蚀钢筋屈服强度和未锈蚀钢筋屈服强度，η0为实际锈蚀率。

3.2.2 锈蚀钢筋截面面积

参照王雪慧等[18]得到的钢筋的质量损失率和截面损失率的关系表达式，本试验中的实际锈蚀率满足2%<η0<10%的区间，截面锈蚀率与质量锈蚀率的关系：

ηs=0.015+0.97η0

(3)

截面锈蚀率：

(4)

式中,A′sc、A′s分别为锈蚀钢筋的截面积和未锈蚀钢筋的截面积，ηs、η0分别为截面锈蚀率和质量损失率。

由式(3)和(4)可得：

A′sc=(0.985-0.97η0)A′s

(5)

3.2.3 疲劳荷载后的锈蚀钢筋截面面积

文献[19]推导了钢筋疲劳的本构模型。当钢筋的疲劳强度退化到疲劳破坏允许的最大应力时，钢筋断裂，破坏准则如下：

σ≤σmax

(6)

结合等效应变准则，可得钢筋疲劳断裂时的有效截面积为：

(7)

根据P-M线性累积损伤理论，等幅疲劳荷载下，循环加载n次后钢筋面积疲劳损伤为：

(8)

钢筋在经历n次循环后的有效截面面积为：

(9)

式中，σ为疲劳加载后的钢筋疲劳剩余强度；σmax为钢筋疲劳破坏所允许的最大应力值；Asf为钢筋疲劳破坏时剩余有效面积；D为损伤度；n为疲劳加载次数；N为疲劳寿命；A′scf为钢筋在经历n次循环后的有效截面面积。

3.2.4 疲劳荷载后的锈蚀钢筋屈服强度

结合破坏准则，得钢筋在任意循环次数下的屈服强度为：

(10)

结合钢筋S-N曲线进行修正，钢筋经历n次循环后的屈服强度为：

(11)

3.3 RC柱轴心受压承载力

(12)

式中,φ为稳定系数，fc、f′yf分别为混凝土轴心抗压强度和锈蚀钢筋疲劳后的屈服强度，A、A′scf分别为柱截面面积和疲劳后锈蚀钢筋的截面面积，纵向受力筋需分开计算。

3.4 轴心受压承载力理论值与试验值的对比

参考《混凝土结构设计规范》[9]，钢筋应力幅计算公式如式(13)与式(14)所示：

(13)

(14)

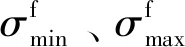
RC柱疲劳试验时相当于单筋矩形截面梁(受压区相当于布置架立筋)，按式(15)计算：

α1fcbx0=fyAs

(15)

式中,α1为受压区等效矩形应力图形系数；fc为混凝土抗压强度；b为柱宽；fy为钢筋抗拉强度；As为主筋截面面积。

由式(15)得，x0=24 mm，计算长度为530 mm，传力装置长180 mm，则钢筋的疲劳应力上下限分别为229 MPa和46 MPa。

夏晓慧等[20]收集了国内外钢筋混凝土梁的锈蚀数据，建立了不同锈蚀速率下钢筋混凝土梁的S-N曲线。

未锈蚀，发生低周疲劳时，S-N曲线如式(16)所示：

lgN=15.56-3.99lgΔσ

(16)

式中,N为钢筋疲劳失效次数；Δσ为应力幅。

由式(16)得,N=3 410 516。

理论锈蚀率为5%，发生低周疲劳时，S-N曲线如式(17)所示：

lgN=14.82-3.89lgΔσ

(17)

由式(17)得，N=1 044 877。

理论锈蚀率为10%，发生低周疲劳时，S-N曲线如式(18)所示：

lgN=12.88-2.98lgΔσ

(18)

由式(18)得，N=1 373 712。

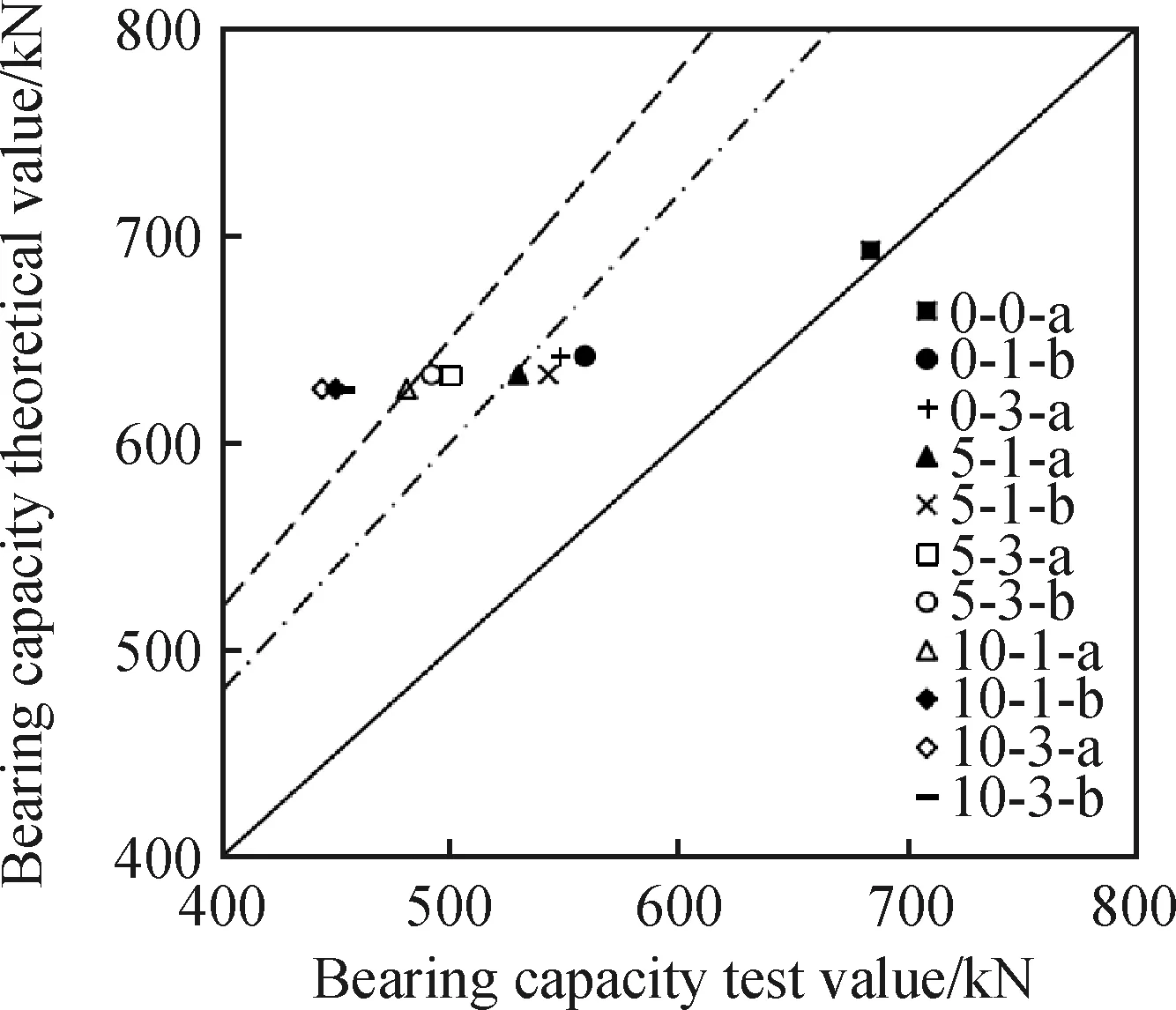
图7 本试验承载力理论值与试验值对比Fig.7 Comparison of bearing capacity between theoretical and experimental values in this experiment

综上，RC柱轴心受压承载力的理论值与试验值的对比如图7所示。

从左上到右下的直线分别代表误差为30%、20%、10%，由图7可知，当试件未锈蚀时，误差为1%。当理论锈蚀率为5%时，误差在0%～30%之内。当理论锈蚀率为10%时，误差在30%～40%之内，11根试件的理论值均大于试验值。主要是由于计算公式未考虑混凝土的影响，当锈蚀率较小时，混凝土损伤对承载力的影响较小，误差相对较小；当锈蚀率较大时，钢筋与混凝土界面粘结力急剧下降，混凝土性能退化严重，混凝土因素不容忽视，误差相对较大。

为了进一步验证在基本假定条件下疲劳荷载作用下锈蚀钢筋混凝土柱轴心受压承载力计算公式的合理性，收集了部分学者的试验结果与式(12)得出的理论值进行对比，如图8所示。

从图8中可以看出，理论值与试验值基本吻合，文献[21]的误差大多小于6%，文献[22]的误差均小于25%，理论值与试验值比值的均值为0.97，变异系数为0.2，因此式(12)在锈蚀率0%～10%的区间内是合理的。但式(12)仅考虑了钢筋性能退化对承载力的影响，而混凝土性能的退化以及钢筋与混凝土粘结力的降低也不容忽视，并且实际工程与室内试验存在差异，因此，公式需要进一步完善。

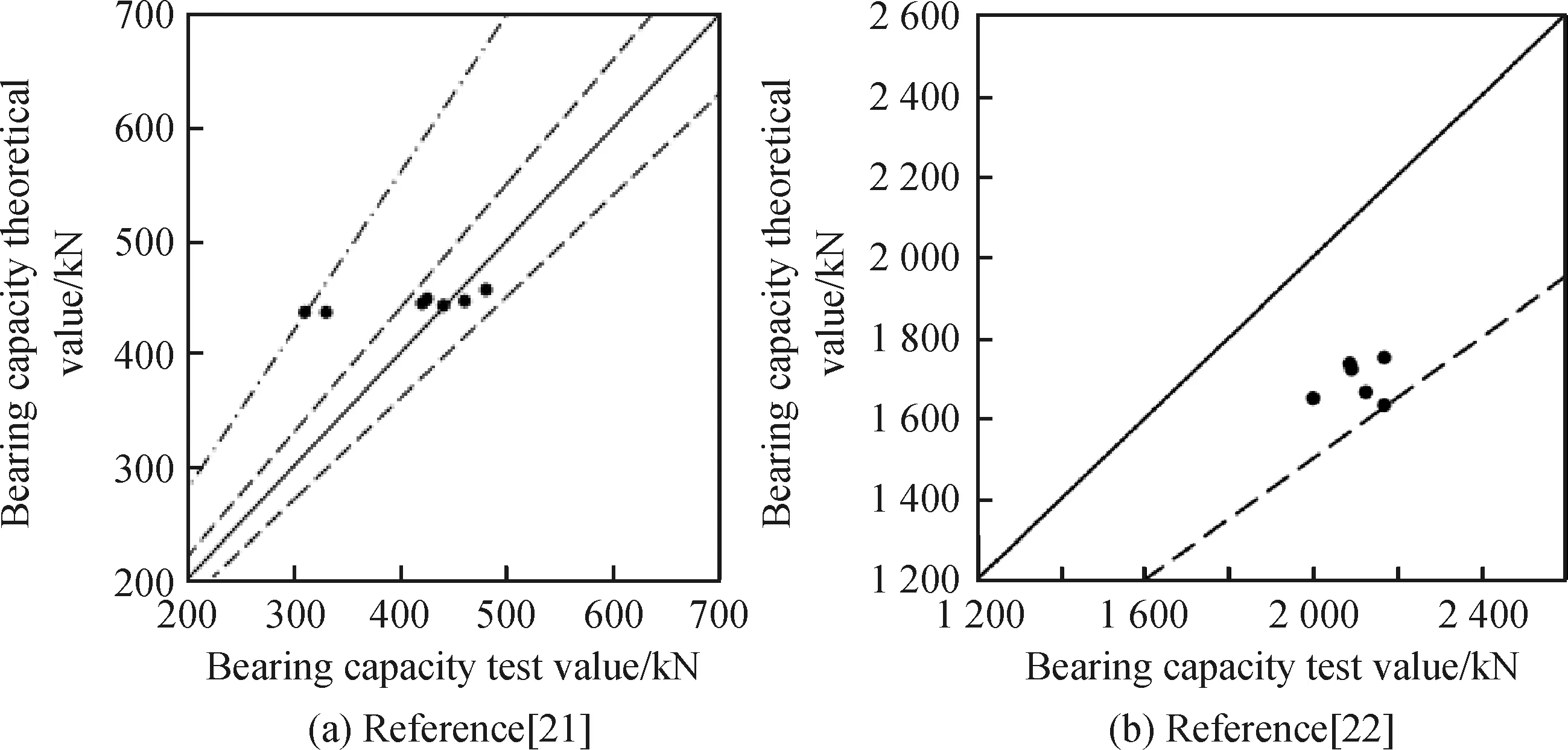
图8 部分学者承载力理论值与试验值对比[21-22]Fig.8 Comparison of bearing capacity between theoretical and experimental values in some scholars’ experiments[21-22]

4 结 论

(1)疲劳加载过程中，锈蚀率恒定，随着加载频率的增大，经历一定疲劳次数后的混凝土残余应变小幅增加；加载频率恒定，随着锈蚀率的增加，经历一定疲劳次数后的混凝土残余应变显著增大，但对加载频率的敏感性降低，锈蚀率对混凝土残余应变的影响相对较大，锈蚀率越高增幅越明显，与未锈蚀试件相比，理论锈蚀率为5%和10%的试件平均增幅分别为13.7%和30%。

(2)试件受压时，未锈蚀试件出现不连续的且较短的裂缝，破坏表现为脆性，锈蚀试件的裂缝扩展很迅速，混凝土剥落更严重，破坏时为更明显的脆性。

(3)通过试验值与理论计算值的对比，在基本假定条件下，推出的疲劳荷载作用下锈蚀钢筋混凝土柱轴心受压承载力计算公式基本合理。