机场出租车司机决策问题研究
2020-06-18魏逸凡东北电力大学理学院
魏逸凡 东北电力大学理学院
1 .引言
近年来,随着我国经济水平的不断提高,全社会运输需求增加,航空运输作为现代交通体系中较为快捷的运输方式,受到了广泛欢迎。机场作为航空运输的基础,具有垄断性、稀缺性的特点,在我国得到了极大发展。随着我国机场数量的增多和航空运输需求的扩大,我国机场业务量保持着快速稳步增长态势,旅客吞吐量增速超过10%,货邮吞吐量保持稳步提高。
2 .模型建立与求解
2.1 模型的建立
2.2.1 出租车司机决策因素机理分析
在乘客下机后要去周边的目的地,出租车是主要的交通工具之一。送客到机场的出租车司机会在已知某时间段抵达的航班数量和“蓄车池”已有的车辆数的情况下做出决策。以下为两种决策方案:
(A)前往“蓄车池”等待载客返回市区,依据先来后到排队入场载客。
(B)直接返回市区拉客。
一般情况下,收益会成影响出租车司机决策的主要因素,司机会权衡方案A 与方案B 的收益与损失。选择方案A可以收获载客收益z,但是司机由于前往“蓄车池”等待,所以会付出隐形损失:时间成本k;而方案B 可以收获回市区后的接客收益,此收益为潜在载客收益s,但是由于回市区未拉到客人,所以会付出一定的空载费用l。
以下为出租车司机决策相关因素影响机理思维导图:
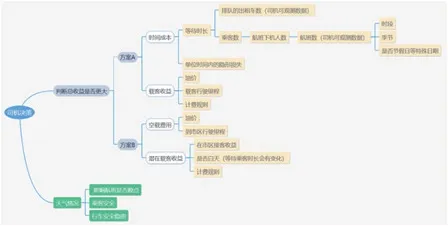
图1 出租车司机决策相关因素影响机理思维导图
2.2.2 方案A 的总体收益模型
(1)方案A 的基础模型
如果司机选择方案A,那么司机的总体收益QA为:QA=z-k(1)
其中,z 为载客收益,k 为时间成本。
(2)方案A 的总体收益
载客收益z 与当地的油价、载客行驶里程u 与当地的出租车计费规则有关,当地的油价与当地的出租车计费规则为定值。假设载客行驶里程u 服从范围为[r1-r2,r1+r2]的泊松分布,其中r1为市中心到机场的距离,r2为城市半径。
由以上模型知,方案A 的总体收益为:

2.2.3 方案B 的总体收益模型
(1)方案B 的基础收益模型
如果司机选择方案B,那么司机的总体收益QB为:
QB=s-l (3)
其中,s 为潜在载客收益,l 为空载费用。
(2)空载费用与潜在收益模型
空载费用l 由油价与司机空载到市区的行驶里程决定。油价为当地出租车的平均油价。这里假设司机空载到市区的行驶里程与到市区载客行驶里程u 独立同分布,均服从范围在[r1-r2,r1+r2]的泊松分布。其中r1为市中心到机场的距离,r2为城市半径。
潜在载客收益s 为在出租车司机在空载返回之后进行载客,从而形成潜在的载客收益。潜在载客收益s 与在市区的载客收益z'与在市区等待载客时长tj有关。在市区的载客收益z'与当地的油价、市区载客行驶里程u'与当地的出租车计费规则有关。当地的油价与出租车计费规则均为定值。假设市区载客行驶里程u'服从范围为[3, 2*r2]的泊松分布,即假设乘客均在城市范围内活动且最小行驶里程为3 km。
2.3 模型的求解
2.3.1 出租车司机选择决策模型
出租车司机选择A 方案与B 方案的主要因素是收益,天气也是出租车司机进行选择的因素之一。但是由于天气因素多变,且如下雨、下雪等天气由于程度不同,影响判断的参数难以一一量化,所以本文假设模型的前提为不会遇到对司机决策影响过大的天气,如果遇到司机会直接选择B 方案或直接回家。
出租车司机选择A、B 方案收益之差Z 为:
Z= QA-QB(4)
将方案A的总体收益模型与方案B的总体收益模型带入式(4),即有:

其中,z 为载客收益,l 为空载费用,s 为潜在载客收益,b 为“蓄车池”车量数,f 为单位时间内的隐形损失,M 为当前时段的客机平均最大容量,N 为当前时段客机的数量,θ为客座利用率,β为可决系数。
决策Dec 为:
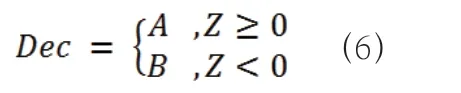
A 即为选择A 方案,B 即为选择B 方案。当Z=0 时,考虑到在停车场等待司机会付出较少的精力,所以将其划入A 方案中。
2.3.2 司机选择策略方案
由出租车司机的选择决策模型中可以看出,载客收益z 与空载费用l 由油价与司机的行驶里程决定。出租车司机在选择A 方案时,会出现载客收益z,我们假设了司机载客行驶里程u 服从范围在[r1-r2,r1+r2]的泊松分布,所以为有区间的随机值。司机在选择B 方案时,会出现空载费用l,司机空载到市区的行驶里程与到市区载客行驶里程u 独立同分布,均服从范围在[r1-r2,r1+r2]的泊松分布,所以也为有区间的随机值。
总体收益模型的最后一项参数有:“蓄车池”车量数b、单位时间内的隐形损失f、当前时段的客机平均最大容量M、当前时段客机的数量N、客座利用率θ、可决系数β。最终司机的选择策略为:首先根据自己的经验判断出可决系数的大小,然后观察“蓄车池”车量数与当前时段客机的数量,最后将相应数值代入出租车司机选择决策模型即可判断出A 方案还是B 方案为最优方案。
