测控系统相位噪声对测速的影响分析

勾习睿

(沃金森学校，美国 哈特福德 53027)

测控系统中，频率源短稳会引起系统的测速误差。频率源短稳的时域描述是用阿伦方差表示，频域描述在实际测量时用相位噪声表示，而在理论分析中常用相位起伏谱密度表示。因此，在工程核算系统频率源短稳引入的系统误差时，需要进行相位噪声、相位起伏谱密度和阿伦方差之间的换算。本文讨论了阿伦方差、相位起伏谱密度和相位噪声的关系，并给出了工程核算时使用的简化算法。

1 阿伦方差

David Allan 于1966年提出了Allan方差，最初该方法用于分析振荡器的相位和频率不稳定度。假设频率源输出的信号为：

V(t)=[V0+A(t)]sin[ω0t+φ(t)]

(1)

(2)

式中，〈〉表示T=τ的无限时间平均，σ2(2,τ,τ)表示无间隙阿伦方差。

若相邻两次测量存在时间间隙，则两次测得的相对频率的方差称为有间隙阿伦方差σ2(2,T,τ)(T≠τ)，有间隙阿伦方差和无间隙阿伦方差用巴纳斯(Barnes)偏移函数相联系。

2 相位起伏谱密度

式(1)中，A(t)和φ(t)分别代表随机因素所产生的幅度调制和相位调制。幅度调制不影响频率稳定度，其所产生的噪声远小于相位调制产生的噪声，因此常用边带的相位起伏谱密度表述频率稳定度。当调制由噪声产生时，Δφrms决定于噪声电压有效值，其值可能随偏离载频的频率不同而异,即是fm的函数，因此，相位起伏谱密度定义为[2]：

(3)

在式(3)中，Δφrms(fm)表示偏离载波频率fm处的相位起伏大小的有效值，通常记为Rad，Bn表示计算等效噪声的分析带宽，其单位为Hz，因此相位起伏谱密度的单位为rsd2/Hz。

3 相位噪声

相位噪声是指系统在各种外部环境噪声的作用下，所引起的频率源输出信号相位的随机变化。目前工程中，由美国国家标准协会(ANSI)所定义的单边带相位噪声L(fm)为相位噪声较为广泛的表征形式[3]，其定义如下所示：

(4)

或者以分贝形式表示如下：

(5)

其中PSSB(fm)表示偏离载波Δf处1 Hz带宽内信号的噪声调制边带功率，P0表示载波信号的总功率，图1为单边带相位噪声功率谱L(fm)的示意图。

4 阿伦方差、相位起伏谱密度、相位噪声的关系

4.1 相位起伏谱密度和相位噪声的关系

对于正弦频率调制信号而言，其瞬时频率与瞬时相位分别表示为:

f(t)=f0+Δfvcos(2πft)

(6)

(7)

式中Δfv表示最大频偏，f则为调制频率，令Δφ=Δfv/f表示最大相位偏移或者叫做调制指数，因此可得到相位调制信号为：

V(t)=V0cos(2πf0t+Δφsin(2πft))

(8)

用贝塞尔函数将(8)式展开为级数表达式为：

(9)

通常情况下有Δφ1rad，因此式(9)可以被简化为：

(10)

由式(10)可知，相位调制信号与载波信号的相位正交。并且两个边带信号间是互为反向的，边带信号的幅度与载波信号的幅度之比可以表示为：

(11)

通过公式(11)可知，边带信号与载波信号的功率之比可以表示为：

(12)

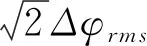
(13)

对数表达式为：

(14)

式(14)中单位为dBc/Hz。

4.2 相位起伏谱密度和阿伦方差的关系

很多文献都给出了相位起伏谱密度和阿伦方差的关系[4-6]:

(15)

式中τ为测量阿仑方差的采样间隔时间，单位为s；f为偏离载频f0的频率间隔，单位为Hz；Sφ(f)为相位起伏谱密度。

美国电子与电气工程师学会IEEE推荐使用相位起伏谱密度Sφ(f)的幂率谱模型来描述振荡器的相位噪声特性，其包括叠加在一起的五种独立噪声过程，其模型为：

(16)

由于上式中的各项都正比于f的各次幂，故称为幂率谱。

与频域类似，在时域中，阿仑方差幂率表达式为：

(17)

其中μ为各次幂，μ=-α-1(当α≥1时，μ=-2)，它在时域上表征了频率起伏噪声的类型，而Kα与hα相对应，它表征了各类噪声的强度。

这五种噪声类型与谱密度的关系如表1所示。

表1 五种噪声的谱密度

噪声类型αSφ(f)μ阿伦方差调相白噪声2h2f20-2K+2τ-2调相闪烁噪声1h1f20f-1-2K+1τ-2调频白噪声0h0f20f-2-1K0τ-1调频闪烁噪声-1h-1f20f-30K-1τ0频率随机游动-2h-2f20f-41K-2τ+1

5 工程估算

从上面的分析可以看出，通过相位起伏谱密度可以实现相位噪声和阿伦方差之间的转换。

工程上常将(16)式近似表示为下列对数表达

式：

(f1～f2为频率随机游动噪声)

(18)

(f2～f3为调频闪变噪声)

(19)

(f3～f4为调频白噪声)

(20)

(f4～f5为调频闪烁噪声)

(21)

(f5～f6为调相白噪声)

(22)

幂律谱折线近似的曲线图如图2所示。图中横坐标为f对数坐标，纵坐标为Sφ(f)对数坐标。

式(18)～(22)是工程中相噪指标的近似表示方法，令lgf=0，即可求出式(18)～(22)中的h-2、h-1、h0、h+1、h+2等，即

上式中的k-2、k-1、k0、k+1、k+2分别为h-2、h-1、h0、h+1、h+2各类噪声的近似折线与lgf=0时的纵坐标轴的交点值。

(23)

式中f6为计算短稳时积分运算的截止频率，它对应于相噪可产生作用的有效带宽，例如在锁相接收机中，它为锁相环的单边带宽。

(24)

同理可积分求出下列各项

调相闪烁噪声：

(当2πτ(f5-f4)>>1时)

(25)

调频白噪声：

(26)

调频闪变噪声：

(27)

频率随机游动：

(28)

求出5项阿仑方差后，总的阿仑方差为：

(29)

计算出阿伦方差后，便可以根据公式(30)[8]求出相位噪声对测速的影响。

(30)

式中B2为巴纳斯第二偏移函数，B2与μ和γ的关系如表2所示。其中μ为幂次，γ=T/τ(T为测控系统双向距离测量的时间，τ为积分时间)

表2B2与μ和γ的关系表

下面举例说明实际工程中相噪对测速误差的影响。

实际S频段测控系统中，系统频率源相噪指标如表3所示。

表3 系统频率源相位噪声

频偏相位噪声10 Hz-55d Bc/Hz100 Hz-70 dBc/Hz1 kHz-80 dBc/Hz10 kHz-90 dBc/Hz100 kHz-100 dBc/Hz

系统由式(29)～(32)和(35)～(38)得(系统频率按2 200 MHz，τ为50 ms计算)：

σy(τ)+2=2.449×10-11

σy(τ)+1=2.2825×10-11

σy(τ)0=4.5455×10-11

σy(τ)-1=3.0096×10-11

测速误差σR=0.995cm/s

6 结语

由于工程中，频率源短稳在时域很难测量，而使用频谱分析仪可以简便地测量频率源的相位噪声，因此，本文讨论了频率源短稳时域和频域的转换关系，给出了工程计算的简便估算方法，可以很方便地计算出频率源短稳对系统测速误差的影响。