环境规制、技术创新与就业增长的内在联系——基于中国34个细分工业行业PVAR模型的实证检验

朱金生，李 蝶

(武汉理工大学 经济学院，湖北 武汉 430070)

一、引言

改革开放40多年来，中国成为世界上第二大经济体和制造业大国，取得的辉煌成就举世瞩目。但是，中国经济在保持高速增长的同时，也付出了资源枯竭、环境污染和气候变化等代价。2018年，中国的全球环境绩效指数(EPI)得分为50.74，在180个国家和地区中排名第120位，这反映出经济快速增长给环境带来巨大的压力。面临日益严峻的环境问题，在达到环境承载力之前及时提高环境规制强度，是实现经济社会可持续发展的必然选择。然而，环境规制的实施必然会对经济社会产生一系列影响。除了生态效应和经济效应外，环境规制会产生潜在的就业负效应。技术创新是实现环境保护和经济发展双赢目标的决定因素，是经济长期绿色发展的关键驱动力。但是，人工智能等新技术的发展对就业的可能冲击成为重要的政策话题。中国正处于经济新常态的“三期叠加”大环境，经济下行、结构调整和消化过剩产能等可能引起的失业问题十分严峻。要实现生态、经济和民生相协调的可持续发展，必须既使得环境得到改善，又要兼顾到经济发展和民生保障。技术创新是经济发展的源泉，劳动就业是民生的基础，因此，对环境规制、技术创新和劳动就业三者的关系和相互影响进行研究十分必要。

环境规制与技术创新关系的争论由来已久，大部分的文献验证了环境规制的创新补偿效应。研究表明，环境规制对工业行业技术创新的影响呈现先抑制后促进的“U”型特征，并且存在行业异质性[1]。学术界一致认为环境规制对就业的影响存在两种机制，即负向的规模效应和正向的替代效应。早期的研究主要侧重于规模效应，并且得出结论认为，环境规制会提高企业的生产和治理成本，削弱企业的竞争优势，进而导致企业规模缩小，降低劳动需求。但是，环境规制在提高资源类生产要素价格时，企业会倾向于劳动密集型的生产性投入，从而增加了劳动力要素，进而产生替代效应[2]。因此，环境规制的就业效应取决于规模效应和替代效应的大小。随着研究的深入，学者们研究发现环境规制对就业的影响在不同国家、地区、行业都呈现出不同的特征。从行业层面看，环境规制对就业的影响在行业间存在异质性，会引起行业间的劳动力流动，使得各个行业之间存在联动作用[3]。新一轮产业革命带来生产方式和产业组织等诸多变革，催生出众多新产业和新业态，我们称之为“创新经济”。一方面，创新经济能够创造大量新的就业岗位；另一方面，创新经济对就业产生挤压效应，带来就业冲击。近年来，人工智能、机器人等新技术迅猛发展，既为经济增长提供了新的动力，也引发了对“机器替代人”的恐慌，目前人工智能、机器人等技术进步对就业的破坏效应有限，但长期就业效应不容乐观[4]。一部分学者关注到目前工作对技术发展的敏感[5]，另外一部分学者探讨了创新活动可能产生的就业创造效应[6-7]。

虽然现有的研究在环境规制、技术创新和劳动就业的关系上进行了一些研究，但它们主要侧重于建立线性回归模型，以分析变量之间的单向影响关系，忽视了内生性和滞后性问题。因此，本文基于工业细分行业异质性的视角，将环境规制、技术创新、就业效应纳入同一框架，建立动态面板向量自回归模型(PVAR)，分析三者之间的长短期动态交互效应，以及考察三者动态关系在清洁行业与污染密集行业、高技术行业与中低技术行业间的差异。

二、文献综述

1．基于弱波特假说的探究

弱波特假说认为，设计良好的环境规制可以激励企业创新，在追求利润最大化的前提下，环境规制为企业施加了额外的约束条件，这些限制可能促使企业开展创新活动，在新的约束下降低生产成本。杰夫(Jaffe)和帕尔默(Palmer)采用美国工业行业数据，检验了以污染支出费用衡量的环境规制对R&D支出和专利申请量的影响，研究发现环境规制对研发支出具有显著的促进作用，但对专利申请的影响不显著[8]。部分学者通过仅对环境有关的专利申请量进行实证研究，发现了环境规制与专利申请的正向关系[9-10]。沈能等利用非线性阈值模型，分析了中国环境规制和技术创新的门槛效应，研究表明只有环境规制强度跨越特定门槛值时，波特假说才能实现[11]。蒋伏心等利用江苏省制造业行业的数据，采用GMM方法检验了环境规制强度对技术创新的影响，研究表明环境规制与企业R&D呈现先下降后提升的“U”型关系[12]。米拉尼(Milani)通过 28 个 OECD 国家的研发数据发现，难以转移的产业在面对环境规制增强时，将会选择开展更多的研发活动[13]。大部分的研究都支持了弱波特假说，即环境规制在一定程度上对企业的技术创新具有促进作用。

2.就业双重红利假说的验证

2009年《世界劳工报告》提出，环境规制能够实现改善环境的同时提高就业的双重红利。国内外关于环境规制与就业关系的研究主要存在以下三种观点：一是环境规制减少了就业数量。迪索(Dissou)等利用一般均衡框架分析了碳减排政策对劳动力需求的影响，结果表明当许可收入被转嫁给家庭时，碳减排政策对就业有负面影响[14]。二是环境规制增加了就业数量。米什拉(MiShra)和史密斯(Smyth)研究发现，环境规制作用于高劳动力需求产业如环保产业及相关服务业时，会增加劳动力需求，提高就业水平[15]。格雷(Gray)运用DID方法对美国制浆和造纸业条例产生的就业效应进行了评估，研究发现该项政策没有显著地减少就业，反而可能轻微地促进就业增加[16]。赵连阁运用联立方程模型估计了工业污染治理投资强度对地区就业的影响，实证发现污染治理投资有效地带动了就业增长[17]。三是环境对就业数量的影响不确定，或者存在先抑制后促进的关系。卡恩(Kahn)和曼苏尔(Mansur)认为，环境规制标准的差异造成就业的空间转移，会对不同区域就业造成不确定影响[18]。闫文娟等采用面板门限模型验证了环境规制对劳动就业影响的差异，研究表明，低水平的环境规制才能不损害就业，想要实现环境规制和就业双赢，提高第三产业比重是关键[19]。王勇等在莫根施特恩(Morgenstern)理论框架的基础上，引入了行业特征参数，验证了环境规制对不同行业就业的影响，发现二者之间存在“U”型关系，当环境规制跨过门槛值时会对就业产生促进作用[20]。李珊珊检验了环境规制对就业的影响和差异性，结果发现环境规制与就业之间存在“U”型动态关系[21]。李梦洁分析了多重影响机制下环境规制对就业的影响，研究发现环境规制和就业数量呈“U”型关系，行业异质性导致“U”型曲线的形状及位置存在明显差异[22]。随着研究的深入，学者们发现环境规制对就业的影响在不同国家、地区、行业都呈现出不同的特征。

3．创新对就业的影响：创造还是破坏？

技术创新对就业产生创造效应和破坏效应，哪一种效应占主导地位是决定技术创新对就业影响结果的重要因素。国内外有大量学者对技术创新与就业增长的关系进行了实证分析，选择的分析变量不同，技术创新对就业影响的研究结果也不同。从行业层面分析创新对就业数量的直接和间接影响，结果依赖于产品创新正向影响和工艺创新负向影响的综合作用。安东努斯(Antonucci)和皮安塔(Pianta )分析了8个欧洲国家制造业行业的就业增长方程，结果显示技术变革对制造业的就业产生了负面影响，但是对企业的竞争策略起到了积极作用，其中，技术竞争力来源于产品创新，价格竞争力来源于过程创新[23]。博利亚奇诺(Bogliacino)和皮安塔从行业水平验证了8个欧洲国家制造业和服务业技术创新和就业之间的关系，提出了一个修正的Pavitt分类方法用来分析技术变革具体模式的就业创造与破坏，发现了技术变化影响就业的不同机制[24]。国内关于行业或者产业层面分析技术创新就业效应的研究比较少见。方建国和尹丽波通过技术分解法和产业分解法分析了福建省制造业技术创新对就业的影响，研究表明技术变化对不同产业的就业影响不同[25]。张车伟等利用行业权重计算了创新经济的就业规模和拉动其他行业就业的规模，同时分析了创新经济对就业产生的挤压效应。

通过梳理已有文献可以发现，环境规制与技术创新具有密切联系，环境规制对劳动就业存在作用，技术创新是影响劳动就业的重要因素。在面临生态、经济和民生可持续发展的背景下，国内外鲜见将环境规制、技术创新和劳动就业三者纳入同一框架进行研究的。本文的创新之处在于：首先，将环境规制、技术创新和劳动就业纳入内生系统，建立动态面板向量自回归模型，分析三者的长短期效应，明确现阶段环境规制、技术创新和劳动就业关系的现状。其次，从行业异质性的视角出发，依据污染程度和技术水平对行业进行划分，检验环境规制和技术创新对不同类型行业就业水平的影响，以期针对不同细分行业制定差异化的环境规制政策和创新战略。

三、作用机理分析

1. 影响机制分析

从现有研究可以看出，环境规制、技术创新和劳动就业通过各种机制并且产生不同方向的作用交织在一起。为了研究环境规制、技术创新与劳动就业的动态关系，有必要先梳理环境规制对技术创新的影响机制、环境规制对劳动就业的影响机制以及技术创新对劳动就业的影响机制(见图1)。

(1)环境规制对技术创新的影响机制。环境规制对技术创新产生的影响存在两种机制，即正向的补偿效应和负向的抵消效应。一方面，企业需要大量的资金投入进行技术革新，环境规制标准增加了企业的污染治理成本，由于企业生产领域的资金投入是有限的，这将会对研发投入的资金产生挤出效应。同时，实施严格的环境规制可能会促使企业选择环境规制比较宽松的行业进行生产投资，从而对技术创新产生负向的抵消效应。另一方面，企业在执行环境规制措施或者改良污染治理技术降低污染排放量时，其污染治理成本会明显提高。在利润最大化的框架下，企业可能开展创新活动，在新的约束下降低成本。企业可以通过技术革新改良生产工艺或提高治污能力，提高企业的生产率水平，减缓或抵消政府环境规制给企业增加的环境成本，产生正向的创新补偿效应。

(2)环境规制对劳动就业的影响机制。环境规制对劳动就业的影响机制可分为负向的成本效应和正向的替代效应。环境规制可能会增加企业的成本，进一步影响行业内相关产品的市场，在完全竞争行业中，由于产品价格给定，行业内不同的企业成本结构各不相同，即使受到环境规制的强度是相同的，也可能迫使一些边际成本高的企业由于无法承受额外的治污成本压力而关闭生产，从而退出该行业，这会导致整个行业产量的下降和规模的缩小，最终降低了该行业的就业吸纳水平，即负向的成本效应。同时，无论是选择生产末端治理，还是改进生产过程清洁技术，受到环境规制的企业均需增加与清洁治理活动相匹配的劳动力投入，从而增加劳动就业需求，即正向的替代效应，此外，当企业治污技术越倾向于使用劳动力要素时，替代效应越强。

(3)技术创新对劳动就业的影响机制。技术创新对劳动就业产生的影响机制主要是负向的替代效应和正向的补偿效应。技术创新会提高行业的劳动生产率，在行业生产规模没有扩张的前提下，利用机器代替工人，减少对劳动力的需求，而另一方面使得传统部门衰退、产生新兴部门，原有传统部门中的劳动者技能与新兴部门要求的不匹配，引起结构性矛盾，从而使就业人数整体减少，即负向的替代效应。相反地，技术创新的提升大幅度降低了企业生产产品的成本，由于价格优势和新产品的吸引力，产品需求不断扩大，为了满足市场的需求，生产这些产品则需要更多的劳动力，就业需求增长，表现为正向的补偿效应。

2. 数理模型推导

(1)假设国民经济有I个行业，每个行业设定为i,Yit代表t年份行业i的产出，借鉴斯托基(Stokey)的处理方法[27]，将环境污染强度作为环境要素引入生产函数当中，则Yit生产函数中投入要素包括劳动力要素Lit、资本要素Kit、技术要素Ait、环境要素EPit，其中，劳动、资本和环境要素的弹性系数分别为α，β,γ。

(2)假设环境规制强度越大，所需投入的环境治理费用越高，单位污染排放量的治理成本越高。

(3)假设行业代表性企业的生产函数为C-D函数形式。

(4)假设pit代表i行业第t年代表性企业产品价格，wit、rit分别代表劳动力工资和资本利息，θit代表环境成本。

根据上述假设，行业代表性企业的生产函数为：

Yit=Aitf(Lit,Kit，EPit)=Ait(Lit)α(Kit)β(EPit)γ

(1)

利润函数为：

πit=pitAitf(Lit，Kit，EPit)-witLit-ritKit-θitEPit

(2)

代表性企业利润最大化需要满足如下条件：

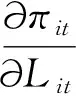
(3)

对方程等式两边求Lit的偏微分如下：

(4)

(5)

将上式简化可以得到：

lnLit=λ0+λ1lnAit+λ2lnEPit+λ3Xit+εit

(6)

其中，λ0、λ1、λ2、λ3分别为常数项和系数。方程(6)表明，环境规制、技术创新与就业增长之间存在一定的内在联系。因此本文试图采用面板向量自回归模型来揭示三者的作用机制。

四、模型设定与数据说明

1．面板向量自回归模型

本文采用面板向量自回归模型(简称PVAR模型)来模拟环境规制、技术创新和劳动就业之间的动态关系。PVAR模型能够解决变量内生性问题，将时间序列中的VAR模型和面板数据相结合，通过广义矩估计、脉冲响应函数以及方差分解分析各个变量间的相互作用。为了将环境规制、技术创新和行业就业效应纳入一个系统框架内考察它们之间的动态关联和变量之间的冲击效应，本文建立的模型如下：

(7)

将yit展开得到下面的公式：

(8)

其中，yit表示第i个行业在第t年由内生变量组成的向量，分别为就业增长、环境规制和研发投入，下标i=(1,2，…，34)表示34个工业行业，t表示2007—2015年，j代表变量的滞后阶数，yt-j代表所有的内生变量，α0代表截距，Aj代表回归系数矩阵，fi和di分别表示固定效应和时间效应，εit表示随机扰动项。本文所使用程序来自连玉君完善后的PVAR2程序(1)世界银行的洛夫(Love)2000年利用PVAR模型对公司财务问题进行了研究，公布了其编写的PVAR模型的Stata程序代码。后来，连玉君在洛夫的程序代码基础上进一步优化和改善，最终形成了比较完善的PVAR程序，称为PVAR2程序包。，使用软件为Stata 11.0。

2．变量说明与数据来源

本文的时间样本区间是2007—2015年，由于国民经济行业分类经过3次调整，我们使用最新版的行业名称进行表述。考虑到数据的完整性，本文删除开采辅助活动、其他采矿业、其他制造业、废弃资源综合利用业、金属制品、机械和设备修理业、水的生产和供应业等数据缺失较多的6个行业，将汽车制造业与铁路、船舶、航空航天和其他运输设备制造业合并为交通运输设备制造业，同时将橡胶制品业与塑料制品业合并为橡胶和塑料制品业，经过以上的处理，得到共计34个工业细分行业。由于不同工业细分行业之间的产品特征不同、生产过程各异，导致工业生产的污染强度和技术水平各不相同，不同污染程度、不同技术水平的行业对环境规制做出的反应不同。因此，我们根据行业污染程度[1]和技术水平[22]的差异对工业行业进行分类(2)行业污染程度的划分结果：清洁行业(17)：石油和天然气开采业，烟草制品业，纺织服装、服饰业，皮革、毛皮、羽毛及其制品和制鞋业，木材加工和木、竹、藤、棕、草制品业，家具制造业，印刷和记录媒介复制业，文教、工美、体育和娱乐用品制造业，医药制造业，橡胶和塑料制品业，金属制品业，通用设备制造业，专用设备制造业，交通运输设备制造业，电气机械和器材制造业，计算机、通信和其他电子设备制造业，仪器仪表制造业。污染密集行业(17)：煤炭开采和洗选业，黑色金属矿采选业，有色金属矿采选业，非金属矿采选业，农副食品加工业，食品制造业，酒、饮料和精制茶制造业，纺织业，造纸及纸制品业，石油加工、炼焦及核燃料加工业，化学原料及化学制品制造业，化学纤维制造业，非金属矿物制品业，黑色金属冶炼和压延加工业，有色金属冶炼和压延加工业，电力、热力生产和供应业，燃气生产和供应业。行业技术水平的划分结果：高技术行业(10)：化学原料及化学制品制造业，医药制造业，化学纤维制造业，金属制品业，通用设备制造业，专用设备制造业，交通运输设备制造业，电气机械和器材制造业，计算机、通信和其他电子设备制造业，仪器仪表制造业。中低技术行业(24)：煤炭开采和洗选业，石油和天然气开采业，黑色金属矿采选业，有色金属矿采选业，非金属矿采选业，农副食品加工业，食品制造业，酒、饮料和精制茶制造业，烟草制品业，纺织业，纺织服装、服饰业，皮革、毛皮、羽毛及其制品和制鞋业，木材加工和木、竹、藤、棕、草制品业，家具制造业，造纸及纸制品业，印刷和记录媒介复制业，文教、工美、体育和娱乐用品制造业，石油加工、炼焦及核燃料加工业，橡胶和塑料制品业，非金属矿物制品业，黑色金属冶炼和压延加工业，有色金属冶炼和压延加工业，电力、热力生产和供应业，燃气生产和供应业。，并在分类的基础上进一步考察三者的关系。

(1)环境规制强度测算。本文借鉴李小平以及秦楠等的做法[28-29]，利用熵值法构建一个环境规制强度的综合指标。选取工业行业废气治理设施运行费用(万元)与废气排放量(亿立方米)的比值、废水治理设施运行费用(万元)与废水排放量(万吨)的比值、固体废弃综合利用率(%)三项指标来对各行业的环境规制强度进行计算。具体计算方法如下。

首先，对三项指标进行无量纲化处理，为了减弱极端值对综合评价的影响，同时消除负值[29]，将坐标平移：

(9)

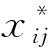
(10)

(11)

其中，各工业细分行业废气排放量、废气治理设施运行费用、废水排放量、废水治理设施运行费用以及固体废弃物综合利用率等数据均来源于《中国环境统计年鉴》。

(2)技术创新的测度(万元)。本文采用各行业的R&D经费作为衡量技术创新的指标[30]，研发投入经费样本数据来源于《中国统计年鉴》。需要注意的是，由于统计口径发生了变化，2010年以前的样本数据为大中型工业企业数据，2011年以后的数据为规模以上工业企业数据，两者数据基本一致。

(3)就业数量的测度(万人)。各工业行业就业总人数用各工业行业全部从业人员年平均人数来衡量，由于年鉴统计口径和指标的变化，2007—2015年就业人数的统计数据来自不同的统计年鉴。其中，2007—2011年规模以上工业企业全部从业人员平均人数数据来源于《中国统计年鉴》，2012年平均就业人员是通过Wind数据库公布的分行业每月从业人员计算得到，2013—2014年的分行业规模以上从业人员平均人数数据来源于《中国工业统计年鉴》。2015年分行业规模以上平均用工人数来源于《中国统计年鉴》。

3．变量描述性统计

各变量的描述性统计结果如表1所示。

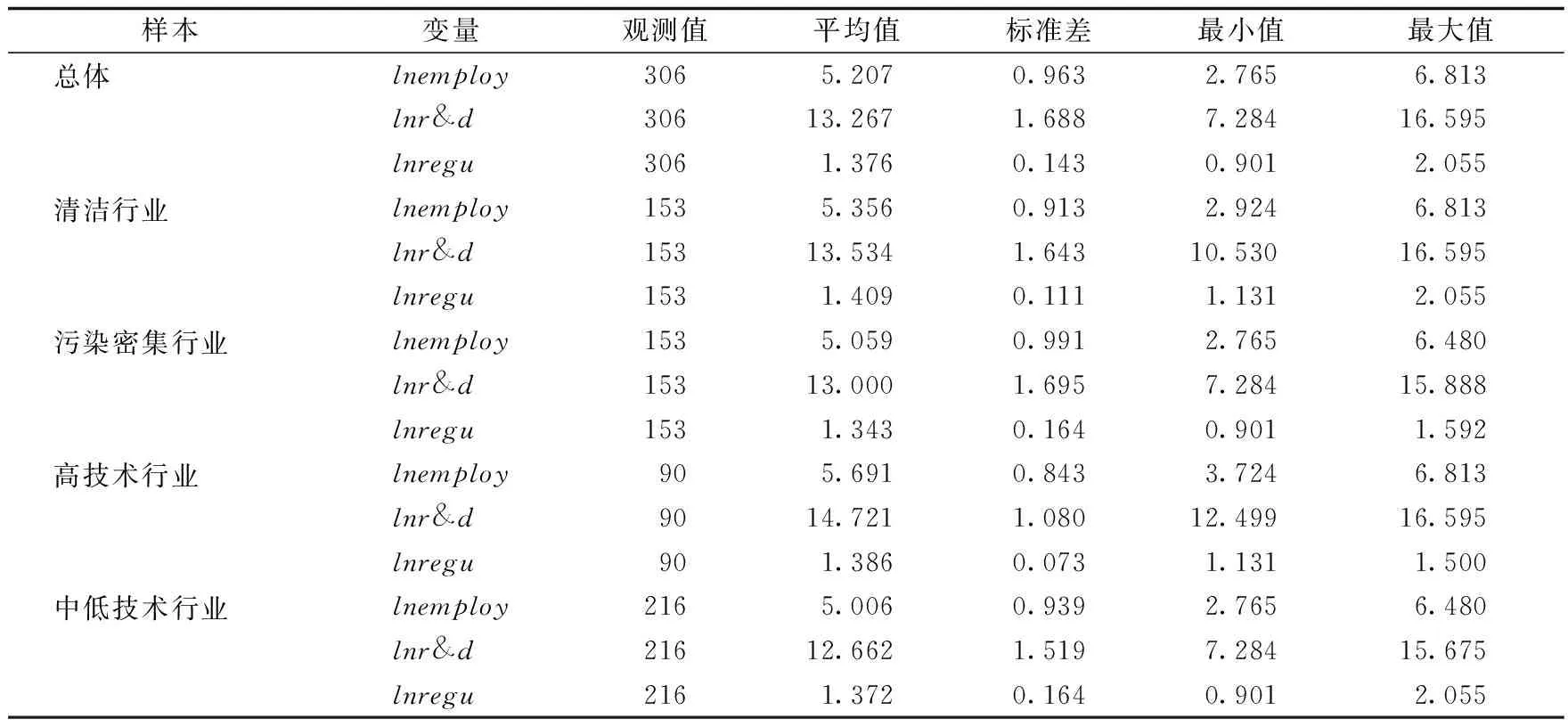
表1 变量统计特征描述

从表1可以看出，34个工业细分行业总体就业水平平均为5.207，最大值为6.813，最小值为0.963，其中，清洁行业就业水平平均为5.356，污染密集行业平均为5.059，高技术行业平均为5.691，中低技术行业平均为5.006。整体的技术创新水平为13.267，其中，清洁行业均值为13.534，污染密集行业均值为13.000，高技术行业均值为14.721，中低技术行业均值为12.662。环境规制强度均值为1.376，其他行业依次为1.409、1.343、1.386、1.372。在整个样本研究期内，各个变量的离散程度较高，表明行业之间呈现出一定的异质性。

五、实证结果及分析

1．单位根检验与协整检验

在进行PVAR模型估计前，采用LLC和 ADF-Fisher检验三个变量的平稳性，从表2可以看出，三个变量的一阶差分是平稳的，即同阶单整，满足协整分析的条件。

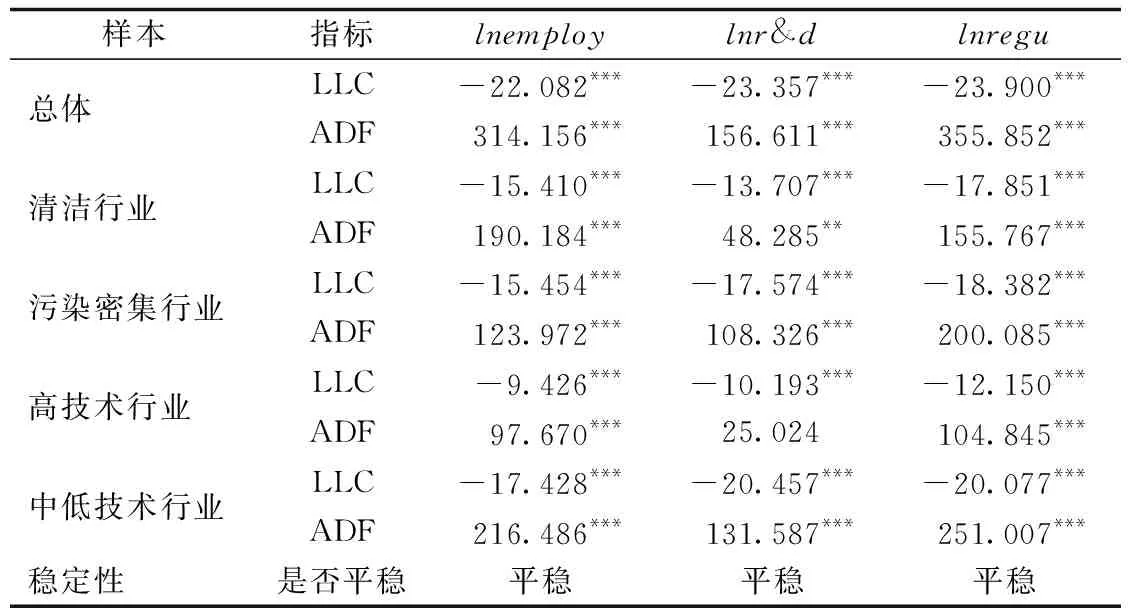
表2 单位根检验结果

注：***、**、*分别表示在1%、5%、10%的置信水平上显著。

然后，通过面板协整检验考察环境规制、技术创新和经济增长的长期均衡关系，构造了四个统计量：两个组统计量Gt和Ga，两个面板统计量Pt和Pa，每组统计量的区别在于是否考虑了序列相关。组统计量Gt原假设为不存在协整关系，Ga原假设为至少存在一组协整关系；面板统计量Pt原假设为不存在协整关系，Pa的原假设为面板整体上存在协整关系。从表3中四个统计量我们可以看出：至少存在两个统计量显著拒绝原假设，因此认为环境规制、技术创新与劳动就业之间存在长期协整关系。

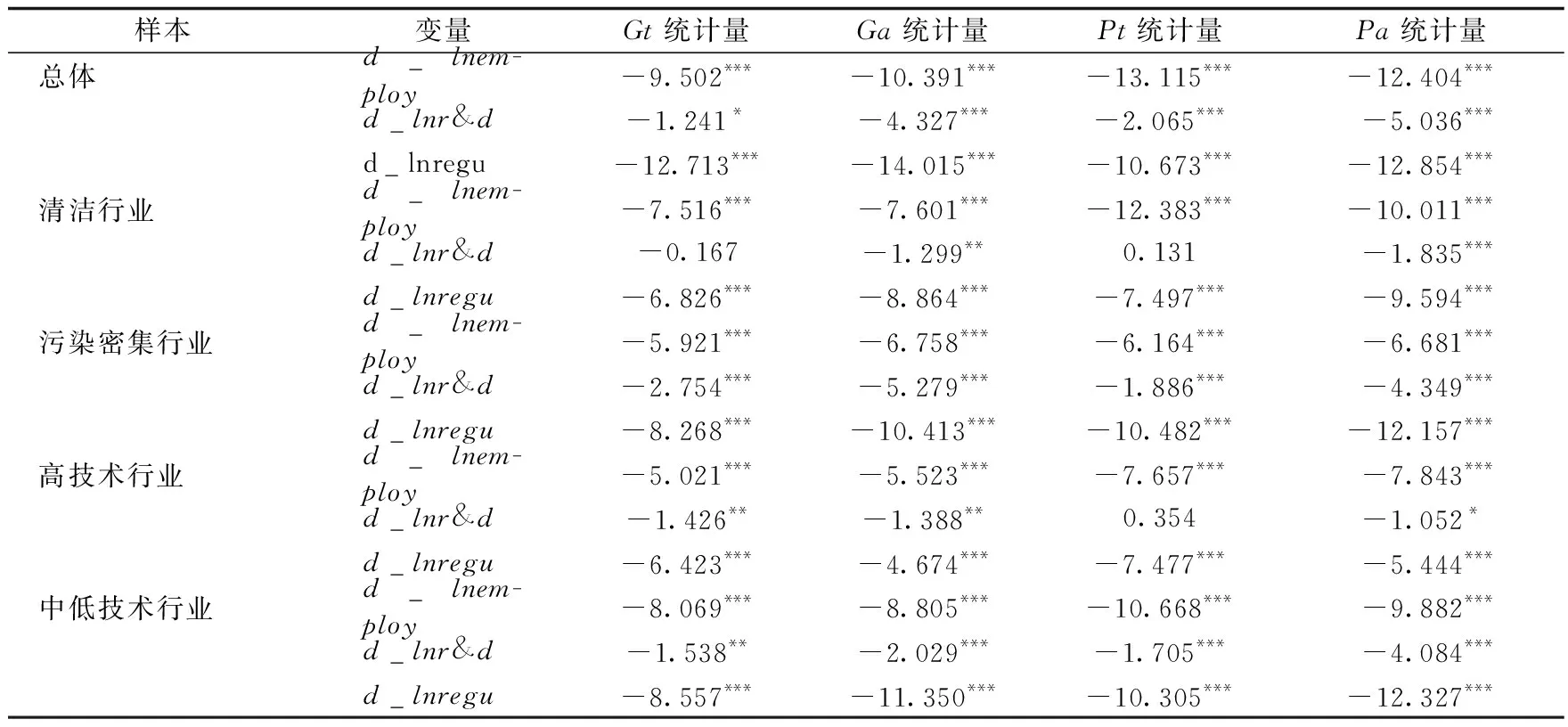
表3 面板协整检验结果

注：***、**、*分别表示在1%、5%、10%的置信水平上显著。

2．模型的GMM估计

根据相关准则判断模型的最佳滞后阶数为3阶，此时模型具有较好的估计结果。采用向前差分对固定效应进行消除，对34个工业行业的GMM估计结果(见表4)表明，环境规制、技术创新和劳动就业之间的动态影响关系存在行业异质性。

从劳动就业方程可以看出，整体上技术创新对劳动就业的影响在前期为负，后期为正，清洁行业和高技术行业两者关系呈现倒“N”型关系，污染密集行业技术创新与就业呈现“U”型关系，中低技术行业技术创新对就业的影响三期都为正。整体上环境规制与就业之间呈现“U”型关系(包括清洁行业、高技术行业和中低技术行业)，污染密集行业环境规制对滞后期就业的影响都为正。由此说明，从长期来看，技术创新对就业的影响主要表现为创造效应，并且在不同行业存在异质性。同时，政府环境管制对就业的长期影响也为正，一定程度上解释了双重红利假说。

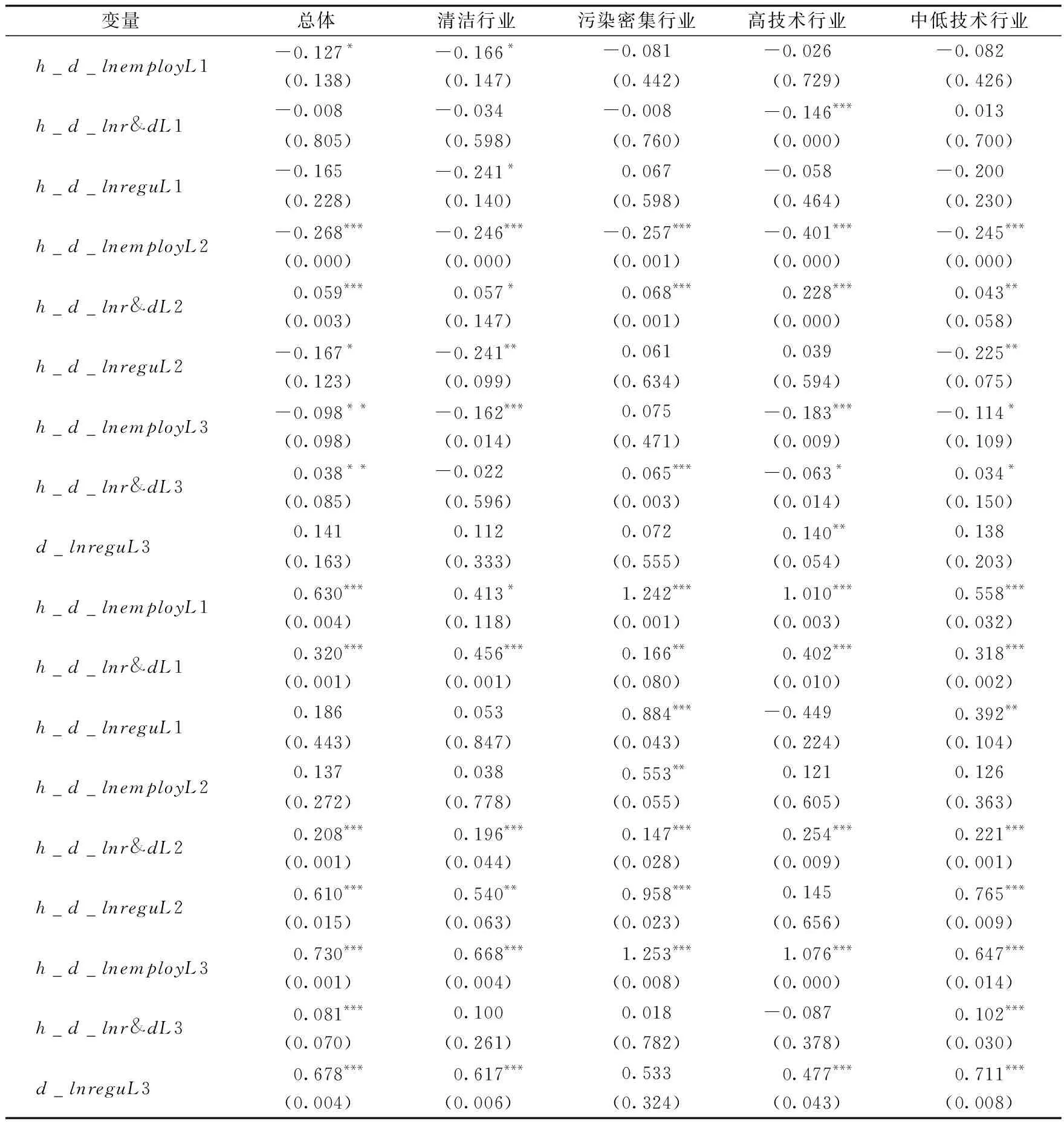
表4 模型的GMM估计结果

注：1.h_表示经过前向均值差分处理后的变量，L1表示时滞yt-1；2.***、**、*分别表示在1%、5%、10%的置信水平上显著；3.括号中为标准误。

从技术创新方程可以看出，环境规制对技术创新的影响为正(高技术行业为“U”型关系)，污染密集行业环境规制对技术创新的正向作用比清洁行业更明显，中低技术行业环境规制对技术创新的正效应比高技术行业要大。整体上验证了弱波特假说的存在，其中污染密集行业和中低技术行业受到的冲击更大，这说明目前环境政策具有一定的合理性，环境规制对于污染密集行业的技术创新起到了激励作用。

环境规制方程显示技术创新和劳动就业对环境规制的解释能力并不强(回归系数不显著，没有附在表中)。因此，本文重点关注环境规制对技术创新的动态影响、环境规制对劳动就业的动态影响以及技术创新对劳动就业的动态影响。接下来利用脉冲响应函数和方差分解等计量工具对上述经济变量之间的动态关系进一步考察。

3．脉冲响应分析

(1)工业行业整体脉冲响应图分析。由图2可以看出，①a表示，环境规制对技术创新的正向影响先变大再变小，呈现上下波动的趋势。②b表示，环境规制对劳动就业的影响由负变为正，最终趋向于零。③c表示，技术创新对劳动就业的正向作用由零逐渐变大再降为零，呈现周期性波动，幅度越来越小。可知，工业行业环境规制对技术创新的冲击为正，环境规制对劳动就业的冲击先负后正，技术创新对劳动就业的冲击为正。

图2 工业行业脉冲响应图

(2)清洁行业脉冲响应图分析。由图3可以看出，①a表示，环境规制对技术创新的影响都为正，正向作用最大达到0.05左右。②b表示，环境规制对于劳动就业的负向作用比整体的要大，正向效应差别不大。③c表示，不同于整体行业，清洁行业技术创新对劳动就业的影响第一期为负，第二期为正，第三、四期为负，第五期趋向于零。可知，清洁行业环境规制对技术创新的冲击为正，环境规制对劳动就业的冲击先负后正，技术创新对劳动就业的冲击呈现“负-正-负-零”波动。

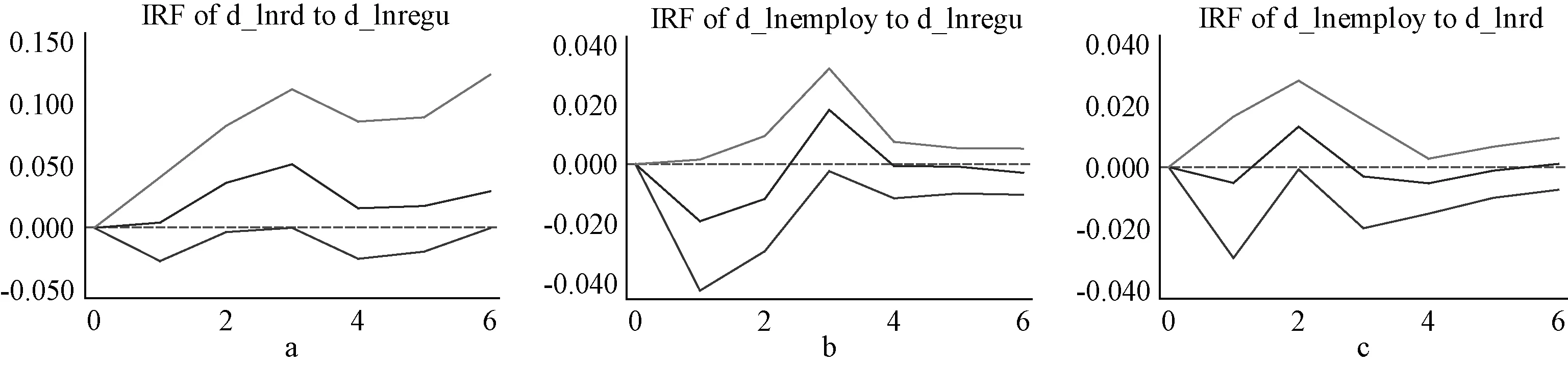
图3 清洁行业脉冲响应图

(3)污染密集行业脉冲响应图分析。由图4可以看出，①a表示，环境规制对技术创新的影响都为正，正向作用最大达到0.04左右。②b表示，污染密集行业环境规制对于劳动就业呈现微弱的正向作用。③c表示，不同于整体行业和清洁行业，污染密集行业技术创新对劳动就业的影响第一期为负，第二、三期为正，第四期为负，第五、六期为正，正向作用持续时间更长。可知，污染密集行业环境规制对技术创新的冲击为正，环境规制对劳动就业的冲击表现为微弱的正向作用，技术创新对劳动就业的冲击呈现“负-正-负-正”波动，从长期来看具有潜在的正向效应。

图4 污染密集行业脉冲响应图

通过对比分析清洁行业和污染密集行业，可以看到环境规制对技术创新都存在正向作用，表现为环境规制的创新补偿效应。环境规制对污染密集行业就业存在微小的积极作用，对清洁行业就业的滞后1期为负，滞后3期为正，这可能是因为污染密集行业环境规制对就业的正向替代效应略大于成本效应，清洁行业在滞后1期负向的成本效应大于替代效应，在滞后3期成本效应减小。技术创新对污染密集行业就业的滞后2—3期都为正，对清洁行业就业的滞后2期为正，污染密集行业技术创新对就业的正向作用比清洁行业持续时间更长。技术创新对就业的影响在初期主要表现为替代效应，在后期主要表现为正向的补偿效应。

(4)高技术行业脉冲响应图分析。由图5可以看出，①a表示，环境规制对技术创新的影响第一期为负，后面都为正，正向作用最大达到0.025左右。②b表示，高技术行业环境规制对于劳动就业呈现微弱的正负上下波动作用，直到第六期趋于收敛。③c表示，不同于整体行业，高技术行业技术创新对劳动就业的影响第一期为负，第二、三期为正，正向作用最大为0.02左右，第四期为负，第五期趋向于零。可知，高技术行业环境规制对技术创新的先负后正，环境规制对劳动就业的冲击表现为“负-正-负-正”波动，技术创新对劳动就业的冲击呈现“负-正-负-零”波动，类似于清洁行业。

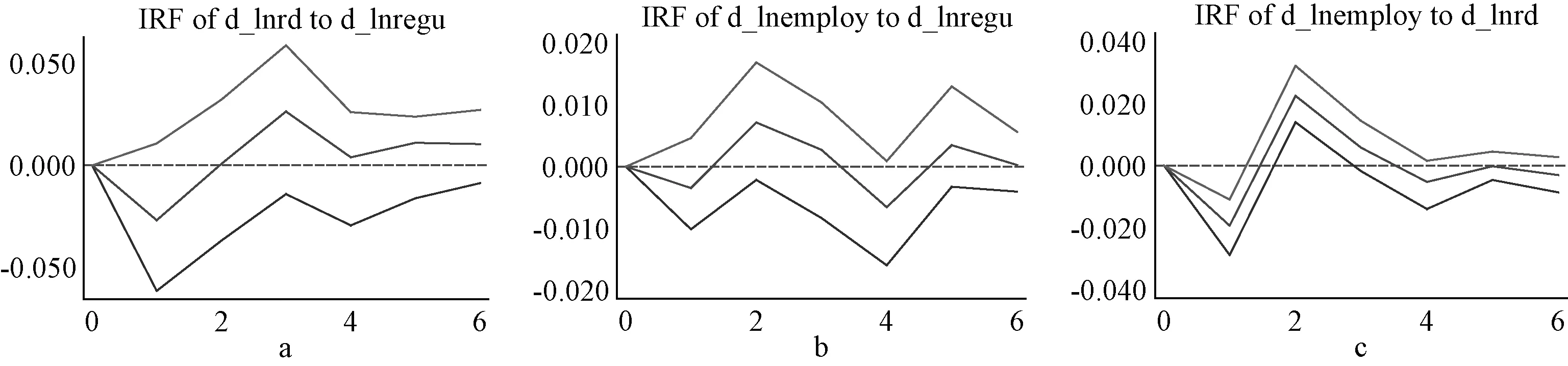
图5 高技术行业脉冲响应图

(5)中低技术行业脉冲响应图分析。由图6可以看出，①a表示，环境规制对技术创新的影响都为正，正向作用最大达到0.04左右。②b表示，中低技术行业环境规制对于劳动就业的影响先为负，再为正，到第六期趋于收敛。③c表示，不同于整体行业和高技术行业，中低技术行业技术创新对劳动就业的正向作用由零逐渐变大再降为零，呈现短期周期性波动，幅度越来越小。可知，中低技术行业环境规制对技术创新的影响为正，环境规制对劳动就业的冲击表现为“负-正-零”波动，技术创新对劳动就业的冲击呈现正向影响。

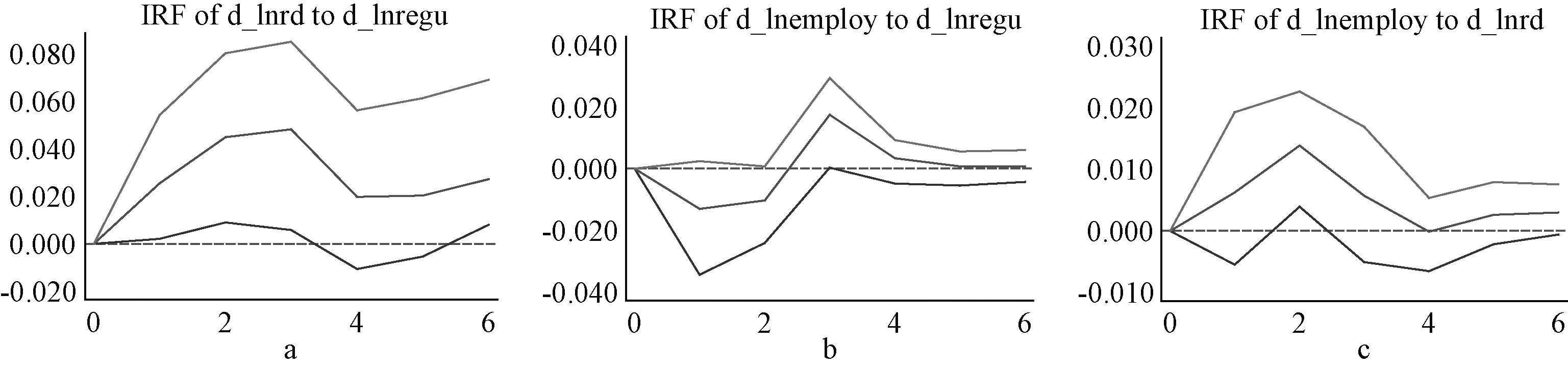
图6 中低技术行业脉冲响应图

经过对比发现，在高技术行业环境规制对技术创新的滞后1期为负，滞后3期为正，但在中低技术行业滞后1—3期都表现为正。在高技术行业，开始环境规制对技术创新的补偿效应小于抵消效应，后期抵消效应减小。这可能是因为高技术行业通过改变生产技术遵循环境规制的边际成本较大。在中低技术行业，补偿效应大于抵消效应，环境规制对创新资金的挤出较少。相同的是，在两类行业环境规制对就业的影响都是先负后正的“U”型关系。技术创新对高技术行业的就业效应表现为滞后1期为负，滞后3期为正，对中低技术行业表现为持续的正向影响。高技术行业的技术创新产生的替代效应较大，且大于补偿效应，中低技术行业产生的替代效应较小。

4.方差分解分析

通过方差分解可以进一步度量环境规制、技术创新和劳动就业之间的长期动态关系，分析各变量的方差贡献率构成。

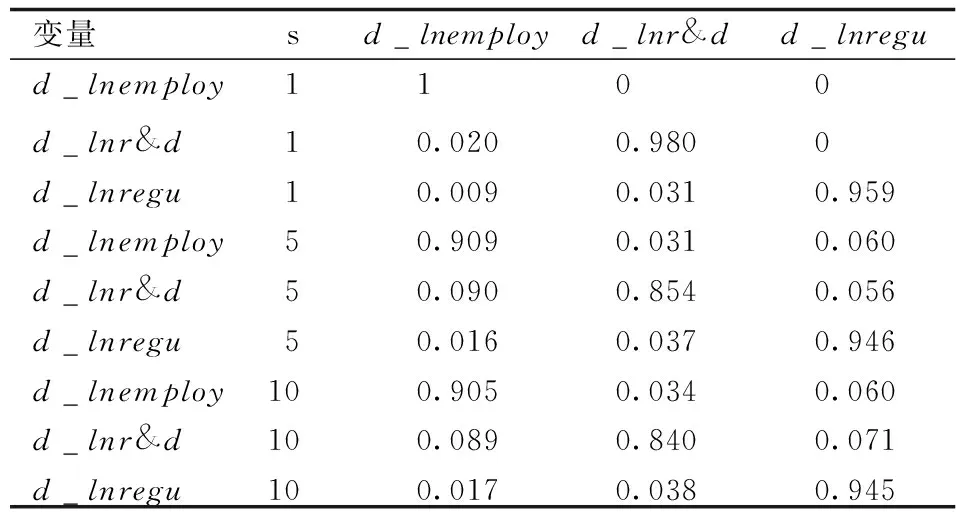
表5 整体方差分解

由表5可以看出，第10期与第5期的方差分解结果基本相同，这表明第10期后每一种冲击对某一变量变动的解释力度非常稳定。结果表明，整体上环境规制对劳动就业的贡献度为6.0%，技术创新对劳动就业的贡献度为3.4%，环境规制对技术创新的贡献度为7.1%。

表6中，清洁行业和污染密集行业的方差分解，结果表明环境规制对劳动就业的贡献度分别为8.9%、1.5%，技术创新对劳动就业的贡献度分别为2.5%、8.2%，环境规制对技术创新的贡献度分别为6.9%、10.1%。其中，清洁行业的就业受环境规制方差贡献大于污染密集行业，污染密集行业的就业受技术创新方差贡献大于清洁行业，污染密集行业的技术创新受环境规制方差贡献也大于清洁行业。

通过表7中高技术行业和中低技术行业的方差分解对比发现，环境规制对劳动就业的贡献度为5.1%、7.4%，技术创新对劳动就业的贡献度为38.8%、3.6%，环境规制对技术创新的贡献度为6.2%、9.7%。其中，中低技术行业的就业受环境规制的方差贡献大于高技术行业，高技术行业的就业受技术创新的方差贡献大于中低技术行业，中低技术行业的技术创新受环境规制方差贡献大于高技术行业。由此可见，高技术行业的技术创新有助于带动高质量就业。

5.稳健性检验

利用创新的产出指标发明专利申请数替代之前创新的投入指标研发投入经费对就业效应的稳定性进行检验。结果表明，单位根检验、脉冲响应函数分析和方差分解结果基本一致，详见表8。表明本文的研究结论比较稳定。

六、 结论及启示

1．研究结论

本文将环境要素引入道格拉斯生产函数，分析环境规制和技术创新对劳动就业的影响机制，选取2007—2015年中国34个工业细分行业的面板数据，采用PVAR模型考察环境规制、技术创新和劳动就业三者的动态关系，得到了如下结论。

(1)环境规制的动态创新效应。从整体上看，环境规制与技术创新呈现正向关系，环境规制对技术创新的补偿效应大于抵消效应。其中，高技术行业表现为先负后正再负的影响，其他分类行业都表现为正向关系。对于环境规制产生的冲击，清洁行业比污染密集行业的技术创新正向波动更大，但是污染密集行业技术创新受环境规制方差贡献更高，绿色技术创新能力的提升存在较大潜力；高技术行业的技术创新反应刚开始为负，后期为正，整体上比中低技术行业的正向幅度要小，技术创新受环境规制方差贡献更小。环境规制对技术创新的正向作用在中低技术行业、污染密集行业和清洁行业都比较明显，一定程度上验证了弱波特假说。因此，污染密集行业和中低技术行业的环境规制强度可以进一步增加。

表8 稳健性检验结果

注：1.h_表示经过前向均值差分处理后的变量，L1表示时滞yt-1；2.***、***分别表示在1%、5%、10%的置信水平上显著；3.括号内为标准误。

(2)环境规制的动态就业效应。从整体上看，环境规制与劳动就业呈现“U”型关系，越过曲线的最低点以后，替代效应大于成本效应。其中，污染密集行业环境规制对滞后期就业的影响都为正，其他分类行业都是先负后正的“U”型关系。对于环境规制产生的冲击，清洁行业比污染密集行业的就业反应更为明显，清洁行业的就业响应先为负，后面为正，并且幅度较大，而污染密集行业的就业响应呈现微弱的正向趋势，清洁行业的就业受环境规制的方差贡献比污染密集行业要高，但污染密集行业正向作用更持久。相对于高技术行业，中低技术行业的就业响应先向下后向上波动的周期更长，幅度更大，中低技术行业的就业受环境规制方差贡献比高技术行业要高。依据污染程度分行业来看，污染密集行业的曲线位于清洁行业的下方，这说明污染密集行业需要更高的环境规制强度，如此才能实现同样的就业效果。依据技术水平分行业来看，环境规制对中低技术行业的冲击更大，因此有必要通过提高中低技术行业的环境规制程度强化其对就业产生的积极作用。

(3)技术创新的动态就业效应。从整体上看，技术创新与劳动就业呈现“U”型关系，在后期，技术创新的补偿效应逐渐抵消其替代效应。中低技术行业环境规制对滞后期就业的影响都为正，其他分类行业都是先负后正的波动关系。对于技术创新产生的冲击，污染密集行业比清洁行业正向响应的时间更长，就业受技术创新方差贡献比清洁行业大。而高技术行业的反应先负后正，波动幅度较大，中低技术行业从零到正向波动，幅度相对较小，高技术行业的就业受技术创新方差贡献要比中低技术行业大得多。依据技术水平来看，高技术行业的曲线位于中低技术行业的上方，就业破坏和就业创造都更大，因此应当发挥高技术企业的就业创造效应，避免其破坏效应，同时，应当提高中低技术企业的研发能力，在维持就业稳定的同时实现就业结构优化。依据污染程度分行业来看，技术创新对污染密集行业的冲击更大，加快污染密集行业的技术升级，对于实现产业升级和稳定就业具有积极作用。

2．启示

随着经济全球化以及各种环境问题、社会问题的凸显，中国同时面临环境规制强度较低、基础创新能力不足、失业率居高不下等多重问题，如何实现经济、生态和民生协调发展是我们必须面对的重要议题。本文的主要贡献在于通过考察环境规制、技术创新与劳动就业之间的动态关系及其行业异质性，检验环境规制和技术创新对工业行业就业水平的影响，为政府针对不同行业制定差异化的政策提供理论参考。现阶段应该加强环境规制力度，加大研发投入，提高原始创新能力，扩大生产规模，吸纳更多的绿色就业。

(1)制定适合行业发展的环境规制政策。制定适当的环境规制政策能够激励企业进行技术创新，最大限度地发挥环境规制的弱波特效应，提高企业的治污能力。对于污染密集行业和中低技术行业采取命令控制型环境规制工具，对于清洁行业和高技术行业可以采用激励型环境规制工具。

(2)加大研发资金的投入力度，提高行业绿色创新水平，支持能源节约型和高新技术产业发展。针对环境规制会挤占企业研发资金，政府应该为积极进行绿色技术创新的企业提供更多的资金支持和政策扶持，实施绿色创新战略，促进工业经济与环境协调发展。

(3)鼓励绿色转型，提倡绿色就业。2018年《世界劳工报告》指出，如果采取适当政策促进绿色经济的发展，到2030年，绿色经济将在全世界创造2400万个就业机会。绿色经济将为全球创造就业机会，同样，绿色就业也会促进经济可持续发展。因此，中国实现可持续发展目标有赖于全部门的绿色就业推动。