风洞模型加速度负反馈振动主动控制方法研究
2020-06-17温正权周孟德姚壮唐琳琳王琴琴刘巍
温正权,周孟德,姚壮,唐琳琳,王琴琴,刘巍
(大连理工大学,辽宁大连116024)
0 引言
利用尾撑式风洞模型进行风洞试验时,由于系统的低阻尼特性,在宽频变气动载荷干扰下容易激发风洞飞行器缩比模型的多阶模态振动。该类大幅振动导致风洞试验数据不稳定,不仅影响数据质量和测试精度,限制测试包线范围,甚至会导致测力天平过载,严重影响风洞试验的可靠性和安全性[1-2]。因此,风洞模型振动控制技术的研究具有重要的意义和应用价值。
主动振动控制方法具有适应性强、响应速度快、抑振效果好的特点,相关研究机构针对风洞模型振动问题在主动振动控制系统结构设计和振动主动控制算法等方面进行了研究。ViGYAN Inc.的S.Balakrishna等人和 NASA Langley Research Center的 W.A.Kilgore等人以叠堆式压电陶瓷作为阻尼器,针对探路者一号模型设计了阻尼器前置减振系统并提高俯仰和偏航主振动模态的对数衰减率近4倍,针对两种运载火箭缩比模型设计了阻尼器后置减振系统并减小俯仰和偏航方向振动幅值60%左右[3];ERAS GmbH的H.Fehren等人和ETW的G.Hefer等人将碳纤维套筒安装在压电陶瓷外部,设计了一种前置减振器使得马赫数为0.77、雷诺数为22×106工况下降低俯仰方向振动幅值近70%[4]。国外研究主要使用测力天平采集俯仰、偏航向力信号,经信号处理得到动载荷信号作为反馈信号以实现振动主动控制[1,3],天平可测振动方向及可测振动位置的灵活性较差,使得控制算法的设计未能充分考虑到各系统特性,另外随模型变化每次接入控制系统的天平也随之变化,增加了算法设计和调试难度,振动控制效果有限。
国内研究机构对该问题的研究虽然起步较晚,但近些年也取得了一些研究成果。南京航空航天大学的陈卫东等人基于俯仰方向放置的加速度计设计了一种安装于模型内部空腔的电磁作动减振系统,通过地面实验仅针对支杆系统俯仰方向一阶模态振动进行了研究[5];沈星等人在支杆尾部下方安装了一对控制俯仰方向振动的压电陶瓷作动器,目前仅针对俯仰方向前两阶模态利用LQR控制算法进行了振动控制[6]。
在加速度负反馈控制器应用研究方面,袁明等人基于加速度负反馈控制器针对铝制柔性板结构利用压电片进行了振动控制研究[7],Ezdiani Talib等人将该控制器应用于两层建筑式框架结构利用线性伺服电机实现了振动主动控制[8]。目前,加速度负反馈控制器仅限于同位配置振动控制的研究。
本文为实现尾撑式风洞模型振动控制设计了加速度负反馈(Negative Acceleration Feedback,简称 NAF)振动主动控制算法。针对尾撑式风洞模型系统,利用ANSYS软件进行计算模态分析并通过地面实验进行试验模态分析。在异位配置NAF控制器基础上结合内嵌压电陶瓷作动器的风洞模型振动主动控制系统设计了分别针对第二阶模态和前二阶模态的单模态NAF控制算法和双模态NAF控制算法。利用锤击实验验证算法的有效性并对比了单模态NAF控制算法和双模态NAF控制算法的实验结果。
1 风洞模型系统及其振动主动控制原理
如图1所示,尾撑式风洞模型系统主要由风洞模型、测力天平、尾撑式支杆及弯刀组成。尾撑式风洞模型系统通过弯刀固支于风洞中,使风洞模型处于风洞界面中心。
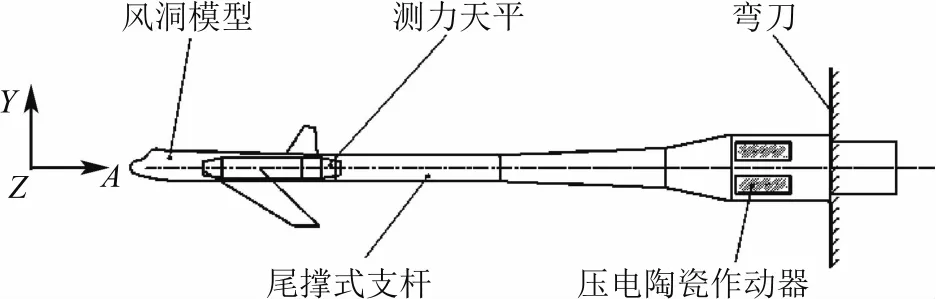
图1 尾撑式风洞模型系统示意图
该结构可视作悬臂结构细长支杆,因此考虑抑振器后置结构[3]。叠堆式压电陶瓷作动器体积小、输出能力高、响应速度快、频响宽[9],基于输出功率、工作频率等特性并结合支杆结构空间,将压电陶瓷作动器内嵌于支杆尾部作为抑振器。
风洞模型振动主动控制系统原理如图2所示,通过振动传感器测量得到由宽频变气动荷载激励的风洞模型振动信号,将该信号输入控制器并通过振动主动控制算法计算得到控制信号,控制信号经功率放大器放大后驱动抑振器轴向(即A方向)伸长,抑振器输出A方向的力对支杆固支端产生反向弯矩作用以抵抗固支端因飞行器模型受风载而导致的弯矩,达到抑制系统振动的目的。

图2 风洞模型振动主动控制系统原理图
2 系统模态分析
2.1 系统计算模态分析
尾撑式风洞模型系统是一个多自由度振动系统,该系统的动力学方程的矩阵形式为
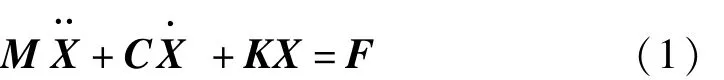
式中:M,C和K分别为质量矩阵、阻尼矩阵和刚度矩阵;X为物理坐标系下的位移向量;F为力向量。
物理坐标系下耦合的动力学方程通过特征值求解得到模态振型矩阵φ,由振型矩阵得到模态转换方程,将物理坐标系下动力学方程转换到模态空间下动力学方程。
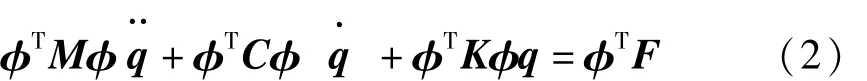
式中:φ为模态振型矩阵;q为模态坐标列向量。
根据模态空间理论,每阶模态与其他阶模态都线性独立,总响应是参与系统响应的所有模态的线性组合[10-11]。模态振型矩阵 φ不为时间函数,因此满足

式中:qk为第k阶模态坐标向量。
模态阶数越低、响应越大,越容易对实际结构产生危害[10-11],低阶振动模态是引起结构大幅剧烈振动的主要原因,因此关心结构低阶振动模态以减小控制成本并简化控制结构复杂性。利用ANSYS有限元软件对系统结构进行计算模态分析,结果如图3所示。

图3 尾撑式风洞模型系统结构计算模态分析结果
该系统低阶模态具有强方向性,第一、三阶模态为Z向振动,第二、四阶模态为Y向振动,因此系统偏航方向固有振动模态不容忽视[12]。如图4所示的抑振器(P1~P4)正方形布局可提高系统Y,Z向抗弯系数[3]。该布局方案下抑振器可控振动方向为YP,ZP向,根据固有模态一般正交性,YP,ZP向振动是所有振动模态在该方向上的叠加,即抑振器具有结构耦合性。因此采用正方形布局使单个抑振器可对多阶模态振动产生作用。
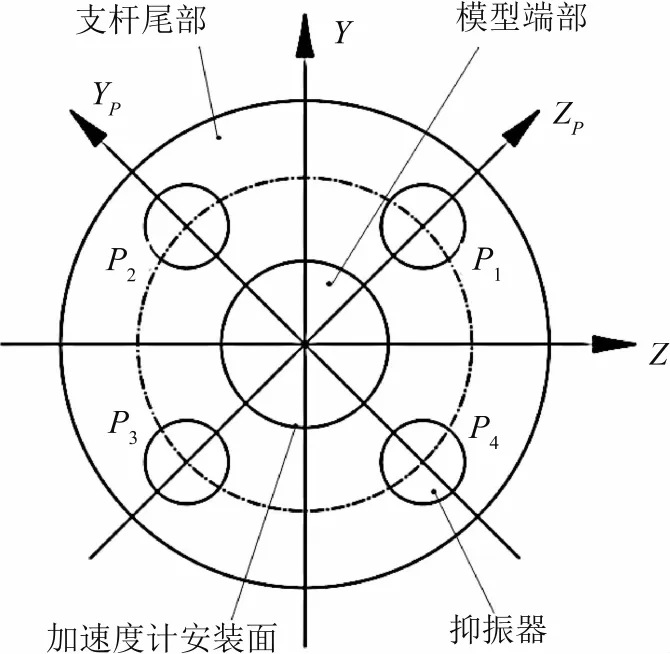
图4 抑振器布局图
2.2 系统试验模态分析
根据计算模态分析结果,尾撑式风洞模型系统可近似为一个悬臂杆结构,该结构自由端即飞行器模型端部振型值显著且不是模态节点,可作为模态参考点。由于该结构低阶模态具有强方向性且主要振动方向为Y,Z向,选用两个单轴加速度计分别安装在飞行器模型端部Y,Z向外表面,通过锤击法对该结构进行模态识别测量。实测结果如表1所示,系统第一、二阶固有频率接近,第三、四阶固有频率接近。系统试验模态分析结果与仿真分析结果的振动自由度方向相一致、固有频率趋势也大致相同,一定程度验证了仿真结果的有效性。由于计算模态分析和试验模态分析中所采用的边界条件、零件配合等方面存在一定的差别,且高阶的模态受外界干扰因素的影响较大,导致所分析的第四阶模态频率仿真结果与试验结果存在较大的误差。
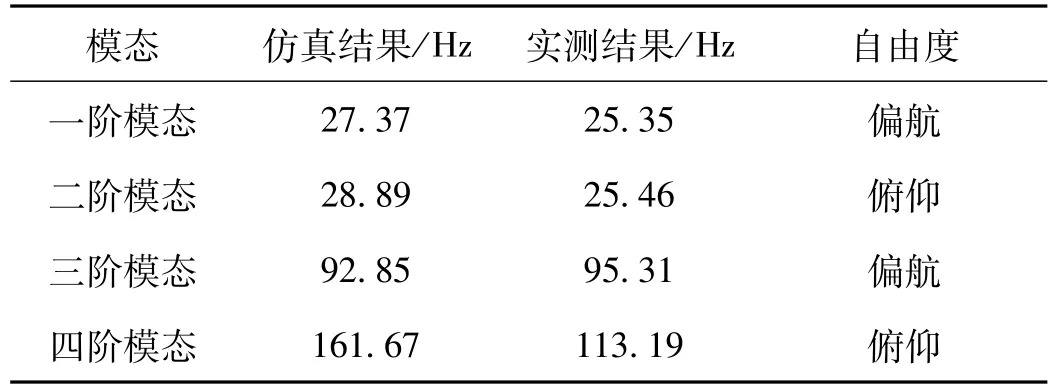
表1 计算模态分析与试验模态分析结果对比
3 控制器设计
3.1 加速度负反馈控制器原理
加速度计频响范围宽、线性度好、信噪比高,可直接准确获取因动载荷导致的振动信号且不干扰测力天平数据采集,选用安装灵活并可连长导线使用的ICP型单轴加速度计作为振动主动控制系统的振动传感器。
加速度传感器测量得到的加速度信号不经过数值积分、去直流偏置等信号处理过程,直接利用该信号作为振动控制系统输入信号的控制算法称为加速度负反馈振动主动控制算法(简称NAF控制器)[7-8]。NAF控制器可避免加速度信号积分、高频噪声等信噪比影响因素对控制系统鲁棒性造成干扰。基于单自由度振动系统的NAF控制器原理图如图5所示。
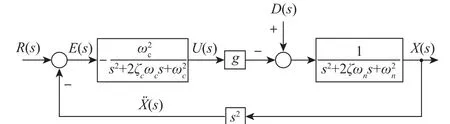
图5 加速度负反馈控制器原理图
假设受控单自由度振动系统结构运动方程为
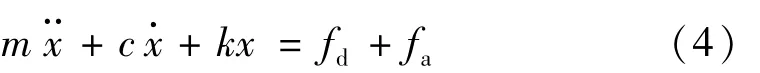
式中:m,c和k分别为系统质量、阻尼和刚度系数;x为物理坐标系下位移;fd为外界激励力;fa为抑振器输出力,fa=-mgu;g为控制器增益;u为控制信号。
NAF控制器方程可写作
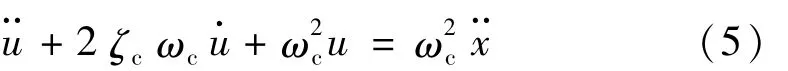
式中:ζc为控制器阻尼比;ωc为控制器固有频率。
根据式(5),NAF控制器传递函数为
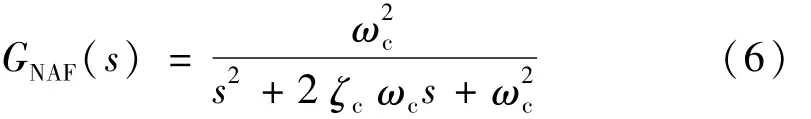
根据图5,整个系统传递函数为

控制系统为离散控制系统,由于特定频域有重要动态特性且为避免频率混叠,采用双线性变换将式(6)的连续系统离散化,可得到
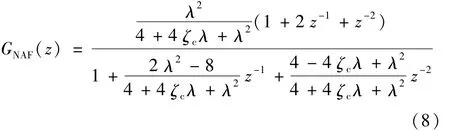
式中:λ=ωcT,T为采样时间。
为保证系统的可观性和可控性,传感器和抑振器无法避免异位配置即控制系统为非最小相位系统。而NAF控制器适用于同位配置,需补偿由于异位配置等因素导致的控制系统的输入时滞。可利用状态预估法对该时滞量进行补偿,假设(t-τ)时刻系统状态量为
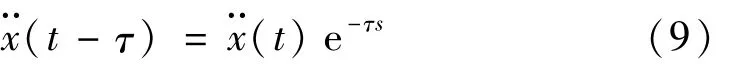
式中:x¨(t)为加速度状态量;τ为时滞量。
将 x¨(t-τ)eτs按泰勒级数展开并忽略高阶项可用来估计 t时刻的系统状态 x¨(t)为
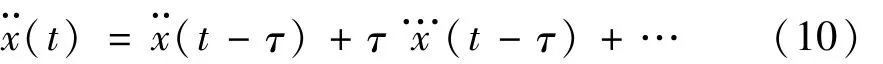
3.2 单模态加速度负反馈控制算法
NAF控制器针对单一模态振动控制[7],将基于NAF控制器并只针对风洞试验主振动模态即系统第二阶振动模态的控制算法称为单模态NAF控制算法。该算法采用安装于风洞模型端部Y向负半轴加速度计采集的加速度信号作为控制系统反馈信号,Z向加速度计只作为观测器。为使Y向输出弯矩最大,将抑振器沿Z轴分成两组,即P1和P2为A组、P3和P4为B组。
其原理如图6所示,利用带通滤波器对低频衰减严重、高频非线性严重的Y向加速度信号进行信号处理得到具有时滞量为τ的物理坐标系下第二阶模态时域信号x¨2(t-τ),将经状态预估时滞补偿器补偿后的信号输入NAF控制器得到控制信号u(t)。方向判断器和限幅器配合保证给抑振器输出的控制电压V(t)为正。当外部激励对系统产生+Z向弯矩时,系统由于阻尼作用趋于平衡位置即经加速度计采得信号为负,应给B组抑振器输出正向电压使其伸长产生抵抗弯矩。
3.3 双模态加速度负反馈控制算法
尾撑式风洞模型振动主动控制系统内在模态解耦,抑振器布局形式使得外在输入控制耦合。考虑抑振器可控振动方向为YP,ZP向,通过在风洞模型端部YP,ZP向负半轴分别安装一个单轴加速度计直接测量抑振器向振动信号。由于系统极点全局特性,抑振器向前两阶振动模态接近,叠加后的信号可近似认为特定单一模态,满足NAF控制器适用条件。
将基于NAF控制器并针对风洞模型前两阶振动模态的控制算法称为双模态NAF控制算法。通过两个单轴加速度计测量并经数字信号处理得到前两阶模态在ZP,YP向叠加后的无时滞时域信号,各通过一个NAF控制器计算得到控制信号分别用于控制P1,P3和P2,P4。
各压电陶瓷的控制电压为
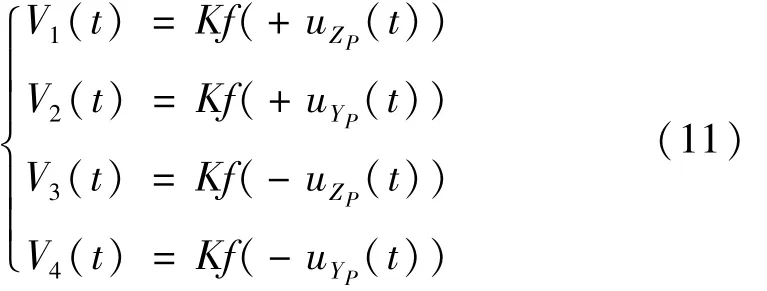
式中:Vi(t)为各压电陶瓷控制电压;uYP(t),uZP(t)为YP,ZP向控制信号;K为功率放大器电压放大倍数;最高工作电压。
4 实验验证
4.1 实验装置及系统
搭建如图7所示的风洞模型振动主动控制系统实验平台。风洞试验条件下宽频变气动载荷激发系统多阶振动模态,地面实验中可通过宽带激励方式即锤击实验激发系统多阶模态振动。通过锤击系统主要振动方向即Y,Z向,从时、频域比较单模态NAF控制、双模态NAF控制的振动抑制效果。

图7 风洞模型振动主动控制系统实验平台
4.2 实验结果分析
锤击偏航(+Z)方向主要激起第一阶振动模态,锤击俯仰(-Y)方向主要激起第二阶振动模态,因此针对主要激励模态对各次锤击实验结果进行分析。锤击实验的时域、频域响应结果分别如图8、图9所示,将实验结果的镇定时间和阻尼比汇总如表2所示。

图8 锤击实验时域响应结果
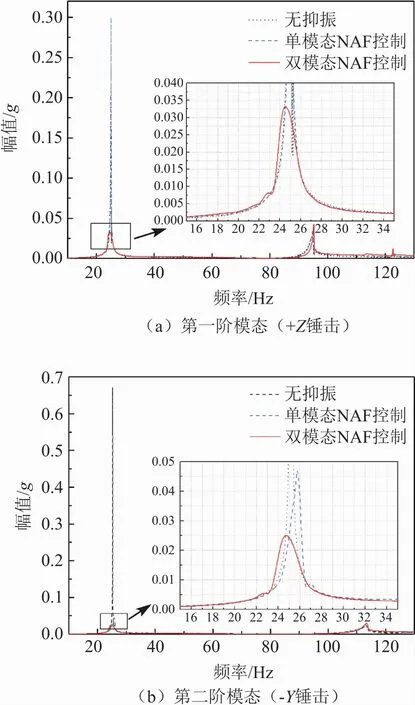
图9 锤击实验频域响应结果
单模态NAF控制有效控制系统第二阶模态振动,将第二阶模态阻尼比提高16.1倍,镇定时间缩短24.68 s,证明了NAF控制器有效性。双模态NAF控制有效抑制系统前两阶模态振动,单模态NAF控制对第一阶模态振动控制失效。针对第二阶振动模态,双模态NAF控制效果优于单模态NAF控制。从整体控制效果看,双模态NAF控制效果较好,将前两阶模态阻尼比分别提高至0.0307,0.0350,镇定时间分别缩短至0.76,0.82 s。
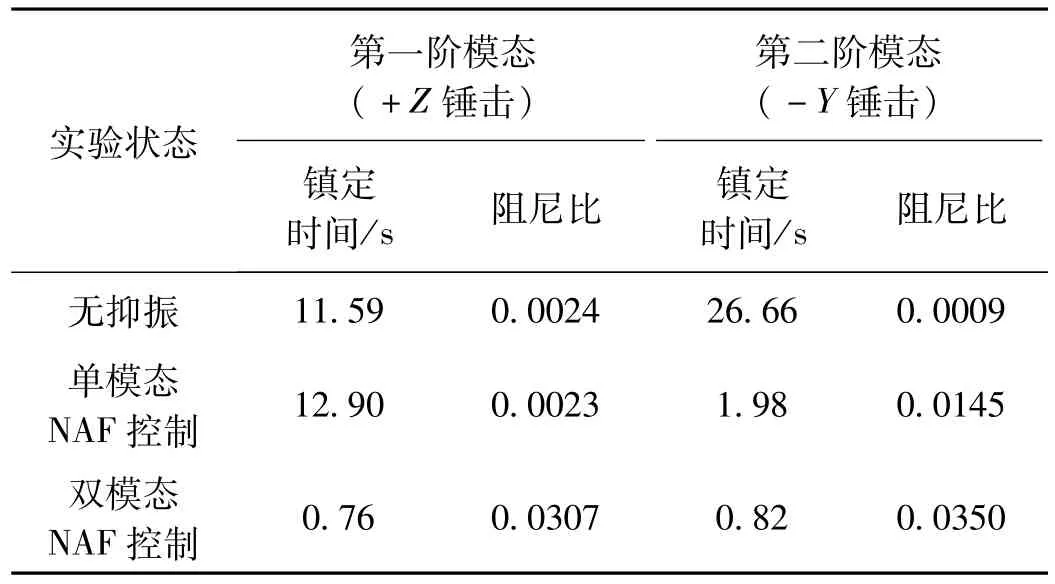
表2 锤击实验结果
5 结论
针对尾撑式风洞模型低阶模态强方向性振动问题,在异位配置NAF控制器基础上结合所设计的内嵌压电陶瓷作动器的风洞模型振动主动控制系统和模态分析结果,分别设计了针对第二阶模态和前二阶模态的单模态NAF控制算法和双模态NAF控制算法。锤击实验表明,双模态NAF控制下第二阶模态镇定时间相比单模态NAF控制缩短1.16 s,阻尼比提高2.4倍以上;双模态NAF控制缩短第一阶模态镇定时间近11 s,提高阻尼比近13倍。本文研究内容对风洞模型的振动控制技术的发展具有一定参考意义。
