变电站高耸避雷针顺风向风振响应分析
2020-06-17董新胜张军锋管品武
董新胜 张军锋 杨 洋 管品武
(1.国网新疆电力公司电力科学研究院,乌鲁木齐830011;2.郑州大学土木工程学院,郑州450001)
0 引 言
变电站作为电网的关键节点,其安全性至关重要。为避免雷击现象,变电站内往往建立高耸的独立避雷针,或者是在变电构架上安装避雷针,以保护设备的安全。避雷针结构属于典型的高耸结构,风振效应较为显著,并且偶有破坏事故发生[1-4]。但是,现行《变电站建筑结构设计技术规程》[5]仅简单对避雷针风振系数取值β=2.0,并未考虑结构形式、基频、阻尼以及场地类型和风速等影响风振效应的因素。
在众多形式的避雷针结构中,独柱避雷针的基频往往最小,故以一座典型独柱避雷针为例,在结构表面脉动风场模拟的基础上进行风振响应时程计算,分析了场地类型和风速的影响,并分析了位移、弯矩和剪力风振系数的差异。
1 工程背景和计算方法
本例位于新疆某750 kV变电站(图1),高度为60 m,其中顶部塔尖2 m,下部58 m塔身由7段变截面薄壁钢管组成,采用Q345钢材,每段钢管之间采用插接+法兰盘连接,钢管尺寸和插接长度见图1。采用ANSYS中的Beam188单元建模计算,计算中不含塔尖,不考虑钢管之间的插接重叠区,认为钢管之间仅为界面连接且为刚接。下部6段钢管均等分5个单元,最上部1段钢管为1个单元,共计31个单元。经动力特性计算可得其前5 阶侧弯振型如图 1(c)所示,频率f1~f5分别为0.751 Hz、2.09 Hz、4.31 Hz、7.46 Hz和 11.66 Hz。实际结构现场动力特性测试所得基频为0.713 3 Hz,与有限元结果吻合良好。由于下文风荷载沿X方向,图1(c)所列仅为XZ平面内的振型,因结构的对称性,YZ平面内亦有相同的振型。

图1 避雷针几何参数及有限元模型Fig.1 Geometry parameters and the FE model of the lightning rod
为评价场地类型的影响,根据荷载规范[6]和文献[7]选择4类场地(表1)计算。每种场地除考虑场地基本风速V0=35.8 m∕s外,还考虑V0=24 m∕s、30 m∕s、40 m∕s,共计四种风速,这也是荷载规范中V0的取值范围。其中B类场地V0=35.8 m∕s为基准工况。
由于避雷针等构筑物的设计控制指标为内力而非位移,故为得到内力的动力响应而采用时程计算。首先依表1参数和Davenport谱采用谐波叠加法[8-9]进行脉动风场模拟,再由准定常气动力假定得各节点脉动风荷载时程(式(1))。

表1 规范中场地参数取值[6-7]Table 1 Parameters for different terrain[6-7]

式中:Ai为节点迎风面积;空气密度ρ=1.25 kg∕m3;规范[5]阻力系数CD=0.6。
脉动风模拟采用单索引频率模拟方法[10-12],根据文献[8]所给参数取值原则取频率上限fu=6.0 Hz和时频点比值M∕N=2,即时间步长Δt=1∕12,以使后续动力计算中能充分计入结构的共振效应;模拟周期T0=600 s,共计7 200个时间点。图2给出了目标谱与模拟所得四个高度脉动风速样本风谱,可知模拟效果良好。

图2 目标谱与模拟所得四个高度脉动风速样本风谱Fig.2 Target and simulated wind spectrums for four locations
动力计算在ANSYS中进行,脉动荷载的每个时间步长Δt对应ANSYS求解中的一个荷载步。为准确计入动力效应,一般要求时程计算中的积分步长ITS<1∕(20fR),其中fR为需计入的最高阶模态对应的频率,对本例取f3=4.31 Hz,故取子步数为4。通过瑞利阻尼对前两阶频率取阻尼比ζ=1%和ζ=2%以分析阻尼的影响。另外,为校核时程结果,还采用频域法计入前5阶模态进行了计算,详见文献[13]。
2 结果分析
2.1 基准工况
采用阵风响应因子G表示风振效应。

图3给出了基准工况的风致静动力响应。可以看出,避雷针的动静力响应均符合悬臂结构受力特征;时域和频域所得根方差一致性良好,偏差在5%以内,也验证了时域结果的正确性。偏差的原因一方面是在频域计算中直接指定各阶模态的ζ=1%或ζ=2%,而时域方法瑞利阻尼所得高阶模态的不再恒有ζ=1%或ζ=2%;另一方面是时程计算结果直接与模拟所得样本风速有关,其结果不具有频域结果的统计特征。

图3 基准工况的风致响应Fig.3 The results of wind effects for the besic condtion
当ζ=1%时,从位移、弯矩和剪力阵风响应因子G的取值可分布可知,除基底局部高度范围剪力的G值小于2.0外,其他响应的G值均在2.0~3.0之间,明显大于现行《变电站建筑结构设计技术规程》[5]的风振系数取值2.0。这是由于此独柱避雷针的结构基频和阻尼较小,共振效应较为显著,明显大于背景效应(图4)。对比两种阻尼结果可知,当ζ由1%增加至2%时,共振效应显著下降,各响应的G值也都明显减小。这也说明规范的风振系数取值β应充分考虑结构风振效应的影响因素。
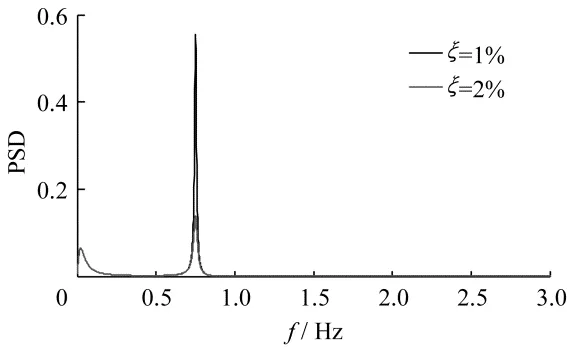
图4 顶点位移功率谱Fig.4 Spectrum of top displacement
另外,从图3(d)对比可知,对于整个结构高度,尽管位移和内力均值沿高度变化规律相反,但各响应均值和根方差沿高度的变化规律一致,故各响应G值均沿高度的增加而增加。但从数值对比可知,位移的G值明显小于内力的G值,并且内力G值沿高度的变化幅度也较位移G值更大。这说明传统按照位移所得阵风响应因子G值进行风振系数β取值对于避雷针结构是不合理的,这将低估脉动风荷载的风致内力,使结构设计偏于不安全。
对于避雷针结构,其荷载类型除自重外仅有风荷载,有条件对每个响应分别进行等效风荷载分析以获取各自的风振系数β:ζ=1%时,位移、弯矩和剪力的β分别取2.3、2.4和2.5;ζ=2%时,三者分别取2.0、2.1和2.2。图5给出以此所得等效静风响应与动力响应极值对比。由于弯矩和剪力的G值沿高度变化幅度较大,故尽管弯矩和剪力的等效静风响应在塔柱底部较动力响应极值偏大10%~15%,但在塔柱上端依然略小于动力响应极值,只是上部的内力幅值总体较小,实际并无碍于结构安全。位移的G值沿高度较为均匀,故其等效静风响应在塔柱底部较动力响应极值一致性良好,但其风振系数β却小于弯矩和剪力的β。
避雷针结构作为构筑物,设计过程中对内力尤其是弯矩更为关注,故实际设计中可仅根据弯矩响应确定风振系数β:对本例可取β=2.4(ζ=1%)或β=2.1(ζ=2%)。显然,β取值所得等效静风荷载所得位移始终大于实际动力位移,所得剪力在塔柱上部虽略有偏小,但因塔柱截面抗剪能力较高亦无碍设计安全。
2.2 多种影响因素分析
为考虑不同场地类型、风速的影响,依表1参数分别考虑A~D类场地配合V0=35.8 m∕s的计算以及B类场地四种风速的计算,分析共7种工况的阵风响应因子G并确定风振系数β(图6)。因钢结构设计往往偏保守取ζ=1%,故仅给出ζ=1%的结果,且仅给出弯矩的G值。可以看出,G值随着场地紊流度有显著增加,随风速亦有所增加但并不明显。
根据前文方法同样可确定7种工况的风振系数β:B类场地四种基本风速V0的β依次为2.1、2.3、2.4和2.4;而V0=35.8 m∕s对应的四种场地β依次为2.3、2.4、2.8和3.3。由此也可知,即使A类场地配合最小风速V0=24 m∕s,其风振系数β也不会小于2.0,现行《变电站建筑结构设计技术规程》取值β=2.0显然偏小,需在今后修订时考虑结构基频、阻尼、场地和风速的影响。
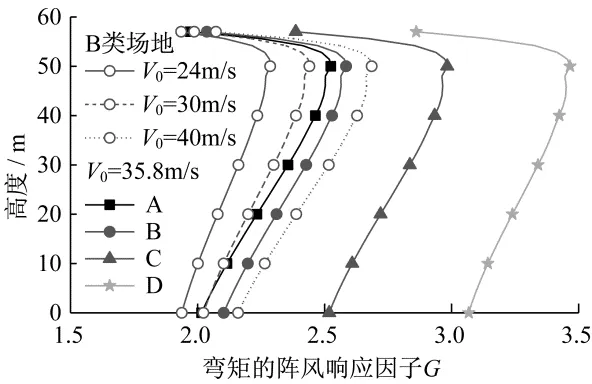
图6 不同工况的弯矩阵风响应因子Fig.6 Gust response factors for different conditions
3 结论
以一座典型独柱避雷针为例,在结构表面脉动风场模拟的基础上进行风振响应时程计算,分析了位移、弯矩和剪力风振效应的差异,并分析了结构阻尼、场地类型和风速对风振效应的影响,给出了不同参数对应的风振系数取值。具体结论如下:
(1)独柱避雷针结构基频较小,共振效应显著,并以一阶共振为绝对主力;各响应的阵风响应因子G有较大差异,位移的G值偏小且沿高度变化幅度不大,弯矩和剪力的值偏大且沿高度变化幅度较大。
(2)避雷针结构设计以内力尤其是弯矩控制,因此应以弯矩响应进行风振系数分析,由此得基准工况的β=2.4,明显大于现行《变电站建筑结构设计技术规程》取值β=2.0。
(3)结构阻尼和场地类型对风振效应的影响较大而风速的影响较小,且绝大部分工况的β取值均大于2.0,说明现行规程取值偏于不安全,在今后的修订中应对β取值考虑不同因素的影响。
