悬挑桁架的稳定性及关键节点承载力研究

何建平

（中铁第一勘察设计院集团有限公司，西安710043）

0 引 言

近年来，一些学者研究了悬挑桁架结构在设计及施工中的应用［1-5］。也有一些学者对空间大悬挑网壳结构整体稳定性进行了较为深入的理论分析，得到了一些能指导工程实践的研究成果［6-9］。学者对于大跨度网壳结构的稳定性研究的比较多，主要集中在稳定性和非线性极限承载力方面；对于悬挑桁架结构的研究相对较少，因此这种结构的稳定性方面还尚待深入研究。

以西安火车站（改扩建）东配楼项目为工程背景，对新建结构中悬挑外伸式层间桁架的稳定性设计及其关键节点承载力进行了研究。西安火车站（改扩建）东配楼项目为西安站站改工程的重要组成部分，总建筑高度为35.5 m，地上6层，地下2层（局部1层），建筑面积约93 000 m2，建筑功能为商业及办公。

本项目为了支撑上部屋盖结构的荷载，需要在建筑角部悬挑桁架，如图1所示。使用过程中悬挑桁架在竖向荷载作用下可能发生面外失稳，影响屋面结构的整体安全，需采取措施评价悬挑桁架的稳定性。长悬臂结构对竖向地震比较敏感，地震时变形过大可能会引起关键节点失效，需对悬挑层间桁架子结构进行分析，获得节点在复杂受力状态下的抗力水平，评价其安全性。

图1 东配楼效果图Fig.1 Renderings of east wing

1 悬挑层间桁架子结构稳定分析

为了支撑上部的屋盖结构，在结构的角部挑出一榀型钢混凝土桁架结构如图2所示，悬挑跨度为11.3 m，悬挑桁架楼层高度为4.4 m。此桁架实际上在结构中扮演挑梁角色，在上部荷载的作用下，可能存在面外失稳的风险。针对这一风险，悬挑层间桁架子结构稳定分析的技术路线为：首先通过线性稳定分析确定结构的最不利失稳模态；其次根据一致缺陷模态法将初始缺陷施加于结构当中；最后通过考虑几何、材料双非线性的稳定分析获取结构的极限承载能力，评价结构的稳定性能。

图2 东配楼悬挑桁架模型Fig.2 Cantilevered truss model of east wing

1.1 屈曲模态

特征值屈曲分析主要是分析悬挑桁架屈曲临界点的变形状态，是对其失稳模态定性分析判断的依据，同时往往还被作为初始缺陷模态的分布特征。由于局部桁架在整体模型中所占比例较小，不易捕捉到其失稳时的变形形式，所以采用ABAQUS有限元分析软件对边上位置的一榀平面桁架子结构模型进行单独分析，该悬挑结构中混凝土部分采用三维实体单元C3D8R；型钢采用4节点减缩积分单元S4R；钢筋采用三维二节点线性桁架单元T3D2进行分析。边界条件近似与原结构相同，所有杆件截面及布置形式均与提供的结构图一致。特征值屈曲分析的荷载工况选用1.0恒载+1.0活载组合，只选取其中典型且具有正特征值的屈曲模态，计算所得的1阶失稳模态如图3所示，特征值屈曲临界荷载系数如表1所示。

图3 单榀桁架1阶屈曲模态Fig.3 First order buckling mode of a single truss

表1 特征值屈曲临界荷载系数Table1 Critical load coefficient of eigenvalue buckling

经过分析可知：

（1）单榀桁架屈曲模态第1、4、5、8阶呈面外失稳，其余为钢腹杆局部屈曲，其中第1阶临界荷载因子高达154，达到曲屈荷载时，构件的材料可能已经发生破坏，在实际中几乎不可能发生，表明其在没有侧向约束的情况下不会发生失稳破坏。

（2）由于特征值屈曲分析假定材料为弹性材料，而且没有考虑大变形几何非线性和施工安装误差造成的初始几何缺陷的影响，其极限承载力为上限值，结构的实际极限承载力需要通过考虑双非线性的计算才能获得。

1.2 初始缺陷的引入方法

实际结构中不可避免的存在着各种初始缺陷。对于第二类极值点失稳，由于初始缺陷的影响可能使结构提前进入失稳状态，已有的许多文献表明，初始缺陷对一些结构的稳定承载力有很大的影响，甚至使稳定承载力下降达10倍以上。初始缺陷是稳定分析中必须要考虑的因素之一。

本文采用一致缺陷模态法来引入结构初始缺陷。一致缺陷模态法力图寻找出结构最不利的缺陷分布模式，认为由特征值屈曲分析得到的最低阶临界点对应的屈曲模态处于势能最小状态，因此，如果当结构的缺陷分布恰好与最低阶屈曲模态一致时，将对其产生最不利的影响。《空间网格结构技术规程》中建议采用一致缺陷模态法进行初始缺陷的施加，最大缺陷值可按网壳跨度的L／300取值；《钢结构设计规范》对压杆的初弯曲取值为L／1 000，《钢结构施工质量验收规范》对于梁弯曲矢高允许偏差为L／1 000，单层钢结构柱弯曲矢高允许偏差为H／1200；《混凝土结构工程施工质量验收规范》中对于构件变形偏离轴线位置的允许偏差为8 mm。本项目计算时参考《混凝土结构工程施工质量验收规范》，初始缺陷取值为8 m。

根据一致缺陷模态法，采取桁架失稳的第一阶模态作为初始缺陷的引入方式，在桁架节点荷载作用下，第一阶模态表现为平面桁架面外失稳，以此进行模型修正，将桁架下弦的未变形几何修改为具有8 mm的初弯曲状态。通过修改结构未变形时的节点坐标方法来实现。

1.3 非线性极限承载力

特征值屈曲分析主要是分析悬挑桁架屈曲临界点的变形状态，仅仅能对其失稳模态进行定性分析判断。采用二阶屈曲分析可以定量地得到考虑弹塑性几何非线性后结构的真实承载能力。根据前述线性分析可知，结构的屈曲临界荷载过大，根据常规设计，结构不可能承受如此大的荷载，在达到失稳临界荷载之前材料早已经发生了强度破坏而失效。线性分析得到的仅是没有考虑初始缺陷和材料的塑性性能，为了获得结构的实际承载力，验证该结构在强度破坏前不会发生失稳破坏，建立施加初始缺陷和考虑几何材料双非线性的单榀桁架子结构模型如图4所示。

图4 单榀平面桁架（单位：m）Fig.4 A single truss of plane trusses（Unit：m）

模型中的梁构件中型钢混凝土截面尺寸为600×1 400，内置型钢截面为 H1100×350×18×20；两个柱子型钢混凝土的截面尺寸为1 200×1 200，内置型钢截面为 H900×700×18×24；上下弦杆型钢混凝土的截面尺寸为600×1 200，内置型钢截面为H900×350×18×20。子结构模型的边界条件按照原结构模拟，柱下端为固定约束，梁7-9、8-10考虑现浇混凝土楼板的约束作用，因此限制7、8、9、10节点的面外位移和转动。按照结构的第一阶屈曲模态施加最大值为8 mm的初始缺陷，杆件的弹塑性性能通过分布于杆件上具有一定长度的纤维铰来模拟，将杆件截面划分成若干个纤维（图5），计算每个纤维的应力应变，通过积分得到杆件截面的内力与刚度从而得到截面的弹塑性性能，其相比于离散铰来说对于局部构件的分析更加准确。

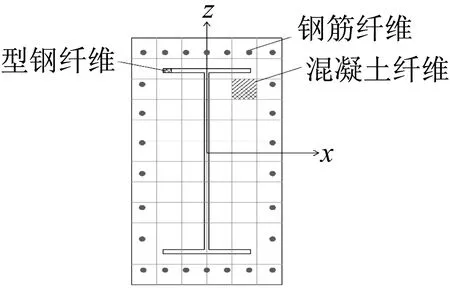
图5 纤维铰模型Fig.5 Fiber hinge model

在悬挑桁架节点1位置处施加单位荷载，采用逐步放大的方法进行逐步加载，根据位移收敛准则，达到目标位移后即停止加载，设置目标位移为2号节点竖向100 mm，分析时考虑几何非线性大变形效应，过程中捕捉节点2的竖向和面外荷载位移曲线如图6所示。

图6 节点竖向及面外位移Fig.6 Vertical and out-of-plane displacements of connections

由图6可以看出，桁架在加载的过程中，随着位移的增加荷载先是增加后保持不变，表明杆件截面发生了破坏，由弹性状态逐步转变成塑性状态，提取杆件2-4截面纤维的应力应变曲线可以发现外侧混凝土纤维已经达到极限压应变，表明此时已经达到桁架的极限承载能力，承载力为3 750 kN，约为设计荷载D+L的9.8倍。图6可以看出，由于杆件初始缺陷的存在，在竖向荷载的作用下，桁架会发生扭转而产生面外的位移。随着荷载的增加面外位移也逐步增加，但在达到极限荷载之前并没有出现曲线斜率为0或为负值，也就是荷载不再增加或荷载减小而位移增大的现象，表明材料在破坏前不会发生面外失稳的情况，验证了悬挑桁架的稳定性，证明了其承载能力并不是由稳定性控制而是由强度控制。根据前述线性稳定的分析结果，失稳时临界荷载为设计荷载D+L的上百倍，而考虑弹塑性几何非线性后结构的真实承载能力为9.8倍，说明了对于型钢混凝土桁架这类刚度较大的结构不同于钢桁架、钢网架等柔性结构，强度是主控因素。

2 关键节点承载力分析

2.1 关键节点参数

型钢混凝土柱与悬臂桁架连接节点是具有高安全性的关键节点，节点处受力较大，桁架节点承受梁端、柱端、斜杆传来的轴力、弯矩和剪力，处于复合受力状态，内力传递机理较复杂且受很多因素如节点连接的框架梁类型、型钢混凝土柱中所配制的型钢样式和节点连接的构造形式等影响。因此对项目中该类节点进行精细化有限元分析，基于足尺度三维模型，采用Abaqus有限元分析软件，节点计算选自与悬臂桁架相连部分关键位置。各关键节点的位置分布如图2所示。关键节点局部图如图7所示。其中：1#节点选自2-7轴悬臂桁架下弦根部节点；2#节点选自2-8轴悬臂桁架上弦根部节点；3#节点选自2-8轴悬臂桁架上弦与腹杆及支撑交汇处节点。

图7 关键节点几何模型Fig.7 Key connection geometry model

1）节点几何参数

各个节点的构造、尺寸及其材料如表2-表4所示。

表2 1#节点材料表Table 2 1#Connection material list

2）单元类型

混凝土单元选用8节点六面体缩减积分的三维实体单元C3D8R。这种单元的自由度较少，可以在很大程度上减少计算时间，并且可以避免使用完全积分产生的刚度过大，而计算结果足以反映混凝土的实际应力应变。另外，当网格存在扭曲变形时，分析精度不会受到太大的影响，不会出现剪力自锁现象；模型的适应性较强。型钢采用4节点减缩积分单元S4R，该单元具有很好的适用性，既可以用于厚壳问题的模拟，也可以用于薄壳问题。钢筋模拟采用三维二节点线性桁架单元T3D2，该单元具有水平位移和垂直位移两个自由度。计算结果有足够的精度要求，且计算代价小。

表3 2#节点材料表Table 3 2#Connection material properties

表4 3#节点材料表Table 4 3#Connection material properties

3）材料本构

采用ABAQUS提供的混凝土损伤塑性模型（CDP模型）。CDP模型假定混凝土材料主要因拉伸开裂和压缩破碎而破坏。屈服或破坏面的演化由两个变量ε͂plt（拉伸等效塑性应变）和ε͂plc（压缩等效塑性应变）控制。在弹性阶段，该模型采用线弹性模型对材料的力学性能进行描述，进入损伤阶段后，CDP模型损伤后的弹性模量可以表示为损伤因子d和初始无损弹性模量的关系式：

式中：E0为初始（无损）弹性模量；损伤因子d为应力状态和单轴拉压损伤变量dt和dc的函数，在单轴循环荷载状态下，ABAQUS假定：

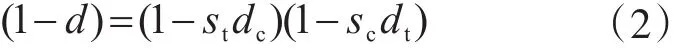
式中，分别为与应力反向有关的刚度恢复应力状态的函数，用以下两个方程定义：

其中：

权重因子wt和wc为材料参数，控制着反向加载下材料刚度的恢复。σ11字符无定义。

钢筋和型钢的本构模型釆用Abaqus中的塑性分析模型。该模型在多轴应力状态下满足Mises屈服准则，釆用各向同性的强化准则，服从相关流动法则。钢筋与型钢的本构关系分别釆用二折线强化模型。其应力-应变关系如下式所示：

式中，εs=fy/Es为屈服应力，E′s=0.01Es。

4）模型网格划分、边界及加载条件

目前对于复杂节点的受力分析研究主要基于节点模型隔离的方法。钢-混凝土组合节点分析模型中构件长度一般取为2～3倍构件截面高度。本模型在网格划分前先将实体模型划分为多个几何形状规则的区域，由于划分区域几何形状较为规则，故本模型均按结构网格划分技术对模型进行网格划分，关键节点网格划分如图8所示。

图8 关键节点网格划分Fig.8 Key connection meshing

根据SAP2000的整体结构分析计算结果，选取多遇和罕遇地震下节点若干不利荷载组合工况中的一种（1.2恒载+0.6活载+1.3竖向地震），提取响应的杆件内力，在距离端部面10 cm处设置参考点以施加荷载，尽量减少对边界处的应力集中现象。模型采用简化的边界约束方式，即选取柱的杆件端面（一般为柱底）施加位移边界条件，同时由此产生的节点内应力分布状况和变形与实际情况尽可能一致。释放其余杆件端部约束，仅施加荷载边界条件。默认构件中布置了足够的抗剪栓钉以不考虑型钢和钢筋与混凝土的相对滑移，通过约束嵌入到混凝土中。多遇地震作用下关键节点承载力有限元模型的边界及荷载加载情况如图9-图11所示。

图9 1#节点边界及荷载加载模型Fig.9 Boundary and load loading model of connection 1#

图10 2#节点边界及荷载加载模型Fig.10 Boundary and load loading model of connection 2#

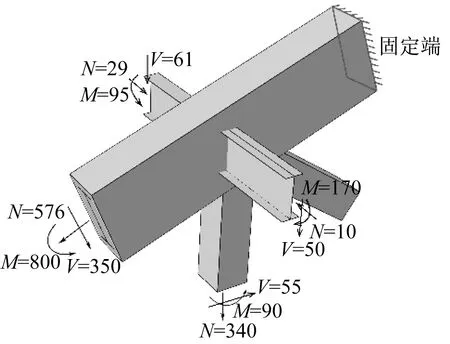
图11 3#节点边界及荷载加载模型Fig.11 Boundary and load loading model of connection 3#

2.2 有限元分析结果

多遇地震作用下1#节点混凝土第一主应力及型钢Von Mises应力如图12左侧所示。罕遇地震作用下1#节点混凝土第一主应力及型钢Von Mises应力如图12右侧所示。

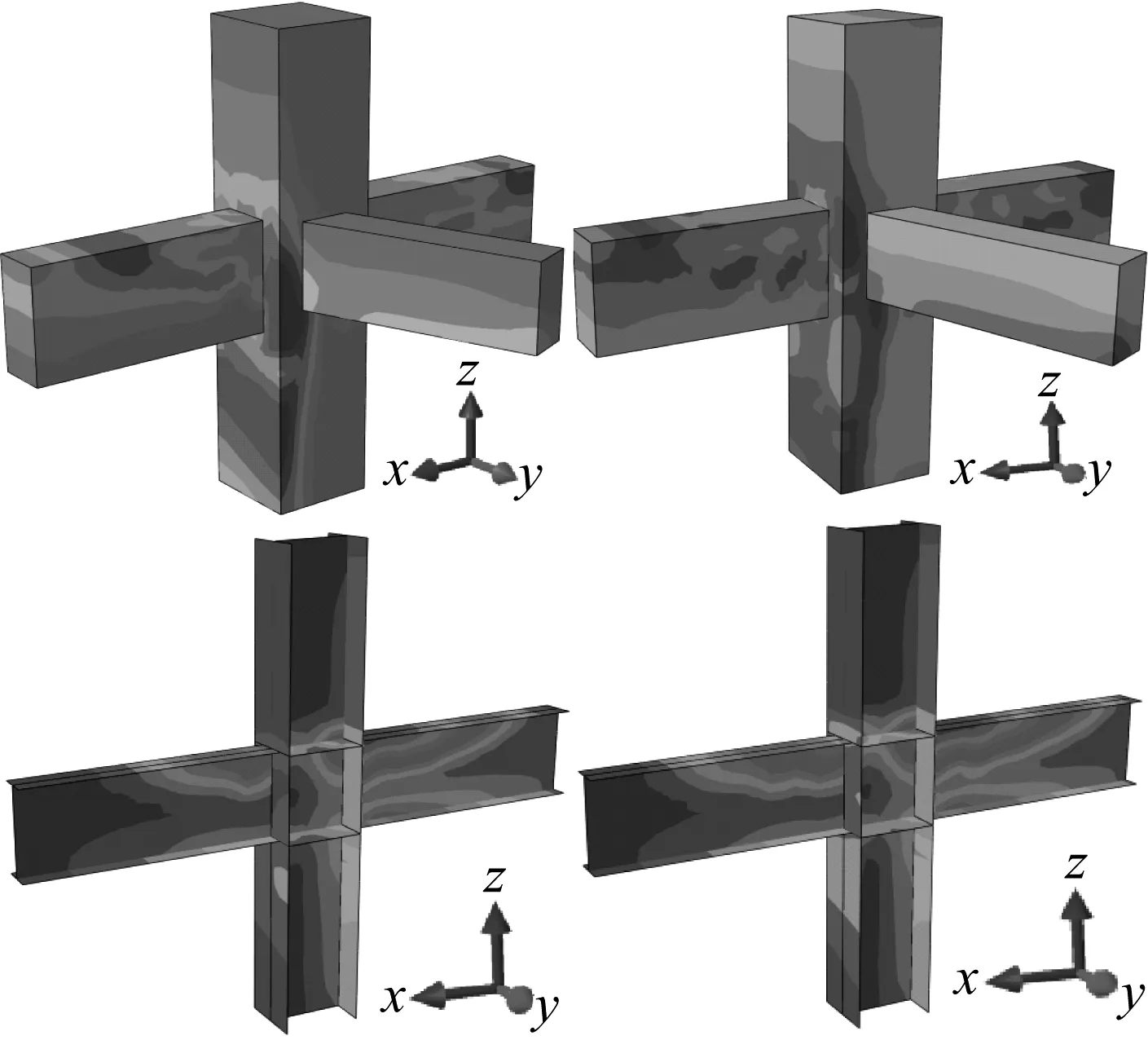
图12 1#节点应力图Fig.12 Stress contour for connection 1#

1#节点在设计荷载多遇地震（1.2D+0.6L+1.3EZ）下，节点悬挑部位受力最大，将内力传递至柱子和相连的框架梁。内部型钢上翼缘受拉区应力最大。受拉钢筋最大轴向拉应力为216 MPa。型钢、钢筋均处于弹性阶段，混凝土柱在悬挑构件作用下一侧产生了较大的拉应力，梁端离加载部位较近处有应力集中现象，局部应力达到抗拉强度，绝大部分拉压应力均较小。罕遇地震作用下，节点传力形式不变，内部型钢最大Von Mises应力约为190 MPa。受拉钢筋最大轴向应力289 MPa。受压应力在梁柱连接角部部位有应力集中，压应力超过抗压强度被压碎。总结：1#节点在多遇和罕遇地震下，内部主要受力构件型钢、钢筋均处于弹性阶段，混凝土作为连接和安全储备，伸臂桁架内力能通过节点可靠传递。

多遇地震作用下2#节点混凝土第一主应力及型钢Von Mises应力如图13左侧所示。罕遇地震作用下2#节点混凝土第一主应力及型钢Von Mises应力如图13右侧所示。

图13 2#节点应力图Fig.13 Stress contour for connection 2#

2#节点在设计荷载多遇地震（1.2D+0.6L+1.3EZ）作用下，节点内力主要由型钢混凝土梁传递，钢筋混凝土梁内力较小。节点部型钢上翼缘根部应力最大。周围梁内受拉钢筋轴向应力均处于弹性阶段，节点内混凝土柱传递周围梁的弯矩产生较大的拉应力，裂缝主要分布在梁上部受拉区和柱顶，压应力在梁根处有应力集中现象，其余部位均处于弹性阶段。罕遇地震作用下型钢混凝土构件上翼缘最大Von Mises应力为275 MPa，钢筋应力为330 MPa，与柱斜交钢筋混凝土梁中2根受拉钢筋达到屈服强度，悬挑梁根部混凝土受压破坏。总结：2#节点在多遇和罕遇地震下，内部型钢能可靠的传递各杆件内力，但钢筋混凝土梁截面相对来说比较薄弱，有一定破坏但没有失效。

多遇地震作用下3#节点混凝土第一主应力及型钢Von Mises应力如图14左侧所示。罕遇地震作用下3#节点混凝土第一主应力及型钢Von Mises应力如图14右侧所示。

图14 3#节点应力图Fig.14 Stress contour for connection 3#

3#节点在设计荷载多遇地震（1.2D+0.6L+1.3EZ）作用下，节点主要受弦杆和腹杆的轴力和弯矩作用。型钢、钢筋受力较小均处于弹性阶段，混凝土主拉应力在两端有偏大现象，为加强的边界条件所致，在腹杆处压应力最大，为8 MPa。罕遇地震下，型钢最大Von Mises等效应力为143 MPa，钢筋为150 MPa，混凝土拉应力在杆端处偏大，压应力在腹杆处为17 MPa，其余均较小。总结：3#节点在多遇和罕遇地震作用时受力较小均能保持弹性的工作状态。

3 结论

（1）悬挑层间桁架子结构稳定分析的技术路线是可行的。结果表明结构在材料破坏前不会发生面外失稳，结构的极限承载能力不是由稳定性控制而是由材料强度控制。

（2）基于空间实体单元的微观尺度有限元模型可以较好地反应其材料损伤、开裂、屈服失稳等局部非线性行为，可以得到结构的关键部位抗力水平，从而能更好地理解、把握结构的性能。分析结果表明，在设计荷载小震作用下，节点区混凝土受拉区产生裂缝，型钢和钢筋均处于弹性状态，无明显的应力集中现象，最大应力均小于材料屈服应力，满足小震弹性的设计要求。在大震作用下，各节点混凝土受拉区裂缝开展更深，分布更广，部分受拉钢筋屈服，内部型钢处于弹性阶段，由于设计主要考虑型钢的作用，混凝土仅作为连接需要和安全储备，满足大震不坏的设计要求。