混凝土排水管道内部腐蚀研究

高向玲 王丽娜 刘 威

（同济大学土木工程学院，上海200092）

0 引 言

随着经济的进步，城市规模逐渐扩大，城市排水管网建设不断发展。截止2017年底，我国城市排水管道总长已达63.0万km，建成区排水管道密度为8.56 km∕km2。混凝土排水管道由于其良好的承载力和耐腐蚀性能，在排水管道中广泛采用［1］。德国混凝土排水管道占比42%［2］；波兰一些城市，混凝土排水管的占比大于50%［3］；调查数据显示，2018年上海市某区的混凝土排水管道占地区管道总长的68%。随着我国污水治理工程的加大、加快，我国钢筋混凝土排水管应用的最大规格直径达到4 000 mm［4］。

20世纪40年代接连发生运行中的混凝土管道遭受污水侵蚀而破坏的案例，使得人们开始重视混凝土管道受污水腐蚀的研究。近年来，加拿大［5］、美国［6］、澳大利亚［7］等国家的研究人员均指出当前混凝土排水管道的腐蚀急需修复，且修复费用昂贵。腐蚀是影响混凝土排水管道寿命和可靠性的主要因素之一［8］。

排水管道一般都埋置于地下，腐蚀程度主要受环境因素和材料因素的影响，其所受腐蚀包括外部腐蚀（土壤和地下水腐蚀）和内部腐蚀（污水腐蚀）。建设在西安、济南、沈阳等地的土壤腐蚀试验站的统计结果显示，经过30年的埋设钢筋混凝土试件的最大中性化深度为10.3 mm［9］；奥地利东部地区某一混凝土排水管道，内部腐蚀速率大于10 mm∕y，使用寿命小于10年［10］。可见，管道内部腐蚀程度大于外部腐蚀，所以本文主要讨论混凝土排水管道的内部腐蚀。

1 混凝土管道内部腐蚀机理

按侵蚀介质种类可将污水对混凝土的腐蚀分为无机物腐蚀和微生物诱导腐蚀。微生物诱导腐蚀是在适当的环境下，微生物分解消化有机物，释放有机酸、二氧化碳和硫化氢等腐蚀性介质，腐蚀性介质与混凝土发生化学反应侵蚀混凝土［11］。混凝土管道内的腐蚀最主要的是微生物诱导腐蚀。因此，接下来将以微生物诱导腐蚀为主展开研究。

1.1 微生物诱导腐蚀发生位置

实际管道内部腐蚀损失严重的区域位于管道内污水液面以上，主要是微生物诱导产生的腐蚀。图1（a）中腐蚀最严重部位的腐蚀深度达到管道壁厚的 82.3%［3］。

1.2 微生物诱导腐蚀发生机理

Parker在1945年指出由微生物诱导的生物化学反应是导致混凝土腐蚀的主要原因之一，并将其称为生物硫酸腐蚀［12］。微生物诱导腐蚀过程包括物理、化学、生物-化学作用［11］。

图 1 管道腐蚀情况［3，7］Fig.1 Corrosion condition of pipeline

图2 污水腐蚀的反应过程［15］Fig.2 Reaction process of sewage corrosion

Jiang等［16］通过试验测定腐蚀产物中钙与硫的摩尔比约为1.4，表明腐蚀产物中同时存在石膏与钙矾石。荣辉等［17］通过对污水环境下微生物对混凝土的腐蚀试验研究得出，当硫酸根离子浓度小于1 000 mg∕L时，腐蚀产物主要是钙矾石；当硫酸根离子浓度大于8 000 mg∕L时，主要产物为石膏；当硫酸根离子浓度在两者之间时，腐蚀产物为钙矾石和石膏。钙矾石和石膏将进一步诱发混凝土的膨胀，从而导致胀裂。

2 微生物诱导腐蚀模型

发展能够预测排水管道腐蚀程度的模型，对于掌握排水管道的使用寿命至关重要。从模型特征来看，预测微生物诱导腐蚀的模型可以分为粗略预测模型、腐蚀速率模型和腐蚀深度模型三类。

2.1 粗略预测模型

1970年Pomeroy［18］提出了Z指数计算公式，根据Z值可粗略评价硫化物对管道的腐蚀影响。当Z≤5 000时，水中没有硫化物产生；当Z在5 000～10 000之间时硫化物产生的概率较小，Z＞10 000时，硫化物产生的概率较大。但是Z指数对管道腐蚀的评价只是定性的，且只适用于重力式排水管道。

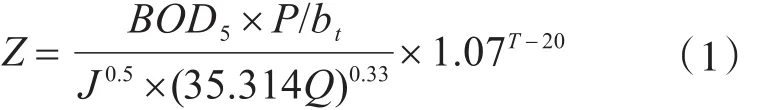
式中：J为管线坡度（m/m）；Q为管道流量（m3∕s），Q=SV，其中，S为水流有效断面面积（m2）；V为水流速度（m∕s）；P为湿周（m）；bt为水面宽度（m）；BOD5为5天生物需氧量（gO2∕m3）。

Saegrow［19］通过采用BOD与COD的比值更详细地描述有机物的降解，并考虑到污水pH值对腐蚀的影响，对Pomeroy提出的Z指数计算公式进行了改进。

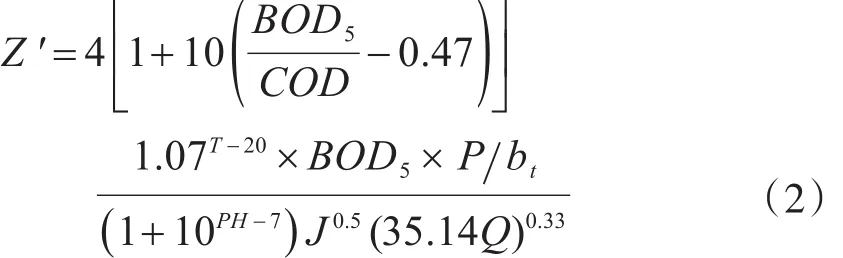
式中：PH为污水的pH值，≥7.5；COD为化学需氧量（gO2∕m3），0.4≤BOD5COD≤ 0.6。

2.2 腐蚀速率模型

USEPA［20］根据管壁吸收的硫化氢含量、混凝土材料碱度、酸反应系数等建立平均腐蚀速率模型。该模型所考虑的因素较为全面。

式中：c为平均腐蚀速率（mm∕y）；k为硫酸与水泥材料反应程度的相关性系数，酸形成较慢时为1.0，酸形成较快时为0.3；A为管道材料碱度，在花岗岩骨料制成的混凝土管道中，碱度通常在16%～24%，石棉水泥管道的碱度通常在50%左右；Φsw为传递到管壁的硫化氢值（g∕（m2·hr））；s为管线坡度（m∕m）；u为管流速度（m∕s）；j为与pH相关的硫化氢系数（表1）；b/p'为水流表面宽度与外露周长之比。

表1 系数j的参考取值Table 1 The values of factor j

ASCE［21］通过引入管顶腐蚀系数和湍流腐蚀系数反映管道截面腐蚀的不均匀性，给出了管道内最大腐蚀速率Cmax（mm∕y）计算公式。

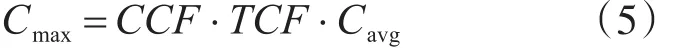
式中，CCF为管顶腐蚀系数，一般取1.5～2.0；TCF为湍流腐蚀系数，设计良好的跌水取1～2.5，急剧下降或其他湍流交汇处取5～10；Cavg为平均腐蚀速率，可参考USEPA［20］，其中，混凝土碱度对于花岗岩（硅质）骨料混凝土为0.17～0.24，对于石灰岩（钙质）骨料混凝土为0.9～1.1，对于混凝土砂浆衬管以及石棉水泥管均为0.5。

Wells和 Melchers［22］根据澳大利亚的珀斯、悉尼、墨尔本三个城市重力下水道中所进行的原位腐蚀试验的检测结果，建立了与污水温度、H2S浓度和相对湿度有关的混凝土管道受微生物腐蚀速率模型。模型计算比较简单，但其中变量需要在具体管道测得。

式中：C为平均腐蚀速率（mm∕y）；A为比例系数（mm·ppm-0.5∕y），可由数据拟合得出；［H2S］为管道中硫化氢浓度（ppm）；H为管壁相对湿度；R为通用气体常数，可取8.314J∕（mol·K）；T为管道内温度（K）。

2.3 腐蚀深度模型

fib［23］结合pH值与硫酸浓度的关系，建立了与时间相关的腐蚀深度预测模型，可以将腐蚀实时化。但仅仅通过pH值的变化考虑环境因素对管道腐蚀的影响，略显简单。

式中，d为腐蚀深度（m）；kc为混凝土材料系数，更多细节请参考文献［24］和［25］；c为酸浓度（mol∕L），c=10-PH，其中PH为酸的pH值；t为侵蚀时间（s）。

此外，Belie等［26］通过试验研究发现水灰比对混凝土管道腐蚀深度有影响，提出了考虑混凝土碱度和吸水率的腐蚀深度计算模型。由于模型只是在实验室内的加速试验中得以验证，而加速腐蚀试验与实际腐蚀情况之间等价关系尚不明确。因此，该模型在预测实际混凝土管道的腐蚀程度方面的应用有待进一步的发展。

3 模型比选分析

Wu等［27］对加拿大埃德蒙顿市混凝土排水管道微生物腐蚀的研究，得出影响微生物腐蚀速率的三类主要因素：水力参数（污水流速、扰动、停滞时间）、环境因素（相对湿度、溶解氧含量、生物需氧量、污水温度、环境温度、污水pH）、混凝土材料参数（孔隙度）。然而，现有混凝土受微生物腐蚀速率模型中所采用的因素变量差异较大。因此，本文将基于现有的文献数据，结合模型的特征，对USEPA［20］、ASCE［21］、Wells［22］、fib［23］模型进行比较与分析。

3.1 文献数据分析

通过总结文献［7，10，12，22，28-32］中的数据，得到了混凝土管道腐蚀深度值与时间的关系，见图3。图中，［7］中的S表示标准混凝土管，C表示钙质骨料混凝土管，R表示抗硫酸盐水泥混凝土管，H表示高压成型混凝土管；［22］和［28］中的N表示新混凝土，O表示旧混凝土，P表示珀斯，M表示墨尔本，S表示悉尼，A、B表示地区；［31］中PC表示波特兰水泥，SIL表示硅质骨料，DOL表示白云岩骨料，CAC表示铝酸钙水泥。

3.2 模型参数取值

通过各模型与实测数据的对比，选择具有普适性的模型。计算模型中所涉及的参数在试验中已给出的则选用试验中的值，试验中没有记录的参数则依据文献［20、22-25、32-36］按照以下原则取用。

图3 腐蚀深度与时间的关系Fig.3 Relation between corrosion depth and time

腐蚀深度d（mm），时间t（y），腐蚀速率c（mm∕y）；腐蚀系数k为0.85，混凝土碱度A为0.2，污水温度T为25℃，污水pH值为7.5，管道坡度J为0.000 5 m∕m，污水充满度μ为0.5，溶解于水的硫化物总量DS为0.702 mg∕L，管道中H2S浓度为80ppm，管顶腐蚀系数kccf为1.5，扰动系数ktcf为1，管壁相对湿度H为95%，材料系数kc为8.12×10-4m·（s·mol∕l）-0.5，管流速度 V 为 1.42 m∕s，通用气体常数R为8.314 J∕（mol·K），比例系数a为1.81×108mm×ppm-0.5∕y，管道直径D为3 m；计算可以得出液面宽度bt为3 m，液面以上管道周长U为4.71 m，湿周P为4.71 m。模型管道中采用混凝土排水管中使用最多的硅酸盐水泥（Portland Cement）。混凝土的水灰比为0.45，砂灰比为1.44。

3.3 模型对比分析

根据 USEPA［20］、ASCE［21］、Wells［22］腐蚀速率模型和fib［23］的腐蚀深度模型以及3.2节给出的模型参数预测3.1节中管道的腐蚀深度，并将各模型的预测结果与实测结果进行比较。模型预测值与试验实测值的比值及其比值的均值与方差分别见图4和图5。

根据式（8）计算各模型预测值的相对误差，将超过600%的相对误差取为600%，结果见图6。

根据图4-图6中四个模型预测的腐蚀深度与实测结果的对比可以得到如下结论：

（1）USEPA［20］∕试验的离散性最小，但是其均值小于1，即若以此模型预测将低估腐蚀程度，偏于不安全；在其余模型中，fib［23］预测值与试验值之比的均值最接近1，且其标准差最小。因此，fib［23］模型最适用于预测混凝土排水管道的腐蚀深度。

图4 模型计算结果与试验值的比值Fig.4 The ratio of calculated results to test results

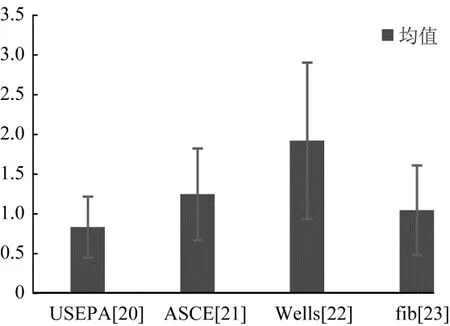
图5 模型∕试验的均值±标准差Fig.5 Mean±standard deviation of the ratio between calculated results and test results

（2）USEPA［20］比较适用于硅酸盐水泥，对于铝酸钙水泥混凝土的腐蚀深度预测误差较大；USEPA［20］总体的预测结果偏小，应对管顶腐蚀系数予以考虑。

（3）ASCE［21］在 USEPA［20］的基础上考虑了管顶系数的影响，可在一定程度上提高一些管道的预测精度，但在一些管道中仍然存在预测偏低的情况，可能是未考虑湍流对腐蚀的影响。对预测偏低的数据计算试验值与ASCE［21］的比值，可以得出湍流系数范围1.04～9.7，其值落在ASCE［21］所给出的湍流影响系数范围（1～10）内，由此得出可以根据ASCE［21］预测管道内的最大腐蚀深度。

（4）fib［23］可在一定程度上有效地预测管道的平均腐蚀深度，但其预测的腐蚀深度有时偏低，结合 ASCE［21］，建议在 fib［23］模型中适当考虑管顶系数和湍流系数，以预测最大腐蚀深度。

（5）在相同环境中，测试时间越长，Wells［22］模型越适用；根据现有数据拟合得出模型中的比例系数，然后结合管道环境特征，采用 Wells［22］可以有效预测出管道的腐蚀深度。

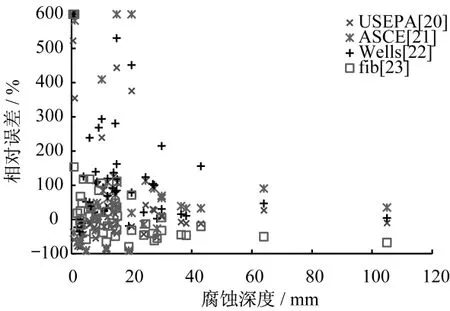
图6 腐蚀深度相对误差Fig.6 Relative error of corrosion depth

（6）腐蚀模型对旧混凝土腐蚀深度的预测普遍较小，可能是腐蚀产物的产生，破坏了混凝土内部原有结构，增加了混凝土的孔隙度，因而加速了腐蚀。

以上模型是基于原位试验或实际管道的腐蚀并与微生物腐蚀机理相结合得出的半经验半理论或经验公式。由于影响管道腐蚀的因素复杂多变，试验投入的时间成本较高，一些学者则通过数值模拟的方法研究混凝土受污水中微生物侵蚀的机理、过程以及混凝土的腐蚀速率。

4 管道腐蚀的数值模拟

4.1 腐蚀模拟原理

对于管道腐蚀的模拟，从分析方法来看，可分为基于腐蚀模型的模拟、依据现象学理论的模拟、根据化学反应基于Fick定律的模拟。同时，通过引入不确定性可考虑腐蚀的随机性。

混凝土排水管道的微生物诱导腐蚀过程主要包括硫化物的生成、H2S的运输、H2SO4的生成以及H2SO4对混凝土的侵蚀四个阶段。对于管道腐蚀单物理场的模拟多集中在后三个阶段。

发生在排水管道中的微生物腐蚀主要是硫酸对混凝土的腐蚀，其中既有H+的溶蚀作用，也有SO42-的膨胀作用［37］。忽略侵蚀离子与混凝土材料发生的化学反应，侵蚀离子在混凝土中的扩散过程可以用Fick第二定律描述［38］。式中：C为侵蚀介质浓度（mol∕m3）；D为侵蚀介质的扩散系数（m2∕s）。

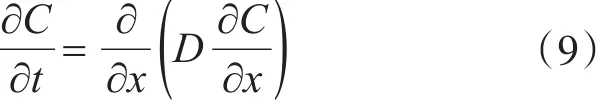
从式（9）可以看出，扩散系数是影响侵蚀介质在混凝土中浓度分布的主要因素。同时介质在混凝土中的扩散系数受混凝土材料孔隙度、水灰比、掺合料、龄期等诸多因素的影响。

4.2 硫酸根离子的扩散系数

硫酸根离子的扩散系数（m2∕s）主要有以下几种：

（1）适用于水灰比（w∕c）不小于0.3的硫酸根离子扩散系数［39］：

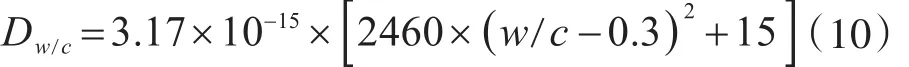
（2）与时间相关的硫酸根离子扩散系数［40］：

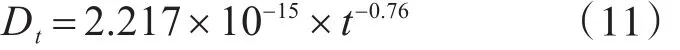
式中，t为接触时间（月）。

（3）考虑混凝土材料的孔隙度与侵蚀损伤对扩散系数的影响［41］：

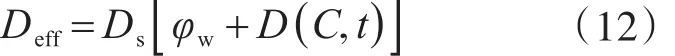
式中，Ds为在混凝土孔隙溶液中的初始扩散系数（m2∕s）；φw为混凝土材料的孔隙度；D（C，t）为混凝土材料的损伤函数；其具体计算与取值详见文献［37，42-43］。

4.3 氢离子的扩散系数

Jahani等［44］的研究指出，在 H+稳定扩散阶段（扩散初期）扩散系数为DH=8.91×10-13m2∕s。

4.4 数值模拟

根据上述分析，分别采用Dw/c、Dt、Deff和DH4种扩散系数对文献［30］和［28］中的新混凝土腐蚀深度进行预测。文献中的腐蚀深度与介质浓度及腐蚀时间的关系见表2。

表2 试验中的腐蚀条件和结果Table 2 Corrosion conditions and results in tests

对于Dw/c中的水灰比取0.45；在确定Deff时，首先需要确定Ds。

假定扩散系数为常数，且混凝土内侵蚀介质的初始浓度为0时，式（9）的解为

式中，Cx为x位置处侵蚀介质的浓度（mol∕m3）；C0为侵蚀介质初始浓度（mol∕m3）；t为侵蚀时间（s）；erfc（x）为互补误差函数。

将3.1文献数据中的腐蚀深度、腐蚀时间和侵蚀介质浓度带入式（13），界定临界腐蚀浓度Cx=Clim=1.0×10-7mol∕l［23］，计算各试验的常扩散系数，将其均值取为侵蚀介质在混凝土孔隙溶液中的初始扩散系数，得到Ds=4.18×10-13m2∕s。

应用COMSOL MULTIPHYSICS软件，采用Dw/c、Dt、Deff和DH4 种侵蚀介质的扩散系数进行混凝土腐蚀深度的数值模拟，所得的腐蚀深度与试验值的对比见图7。

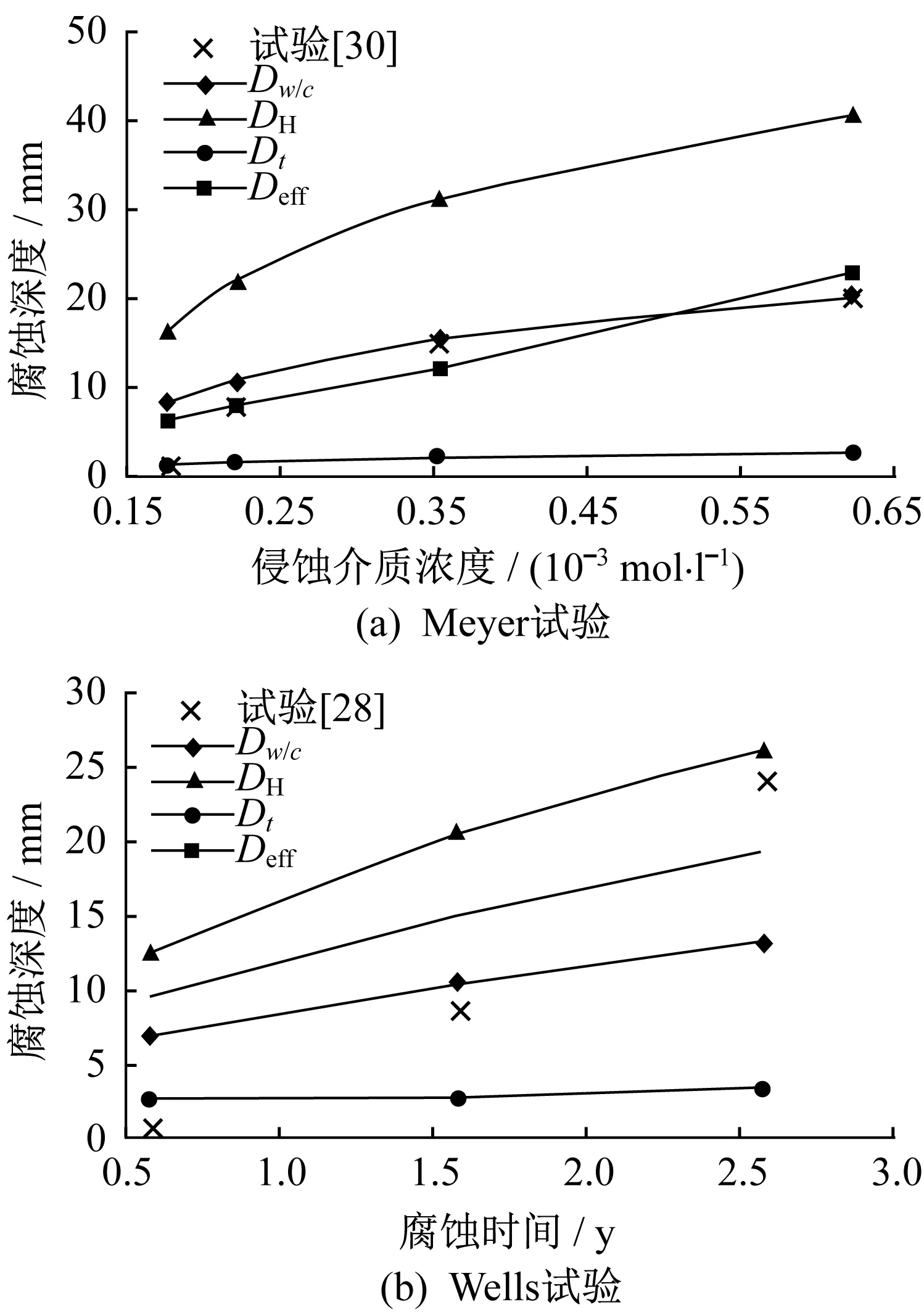
图7 模拟结果与试验结果的比较Fig.7 Comparison of simulation results with experimental results

图 7（a）中，对比 Dw/c、Dt的模拟结果和试验结果可看出，扩散系数随侵蚀介质浓度的增加而增加；从Dw/c模拟结果与试验结果的对比可看出，当侵蚀介质浓度达到一定值时，扩散系数趋于定值，其量纲为 10-13m2∕s。

图7（b）中，腐蚀时间为1.58年时Dw/c的模拟结果与试验值最接近，而腐蚀时间为2.58年时DH的模拟结果与试验值最接近，DH＞Dw/c，由此可以得出，侵蚀介质的扩散系数与时间呈正相关关系。

硫酸根离子的扩散系数Deff与腐蚀时间和侵蚀介质浓度的关系与图7（a）和图7（b）所得规律相符。因此，可以采用Deff形式的扩散系数，并结合式（9）的扩散规律模拟混凝土的腐蚀。

5 结 论

通过对不同腐蚀模型的对比分析以及对管道腐蚀模拟的研究，本文主要得出以下几个结论：

（1）对于污水混凝土管道腐蚀深度的预测，采用腐蚀深度模型优于平均腐蚀速率模型；

（2）对管道腐蚀的预测需要考虑管道截面内位置（多为管顶）和管道内部扰动的影响，应用fib［23］模型预测管道的腐蚀深度较为合理；

（3）采用扩散系数模型Deff，并结合Fick第二定律可以得出侵蚀介质在混凝土中的浓度分布，通过界定侵蚀介质的临界浓度可以得出混凝土的腐蚀深度。