利用随钻电磁波测井探测直井水力裂缝的正演模拟

谢 媛， 刘得军， 李彩芳， 翟 颖， 孙 雨

（中国石油大学（北京）信息科学与工程学院，北京 102249）

近年来，随着油气资源勘探水平的不断提高和油气需求的不断增加，低渗透油气藏的开发引起了国内外石油领域专家和相关企业的高度关注。该类油气藏需要利用水力压裂方法提高储层的渗流能力，才能高效开发[1]。提高压裂效率和效果，需要了解水力压裂产生裂缝的分布情况。

近年来，国内外监测水力裂缝的技术方法发展较快。D. Xue 和 G. D. Hu 等人[2-3]采用常规感应测井（＞10 kHz）方法推测钻孔周围裂缝的长度、电阻率和倾角；D. Pardo 和 C. Torres-Verdin[4]采用数值模拟方法评估了采用低频（＜1 kHz）电磁感应方法监测垂直裂缝长度的可行性；Yang Kai等人[5]针对水力压裂裸眼井的情况，定量分析了发射-接收间距、工作频率以及裂缝形状、横截面积、倾角和导电率对比度对测井响应信号的影响。目前，定性分析、评价与检测水力裂缝的方法虽有报道，但从理论上看，对裂缝监测进行系统化、综合性的研究还很少。传统的井温测井、同位素测井、注硼中子寿命测井等方法在监测水力裂缝方面存在施工时间受限、准确性差等缺陷，且同位素测井、注硼中子寿命测井等核测井方法还会对地层造成一定污染，不适合推广应用[6-7]。声波测井监测水力裂缝的方法有主动声波监测和被动声波监测2种：被动声波监测法具有随机性强和声波数据处理量大等缺点；主动声波监测法易受天然裂缝和井壁干扰，传感器的布置方式也会影响监测精度。主动声波监测法可以监测裂缝在最大应力平面内的扩展，但无法解释三维空间裂缝转向的问题[8]。利用电磁法监测水力裂缝方位的最大优势是可以注入导电性支撑剂，用支撑剂指示方位信息。目前利用声波和微地震监测到的裂缝方位信息稍显不足。

为研究上述问题，笔者以电磁场理论为基础，基于有限元软件平台，建立了直井的三维地层与裂缝几何模型，并利用有限元法对裂缝模型进行正演模拟计算。在此基础上，对测井仪器上多个接收线圈得到的感应电动势的振幅和相位进行了深入研究，探讨了裂缝模型的响应情况；然后，分析了测井曲线随裂缝长度、高度，支撑剂电导率及裂缝与井眼之间角度的变化规律，进一步分析了测井仪器对水力裂缝探测的影响，为水力压裂效果评价及测井仪器参数选择提供了理论依据。

1 解析模型的建立

1.1 时谐电磁场理论

由于电磁波测井仪的发射线圈使用交流电来产生电磁波，所研究的电磁场是时谐场。也就是说，电磁波的振幅和相位随时间呈正弦或余弦变化。因此，选用微分方程组来求解[9-13]，即：

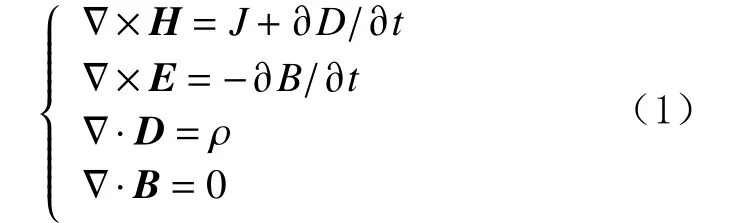
用复相位因子表示法，式（1）可以简化成:

式中：σ为媒介的电导率，S/m；ω为发射源角频率，rad/s；ε为介电常数，F/m；为发射■线圈上外加电流密度，；μ为磁导率，H/m；。

1.2 边界条件

求解麦克斯韦方程的关键是选择合理的边界条件[14]，边界条件与界面两边的电磁场有关。笔者主要考虑理想导体边界条件、发射线圈边界条件和阻抗边界条件。

1）理想导体边界条件。从理论上讲，任何边界处的电场强度切向分量和磁场强度法向分量是连续的[15]。因此，电场强度的切向分量和磁场强度的法向分量不可能在理想导电体的表面上，其表面上只能存在电场强度法向分量和磁场强度切向分量。即理想导电体表面上的边界条件为：

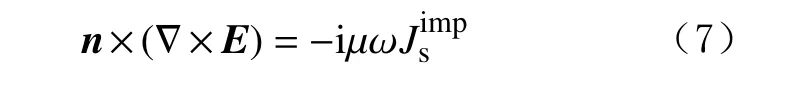
3）阻抗边界条件。阻抗边界形成于2个不完全导体的介电界面上。非理想导体具有损耗和电阻，因此阻抗边界条件为：

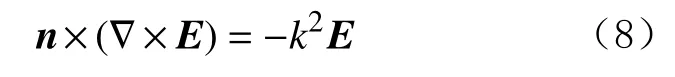
假设在均质各向同性介质中，接收线圈R1的电动势为，接收线圈R2的电动势为。根据式（6）、式（7）、式（8）和式（4）求得接收线圈 R1和 R2的感应电动势和：

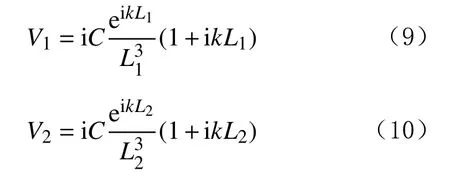
式（13）和式（14）为电磁波信号振幅比和相位差的解析表达式[17-18]。

2 解析模型可行性验证

笔者所建地层模型为100 m×100 m的均质各向同性地层，不考虑井眼和钻铤的影响，采用单发双收电磁波测井仪。假设发射线圈电流幅度为1 A，发射频率为400 kHz，源距离L1和L2分别为1.00和1.20 m，相对磁导率为1，发送线圈和接收线圈的匝数均为100匝，线圈半径为0.03 m。利用有限元软件求得均匀各向同性地层振幅比和相位差与地层电导率之间的关系曲线，并与式（13）和式（14）的计算结果进行对比，结果如图1。

从图1可以看出：利用有限元软件模拟求得的曲线与利用式（13）和式（14）计算出的曲线基本重合；当地层电导率小于1 S/m时，随着地层电导率增大，振幅比增大缓慢；当地层电导率大于1 S/m时，振幅比快速增大；随着地层电导率增大，相位差均匀增大。模拟计算结果与解析计算结果高度一致，验证了解析模型的正确性。

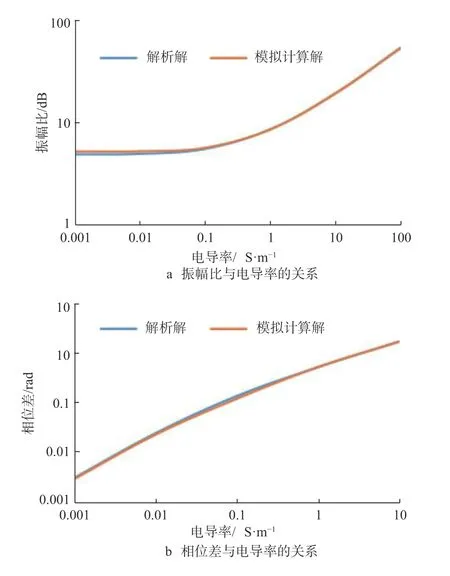
图 1 均质各向同性地层振幅比和相位差与地层电导率的关系曲线Fig.1 Relationship between amplitude ratio and phase difference in a homogeneous and isotropic formation

3 裂缝模型正演算例

在实际测井时，垂直井眼周围分布着大量的不规则裂缝。笔者旨在研究电磁波测井探测水力裂缝的正演效果，暂不考虑多条裂缝同时存在的情况。水力裂缝模型采用裂缝长度远远大于裂缝高度的形式。假设仪器发射线圈为T，两个接收线圈分别为R1和R2。发射线圈T与接收线圈R1和R2之间的距离分别为L1和L2（L2＞ L1）。为了更好地检验电磁波测井的实用性，采用不规则裂缝模型，其剖面如图2（a）所示。采用四面体进行网格划分，结果如图2（b）所示。假设不规则裂缝为1条，位于地下50.00 m处。电磁波测井仪参数：发射频率为400 kHz；源距L1为1.00 m、L2为 1.20 m；发射线圈 T 的匝数为 100匝、半径为0.03 m；线圈中的电流为1 A。裂缝模型参数：地层电导率为0.1 S/m，裂缝电导率为200.0 S/m，裂缝相对最长处为15.00 m，裂缝相对最高处为1.00 m。

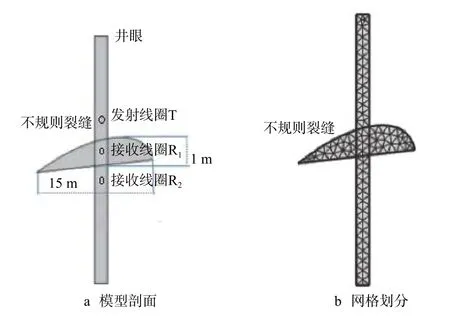
图 2 不规则裂缝模型及网格划分Fig. 2 Irregular fracture model and meshing

利用有限元软件并结合式（13）和式（14），计算不同位置处的振幅比和相位差，结果如图3所示。

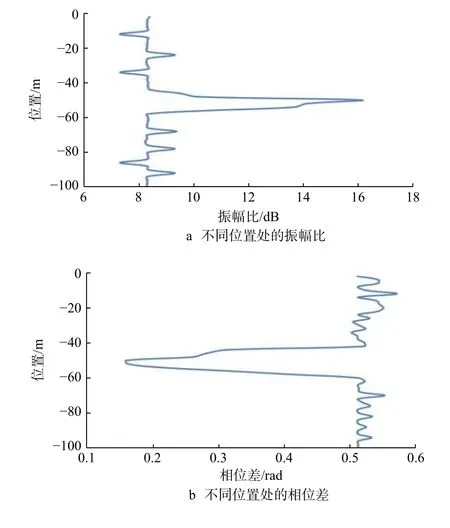
图 3 不同位置处的振幅比和相位差Fig. 3 Amplitude ratio and phase difference at different positions

从图3可以看出：尖峰现象明显，且峰值位于距离地面50.00 m处，与理论位置一致；振幅比和相位差曲线在-50.00 m位置附近处的波形不规则，此现象应与裂缝形态具有一定的相关性。虽然出现一部分小的干扰曲线，但不影响正演模拟结果。这表明，电磁波测井适用于横截面为不规则图形的裂缝模型，可以准确正演出裂缝位置。

4 影响因素分析

4.1 水力裂缝敏感性分析

采用控制变量法研究裂缝高度、支撑剂电导率、裂缝长度和裂缝与井眼之间不同角度对电磁波测井仪探测结果的影响。选取垂直于井眼的横切面为椭圆形的单一裂缝进行分析。假设单个椭圆形裂缝位于地下50.00 m处，电磁波测井仪参数：发射频率为 400 kHz；源距 L1为 1.00 m，L2为 1.20 m；发射线圈匝数为100匝、半径为0.03 m；发射线圈电流为 1 A。模型参数：地层模型范围为 100 m×100 m，相对磁导率为1。

4.1.1 裂缝高度

设地层与钻井液的电导率为0.1 S/m，裂缝电导率为100.0 S/m，裂缝长度为50.00 m。在地层和裂缝电导率不变的情况下，裂缝高度h 依次设为10.00，5.00，2.00，1.50，1.00 和 0.50 m，计算不同裂缝高度下的振幅比和相位差，结果如图4所示。

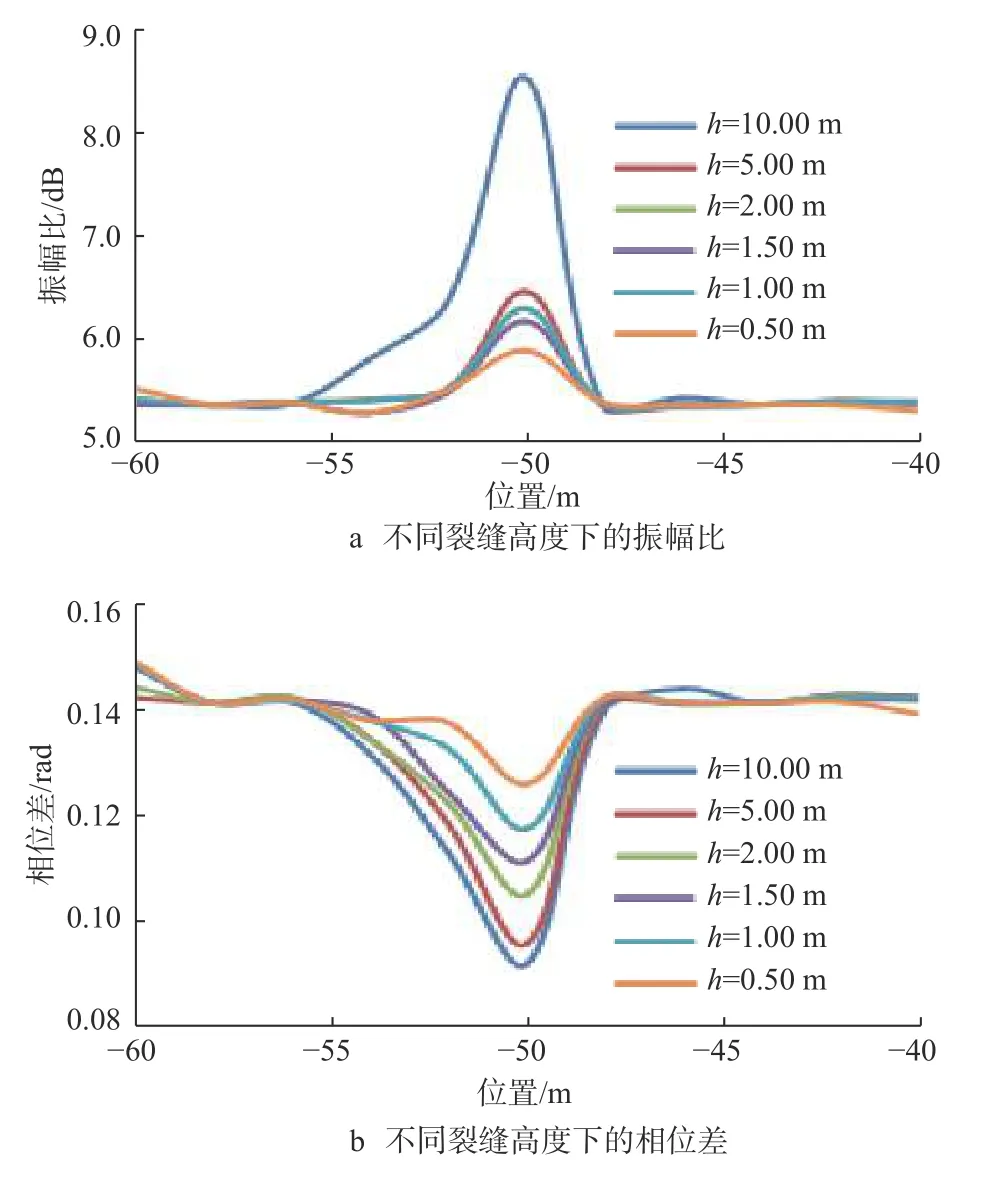
图 4 不同裂缝高度下的振幅比与相位差曲线Fig.4 Amplitude ratio and phase difference at different fracture heights

从图4可以看出：裂缝高度对于振幅比影响较大，当电磁波测井仪靠近裂缝时，裂缝高度越大，尖峰现象越明显；裂缝高度对于相位差影响较大，当电磁波测井仪接近裂缝时，尖峰现象更加明显。对比不同裂缝高度下的振幅比与相位差发现，相位差分层现象明显，更容易通过其分辨不同高度的裂缝。

4.1.2 支撑剂电导率

向裂缝中注入含有高导电性的支撑剂可以增加裂缝的电导率。假设裂缝高度为0.50 m，长度为20.00 m。假设支撑剂电导率 σz分别为 50，100，150，200，50和300 S/m，高导电性支撑剂均匀填充于水力裂缝。在地层电导率、裂缝长度及高度不变的情况下，计算不同电导率支撑剂下的振幅比和相位差，结果如图5所示。

图 5 不同电导率支撑剂下的振幅比与相位差曲线Fig.5 Amplitude ratio and phase difference for different electrical conductivity of proppant

由图5可知：含有高导电支撑剂裂缝的振幅比高，尖峰现象明显；随着支撑剂电导率增大，相位差减小，尖峰现象越来越明显；支撑剂电导率对振幅比的影响较小，对相位差的影响较大。相位差曲线可以更好地反映含有不同电导率支撑剂裂缝的信息，可以通过其更好地分辨不同电导率的裂缝。

4.1.3 裂缝长度

假设裂缝高度为0.10 m，支撑剂和地层电导率分别为200和0.1 S/m。在裂缝高度、地层和支撑剂电导率不变的情况下，计算裂缝长度Lf为0，1.00，10.00，50.00和100.00 m时的振幅比和相位差，结果见图6。

图 6 不同裂缝长度下的振幅比与相位差曲线Fig.6 Amplitude ratio and phase difference at different fracturelLengths

由图6可知：随着裂缝长度增加，振幅比增大，尖峰现象越来越明显；随着裂缝长度增加，相位差减小，尖峰现象越来越明显。

4.1.4 裂缝与井眼夹角

假设地层与钻井液电导率为0.1 S/m，裂缝电导率为100.0 S/m，裂缝轴对称中心点位于地下50.00 m处，裂缝长度为20.00 m、宽度为0.10 m。计算裂缝与井眼的夹角 α 分别为 30°、45°、60°和 75°时的振幅比和相位差，结果如图7所示。

从图7可以看出：当裂缝和井眼的夹角为45°、60°、75°时，振幅比与相位差曲线的尖峰现象明显且呈现一定的规律，当裂缝和井眼夹角为30°时，尖峰现象出现偏差；随着裂缝和井眼夹角增大，振幅比减小，相位差增大。综上所述，裂缝和井眼的夹角在30°～90°时，正演响应较为明显。

4.2 电磁波测井仪敏感性分析

4.2.1 仪器源距

选用单一的椭圆形裂缝模型进行计算分析。假设裂缝位于地下50.00 m处，裂缝长度为20.00 m、宽度为0.50 m，地层与钻井液电导率为0.1 S/m，裂缝电导率为 100.0 S/m，发射频率为 400 kHz，发射线圈匝数为100匝、半径为0.03 m，线圈中的电流为1 A，接收线圈间的间距为0.20 m，计算发射线圈与接收线圈距离 l为 0.25，0.50，0.75，1.00，1.25 和 1.50 m 时的振幅比和相位差，结果如图8所示。

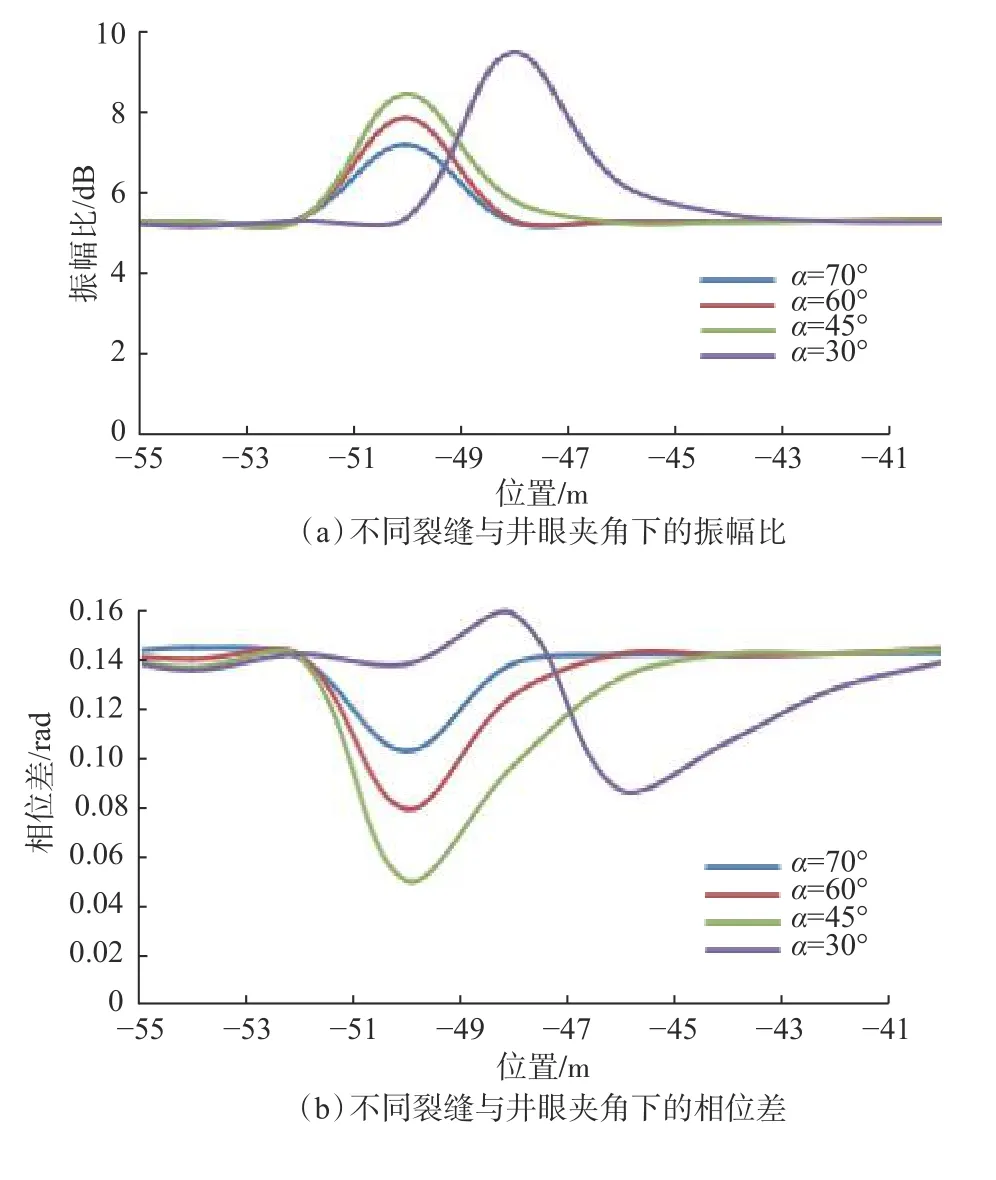
图 7 不同裂缝与井眼夹角下的振幅比与相位差曲线Fig. 7 Amplitude ratio and phase difference with different included angles between the fracture and borehol

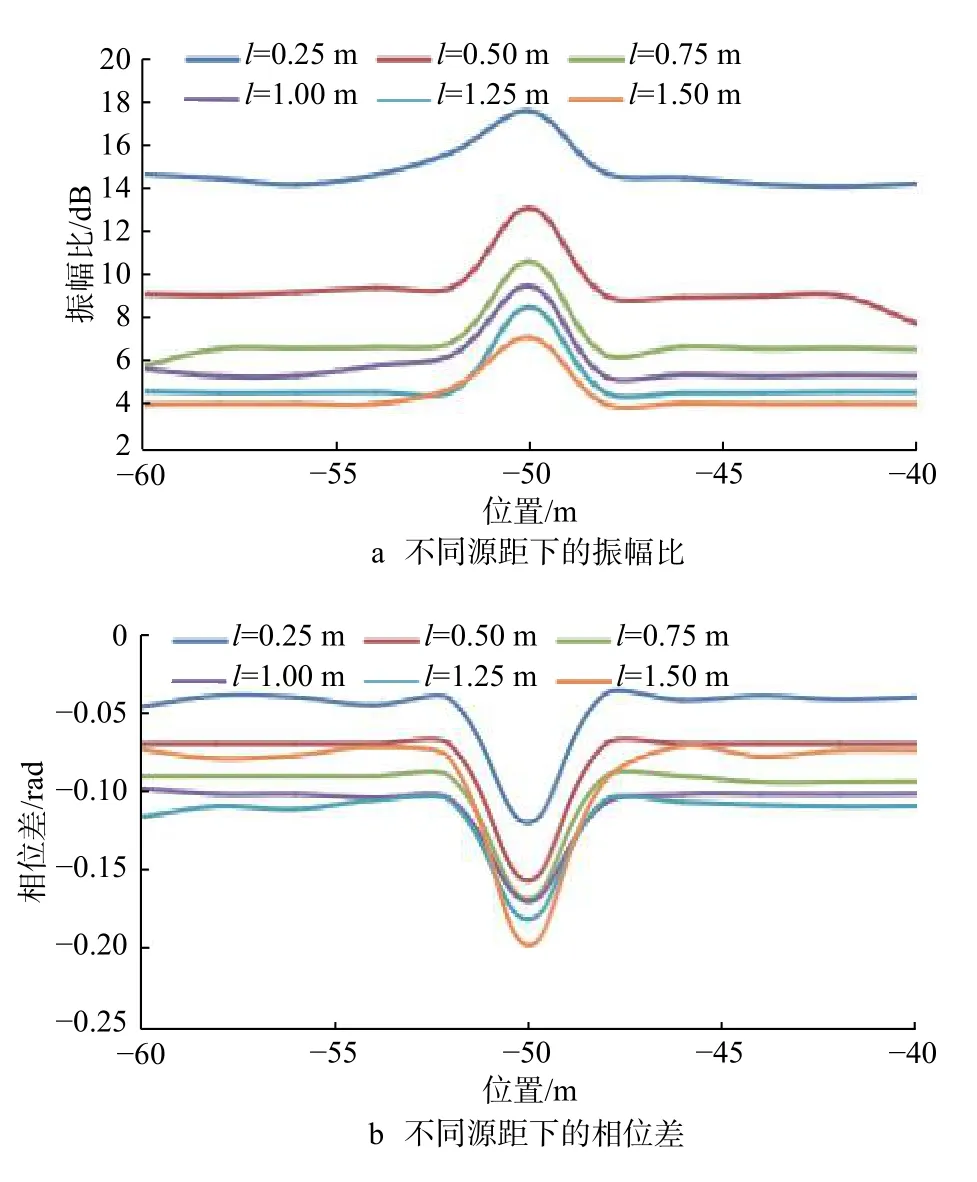
图 8 不同源距下的振幅比与相位差曲线Fig. 8 Amplitude ratio and phase difference at different source distances

由图8可知：振幅比与相位差曲线的尖峰现象明显；随发射线圈与接收线圈距离增大，振幅比和相位差减小。所以，在电磁波测井时，应优先选择发射线圈与接收线圈距离较近的电磁波测井仪，以获得更好的探测结果。

4.2.2 发射频率

假设地层与钻井液电导率为0.1 S/m，裂缝位于地下50.00 m处，裂缝电导率为100.0 S/m，裂缝长度为20.00 m、宽度为0.50 m，发射线圈匝数为100匝、半径为0.03 m，线圈中的电流为1 A，接收线圈间的距离为0.20 m，发射线圈与接收线圈的距离为1.00 m，计算发射频率 f为 400 kHz，1.0，1.5 和 2.0 MHz 时的振幅比和相位差，结果如图9所示。

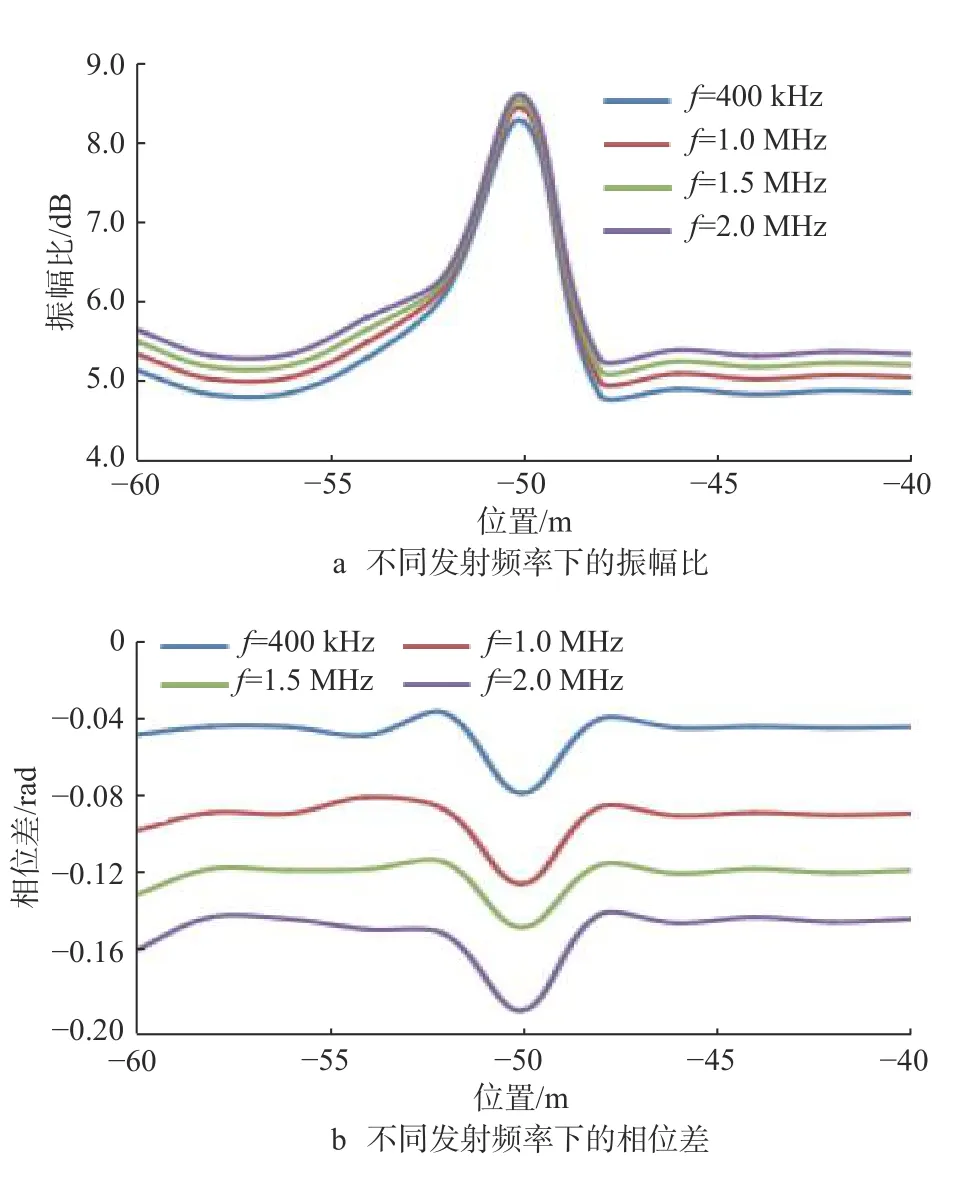
图 9 不同发射频率下的振幅比与相位差曲线Fig.9 Amplitude ratio and phase difference at different transmitting frequencies

由图9可知：随着发射频率增大，振幅比增大，但增大幅度较小，不同发射频率下的振幅比曲线不易区分；随着发射频率增大，相位差减小，且减小幅度较大，发射频率为400 kHz时的相位差峰值最大。

5 结论及建议

1）采用有限元算法建立了电磁波测井仪器与地层模型，利用电磁波测井探测直井水力裂缝的正演模拟具有较高的准确性。正演模拟结果对于识别裂缝位置等信息、判断裂缝的有效性、确定裂缝系统区域的有效性具有一定的参考价值，有利于找到油气储层。

2）采用控制变量法分析了裂缝高度、长度，支撑剂电导率，裂缝与井眼夹角对电磁波测井响应的影响。相位差曲线分层明显，通过相位差曲线可以分辨不同高度及含不同电导率支撑剂的裂缝。对电磁波测井响应影响最大的因素为支撑剂电导率，其次为裂缝高度与长度。

3）电磁波测井时，应优先选择发射线圈与接收线圈距离较近的电磁波测井仪，以获得更好的探测结果。

4）本文只是对直井水力裂缝正演进行了定性分析，建议结合油田的实际情况和测井资料，根据实际地质条件，与油田的实际测井资料进行比较，进一步优化电磁波测井仪结构，并进行正演模拟，以建立适合我国地层的测井解释资料数据库。