基于时变参数-SIR 模型的COVID-19疫情评估和预测

喻 孜，张贵清，刘庆珍，吕忠全

(1. 南京林业大学理学院 南京 210037；2. 天津科技大学理学院 天津 滨海新区 300457；3. 中国医学科学院血液病医院 天津 和平区 300020)

截至2020 年1 月31 日晚12 点，全国确诊新型冠状病毒肺炎(COVID-19)病患接近1 万。政府迅速采取了一系列措施来对抗疫情。从2020 年1 月23 日开始，地方政府陆续开始“封城”并通过媒体实时发布确诊人数、专家通过网络及媒体传播防治疫情的注意事项、全社会自觉在家自我隔离、戴口罩出门、企业延期复工及人员聚集场所关停等。疫情的发展已经严重影响到人们的日常工作与生活，并逐渐开始产生恐慌情绪。全社会都在关注两个重要问题：一是确诊人数将如何变化，什么时候会下降？二是迄今为止，政府所采用的防控措施，产生了多大的积极作用？回答这两个问题，需要对疫情进行科学的预测和评估。

目前已经有大量工作对COVID-19 疫情进行了研究。文献[1]根据最早425 例确诊病例数据，描述了病例特征，并估计了关键流行病学延迟时间分布情况，在病毒早期呈指数增长的初期，估计了传染病倍增时间和基本再生数。文献[2]发现了第二代病例，指出病毒会存在“人传人”，对金银潭医院最开始收治患者时候的信息进行归纳研究，指出非华南海鲜市场暴露的病例的存在。文献[3]基于SEIR 模型，根据2020 年1 月25 日之前的发展趋势，估算得到了COVID-19 的再生数，并对疫情发展进行了预测。还有很多其他研究[4-9]，从不同角度对疫情的特点进行了评估。这些研究都对疫情的防治提供了重要的参考。在病毒传播研究中[10-13]，由于SIR 动力学模型能给出较为清晰的逻辑关系和准确的趋势预测，因而被广泛采用。相比于之前的病毒传播事件，COVID-19 疫情比较特殊：1) 相对于总的人口基数，目前的治愈人数和死亡人数都较低，因此出院人员(removed)比率可以忽略不记；2) 从2020 年1 月11 日，官方开始报道确诊人数以来，存在人口流动，因此传统SIR 模型认为总体环境是封闭(S+I+R=常数)并不符合现实；3) 由于染病确诊后将被隔离，所以确诊病人并不形成新的感染；4) 此次病毒有较长的潜伏期，会带来明显的延迟效应；5) 此次疫情突发，诊断力量在初期存在明显不足。综上所述，为了更为准确地对疫情进行预测，需要对SIR 模型进行修正。本文根据实际情况，对SIR 模型进行了适当修正，聚焦国内确诊人数的变化，对趋势进行预测和判断，并根据结果对现有政策进行评估。

1 模型

本文根据实际疫情对SIR 模型进行了一些修正，描述如下：

1) 由于不存在封闭情况，考虑开放体系。

2) 新型冠状病毒的治愈人数和死亡人数相对较小，因此只考虑Susceptible(易感)和Infected(感染)两类人群。

3) 目前数据以天为单位发布，因此不考虑连续变化情况，只考虑离散的方程。

4) 当确诊后，病人立即隔离，因此不会作为新的感染源。因此感染源应该是第n+1 天和第n 天诊断的病人差。假设平均染病者(I)会使k 个人成为易感者(k 为易感再生数)，则每日新增的感染者为k(In+1−In)。

5) 假设每天有 µ1的概率(当日感染率)易感者会成为感染者，则当日新增病人为 µ1Sn。 其中 kµ1，描述了当日病人再生数，后文简称当日再生数。

6) 病情会有约10 天的潜伏期，在初期出现症状后，很多暴露者才会去寻求诊断，同时主要发病地武汉的初期诊断能力有限，这都会带来一个延迟效应。取τ=4，代表平均延迟天数。在平均4 天内的潜伏者会以 µ2的概率(潜伏感染率)被确诊为感染者。则每日潜伏感染人数为 µ2(Sn−Sn−τ)。 kµ2描述了由于潜伏原因导致的病人再生数，后文简称潜伏再生数。

基于上述考虑，在每日模型迭代中，各部分更新关系如下：

为了求解式(1)，需要知道(k, µ1, µ2)3 个模型参数[14-18]，以及I 和S 的初值。I(0)通过官方数据给出(数据来源于官方网站：http://www.nhc.gov.cn/)，剩下3 个参数以及S(0)则没有信息。本文先给定3 个参数和S(0)的初值，求解方程，将得出的解与真实数据进行比较，通过梯度下降法寻找方差的最小值，从而确定模型参数。由于梯度下降法对初值极为敏感，因此，本文还根据经验在一定初值范围内进行多次搜索，保证得到的是最优解。

模型参数(k, µ1, µ2)是根据一个阶段的数据求出，因而能够反应病毒在该阶段的传播趋势。通过截取不同阶段的数据来求解不同阶段的(k, µ1,µ2)，就能分析病毒演化趋势是否在外力作用下发生改变。最后再通过模型参数(k, µ1, µ2)的变化规律，对未来进行预测。

官方从2020 年1 月11 日开始公布数据，前4 天均无确诊人数变化。本文选择2020 年1 月15 日作为数据研究的起始点，然后变化数据的结束点来截取不同时间段的数据进行求解。为了描述方便，后文对时间段使用结束日期的英文简写来标识。例如1 月15 日至1 月24 日这个时间段，简称为Jan.24th 时间段，1 月15 日至1 月28 日这个时间段，简称为Jan.28th 时间段。Jan.24th 时间段是文章研究的第一个时间段，此后每增加1 天构成一个新的时间段。这是基于以下两点考虑：1) 从Jan.24th 时间段开始，已经积攒了足够多的数据(10 天的数据)；2) 政府从1 月11 日开始公布确诊人数并采取措施，趋势的形成需要一个时间，并且病毒的最长潜伏期约为14 天。需要指出，在理想状况下，S(0)应该是一个确定值，然而，在开放体系下，通过现有的数据无法评估S(0)的真实值。因此只能通过式(1)的解与数据拟合来反向求解S(0)。这会造成不同阶段的S(0)略有不同。然而，由于本文采用了大范围梯度下降搜索，因此每一组参数都是在与现有数据拟合最优情况下得到的，因此文章求解得到的(k, µ1, µ2)能体现数据背后隐藏的病毒演化趋势。

2 模型参数的影响

2.1 易感再生数、当日感染率、潜伏感染率的影响

图1～图3 给出了不同时间段的拟合效果，其中曲线是模型计算结果，圆点代表官方统计数据。从图中发现模型的计算结果和实际公布的数据吻合较好，说明模型是合理的。同时也发现易感再生数、当日感染率、潜伏感染率参数也确实发生了变化，并且是在不断减小，这和政府的防控措施及民众的居家防护有直接关系。图4 给出了3 个时间段确诊人数随时间变化的趋势图。从图中可以清楚发现，疾病的传播趋势确实是在减缓的，如果按照Jan.24th 时间段的疫情发展趋势，那么在2020 年1 月31 日的确诊人数将会达到近40 000，同样，如果按照Jan.28th 时间段的疫情发展趋势，那么1 月31 日的确诊人数将会达到15 000 左右，明显高于实际疫情的发展情况。所以图4 表明政府的防控措施和民众的居家防护对于疫情的控制确实效果明显(确诊人数按照趋势变化减少了将近1/2)。

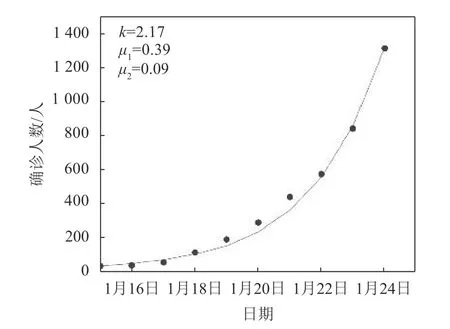
图1 Jan.24th 时间段的拟合效果图

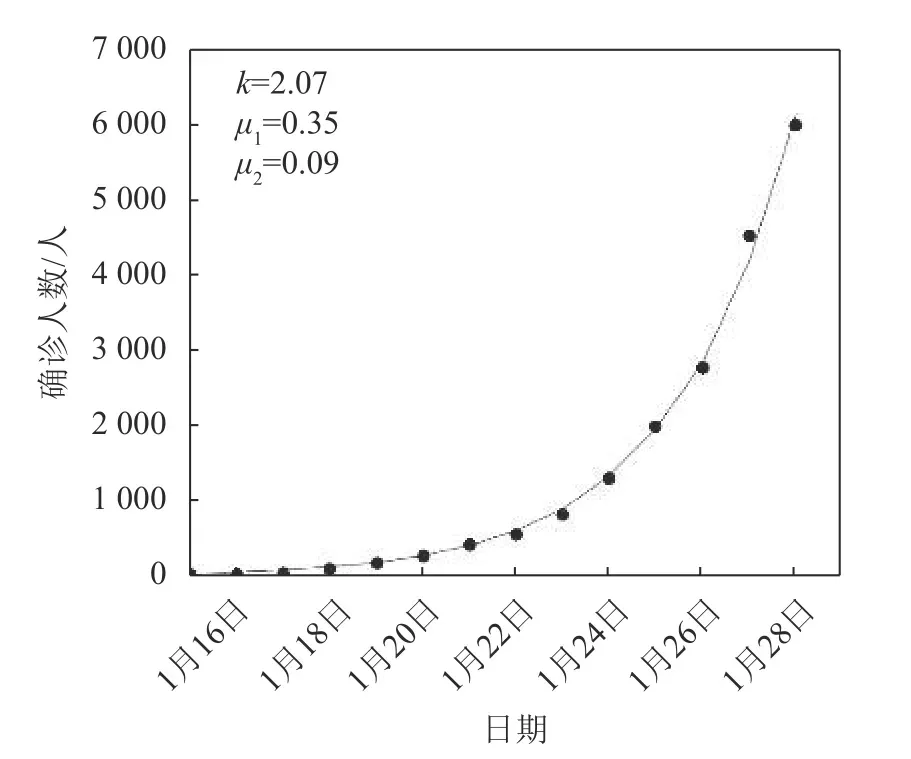
图2 Jan.28th 时间段的拟合效果图

图3 Jan.31th 时间段的拟合效果图

图4 不同时间段确诊人数的走势图

2.2 易感再生数、当日再生数、潜伏再生数的变化趋势

为了更清楚地展示从初始阶段(Jan.24th 时间段)起的趋势变化情况，本文从第一个阶段(2020 年1 月15 日−1 月24 日)开始，每增加一天构成一个新的时间段进行求解，得到了易感再生数、当日感染再生数和潜伏感染再生数随时间的演化趋势。结果如图5～图7 所示，图中的横坐标代表了时间段结束日期，图中x 的值取时间段结束日期与1 月23 日间隔的天数(例如1 月24 日对应x=1，1 月25 日对应x=2)。从图中可以看到3 个参数都有下降趋势。同时，趋势每天都在改变。说明政府的防控措施和民众的居家隔离确实产生了强力效果。需要注意，2020 年1 月27 日，多地医疗工作者驰援武汉，使得检测能力得到大幅提升，所以导致1 月27 和28 日的确诊人数大幅上升，出现了明显的和前期不一样的易感再生数、当日再生数和潜伏再生数。这些参数的波动，也从侧面证明了本文模型能够敏感地体现外力对趋势的改变。另一方面，也说明参数固定不变的动力学模型无法真实体现此次 COVID-19 疫情的变化情况。

图5 易感再生数随着时间的演化情况(去除了27 日的波动较大点)

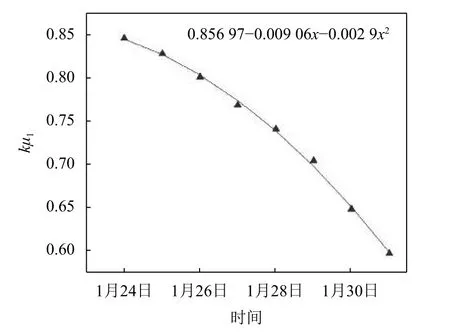
图6 当日再生数随着时间的演化情况

3 基于最优参数的疫情预测

为了结合现有趋势对未来进行预测，本文去除波动数据的影响对参数进行了拟合，从而得到了参数的变化趋势方程如下：

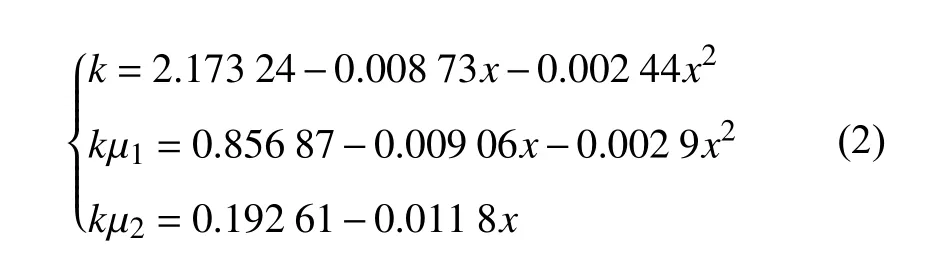
式中，x 代表与1 月23 日间隔的天数，从1 月24 日开始取1。参数按照式(2)的规律变化，代入式(1)中进行求解，预测1 月31 日以后的数据，如图8 所示。从图中可以看出26 天后，也就是2020 年2 月9 日左右应该会出现确诊总数的峰值，同时确诊人数也达到最大的54 000 左右。随后确诊人数将会下降。

图7 潜伏再生数随着时间的演化情况(去除27，28 日上下两个波动点后，发现直线拟合效果最佳，因此用直线拟合)

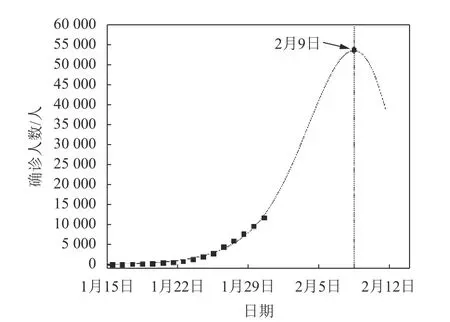
图8 图中给出了在模型最优参数条件下的模型估计值

4 结 束 语

本文基于修正SIR 模型研究了COVID-19 疫情发展到2020 年2 月1 日(政府隔天公布数据)为止的趋势和政策的效果。模型的参数根据实时数据拟合得到，因而修正过后的时变参数-SIR 模型结果能够反应不同阶段疫情的趋势变化。通过趋势变化能够解读政府的防控措施产生的效果。结果表明，在2020 年1 月27 日和28 日，由于全国医疗系统驰援武汉使得确诊能力得到了增强，一些积压和潜伏病人得到收治，因此模型参数出现扰动。其他时间段，参数变化趋势明显。2020 年1 月24 日之后，政府的的防控措施有效地降低了病毒蔓延趋势，使得染病人数的变化趋势逐日下降。易感再生数、当日感染率和潜伏感染率都大幅度降低。基于当前的趋势对疫情发展进行了预测。结果表明，在2 月9 日左右，疫情会达到高峰，随后确诊人数将会出现下降。

从动力学方程的解和实际数据的比较来看，本文提出的时变参数-SIR 模型能够及时反应现有趋势变化，甚至体现一些突发情况(2020 年1 月27 日全国医疗系统驰援武汉)带来的影响。因此，本文基于现有数据对趋势变化的分析结论应该是有效的。从预测角度来说，动力学预测方案本身就会存在一定的不确定性。然而，本文并没有采用固定参数去求解动力学方程，而是基于前期积累的趋势，采用动态参数求解，这在一定程度上减少了动力学方程的不确定性。因而，本文预测的趋势应该能够提供有益的参考价值。本文基于COVID-19 病毒的流行特点，对SIR 模型进行的理论修正，以及通过数据确定动态参数进行预测的方案，会对病毒的研究提供积极的理论参考。

本研究工作还得到天津科技大学青年教师创新基金(2014CXLG23)的资助，在此表示感谢。