基于目标运动的复眼式双目视觉测距法

高文静，杨预立，邢 强，徐海黎

（南通大学 机械工程学院，江苏 南通 226019）

引言

根据两眼视网膜上不同视图场景目标估计目标深度的方法被称为立体视觉[1-3]。立体视觉的研究一直是机器视觉中的重点和难点，常见的立体视觉研究大都利用多个光学传感器获取目标信息进行目标定位。根据应用需求，研究人员搭建了相应的双目视觉系统，如满足大测量范围和高精度需求的稳定平台固定型双相机立体视觉系统[4]，以及满足固定小视野范围高速实时测量的单相机立体视觉结构[5]。目前，在双目立体视觉系统的研制中，选用相机的视角、焦距以及双目结构中各相机间的基线长度都对双目立体视觉的检测精度有很大影响。固定结构下，相机视角、焦距以及相机间基线越小，测量范围越小，测量精度越低[6]。目前的目标检测算法大都基于对图像特征的处理，在处理复杂环境中的运动目标时，连续采集图像序列，进行图像特征配准得到目标运动状态。这类算法计算数据量大，定位实时性低，且对每一时刻采集的静态图像作目标检测时，若运动目标与背景之间差异性较小，则特征匹配类算法对目标区分检测困难，检测精度较低[7-9]。与人眼相比，昆虫复眼具有多个小眼组成的多通道视觉系统，各小眼在结构上呈球面分布，构成近360°的大范围视野。各小眼单独处理目标信息，具有空间分辨率较低、信息处理速度快、时间分辨率高等优点[10-11]，可以快速获取大视场范围内的场景信息，从而发现目标[12]。由于复眼结构具有特殊性，与人的立体视觉不同，复眼昆虫不是简单使用双目视差来实现捕食避障。复眼昆虫可以获得运动目标在微小时间内的视觉信息变化，在目标运动时，各小眼单独成像到视网膜上获得连续变化的目标信息，通过神经系统分析这种动态信息来实现导航定位[13-14]。如复眼昆虫螳螂就是根据双目对目标运动模式的匹配及运动视差来实现目标识别与距离判断的，即使目标与背景差异性较小，也可通过场景中物体的运动特征来实现目标与场景的区分，以实现捕食和避障行为[15-16]；蜜蜂等飞行类复眼昆虫通过对比双目检测场景中物体运动产生的光流信息实现飞行导航，即使双目检测的场景差异性较小，也可通过对比两侧场景的运动快慢进行距离估计，调整飞行轨迹[17-18]。与基于图像检测的特征法相比，基于运动模式的目标定位算法不需要匹配特征点，避免了很多计算量以及目标与场景差异性较小导致的特征误匹配问题，节省了计算时间，提高了实时性[19-21]。目前，光流法是常用的运动目标检 测 算 法，经 典 光 流 算 法 由Hom & Schunck 于1981 年提出，假设目标运动速度场平滑，结合光流约束方程计算得到运动目标的光流场，是目前使用最多的方法之一[22]；Nagelp 在考虑目标遮挡问题下采用平滑约束，利用二阶导数计算光流场，但二阶导数计算不稳定易受到噪声影响[23]；Srinivasan提出了用于运动图像检测目标的光流法，该方法根据图像中目标像素点与周围像素点之间的变化来估计目标的运动状态[24]。

根据仿复眼多通道视觉系统的目标检测特性，启发于复眼昆虫可以利用运动目标的动态光流信息实现对目标的准确定位，本文提出一种基于光流原理的多通道环形视觉传感器的目标方位角快速检测算法。首先以光电传感器为子传感器研制环形360°的视觉传感器；其次基于目标在环形传感器阵列中连续获得的系列目标信号分布，提出基于光流原理的目标方位角快速检测法；最后基于双目测距原理，实现两环形视觉传感器在大视场范围内对与传感器排列垂直面内的目标测距。该方法适用于多通道组成的视觉系统，对运动目标前后两时刻的传感器信号进行连续计算获得目标位置，避免了多通道视觉传感器在每一时刻对目标信号作定位算法处理，有效提高定位速度，为立体视觉快速测距提供了一种简单快速的方法。

1 基于运动模式的目标方位角检测模型

生物复眼具有检测光流的功能[25]，在一定的序列信号中，计算运动目标前后两时刻在传感器中的信号变化，从而获得目标运动状态的算法被称为光流法。受此启发，本文提出了一种基于光流的目标运动检测方法。

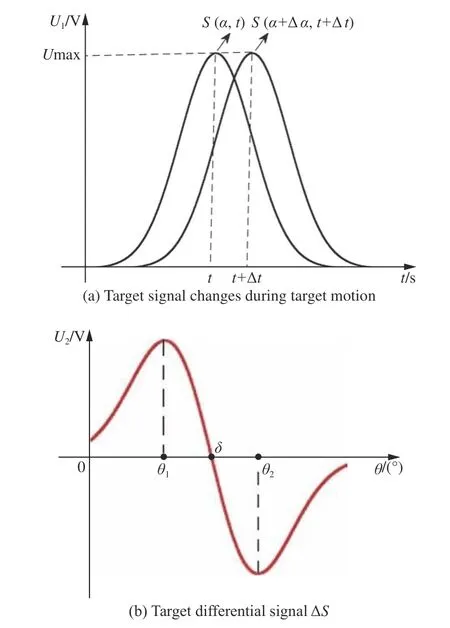
图 1 运动目标方位角检测原理Fig. 1 Schematic diagram of moving target azimuth detection

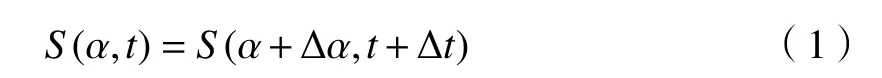
将（1）式右边用泰勒公式展开得：

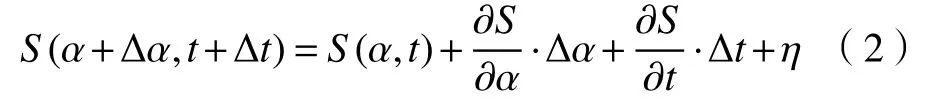
忽略二阶以上高阶项后，代入（1）式得：

本文提出的目标检测模型使用前后两时刻采集的目标原始信号计算目标角度，这种测量算法计算数据量小，算法简单快速。但也存在误差，误差的性质与静态测距每次检测存在误差一样，不是对检测结果的依次叠加运算，即每次测量虽存在误差，但误差之间是独立的。

2 实验装置与方法

2.1 实验平台

确定目标方位角的环形运动视觉传感器检测平台主要由环形传感器阵列、目标运动装置和多通道数据同步采集装置组成，如图2 所示。检测平台放置于工作台上，工作台的重量远比运动模块的重量大得多。工作台表面为橡胶材质，且检测平台下方放置泡沫塑料以减少电机带动运动模块时产生的振动。运动装置正常工作时，平台产生的抖动很小，传感器检测稳定。

图 2 环形传感器示意图与实验装置Fig. 2 Schematic diagram of ring sensor and experimental device

目标运动装置主要用于实现目标在二维平面内的直线运动。主要由运动控制卡（AMP208C，凌华，中国）、步进电机、同步轮同步带、拉线编码器（millayWXY10 拉 线 编 码 器，精 度 为0.02% full scale）以及目标（2 mm CCFL 柱光源）等组成。该运动模组通过运动控制卡与同步轮同步带，可实现目标在平面内最大速度为80 mm/s、最大加速度为20 mm/s2的直线运动。

多通道数据采集模块主要由环形传感器阵列、电压转换模块、数据采集卡（PCI1747U，研华，中国）等组成。其中，启发于复眼的小眼排列结构的环形传感器阵列由按ψ（ψ=6°）等夹角环形排列的N（N=60）个子传感器及半径为R（R=75 mm）的环形固定结构组成，安装于旋转平台上；电压转化模块用于放大和稳定传感器输出电压，并将信号传输给上位机数据采集卡处理。上位机Lab View（Nation Instrument，美国）程序实现128 通道采样率1 000 Hz 的数据同步采集。

2.2 实验步骤

为了实现对目标方位角检测以及目标测距，利用上述实验平台，设计了在一定测量范围内环形传感器对目标方位角检测与标定以及双目传感器阵列的立体视觉测距实验，如图3 所示。

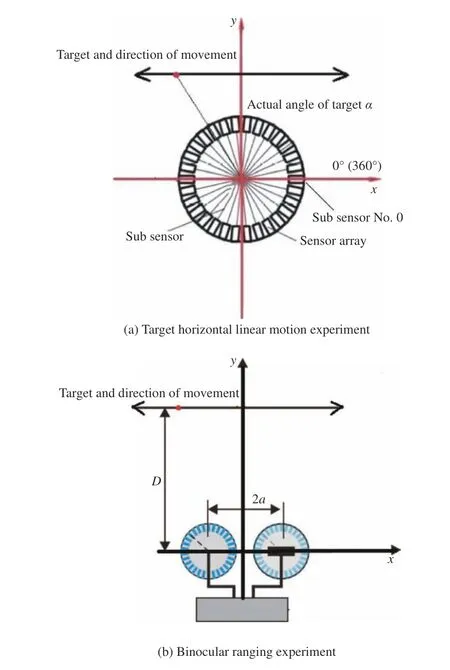
图 3 目标运动实验图Fig. 3 Experimental diagram of target motion

按图2 搭建实验平台，同轴安装旋转平台与环形传感器阵列，以环形传感器阵列圆心所在处为原点建立图3（a）所示的二维平面直角坐标系进行目标方位角的确定以及测距实验操作。具体步骤为：1） 调整安装位。取某传感器为0 号子眼，调整其视轴方向与x 轴正向（0°线）重合，在离传感器中心垂直距离D 处安装目标（柱光源）。2） 数据采集。实验环境在无目标时，传感器阵列采集环境信号值在0.065 V 左右；在实验范围内，传感器检测的目标信号范围为0.5V～4 V，目标强度远大于环境强度，其中最大目标信号值对应的子传感器位置作为目标方位角检测的参考位置以实现目标位置检测[11]。基于运动视觉的环形传感器对目标方位角的确定以及测距实验主要是：①采集与环形传感器中心垂直距离为D、目标在传感器视野范围内作直线运动时的各子传感器信号，其中规定编号为0 的子传感器视轴方向角度为0°，如图3（a）所示；②按图3（b）搭建实验平台，将两个环形传感器安装在基线为2a 的平台上，以基线中点为原点建立右手螺旋直角坐标系，搭建双目视觉传感器。驱动目标运动装置，在目标运动的同时，传感器采集目标信号数据传至上位机程序，利用方位确定算法实现运动目标方位角检测，再利用三角视差原理实现双目视觉传感器在2D 平面内对运动目标的快速测距。3） 数据处理。传感器检测的目标信号形式为各子传感器检测信号组成的一维信号，利用Lab View 软件中的5 阶巴特沃斯（Butterworth）低通滤波、smooth 平滑滤波的方式实现传感器阵列采集目标信号数据的平滑，剔除传感器信号的异常值，实现目标信号数据的预处理；利用方位角检测模型分析多通道视觉传感器相邻时间采集的目标信号，计算出目标角度δ（称为测量角度δ），采用 Mat Lab 软件分析拉线编码器记录的目标位置，结合三角几何法计算出目标的实际角度 α；采用Fourier 拟合实现对目标直线运动测量结果偏差的优化。具体流程如图4 所示。

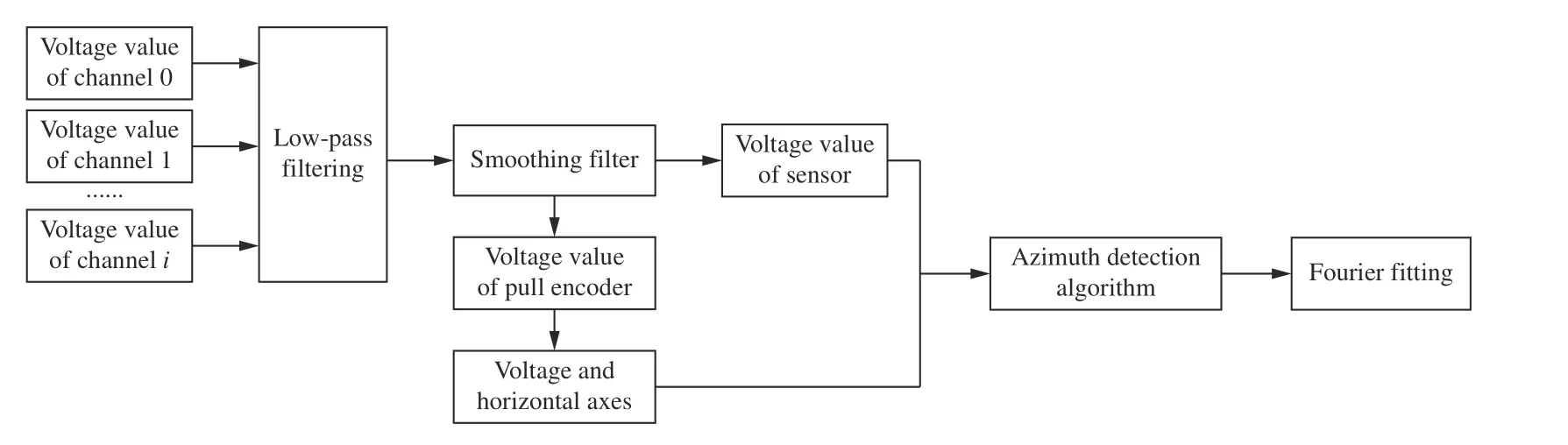
图 4 信号处理流程Fig. 4 Flow chart of signal processing

3 实验结果与分析

3.1 目标运动方位角检测结果与优化

图5（a）所示为目标距离传感器距离D=255 mm、v=30 mm/s 时连续采集的不同时刻的目标序列信号 Sn(t)（其中子传感器数量n=60，每一时刻信号曲线 Sn由传感器阵列中60 个子传感器信号组成，图5（a）中不同颜色曲线表示在不同时刻传感器阵列检测的目标信号 Sn(t)）及根据采集的序列目标信号计算的测量角度，如图5（b）所示。

目标在直线运动过程中，与传感器的相对距离发生改变。随着目标运动，传感器检测的目标信号 S 相位与强度幅值均发生改变。因此，根据 ∆S计算目标测量角度与实际角度存在的偏差。目标以v=30 mm/s，与距离传感器中心不同垂直距离D（D=255 mm、275 mm、325 mm、375 mm）作直线运动。不同距离下，根据目标直线运动采集的信号作算法处理获得测量角度，拉线编码器记录目标实际角度。测量角度与测量偏差数据拟合曲线如图6所示，经数据拟合统计分析，不同距离偏差值与测量角度存在一致变化关系。

图 5 序列信号及测量角度图Fig. 5 Schematic diagram of sequence signal and measurement angle

图 6 测量偏差与测量角度关系拟合图Fig. 6 Fitting chart of relationship between measurement deviation and measured angle

分析运动目标在不同距离D 下的角度偏差ε在测量角度范围内的偏差特征函数 F(δ,ε)，以实现目标方位角检测的标定。建立图3（b）所示视觉系统，结合三角视差原理，从而实现在2D 平面内对运动目标的快速测距定位。在传感器有效视角范围内，利用图3（b）实验装置进行多次实验，对目标检测角度作数据分析，发现不同距离下目标检测角度偏差存在一致变化关系，对角度偏差数据进行数据拟合分析，如多项式拟合、高斯拟合、傅里叶拟合等，分析得出在不同距离D 时，目标检测角度偏差 ε均符合一阶傅里叶拟合方程：

则目标水平运动实际角度表示为

获得适用于不同距离下目标方位角偏差函数后，使用计入偏差函数的方位角检测模型计算目标角度，与拉线编码器记录的实际角度作对比，验证模型适用性。不同距离测量角度、计入偏差测量角度与拉线编码器记录的实际角度对比如图7 所示。

对采集信号作算法处理获得测量角度，通过偏差拟合函数计算得到各测量角度对应的偏差，计入偏差后的测量角度即为目标角度。由图7 可以清楚看出，计入偏差的测量角度与拉线编码器记录的目标实际角度基本一致，表示该偏差拟合函数可用于目标检测角度的优化。计入偏差的测量角度与拉线编码器记录的目标实际角度之差为测量误差，目标在不同距离水平匀速直线运动的角度测量精度分析如表1 所示。

图 7 不同距离测量角度与实际角度对比Fig. 7 Comparison diagram of measured angle and actual angle at different distances

表 1 测量误差数据统计分析Table 1 Statistical analysis of measurement error data

实验结果表明，在D=375 mm 范围内，目标方位的检测误差在±2°以内，平均92.01%的测量误差小于±1.5°。因此，本文提出的基于目标运动模式方位检测模型可以实现目标方位的快速确定，从而用于双目测距平台中对目标距离的测量，对前后两时刻信号连续处理的方法有效减少计算的数据量与计算时间以实现快速测距功能。但从测量误差的数据分析可知，随着目标距离D 的增大，目标信号减弱，且存在目标信号不稳定跳动，使得算法计算精度降低，角度测量误差增大。

3.2 基于视差原理的仿生复眼系统距离结果

在目标方位角测量的有效范围内进行测距实验，目标距离双目阵列中心距离为D（D=255 mm、275 mm、325 mm、375 mm），双目基线距离为250 mm，以v=30 mm/s 作直线运动，根据方位确定算法获得各个阵列对目标的测量角度，拉线编码器记录目标的实际角度。通过三角测距原理计算测量距离，根据拉线编码器记录的目标x，y 位置参数获得目标的实际距离，两者的差值为测量误差。实际距离与测量距离对比如图8（a）所示，测量误差如图8（b）所示。

对测距结果以及测距误差数据统计分析得：D=255 mm 时，测量误差在−9.740 mm～7.711 mm 之间，其中100%的测量误差小于±10 mm；D=275 mm时，测量误差在−9.807 mm～9.242 mm 之间，其中100%的测量误差小于±10 mm；D=325 mm 时，测量误差在−7.753 mm～11.326 mm 之间，其中95.92%的测量误差小于±10 mm；D=375 mm 时，测量误差在−4.143 mm～13.906 mm 之间，其中93.88%的测量误差小于±10 mm。实验结果表明，在实现方位角度测量的基础上，利用双目测距原理可以实现运动目标的实时定位。但从误差数据统计分析可知，随着目标距离D 的增大，目标信号减弱、目标信号不稳定跳动，使得算法计算精度降低，角度测量误差增大，从而使测距误差增大。

图 8 双目测距结果及精度分析Fig. 8 Analysis of binocular ranging results and ranging accuracy

本文提出的目标方位检测法及测距算法对前后两时刻目标信号差值作定位算法计算，而传统测距算法对每一时刻信号均作定位算法计算。因此，本文算法的计算数据量比传统算法减少了一半。传统基于图像处理的测距算法在相同实验环境下，采集目标运动图像，对每一组图片进行特征匹配处理，如sift 算法，分别对左右眼图像进行特征点提取后作双目特征匹配，计算数据量大，算法运行时间在5 s 左右，算法计算时间长；针对本文传感器模型中的同一组目标信号，寻峰算法对采集的每组目标信号作定位算法，运算时间在0.2 s左右，方位角测量误差在4°左右，运行速度快但定位精度较低；在寻峰算法基础上提出的高斯拟合算法对采集的每组目标信号作定位算法，运算时间在1s 左右，方位角测量误差在0.6°左右，精度较高但是算法计算量大且运行速度较慢；本文提出的测距算法同时处理两组数据以实现目标测距，算法运算时间在0.4 s 左右，方位角测量误差在1.5°左右，检测精度高于寻峰算法，检测速度高于高斯拟合算法。与传统测距算法对运动目标每一时刻进行静态测距本质不同的是，本文提出的双目测距算法结合了运动的连续性，对前后两时刻目标信号作算法处理以实现运动目标的连续动态测距，减少了大量复杂的传统静态测距算法计算量，算法简单快速，连续性强，实时性较高，可应用于目标运动速度较快、需要实时快速检测运动目标且精度要求不高的场合。

4 结论

基于光电二极管研制的仿复眼多通道视觉传感器，本文提出的目标定位测距算法实现了在双目传感器阵列视野大重叠区域300 mm×375 mm 范围内目标距离的实时测量，测量误差在−9.807 mm～13.906 mm 范围内，其中平均97.45%的测量误差小于±10 mm。本文算法在数据处理上具有连续性，避免了传统双目测距算法对每一时刻目标信息作处理导致的计算量大、实时性低的缺点；且测距算法简单快速，可以有效减少智能移动机器人信息处理模块的复杂性，适用于需要快速确定目标位置的场合。但要提高传感器阵列对目标方位确定及距离测量的精度，需要提高信号采集系统的抗噪能力，在目前信号采集系统中添加合适的抗噪抑制模块，减少跳变信号，提高信号采集的稳定性，从而提高目标方位计算的准确度以实现智能视觉机器人对目标实时准确的定位测距功能。