一种群稀疏限制的消除条带噪声变分模型

陈 柳, 陈明举,2*, 吴 浩, 薛智爽

(1.四川轻化工大学 人工智能四川省重点实验室，四川 自贡643000；2.西南科技大学 特殊环境机器人技术四川省重点实验室, 四川 绵阳 621000)

1 引 言

由于平面阵列中不同探测单元本身的差异以及外界的电磁与温度等因素的影响，导致不同探测单元具有不同的响应函数，此外平面阵列在正反来回扫描中存在行间差异，因而使获得的图像出现与扫描方向相同的条带噪声[1-2]。条带噪声广泛存在于红外图像与光谱遥感图像中，造成图像视觉质量的下降，不利于对图像进行分析、识别等后续处理。因此，采用有效的方法去除条带噪声，提高图像的清晰度是图像处理中一个热门课题。

目前，条带噪声去除主要分为频域滤波方法和空域统计特征方法。频域滤波方法主要利用条带噪声具有周期性的特点，通过频谱分析确定条带噪声所处频域区域以实现噪声的消除[3-4]。由于图像部分信息与条带噪声处于同一个频段，频域法在去除噪声的同时不可避免地会消除部分图像信息，从而导致去噪后图像细节模糊与阶梯效应。基于图像空域统计特征方法主要有匹配法、稀疏分解和变分法等方法。匹配法以图像像素值的统计特性为前提，去噪效果依赖于统计的准确性，当图像像素较少或像素值不均匀分布时，其去噪性能变差[4-5]。稀疏表示(Sparse decomposition，SD)利用图像空间上的冗余性与相似性，利用字典学习与稀疏系数重构图像，实现图像与噪声的分离[6]。Zhang等人[7]认为原始图像可以表示成低秩矩阵，提出了去除条带噪声的图像的低秩稀疏模型(Low-rank single-image decomposition，LRSID)，有效地实现了遥感图像的复原。Dou等人[8]根据图像相邻像素值的相关性与条带噪声的特性，构建非凸的L0范数稀疏模型，并通过实验证明该模型具有较好的去噪性能。稀疏表示可以有效地重构图像，但未考虑条带噪声的特性，其去除条带噪声的性能存在一定的局限。鉴于此，Bouali等人[9]依据条带噪声的特点，将变分理论(Total variational，TV)应用到条带噪声去除中，构造了去除条带噪声的L1范数单向变分模型(Unidirectional total variational，UTV)。该模型在消除条带噪声的同时能较好地保护图像的细节信息，但该模型过度对图像梯度约束，不可避免地产生阶梯效应。随后，一些学者对UTV模型进行改变，提出了一些改进模型。如，Chang等[10]将图像的framelet变换系数的L1范数加入UTV模型的限制项，实现了条带噪声区域与非噪声区域不同平滑。Ayoub等[11]针对UTV模型过度平滑图像的边缘问题，将边缘感知权值引入到UTV模型，更好地保护了图像的边缘信息。然而，这些变分模型着重变分技术对图像梯度的约束[12-13]，未充分考虑图像空域的相似性与条带噪声的几何特性，去噪性能有待进一步提高。

鉴于此，本文针对条带噪声的特性，在单向变分模型的基础上，采用群稀疏技术对条带噪声加以限制，提出充分考虑图像结构相似性与条带噪声几何特性的群稀疏技术约束的单向变分模型(Unidirectional total variation model with group sparsity constraint，UTVGSC)，并给出该模型的优化求解过程。

2 群稀疏约束的单向变分模型

2.1 单向变分模型的不足

假设图像u受条带噪声s的干扰，获得退化图像f可以表示为：

f=u+s，

(1)

与常见的随机噪声不同，条带噪声s是一种结构性强的噪声，具有单一方向的结构特性，在该方向的梯度近似不变, 如图1(b)所示。受条带噪声干扰的图像，通常只有一个方向的梯度受条带噪声的影响，另外一个与之正交方向的图像梯度几乎不受干扰，条带噪声干扰图像如图1(c)所示。

图1 条带噪声与含噪图像Fig.1 Stripe noise and noisy images

经典的去除条带噪声的单向变分模型就是基于上述特性构建的，通过极小化图像x方向(水平方向)的梯度与条带噪声y方向(垂直方向)的梯度的L1范数，建立的模型如下：

(2)

由于条带噪声在y方向梯度几乎为0，对‖ys‖1极小化可以减少条带噪声；图像在x方向的梯度连续，极小化‖xu‖1项可以有效地消除高频噪声对图像的影响。该单向变分模型在去除图像条带噪声中取得了一定的效果，但该模型过度强调变分模型对图像的描述，不可避免地在图像的平滑区域产生阶梯效应。同时，该模型忽略条带噪声结构上的相似性，未充分利用条带噪声之间存在的稀疏性，去除条带噪声的能力有待进一步提高。

2.2 群稀疏约束的单向变分模型

图像的群稀疏表示在实现图像整体稀疏表示前提下，更好地考虑图像中的结构相似信息。图像群稀疏表示通过极小化图像的L1,2范数来实现。令A=[α1,…,αl]∈Rk×l，αi为矩阵A的一列，采用L1,2范数对矩阵A加以限制：

(3)

通过极小化‖A‖1,2便可以实现矩阵A的群稀疏表示。相对于稀疏表示，群稀疏表示不仅使矩阵每一列不为0的系数尽量少，且各列不为0的系数出现的位置相同(图2(b))，从而在实现图像稀疏表示的前提下，有效地表达图像中相似结构信息。

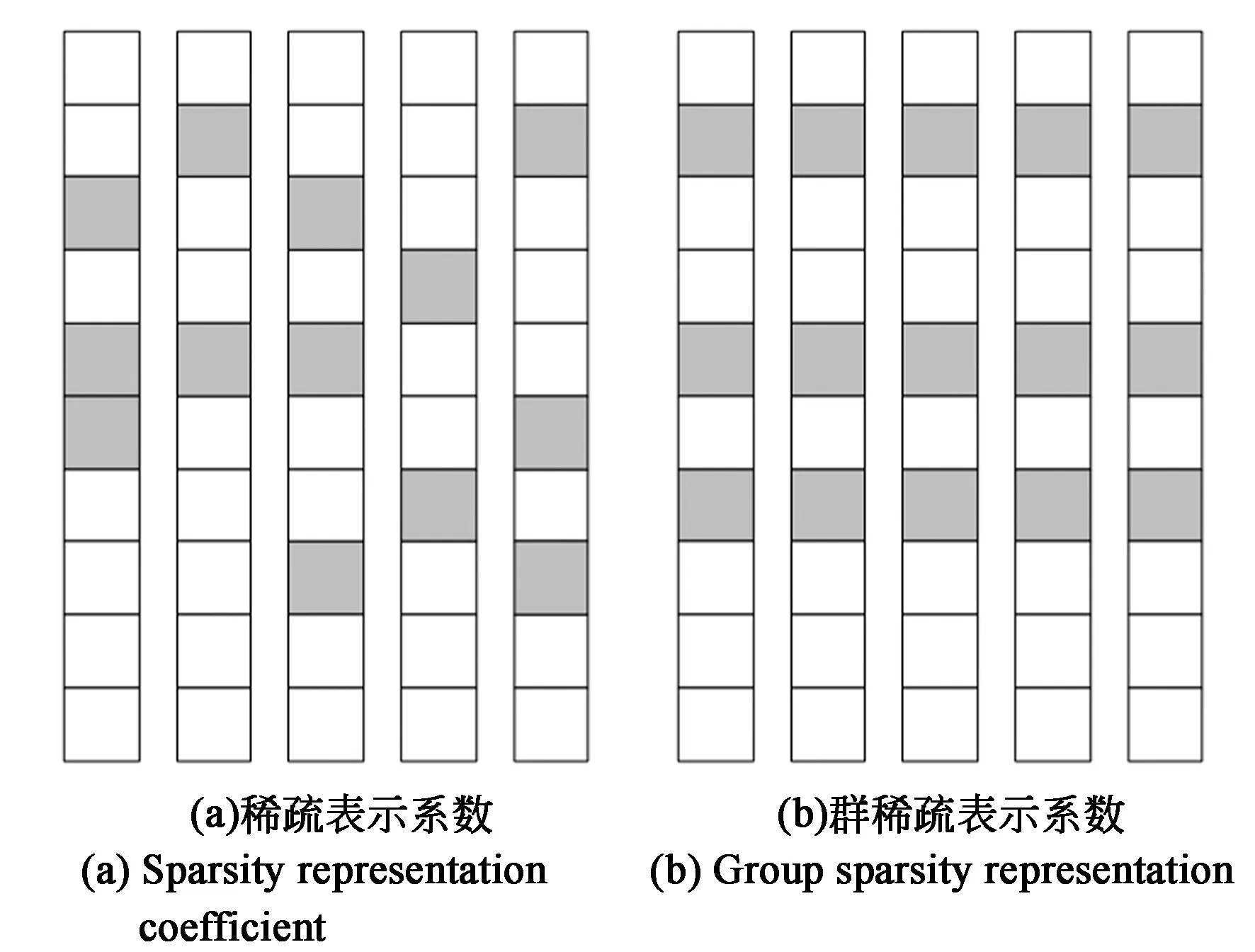
图2 稀疏表示与群稀疏的系数比较(图中黑色方块表示非0系数)Fig.2 Comparison between sparsity and group sparsity(the black squares are nonzero coefficients)

考虑到条带噪声之间存在极强的结构相似性，采用群稀疏技术能有效实现对条带噪声的描述。为有效利用条带噪声之间存在的结构相似性，本文将对条带噪声加以群稀疏限制引入到单向变分模型中，以减弱单向变分模型产生的阶梯效应，更好地消除条带噪声，建立群稀疏技术约束的单向变分模型(Unidirectional total variation model with group sparsity constraint, UTVGSC)：

(4)

式(4)中:‖s‖2，1对条带噪声采用群稀疏表示，使优化求得的图像u更接近原始真实图像。

2.3 群稀疏约束的单向变分模型的优化求解

式(4)建立的UTVGSC模型是一个凸函数，可采用经典的交替方向乘法(Alternating direction method of multipliers，ADMM)对其优化求解[14]。引入辅助变量v、z与w，模型(4)非限制性问题可以转化为带限制项的极小化问题：

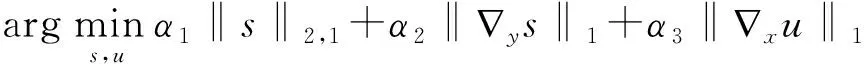
(5)

式(5)表示成拉格朗日函数为：

(6)

其中Λ为拉格朗日乘子。采用交替方向最小化的思想，式(6)可以分解成v,z,w,s,Λ几个子问题。

v子问题可以表示为：

(7)

令v=[v1,...,vl]，vi为矩阵v的第i列，式(7)可以转化为[15]：

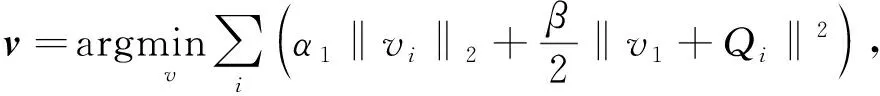
(8)

v的求解可以通过阈值收缩迭代求得：

(9)

z、w子问题可表示为：

(10)

(11)

z、w的值可以通过软阈值迭代更新求得：

(12)

(13)

s子问题可以表示为：

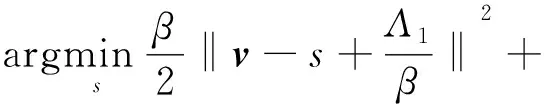
(14)

式(14)极小化求解问题，可令其导数为0，得：

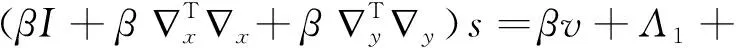
(15)

s可以通过以下闭式解求得：

(16)

式(16)中F与F-1分别为傅里叶正反变化，其中，

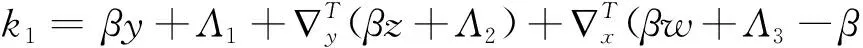
为确保迭代过程的收敛性，迭代中产生的s(t)如果小于0，将其变成0；如果s(t)大于图像像素值的最大值，则将其变成像素最大值。

另外，拉格朗日乘子Λ=[Λ1,Λ2,Λ3]的更新公式为

(17)

综上所述，群稀疏约束的单向变分模型的ADMM优化求解可以简化如下：

群稀疏约束的单向变分模型的ADMM优化求解步骤Input: 含条带噪声图像fInitialize:u0=f,s0=f-u0While “Not converged” do:按式(9)更新v按式(12)、(13)更新z,w按式(16)更新s按式(17)更新拉格朗日乘子Λend whileOutput: 条带噪声s,从而得到u=f-s.

3 试验结果及分析

为证明本文群稀疏约束的单向变分模型去除条带噪声的性能，将本文UTVGSC模型与LRSID、TV、DTV、SD去噪模型进行对比分析。实验中分别选取红外图像与高光谱遥感图像两组图像加入不同强度的条带噪声进行对比分析，采用峰值信噪比(Peak Signal to Noise Ratio，PSNR)[16]和结构相似性(Structral Similarity Index，SSIM)[17-18]作为客观评价指标。

3.1 红外图像条带噪声的消除实验

红外图像选取具有代表性的“Elephant”、“Warcraft”、“Tank”、“Man” 4幅图像加入条带噪声进行实验，原始图像如图3所示。表1给出不同模型去除条带噪声前后的PSNR与SSIM的值，从表1可以看出本文的UTVGSC模型的PSNR与SSIM均高于其余4种模型。

图3 原始红外图像Fig.3 Original infrared images

表1 不同红外图片不同模型去除条带噪声结果Tab.1 Denoising results of different models for different infrared images

续 表

图4给出4幅红外图像采用不同模型去噪后的结果。从图中可以看出，稀疏分解的结果残留大量的条带噪声，这是由于条带噪声和图像一样具有稀疏性，单一的稀疏变换无法将二者分离。TV去噪的结果仍然存在较强的条带干扰，这是由于TV模型未考虑条带噪声的方向性，从而不能有效去除条带噪声。与TV模型相比，DTV更好地考虑到条带噪声的方向性，去除图像条带噪声的性能有一定幅度的提高，条带噪声在一定程度上得到减弱，如图4(d)所示。LRSID较好地实现了图像与条带噪声的分离，但去噪后图像仍然存在少许条带噪声阴影。在所有的模型中，本文提出的UTVGSC模型获得图像是最清晰的，几乎未发现残留的条带噪声，图像的轮廓与细节都得到了较好的保留，去除条带噪声的性能最优。

(a)噪声图(a) Noise images

(b)SD结果(b) SD results

(c)TV结果(c) TV results

(d)DTV结果(d) DTV results

(e)LRSID结果(e) LRSID results

(f)本文UTVGSC结果(f) UTVGSC results图4 红外图像不同模型处理结果Fig.4 Infrared images before and after restoration

3.2 高光谱图像条带噪声的消除

图5 原始高光谱图像Fig.5 Original hyperspectral images

高光谱遥感图像同样选取具有代表性的4幅图像加入条带噪声进行实验，原始高光谱遥感图像如图5所示。表2给出不同模型的PSNR与SSIM的值。表2数据再次证明，本文UTVGSC模型去除条带噪声的峰值信噪比与结构相似性都明显高于其他模型。通过对比图6中各图，再一次证明UTVGSC模型去除条带噪声获得的图像清晰度最高，去噪性能最优。

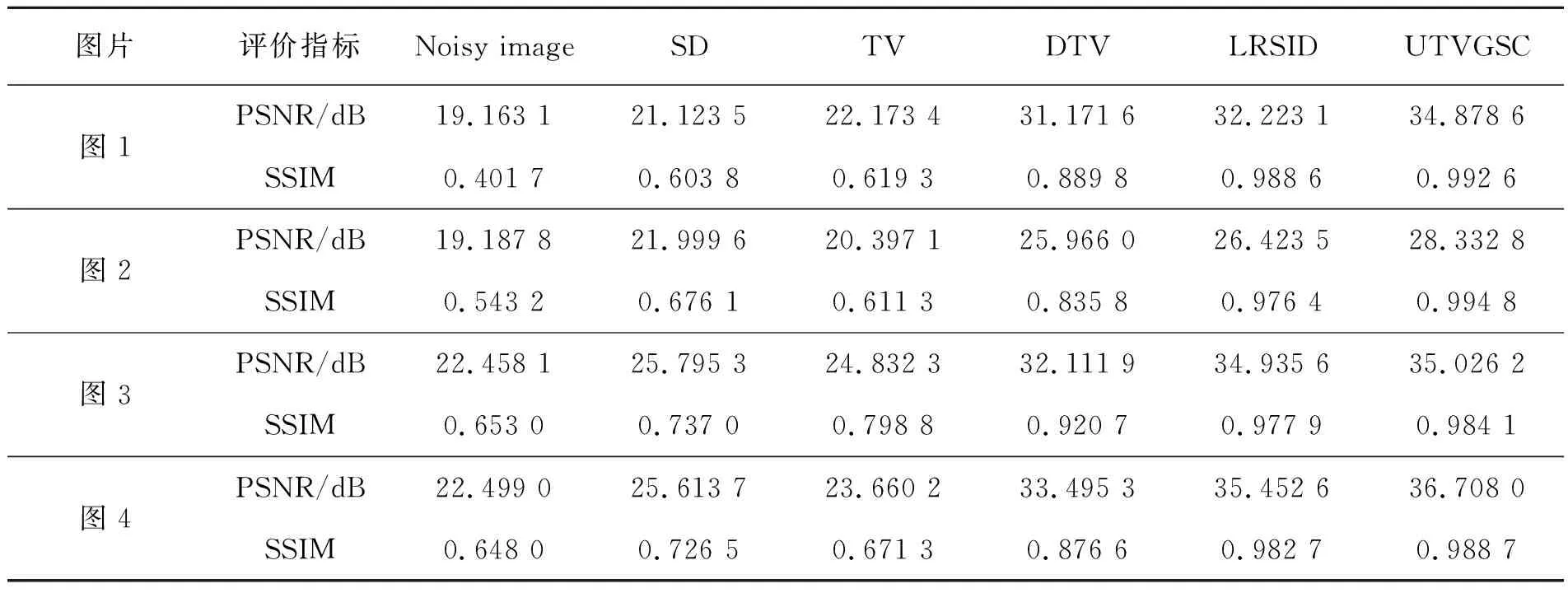
表2 不同高光谱遥感图片不同模型去除条带噪声结果Tab.2 Denoising results with different models use different hyperspectral images

(a)噪声图(a) Noise images

(b)SD结果(b) SD results

(c)TV结果(c) TV results

(d)DTV结果(d) DTV results

(e)LRSID结果(e) LRSID results

(f)本文UTVGSC结果(f) UTVGSC results图6 高光谱遥感不同模型处理结果Fig.6 Hyperspectral images before and after restoration

4 结 论

针对现有的变分模型未充分考虑条带噪声结构之间存在相似性的缺点，本文将群稀疏技术引入到单向变分模型中，建立群稀疏限制的单向变分模型，并推导出该模型的交替迭代优化求解过程。由于本文提出的群稀疏技术限制的单向变分模型在极小化图像变分项的前提下，利用群稀疏技术能充分考虑条带噪声的结构相似特性，因此较好地实现了条带噪声的估计，在有效去除图像条带噪声的同时能更好地保留图像的结构细节信息。在对比实验中，从主客观两个方面证明本文提出的群稀疏限制的单向变分模型具有更好的去除条带噪声性能。因此，本文提出的群稀疏限制的单向变分模型能有效去除红外、高光谱图像中的条带噪声，具有极大的学术价值与广泛的应用前景。