基于流固共轭传热的两相流动数值模拟及燃料子通道CHF预测研究

冯琳娜，李 权,*，黄永忠，刘振海，齐飞鹏，M. Avramova

(1.中国核动力研究设计院 核反应堆系统设计技术重点实验室，四川 成都 610213；2.北卡罗来纳州立大学，美国 罗利 27695)

对于压水堆燃料组件设计，临界热流密度(CHF)是评价其热工水力性能的重要参数之一，一旦燃料棒的热流密度超过CHF，就有可能发生燃料棒烧毁，进而导致放射性物质释放的风险。因此，对于燃料组件设计，需掌握其CHF值[1]。目前CHF值主要通过试验的方法获取，但试验成本高、周期长，研究者一直在寻找替代试验的数值预测方法。

对CHF预测的研究由来已久，如经验关系式、理论模型(汽泡雍塞模型等)、CHF查询表等，但经验关系式由试验数据拟合得到，只适用于特定的燃料组件，对于新的燃料组件设计则无法适用；理论模型、CHF查询表等用于燃料组件复杂结构则需引入一些修正因子，无法准确评估燃料组件细节特征的影响[2]。因此随着近年来CFD技术的兴起，研究者一直在尝试采用两相CFD方法进行CHF预测。Vyskocil等[3]利用NEPTUNE_CFD程序，采用两相CFD分析的方法，认为空泡份额超过0.8时CHF发生，并对竖直加热的圆管CHF值进行了预测。李权等[4-5]采用沸腾曲线的方法，对均匀加热圆管和非均匀加热圆管的CHF值进行了预测，并探究了不同工况的影响。李松蔚等[6]采用不考虑相间质量传递的两相CFD分析的方法，分析了带7个格架的5×5棒束通道两相流动特性，并通过格架下游的空泡份额分布定性地判断CHF特性。但上述数值模拟都只针对流体区域进行求解，热工边界较为简单，未能考虑流固共轭传热引起的轴向非均匀传热特性的影响，也无法准确捕捉CHF发生时固体表面的温度变化。而陈广亮等[7]的研究表明，采用流固共轭传热可更加准确地预测周向的非均匀传热特性。

因此，本文基于流固共轭传热和两相CFD分析的方法，建立相应的数值模型，实现流固共轭传热和过冷沸腾两相流动的耦合求解，并在此基础上建立燃料子通道CHF的数值预测方法。

1 数值模型

1.1 固体导热模型

采用稳态计算，固体导热方程如下：

(1)

(2)

式中：λs为固体的热导率；Ts为固体温度；Qv为体热源。

1.2 流固共轭传热数值模型

流固共轭传热主要通过流体和固体的交界面进行传递，交界面上固体和流体的温度、热流密度保持连续。

Ts|surface=Tl|surface

(3)

qs|surface=ql|surface

(4)

式中：Ts|surface和Tl|surface分别为交界面上固体和流体的温度；qs|surface和ql|surface分别为交界面上固体域和流体域的热流密度。

1.3 过冷沸腾两相流动数值模拟

对过冷沸腾两相流动的CFD模拟，以欧拉两流体模型为框架，结合壁面沸腾模型进行。

1) 欧拉两流体模型

欧拉两流体模型是将每一相均看成充满整个流动空间的连续介质，用空泡份额来表征每相所占据的体积份额，对两相分别建立质量、动量和能量守恒方程，通过两相间的界面传递模型使方程组封闭。建立的守恒方程为：

(5)

(6)

(7)

2) 两相间的动量传递

两相间的动量传递主要通过界面力实现，本文主要考虑曳力和湍流耗散力。

Mk=FD,k+FTD,k

(8)

式中，FD,k、FTD,k分别为由曳力、湍流耗散力引起的两相间的动量传递。

曳力FD通常包含两部分：时均值和脉动值。时均部分的曳力计算关系式为：

(9)

式中：ur=ul-ug为两相间的相对速度；CD为曳力系数，一般由Tomiyama关系式[8]计算；指数n取4，用于考虑高空泡份额的效应，也称汽泡云集效应[9]。

曳力的脉动部分，也称为湍流耗散力，表征由液相湍流引起的动量传递。其值由下式计算：

(10)

3) 汽泡直径分布

汽泡脱离壁面进入主流区后，会与主流区的液体进行热交换，汽泡直径会发生变化。由于汽泡在主流区主要发生冷凝，因此通常汽泡直径为主流液体过冷度的线性关系式：

(11)

式中：dB为汽泡在主流区的直径分布；Tsub为液体的过冷度。本文参考文献[10]，取Tsub,1=13.5 K，dB1=0.1 mm；Tsub,2=5 K，dB2=2 mm。

4) 壁面沸腾模型

对过冷沸腾的模拟，还需加热壁面的源项。为考虑高空泡份额及临界热流密度的影响，本文采用拓展后的壁面沸腾模型，将壁面热流密度分成4部分，机理示意图如图1所示。

图1 热流密度分配示意图[7]Fig.1 Diagram of heat flux distribution[7]

(12)

式中，qw=qs|surface为加热壁面的热流密度；qc、qq、qe、qg分别为液体单相对流传热、激冷对流传热、汽化潜热及气体单相对流传热部分的热流密度，其详细表达式参见文献[9]；Kdry为壁面烧干面积比，由式(13)计算。

(13)

(14)

式中：αdry为临界空泡份额；αδ为近壁面空泡份额。本文参考Weisman & Pei的汽泡雍塞理论[11]，αdry取值为0.82，αδ则取距壁面最近的网格栅元的值。

式(13)中各项的表达式参见文献[5]，与文献[5]不同的是，本文活化核心密度由Lemmert-Chawla模型[12]计算：

(15)

式中：C=210；m=1.805；Ts,sup=Ts-Tsat为加热壁面的过热度，Tsat为液体饱和温度。

汽泡脱离直径由Tolubinsky模型[13]计算：

Dd=d0exp(-Tsub/45)

(16)

式中：Dd为汽泡脱离直径；d0为参考直径。本文主要模拟高压工况，高压下汽泡脱离直径更小，因此参考Krepper等[10]的研究取d0=0.6 mm。

上述数值模型均应用于软件STAR-CCM+9.04[14]。

2 燃料棒典型栅元共轭传热两相流动分析

2.1 数值模型建立

沸水堆中冷却剂处于沸腾两相流动状态，可为本文建立的数值模型提供验证。选择典型的BWR6沸水堆燃料棒[14]，该燃料棒长度为3.7 m，燃料芯块直径为10.68 mm，燃料芯块的功率密度为226.4 MW/m3，包壳壁厚为0.81 mm，冷却剂运行压力为7.17 MPa，本文取该燃料棒前1 m进行模拟，该阶段处于过冷沸腾两相流动状态。详细的几何模型如图2所示。

图2 几何模型及网格示意图Fig.2 Diagram of geometrical model and mesh

在数值模拟中，采用二维旋转对称模型，对该几何模型进行建模。在燃料芯块与包壳之间，通过增加热阻的方式来模拟燃料棒中预填充氦气的影响。

采用结构化网格进行网格划分，经过网格敏感性分析，确定总的网格数量为13 600，局部网格示意图如图2所示。

2.2 模型验证

基于上述网格和所建立的数值模型，进行燃料芯块、包壳、冷却剂的共轭传热两相模拟，计算得到靠近出口处的芯块温度、包壳温度和冷却剂温度沿径向的分布与理论值[14]的对比如图3所示。从图3可见，数值模拟得到的芯块温度、包壳温度和流体温度均与理论值符合良好，验证了本文基于流固共轭传热的过冷沸腾两相流动数值模型和分析方法的正确性。

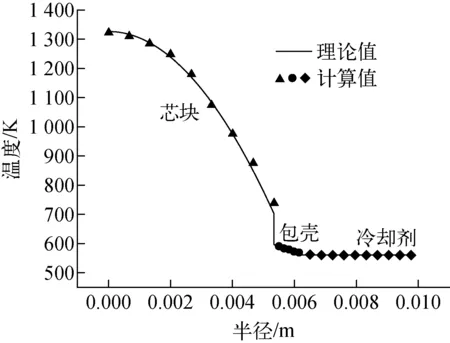
图3 芯块、包壳及冷却剂温度沿径向的变化Fig.3 Radial temperature distribution of fuel pellet, cladding and coolant

3 典型燃料子通道内两相流动及CHF数值预测

3.1 几何建模及网格划分

在典型栅元的基础上，探索燃料子通道内两相流动和CHF的预测方法，以国际性基准验证实验PSBT[15]中子通道S1的试验数据进行模拟。子通道S1包含4块1/4加热片，其栅元距离为12.6 mm，结构示意图如图4a所示，加热元件采用铬镍铁合金，直径为9.5 mm，在子通道外采用矾土进行绝缘。加热段长度均为1.555 m，为均匀加热。试验测量了加热段入口1.4 m处截面的平均空泡份额。

图4 子通道S1及网格划分尺寸示意图Fig.4 Schematic diagram of subchannel S1 and partial grids

由于几何模型的对称性，采用1/8子通道模型进行建模并施加对称边界条件，同时对加热元件和流体域进行建模。轴向上分别增加20 mm的入口段和出口段，以排除入口和出口效应的影响。采用结构化网格进行数值模拟，通过网格敏感性分析，最终选择的网格示意图如图4b所示。

3.2 两相流动数值模拟

基于上述网格和数值模型，对表1中14个工况进行数值模拟，计算得到距加热段1.4 m高度处的截面平均空泡份额计算值与试验值的对比如图5所示。从图5可见，计算值与试验值总体符合良好，表明本文模型可用于燃料子通道过冷沸腾两相流动模拟。

表1 子通道两相流动模拟工况Table 1 Test condition of boiling two-phase flow in subchannel

3.3 典型子通道CHF预测

在两相流动模拟的基础上，对CHF的预测进行研究。以1.2221工况为例，采用准瞬态的方法，保持入口条件不变，逐步增加加热功率，并监测加热元件的最大壁面温度，计算得到的最大壁面温度随热流密度(加热功率转换得到)的变化如图6所示。从图6可见，在进入到过冷沸腾区后，刚开始时，壁面最大温度随热流密度的提升变化幅度较小。但随着加热功率的提高，当达到一定的热流密度后，壁面温度升高的趋势明显增大，有温度飞升的趋势，此现象与临界热流密度试验中出现壁面温度飞升的现象非常近似，因此，本文将变化曲线中壁面温度出现飞升作为临界热流密度发生的判据。则对于1.2221工况，CHF预测值为2 400 kW/m2。

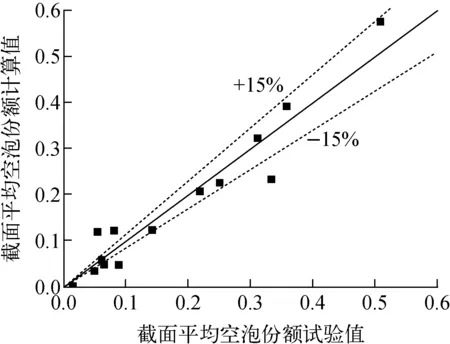
图5 两相流动模拟工况计算值与试验值的对比Fig.5 Comparison between calculated and test values of two-phase flow simulation

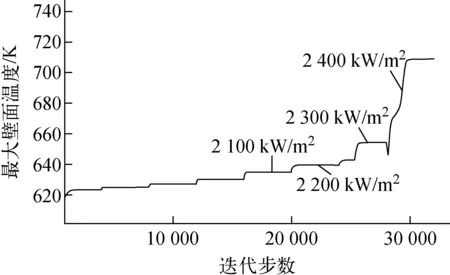
图6 1.2221工况的最大壁面温度随热流密度的变化Fig.6 Change of maximum wall temperature with heat flux in 1.2221 condition

在PSBT子通道实验中，并无测量相关的CHF实验数据。本文借助2006年的CHF查询表[16]，计算得到CHF的实验值。对于1.2221工况，CHF查询表值为2 088 kW/m2，预测误差为14.9%。造成CHF预测值较查询表值大的因素有两个：1) 热流密度为2 400 kW/m2时，出口的局部含汽率达0.075，根据文献[5]研究结果，在较高含汽率下，预测值容易较实验值高；2) 热流密度2 400 kW/m2时，壁面最大空泡份额已超过0.82，此时计算得到的局部含汽率较实际CHF值偏高，导致通过CHF查询表得到的CHF值偏低。

基于壁面温度飞升的方法，对表1中1.2221、1.1221、1.2211、1.2231、1.2233、1.2234、1.2423、1.2121、1.3221共9个工况的CHF值进行了预测，CHF预测值与查询表值的对比如图7所示。

图7 子通道CHF预测值与查询表值的对比Fig.7 Comparison of predicted CHF with look-up table data

由于上述两个因素，对于大部分工况，预测值均较CHF查询表值高，9个工况的平均预测误差为15%。但对于1.2423和1.3221工况，预测值较CHF查询表值低。对于1.2423工况，流量为1 369.4 kg/(m2·s)，明显小于其他工况；而1.3221工况的压力为12.3 MPa，也小于其他工况；文献[5]发现，采用同一套数值模型对CHF进行预测，随着压力和流量的增加，预测值与实验值的比值逐渐增加，即在相对低压、低流量下，预测值较实验值低，因此导致这两个工况的预测值较实验值低。本文模拟的趋势与文献[5]相符合。

以上分析表明，基于流固共轭传热两相流动模拟构建的CHF预测方法，可适用于子通道内CHF的数值预测，但本文CHF实验值的获取方式仍需进一步提高，以更加准确地评估本文预测方法的精度。

4 结论

本文基于流固共轭传热和两相CFD分析的方法，建立了考虑共轭传热的过冷沸腾两相流动数值模型，并通过典型沸水堆燃料棒的分析，验证了数值模型的正确性。在此基础上，对燃料子通道的两相流动进行了模拟，并采用准稳态求解的方法，基于加热壁面温度飞升，建立了CHF预测方法。采用该方法，对不同工况燃料棒束子通道内的CHF进行数值模拟，验证了CHF预测方法的正确性。本文基于共轭传热两相流动的CHF预测方法可为后续燃料组件和格架等部件的设计优化提供参考。