基于混合核函数支持向量机的风电机组发电机温度预警方法

曹力，潘巧波，王明宇，马东

（华电电力科学研究院有限公司，杭州310030）

0 引言

近年来，风电事业得到了长足的发展，但风电机组长期工作在恶劣环境中，其中齿轮箱、发电机、叶轮等大部件的工作状态直接影响整机的运行性能［1-3］。因此采取有效的状态监测与故障诊断方法对关键部件进行分析研究，预警故障并尽早开展排查检修工作，对于风电机组的健康管理及能效提升有重要的指导意义。

发电机是风电机组工作的关键环节，承担着机械能转化为电能的功能，其工况比较复杂，发生故障后检修周期长、检修难度大，许多专家针对发电机状态监测与故障诊断开展了相应的研究。文献

［4］阐述了双馈发电机组机械类故障和电气类故障常用的信号分析技术。文献［5］使用改进粒子群优化-反向传播（IPSO-BP）算法建立齿轮箱正常工作状态下的温度模型并用于故障预测，通过残差分析实现预警。文献［6］将极端梯度提升（XGBoost）模型与其他4类回归预测模型分别进行齿轮箱温度预测模型试验，结果表明XGBoost 模型在齿轮箱温度预测中综合性能要优于其他4 类模型。文献［7］提出一种堆叠自编码网络深度方法，使用自适应阈值监测重构误差的趋势变化，实现对故障的判定。上述文献在研究时或用信号分析手段，或用机器学习算法，从机理角度及数据角度对风电机组齿轮箱、发电机工作状态进行了分析，均取得了一定的研究成果，但都存在建模学习难度大，状态劣化时间点定位不准确的问题［8-10］。

支持向量机（SVM）是一类按监督学习方式对数据进行二元分类的广义线性分类器。它易于建模，对于风电机组数据采集与监视控制（SCADA）系统的数据有良好的适应性，核函数支持向量机（KSVM）常用的有2 类核函数:多项式核函数（Polynomial Kernel）和 高 斯 核 函 数（Gaussian Kernel）［11-13］。高斯核函数可以把特征映射到无限多维，计算比较简单；但是高斯核函数存在计算速度慢，容易过拟合的缺点［14-15］。多项式核函数泛化能力强，但是学习能力较弱。故可以将2 种核函数结合起来，发挥各自的优点。

本文提出一种基于混合核函数支持向量机（HK-SVM）的方法来对风电机组发电机温度进行建模，计算理想值和实际值的差值，通过历史良好的样本数据确定监测指标阈值，再实时通过滑动窗口计算有关指标，完成预警工作。

1 风电机组信息

本文研究对象为河北某风电场#134 和#74 机组，型号均为华锐SL1500/82，额定功率为1 500 kW，额定风速为10.5 m/s。

选取#134机组2018年10月10日至2019年3月2 日共178 865 条数数据及#74 机组2018 年8 月10日至2019年3月2日共248 125条数据进行研究，采集频率均为1 min/次。2 台机组故障检修记录见表1。

表1 2台机组故障检修记录Tab.1 Troubleshooting records of the two units

2 基于混合核函数支持向量机原理

2.1 支持向量机原理

支持向量机通过寻找一个超平面将2类样本点切割开，可用于回归问题。给定训练数据集

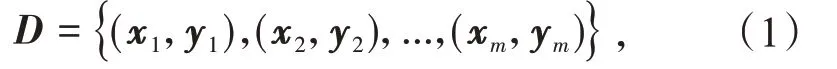
式中:xi和yi分别代表样本点的输入和输出，i=1，2，…，m。训练以期望得到一个回归模型f（x）=ωTx+b，使得f（x）与y的差值尽可能小，ω和b是表征超平面的参数。和传统模型计算输出f（x）与y的差值来衡量损失不同，支持向量回归（SVR）假设我们能允许f（x）与y之间最多存在ε的误差，当且仅当f（x）与y之间差的绝对值大于ε时才计算损失。SVR 问题可写作

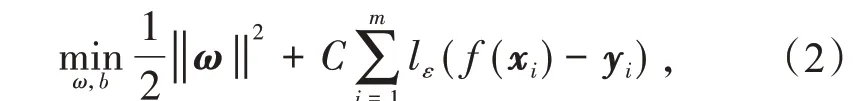
式中:C为正则化常数；lε表示损失函数，表达式为

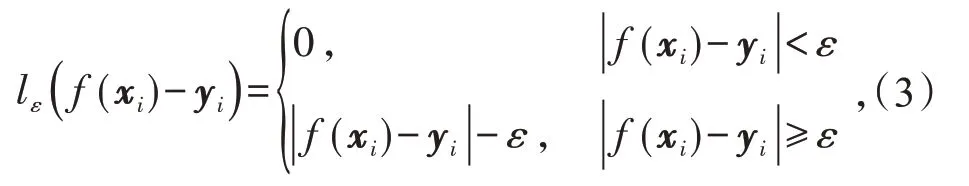
引入松弛变量ξi，，则式（2）变为

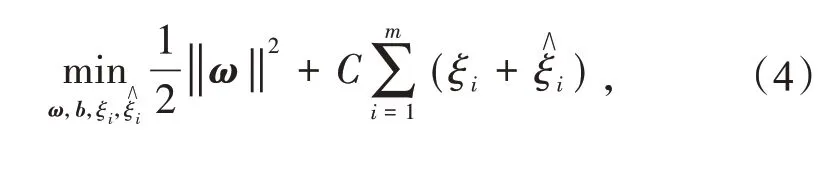
满足约束条件:

引入拉格朗日乘子:

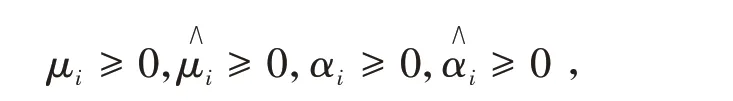
得到下面的拉格朗日函数:

令式（5）对ω，b，ξi，的偏导数为0，可得

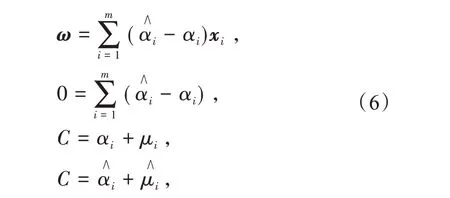
将式（6）代入式（5），得到SVR对偶问题:

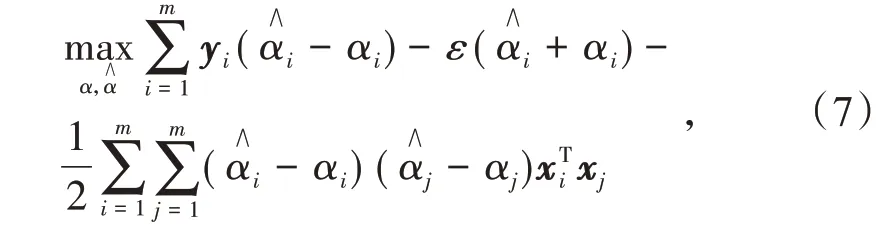
满足约束条件:

上述过程满足的库恩塔克条件（KKT）为

SVR解为

完成以上求解的一个基础是使用核函数将样本点映射到高纬度特征空间。传统向量机选用核函数要求必备一定的先验知识，否则只能凭借经验或者凑试法来选择误差最小的核函数。本研究使用多项式核函数、高斯核函数的混合核函数进行处理。表达式为

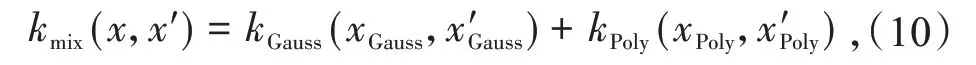
式中:kGauss为高斯核函数；xGauss为高斯核函数的输入值；x'Gauss为高斯核函数输入值的特定变换值；kPoly为多项式核函数；xPoly为多项式核函数的输入值；x'Poly为多项式核函数输入值的特定变换值。

选用混合核函数支持向量机进行发电机预警，流程如图1所示。

图1 发电机预警流程Fig.1 Flowchart of the generator warning system

2.2 混合核函数对回归性能的改进

2.2.1 输入参数的确定

回归问题需要确定输入量及输出量，本研究的输出量为发电机驱动端轴承温度。选取输入量时应考虑其对于输出量的影响程度。用相关系数r表征为

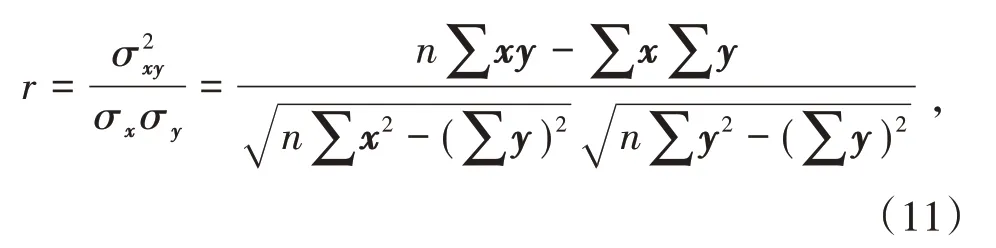
式中:x和y为2 个不同的样本集；σx和σy分别为x和y的标准差，σxy为x和y的协方差，n为样本容量。

分别计算#134 机组和#74 机组的SCADA 数据中42 个参数与发电机驱动端轴承温度两两相关的系数，选取部分参数的相关系数，见表2。

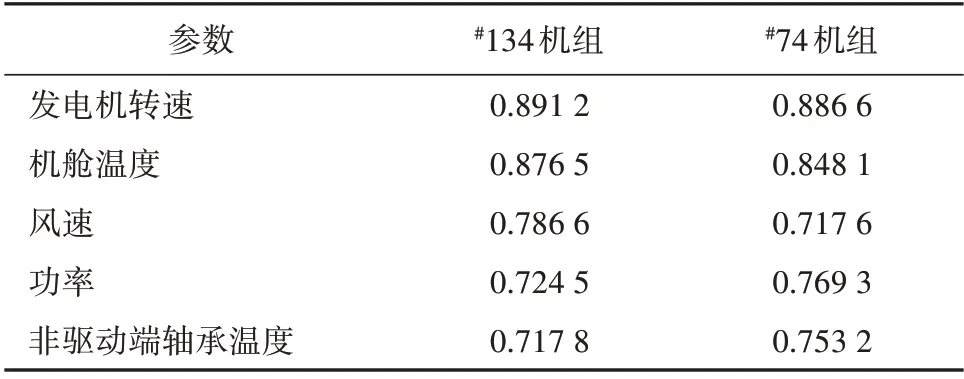
表2 发电机驱动端轴承温度与部分参数的相关系数Tab.2 Correlation coefficient of the generator bearingtemperature at driving end and some parameters

考虑冗余性能，最终确定输入参数为发电机转速、机舱温度、风速、非驱动端轴承温度。

2.2.2 各类核函数支持向量机训练

选用#134 机 组2018 年10 月10 日至11 月10 日共35 848 条数据及#74 机组2018 年8 月5 日至10 月10 日共71 893 条数据进行支持向量机回归训练。分别选用高斯核函数、多项式核函数、混合核函数来进行训练。需要说明的是，原始数据在训练时需要经过去除异常值（如超正常范围点、零点值等）的处理；同时，考虑到不同参数之间量纲不同，取值范围存在较大差异，整个训练分析过程中均对所有数据进行归一化处理，确保建模的有效性。

训练过程中采用KFold 函数交叉验证，将原始数据分成k组，将每个子集数据分别做一次验证集，其余的k-1组子集数据作为训练集，这样会得到k个模型。这k个模型分别在验证集中评估，结果用泛化误差表示。将泛化误差加权平均得到交叉验证误差，然后使用泛化误差和交叉验证误差计算每个模型的平均泛化误差，选择平均泛化误差最小的模型作为结果模型。

最后，使用若干指标评定不同核函数的训练效果，见表3。表3中，R2为决定系数，值越接近1，说明模型拟合效果越好；RMSE 为均方根误差，值越小说明拟合值和实际值越接近。

表3 几类核函数支持向量机训练效果Tab.3 Training performance of support vector machines using various kernel functions

训练结果说明如下:

（1）使用混合核函数的支持向量机的R2及RMSE 指标接近于使用高斯核函数的支持向量机，两者均优于使用多项式核函数的支持向量机；

（2）使用多项式核函数的支持向量机训练时间与使用高斯核函数的支持向量机接近，均短于使用混合核函数的支持向量机。

3 基于HK-SVM 的发电机温度监测分析

3.1 状态监测试验

研究过程中选用的训练数据经查验无故障停机记录，数据本身也能覆盖机组大部分正常工作区间。当机组参数位于正常工作区间时，输入与发电机轴承温度有关的4 个参数，应该能输出1 个处于正常范围的发电机轴承温度值。当发电机轴承温度发生异常，实际值与模型输出的预测值的差值会变大，通过监测这种残差的变化，对发电机驱动端轴承温度的状态进行分析。

选用上一节训练好混合核函数支持向量机对全段数据集进行测试，测试结果如图2、图3所示。

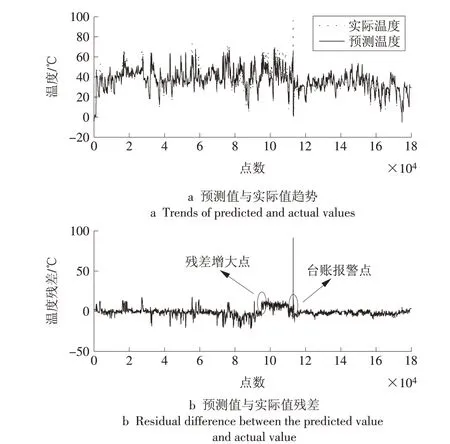
图2 #134机组发电机驱动端轴承温度趋势图（混合核函数）Fig.2 Temperature trend of the bearing at the driving end of generator in No.134 unit（hybrid kernel）

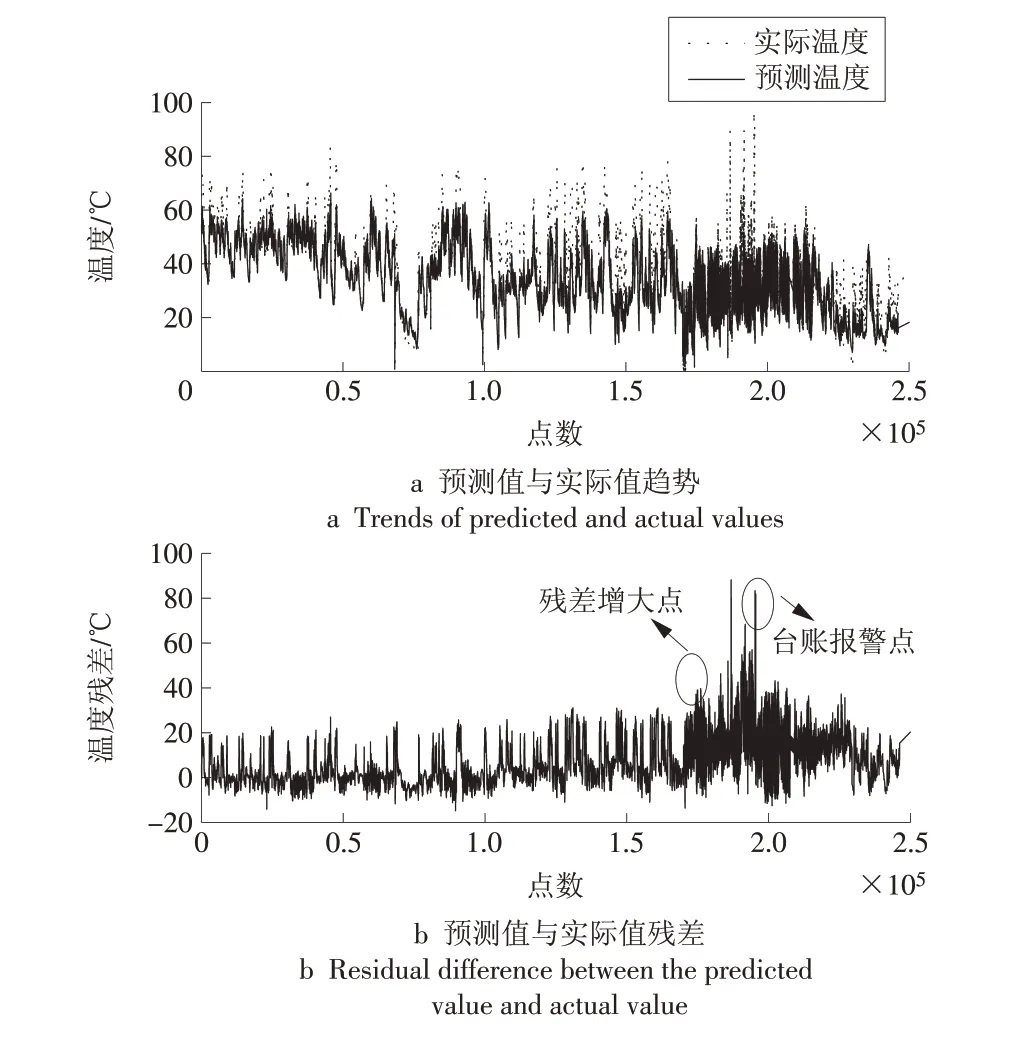
图3 #74机组发电机驱动端轴承温度趋势图（混合核函数）Fig.3 Temperature trend of the bearing at the driving end of generator in No.74 unit（hybrid kernel）

图2 和图3 中横坐标点数代表按照时间排列的数据序列位置（文中其余示意图横坐标为点数的意义也相同）。由图2 可知#134 机组发电机驱动端轴承温度预测值和实际值的情况。可见在95 000 点（对应时间为2018年12月15日）左右残差已经有增大趋势。113 429 点（对应时间为2018 年12 月28日）为台账报发电机驱动端轴承温度过高的点。结果表明残差分析能提前13 d 发现发电机驱动端轴承温度的异常变化。由图3 可知#74 机组发电机驱动端轴承温度预测值和实际值的情况。可见在175 035 点（对应时间为2019 年1 月3 日）左右残差已经有增大且波动加剧的趋势。195 233点（对应时间为2019年1月17日）为台账报发电机驱动端轴承温度过高的点。结果表明，残差分析能提前14 d 发现发电机驱动端轴承温度的异常变化。

作为对比，选用上一节训练好的高斯核函数支持向量机对全段数据进行测试，测试结果如图4、图5所示。

图4 #134机组发电机驱动端轴承温度趋势图（高斯核函数）Fig.4 Temperature trend of the bearing at the driving end of generator in No.134 unit（Gaussian kernel）

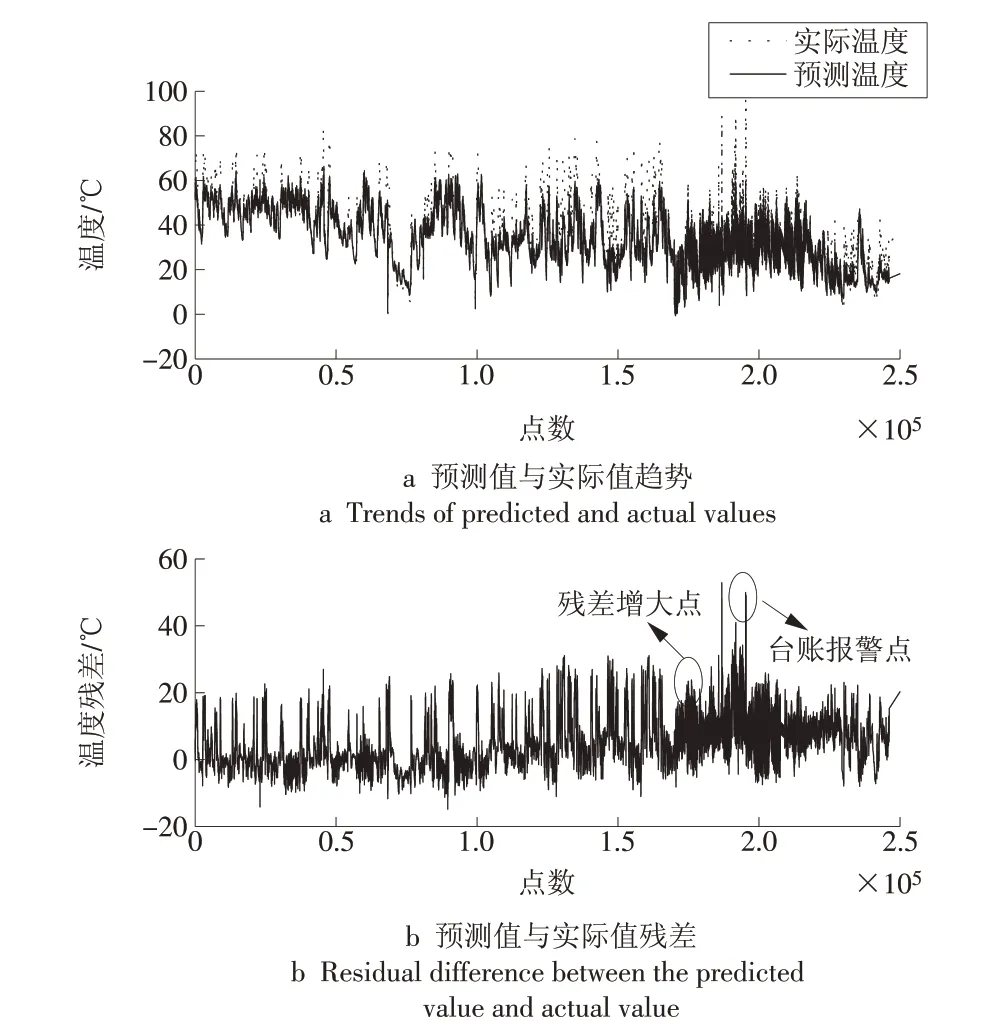
图5 #74机组发电机驱动端轴承温度趋势图（高斯核函数）Fig.5 Temperature trend of the bearing at the driving end of generator in No.74 unit（Gaussian kernel）

由图4可知#134机组发电机驱动端轴承温度预测值和实际值的情况。可见在95 000 点（对应时间为2018 年12 月15 日）左右残差没有明显增大的趋势。原因为高斯核函数支持向量机训练存在过拟合，导致轴承温度升高时残差的变化没有被捕捉到。由图5 可知#74 机组发电机驱动端轴承温度预测值和实际值的情况。可见在175 035 点（对应时间为2019 年1 月3 日）左右残差没有明显增大的趋势，并且台账报警点附近除了波动较大，使得残差分布较“稠密”外，残差绝对值并不明显区别于前期数据。同样轴承温度升高时残差的变化没有被捕捉到。

上述分析表明，混合核函数支持向量机能有效避免过拟合的情况发生，及时定位到状态异常点，综合性能优于高斯核函数支持向量机。

3.2 模型构建及统计分析

3.2.1 模型构建

从上一节研究可知，如果选用发电机历史良好的数据作为样本训练，当发电机轴承工作状态发生变化时，实际温度会偏移训练模型给出的“理想值”。通过对二者的残差进行分析可以实现发电机轴承工作异常变化的预警。选取某时间段，发电机轴承温度的残差序列

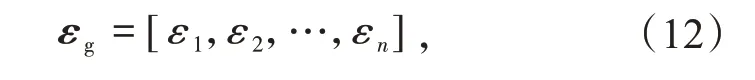
式中:εi为某时间点残差，i=1，2，…，n。

选择长度为N的滑动窗口，连续计算窗口内残差的均值及标准差

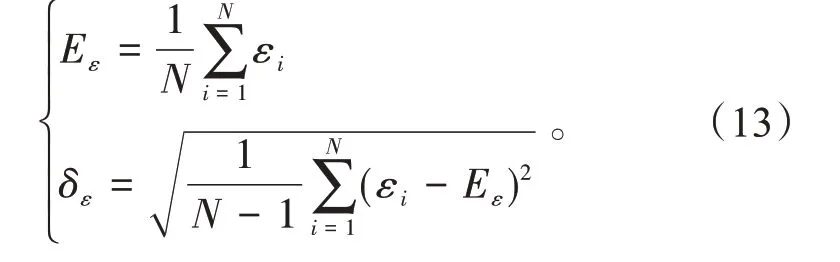
选用滑动窗口计算残差序列的原因如下:

（1）采用滑动窗口计算残差序列，便于实时监测发电机轴承温度的动态变化；

（2）滑动窗口计算残差序列的统计参数，可以抑制孤立差值增大点的影响，排除偶然因素导致的误判；

（3）通过合理的窗口设置，可以及时、迅速地发现发电机轴承工作状态的变化，消除随机影响。

除了残差均值和标准差以外，还对窗口内N个残差计算超出阈值的比例，这个阈值包括上限阈值εmax及下限阈值εmin，均根据训练数据计算得来。为了较好地符合工程实际，应用中可根据经验进行调整，即阈值标准为

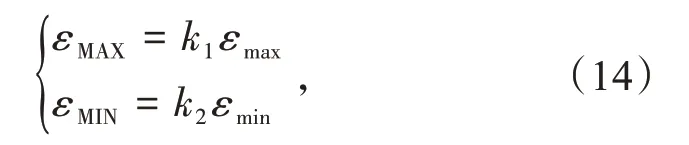
式中:k1，k2是为运行人员根据工程实际情况进行调整的系数。

3.2.2 残差统计分析

选择窗口长度为1 天（1 440 min），采样频率为1 min/次，阈值调整系数k1，k2均为1.5。对上述2 台机组的残差序列进行窗口计算，结果如图6、图7所示。

由图6 可知，#134 机组预警模型残差超限比例在80 000 点（对应时间为2018 年12 月5 日）附近开始超过50%，90 000 点（对应时间为2018 年12 月12日）后持续超过50%，大约提前23 d 实现预警。由图7 可知，#74 机组预警模型残差超限比例在150 000 点（对应时间为2018 年12 月17 日）后开始增加，在160 000点（对应时间为2018年12月24日）附近开始超过50%，大约提前24 d实现预警。

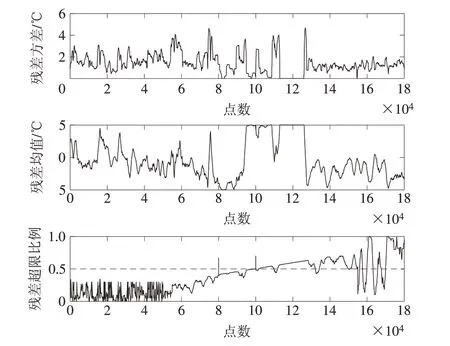
图6 #134机组发电机驱动端轴承温度残差分析Fig.6 Analysis on the temperature residual of the bearing at generator driving end in No.134 unit

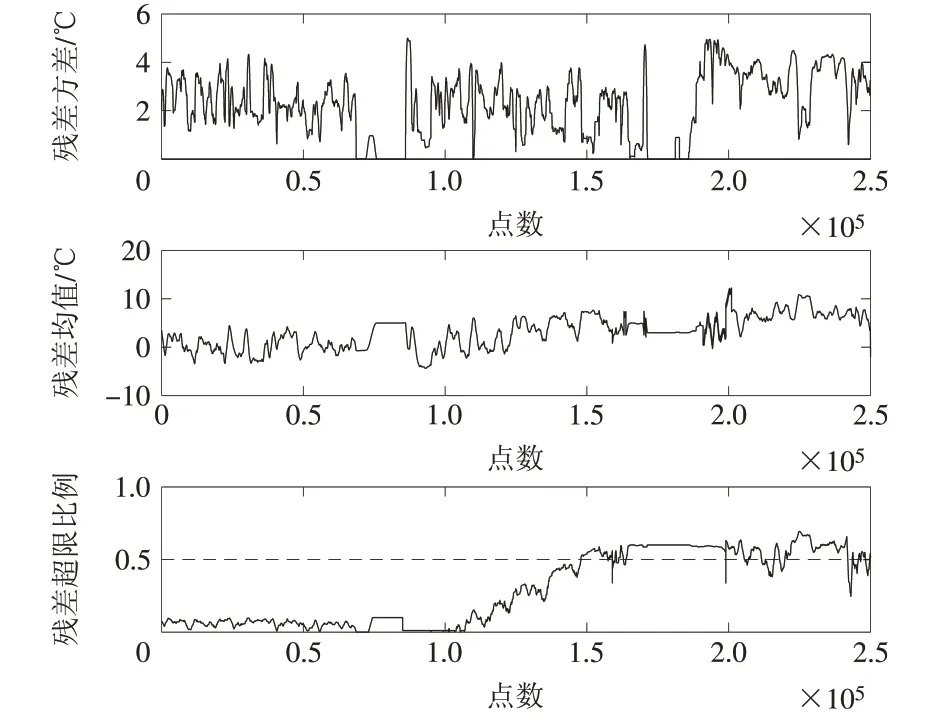
图7 #74机组发电机驱动端轴承温度残差分析Fig.7 Analysis on the temperature residual of the bearing at generator driving end in No.74 unit

上述例子证明残差超限比例检查方法可以自动实现状态变化点定位，有效预警发电机轴承的异常。

4 结论

本文针对河北某风电场1.5 MW 风电机组的SCADA 数据，利用了基于高斯核函数、多项式核函数、混合核函数的支持向量机进行训练，比较了3种核函数的各项训练指标，确定混合核函数在支持向量机训练中综合性能优于其他2类。随后使用机组历史良好的运行工况数据进行训练建模，确定合适的阈值进行预警。以2台机组发电机驱动端轴承故障为例，分析了残差超限比例的增长趋势。结果表明该模型可以提前20 d 左右发现异常，较好地实现了提前预警功能。