求解异构并行机调度问题的混合烟花算法
2020-06-16石庆民
石 庆 民
(新乡学院人事处 河南 新乡 453000)
0 引 言
异构并行机调度(Unrelated parallel machine scheduling,UPMS)是实际生产制造过程中常见的一类调度问题,具有广泛的工程应用背景,例如:云计算、半导体加工、纺织生产等[1-2]。传统的UPMS问题多以时间指标为优化目标,如makespan、提前/拖期总和等。现如今,低碳节能调度已成为实现低碳制造的重要途径,并已引起社会各界的广泛关注[3]。与此同时,快速响应客户需求也构成了企业竞争力的重要组成部分。因此,研究以能耗和延迟成本为目标的UPMS问题具有较高的理论意义和应用价值。
UPMS已经被证明是具有NP-hard性质的组合优化问题,因而设计有效的求解算法成为这一领域的研究重点。目前,求解UPMS问题的算法分为三类:精确求解算法、启发式算法和现代优化算法[4]。精确求解算法包括分枝定界、动态规划等,这类算法能够获得该问题的精确解,但实用性较弱,无法在合理的时间内求解中大规模算例[5]。启发式算法是利用调度规则对问题进行快速求解,具有运算时间短、求解精度较高等优点,但该类算法对问题的设置具有严格限制,通用性较差[6]。近年来,随着现代优化算法的快速发展,学者们逐步开始使用智能算法来求解这一问题,相关算法包括遗传算法、禁忌搜索算法、模拟退火算法等。研究表明,这类算法能够在较短的时间内获得中大规模算例的满意解,且具有较强的通用性[7]。因此,本文基于基本烟花算法(Firework algorithm,FWA)设计了改进算法用于求解考虑节能的异构并行机调度问题。
FWA是Tan等[8]提出的新型现代优化算法,属于群智能优化算法,该算法受烟花爆炸行为的启发通过烟花爆炸生成火花这一过程实现迭代进化。FWA具有收敛速度快、求解精度高等优点,目前已经在数据挖掘、神经网络训练、车辆路径规划等多个方面获得了成功应用[9]。即便如此,FWA在中大规模测试问题的求解过程中仍然存在易陷入局部最优、收敛速度慢等缺点。因此,提升FWA的寻优性能仍然是该邻域的一个重难点。
基于以上研究内容,本文考虑一类加工时间可控的并行机调度问题,并以能耗和拖期惩罚成本为优化目标构建了混合整数线性规划(Mixed Integer Linear Programming,MILP)模型。算法设计中创建了特定的编解码方法以表示问题的解,同时融入了反向学习初始化方法以提升初始解的质量,并构建了基于变邻域搜索算法的局部优化流程用以强化基本算法的寻优性能。仿真测试中,利用正交实验对算法参数进行校验,并将HFWA的优化结果与多种经典的优化算法进行比较,测试结果验证了HFWA的可行性和有效性。
1 问题模型
1.1 问题描述
在UPMS-ETC问题中,假设有n个任务需要在m台机器上加工,各个机器存在多种不同的加工速度,各机器在不同加工速度下的能耗存在差异性。此外,已知各个订单的交货期,晚于规定的时间交货将会产生延迟惩罚成本。
本文以最小化所有任务的加工能耗成本和延迟惩罚成本总和为目标,决策内容包含以下三点:1) 各个机器所加工的任务集合;2) 各个机器上加工任务的排序;3) 各任务的加工速度。
1.2 数学建模
为了构建UPMS-ETC问题的MILP模型,定义以下数学符号。
问题参数:
m:机器总数,i∈{1,2,…,m}。
n:任务总数,v∈{1,2,…,n}。
l:加工位置编号,l∈{1,2,…,n},各台机器均设有n个加工位置。
Qi:机器i可选的速度类别总数,s∈{1,2,…,Qi}。
lv:任务v的标准加工时间。
ris:机器i以第s种加工速度的取值。
tvis:任务v在机器i上以速度ris加工时相应的加工时间,tvis=lv/ris。
eis:机器i在单位时间内以速度ris运行所产生的能耗。
dv:任务v的交货期。
Cv:任务v的完成时间。
τv:任务v的延误时间,τv=max{0,Cv-dv}。
μv:任务v单位时间的延误惩罚成本。
决策变量:
xvils:0-1变量,任务v在机器i以速度ris进行加工,xvils取值为1;否则,xvils取值为0。
Bil:机器i上位置l任务开始加工的时间。
基于以上问题描述和符号定义,构建了UPMS-ETC问题的MILP模型。
目标函数:
(1)
约束条件:
(2)

(3)
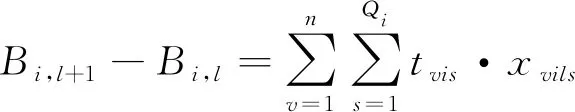
(4)
τv≥Bi,l+tvis·xvils-(1-xvils)·M-dj
i∈{1,2,…,m},s∈{1,2,…,Qi},v∈{1,2,…,n},
l∈{1,2,…,n}
(5)
τv≥0v∈{1,2,…,n}
(6)
xvils∈{0,1},i∈{1,2,…,m},s∈{1,2,…,Qi},
v∈{1,2,…,n},l∈{1,2,…,n}
(7)
式(1)表示目标函数,即所有任务的加工能耗成本和延误惩罚成本之和;式(2)用于确保各个加工任务所选的加工机器、加工位置和加工速度的唯一性;式(3)表示各台机器上每个加工位置处最多只能安排一个加工任务;式(4)用于计算机器i上位置l处加工任务的开始时间;式(5)-式(6)用于计算各个任务的延误时间;式(7)定义了决策变量的取值范围。
2 基本烟花算法
FWA以烟花表示待优化问题的解,并通过烟花爆炸生成火花这一过程迭代进化。首先依据各烟花个体的评价函数值计算相应的爆炸火花数目和爆炸半径数值;其次,采用均分分布和高斯分布生成新个体;最后,利用选择规则构建新种群以进入下一次迭代。具体实现步骤归纳如下:
Step1初始化算法参数,利用随机方法构建初始种群并对每个烟花个体进行评价。
Step2依据评价函数计算当前种群中各个烟花的爆炸火花数目和爆炸半径。
Step3利用均分分布和高斯分布生成爆炸火花和高斯变异火花。
Step4利用烟花、爆炸火花和高斯变异火花构建候选种群,并依据筛选规则生成新种群。
Step5判断是否满足终止条件。若满足则停止迭代搜索并输出当前最优解;否则,转Step 2。
FWA的核心内容包含以下四点:(1) 计算爆炸火花数目和爆炸半径;(2) 生成爆炸火花;(3) 生成高斯变异火花;(4) 基于选择规则构建新种群。
计算爆炸火花数目和爆炸半径:以N表示烟花数目,以xi表示当前种群中的第i个烟花,N个烟花数目生成的爆炸火花总数记为SN。以最小化问题为例,对于烟花xi,以符号fi表示其评价函数值,以Si和Ri表示由xi生成的爆炸火花数目和相应的爆炸半径。Si和Ri的计算公式归纳如下:
(8)
(9)
式中:fmax和fmin分别表示当前烟花种群中最大和最小的评价函数值;A表示基本爆炸半径,需要预先设定;ε为机器最小值,用以避免除零操作。同时,为了对上述Si计算公式做修正以确保优势烟花个体生成的火花数不过多、劣势烟花个体生成的火花数不过少,修正公式为:
(10)
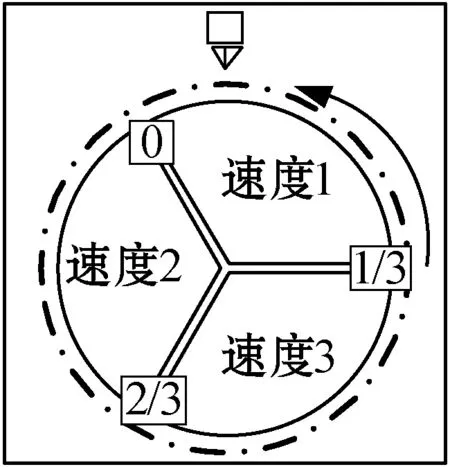
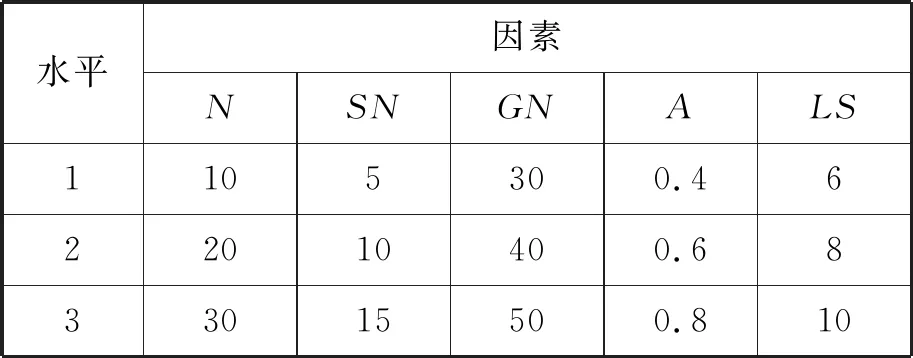
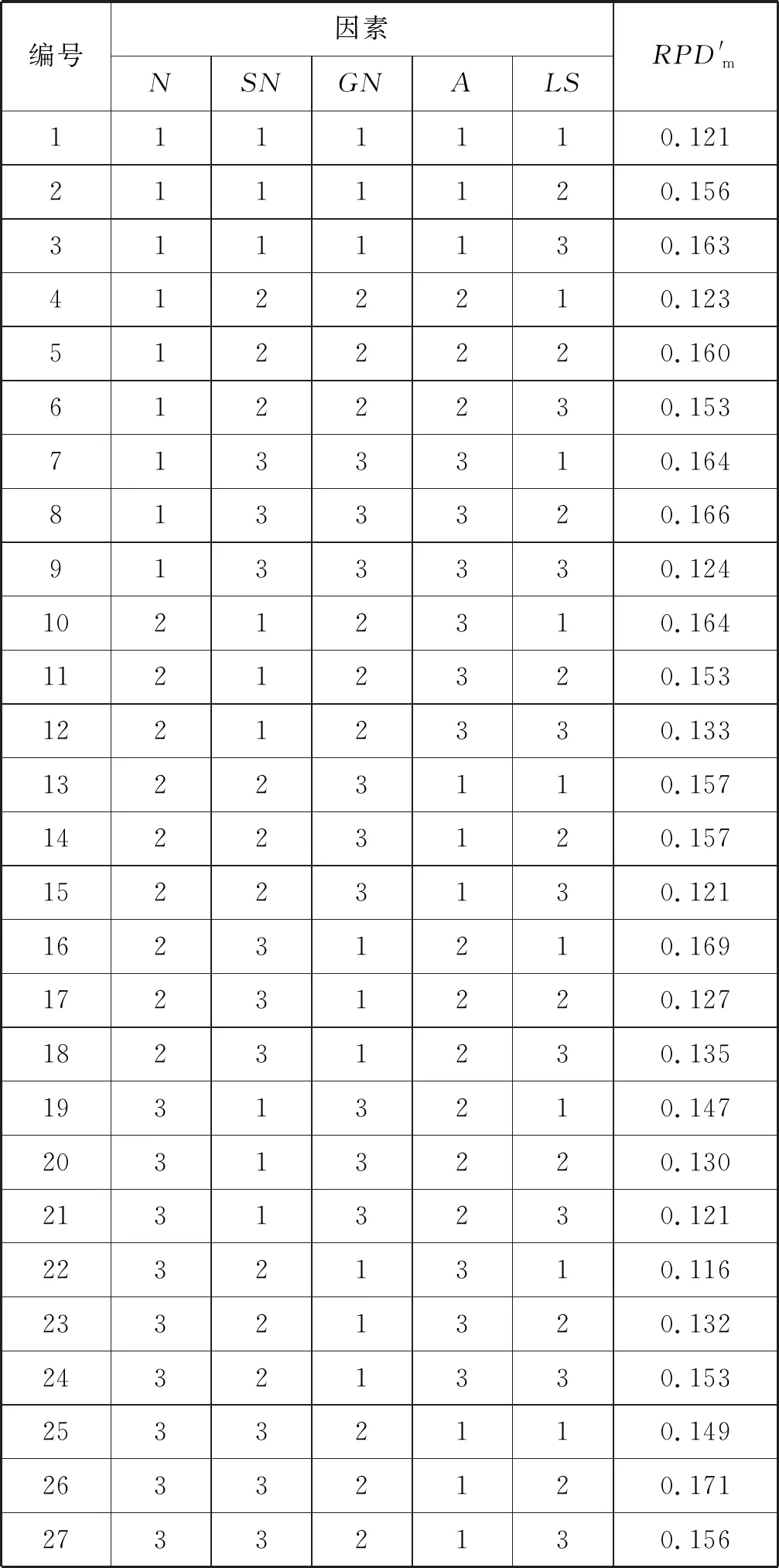
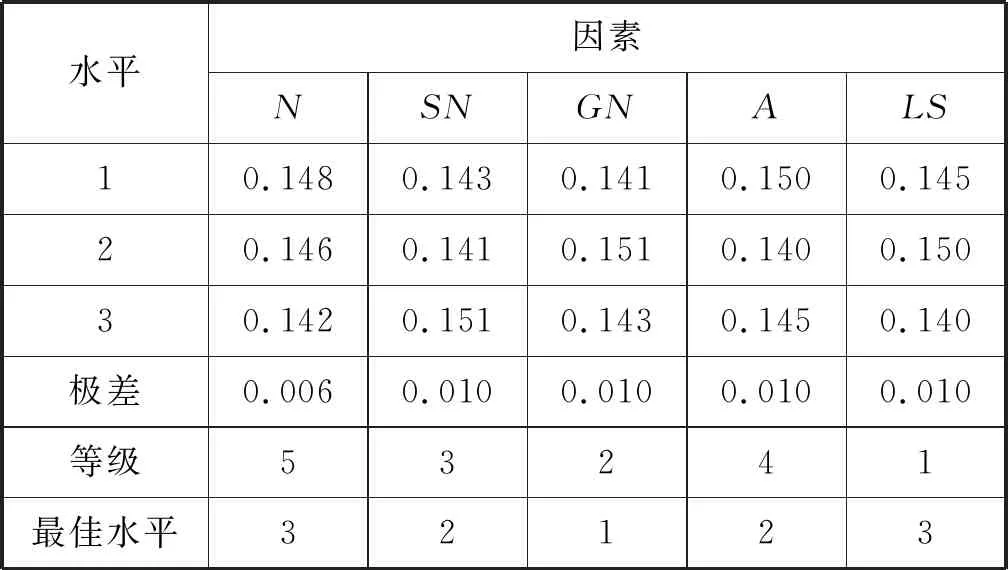
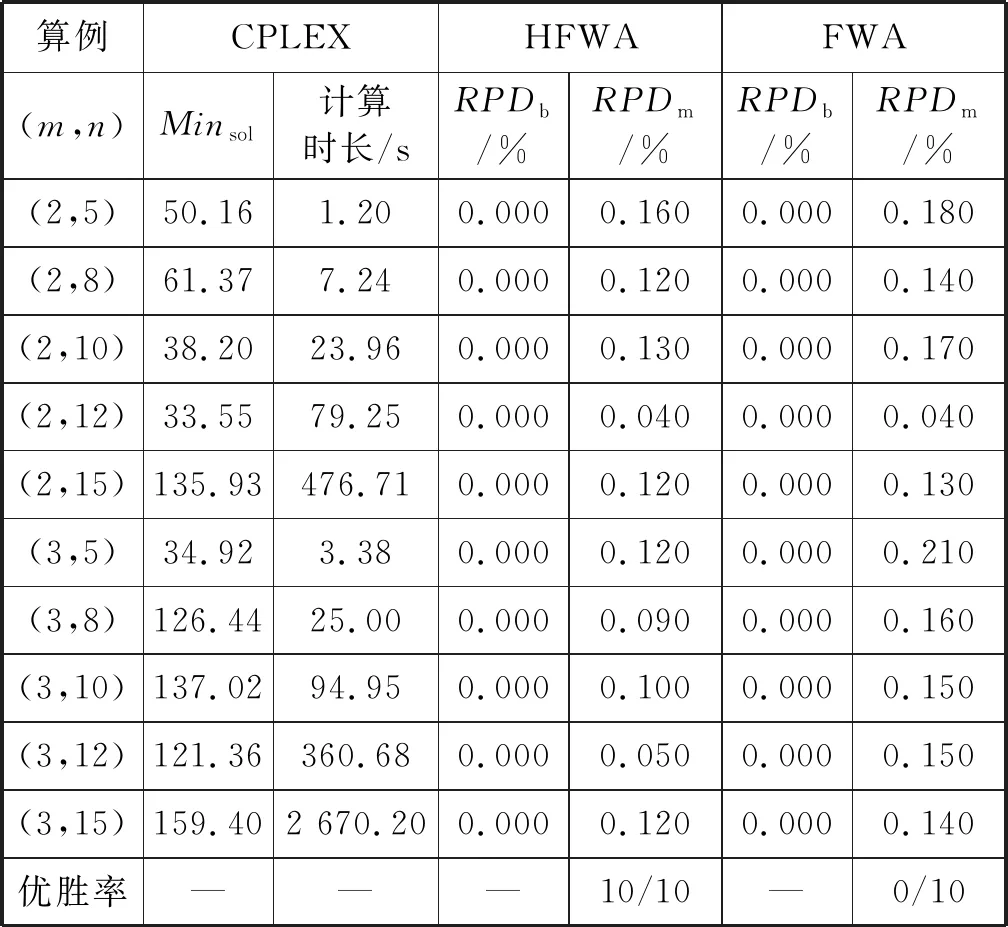
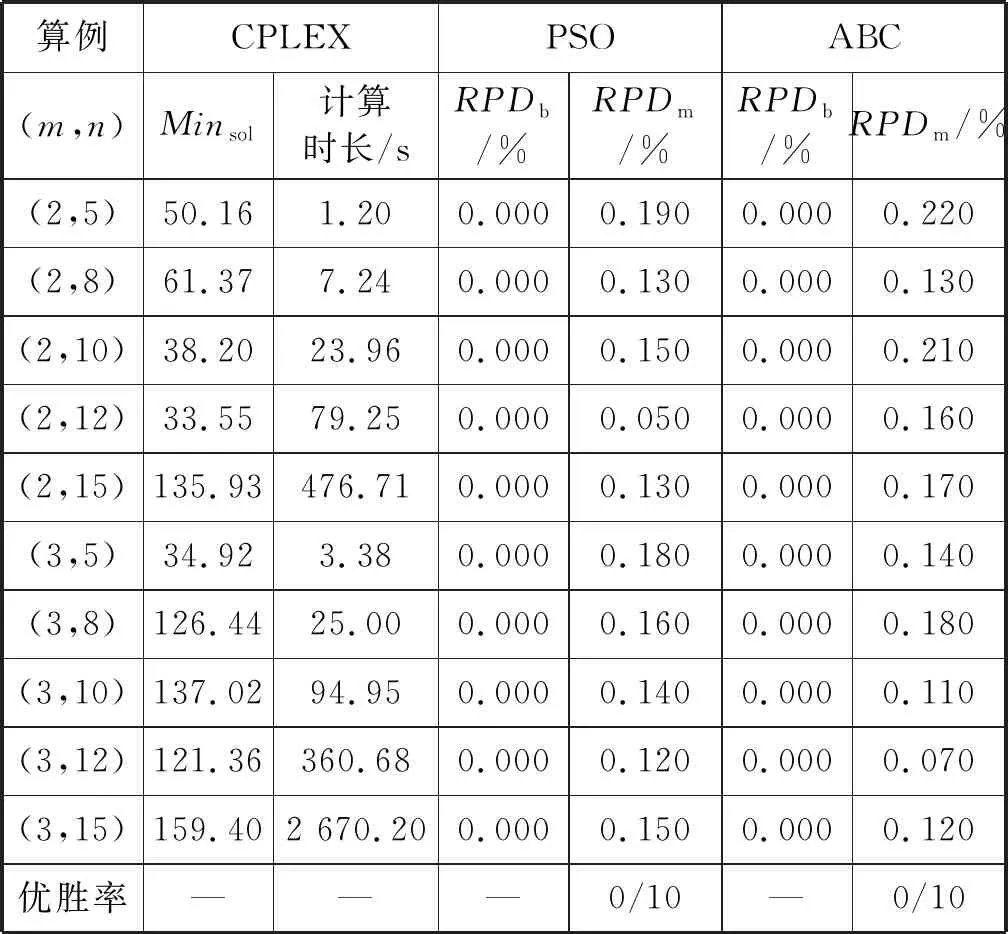
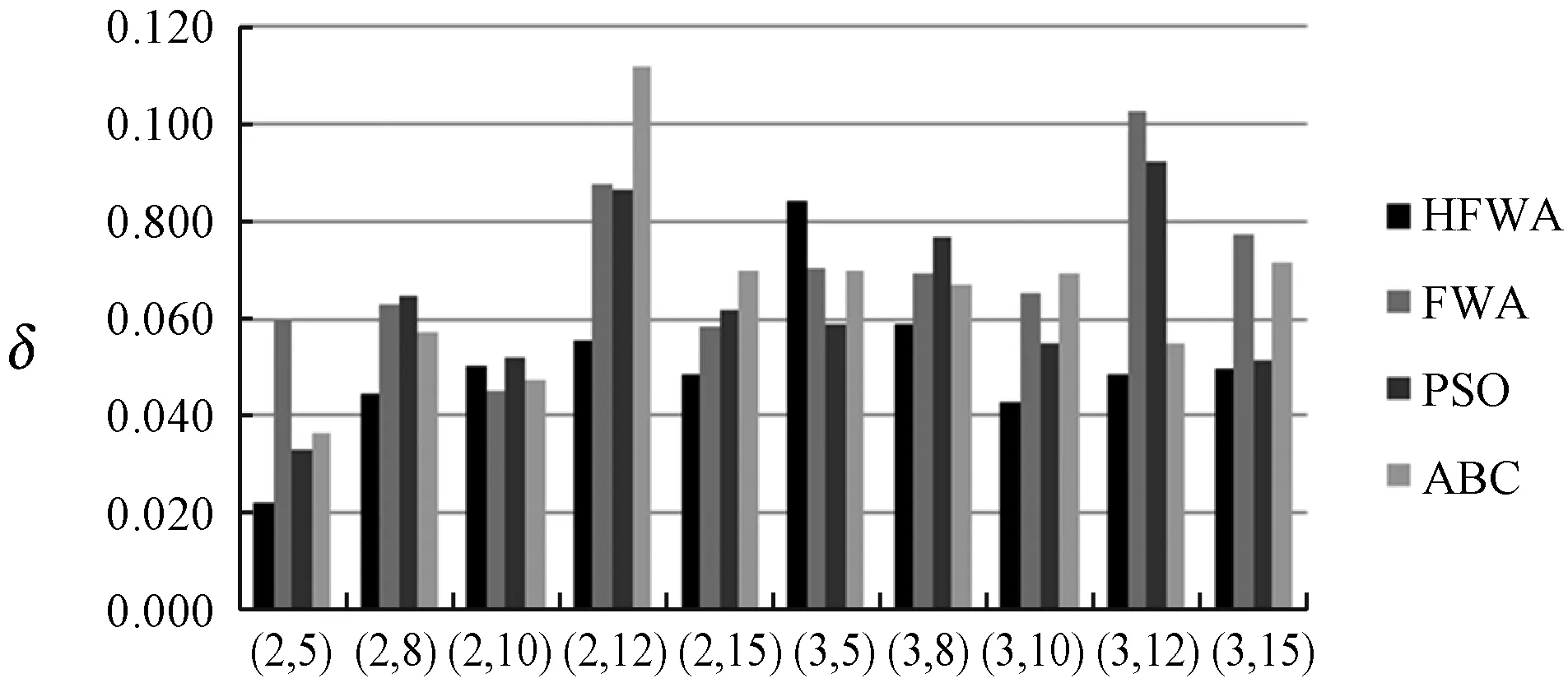
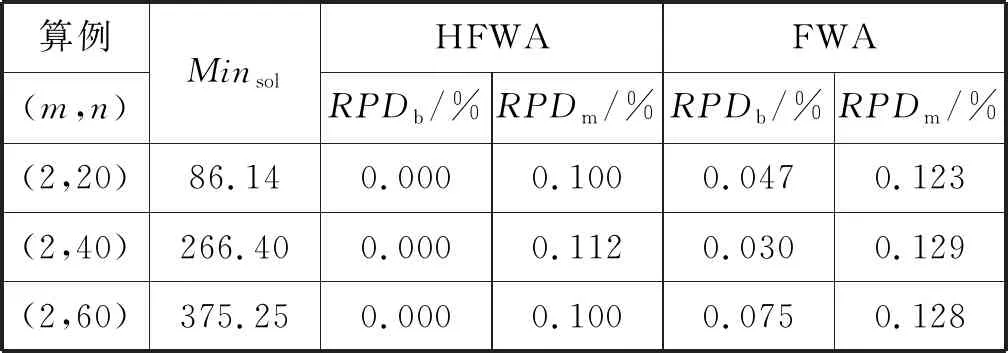
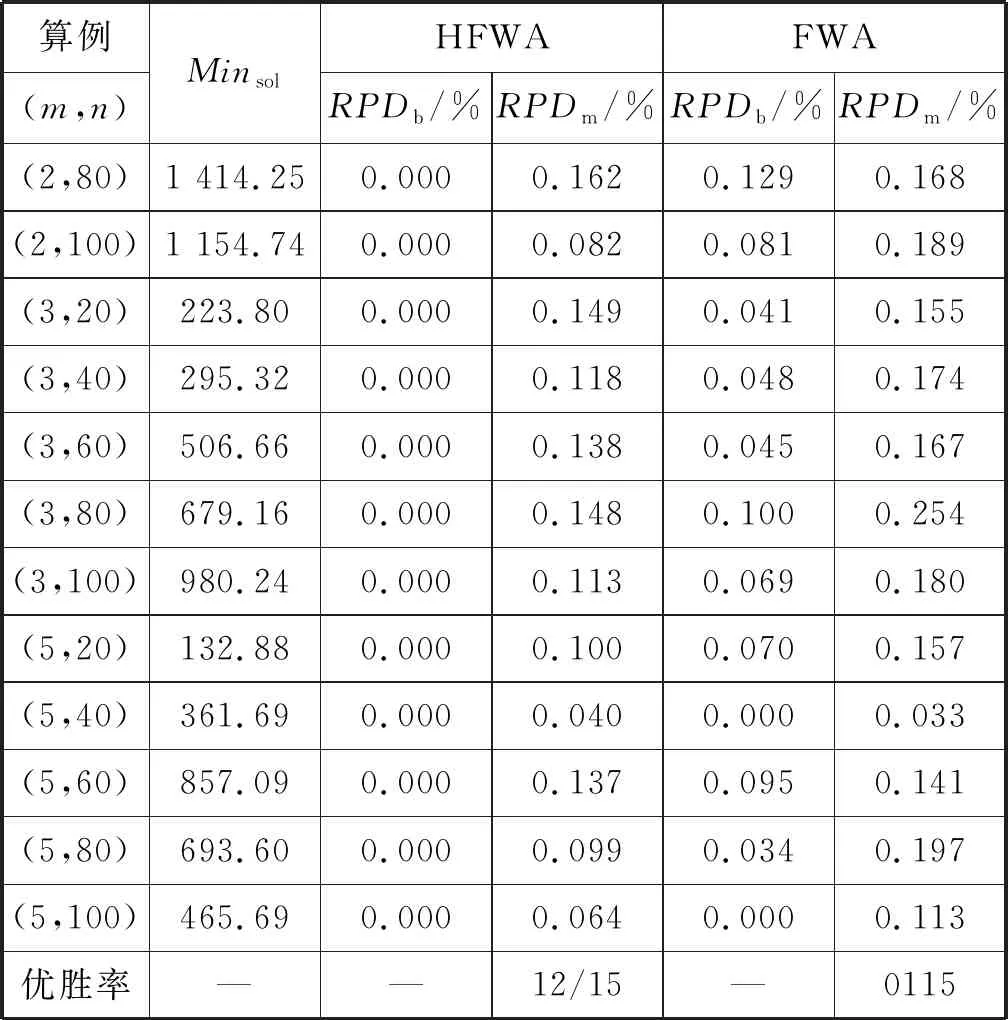
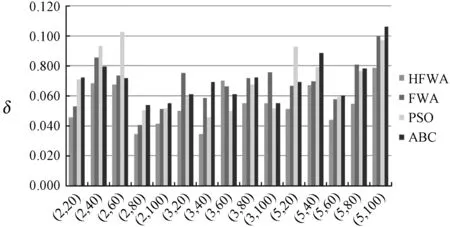
式中:常数a和b满足0 生成爆炸火花:依据计算所得Si和Ri值,生成当前烟花个体xi对应的爆炸火花。以D表示待优化问题的维度,随机选取维度集合{1,2,…,D}的一个子集Dz,利用式(11)更新xi的相应维度的编码数值取值生成新个体。 xiz←xiz·rand(-1,1) ∀Z∈Dz (11) 式中:rand(-1,1)表示区间[-1,1]的均分分布。 生成高斯变异火花:首先,利用随机的方法从当前种群中选择GN个烟花;其次,对所选的各个烟花,随机选择一些维度并利用高斯分布进行更新,以Dz表示所选烟花xi的一个维度子集。相应的更新公式如下: xiz←xiz·N(1,1) ∀Z∈Dz (12) 式中:N(1,1)表示均值为1、方差为1的高斯分布。 基于选择规则构建新种群:首先,将当前烟花种群、爆炸火花种群和高斯变异火花种群合并,将其中最优个体直接选入下一代种群;其次,依据轮盘赌规则选出其余N-1个解构建新种群。以K表示候选种群规模,则其中第i个烟花解xi被选择的概率取值为: (13) 式中:d(xi,xj)表示个体xi和xj的距离。 此外在算法进化中,变异操作往往使得新生成的烟花个体中某些维度的取值在规定的范围之外,为此采用如下公式修复不可行解: (14) 为了有效地求解UPMS-ETC问题的数学模型,本文基于标准FWA构建了HFWA。算法设计了双层编码方式和解码方法,用于表示UPMS-ETC问题的解;融入了反向学习初始化方法,致力于提升初始解的质量;构建了基于变邻域搜索算法的局部优化流程,用以强化基本FWA的寻优性能。 标准FWA采用实数编码方式,无法直接用于求解离散组合优化问题。为此,本文结合问题的性质,构建了UPMS-ETC问题的编码与解码机制。 编码过程:采用双层实数编码,两层编码长度值均为n;编码第一层用于各个机器的加工任务序列,各维度编码的取值范围为[1,m+1);编码第二层用于确定各任务在机器上的加工速度,各维度编码的取值范围为[0,1]。 UPMS-ETC问题需要决策以下三点:(1) 各个机器所加工的任务集合;(2) 各个机器上加工任务的排序;(3) 各订单的加工速度。相应的解码过程归纳如下: • 取第一层编码的整数部分,用于确定各任务的加工机器编号,进而得到各个机器的加工任务集合。 • 基于各个机器的加工任务集合,取第一层编码的小数部分用于确定各个机器上的任务加工顺序,小数部分取值小所对应的加工任务优先加工。 • 针对各个机器,构建选择加工速度的轮盘赌模型,并依据轮盘赌规则确定各个机器所分得的加工任务的加工速度。如图1所示,假设某一机器共有三种不同的加工速度,则当该任务对应第二编码的数值在区间[0,1/3)上,则采用加工速度1;若其数值在区间[1/3,2/3)上,则采用加工速度2;若其数值在区间[2/3,1]上,则采用加工速度3。 图1 基于轮盘赌规则的加工速度选择 为了清晰地说明该编解码方法,给出如下算例:任务总数为8,机器总数为3,机器1和机器3具有3种加工速度,机器2具有两种加工速度。已知如下编码:第一层(3.19,1.80,2.97,2,90,1.47,1.35,2.45,3.78),第二层(0.13,0.05,0.84,0.93,0.20,0.48,0.15,0.83),图2给出了完整的解码过程。 (a) (b) (c) 基本FWA采用随机的方法构建初始种群,一定程度上限制了算法的优化性能。为此,本文利用反向学习初始化方法构建初始解,力求提升初始种群的质量[10]。该方法的基本思路为:借助随机方法生成多个初始解和相应的反向解,结合评价函数进行筛选,选取较优的解构造初始种群。结合以上描述,反向学习初始化方法的实现步骤归纳如下: Step1令i←1,d←1,转Step 2。 Step2若i≤N,转Step 3;否则,转Step 7。 Step3若d≤D,转Step 4;否则,转Step 5。 Step5令d←d+1,若d>D,转Step 6,否则,转Step 3。 Step6令i←i+1,转Step 2。 在算法迭代后期,基本FWA存在寻优性能不佳、易陷入局部最优的缺点。为此,本文基于变域搜索算法构建了局部优化流程,力求增强基本FWA的性能[11]。 变域搜索算法通过系统地改变当前解以拓展算法的搜索范围,进而获得待优化问题的局部最优解;同时,基于此局部最优解,再次系统地进行解空间的拓展,力求获得另一局部最优解。图3为变邻域搜索算法的示意图。 图3 变邻域搜索算法示意图 邻域结构设计构成了变邻域搜索算法的一项核心内容,对于当前研究的PMS-CPT问题,本文采用交换和翻转两种邻域结构实现从当前解到新解的变换,具体描述如下: • 交换变异:随机选择当前解编码的两处位置,交换这两处位置上的编码数值生成新解。 • 翻转变异:随机选择当前解编码的两处位置,翻转这两处位置间的编码数值生成新解。 图4所示的邻域结构示意图清晰地说明了以上两种变异算子。当前编码方法中,编码第一层用于各个机器的加工任务序列,编码第二层用于确定各任务在机器上的加工速度。因此,以上邻域变换能够对改善的解产生扰动,探索其周围的解。 图4 邻域结构示意图 由编解码方法可知,编码第一层用于各个机器的加工任务序列,编码第二层用于确定各任务在机器上的加工速度。因此,以上邻域变换能够对当前解产生扰动,从而探索当前解附近的其他解。 Step1初始化算法各参数,利用反学习初始化方法生成初始解,并对每个烟花个体进行评价。 Step2依据评价函数计算当前种群中各个烟花的爆炸火花数目和爆炸半径。 Step3利用均分分布和高斯分布生成爆炸火花和高斯变异火花。 Step4利用烟花、爆炸火花和高斯变异火花构建候选种群,并依据筛选规则生成新种群。 Step5对于各个烟花个体,利用基于变域搜索算法的局部优化流程进一步改善其性能。 Step6判断是否满足终止条件。若满足则停止迭代搜索并输出当前最优解;否则,转Step 2。 在MATLAB 2015a平台上进行仿真测试,设备参数为1.6 GHz、内存8 GB、Intel Core i5-8250U CPU,并利用CPLEX 12.4和CPLEX-MATLAB接口求解UPMS-ETC问题的MILP模型,CPLEX最大求解时间设置为3 600 s。考虑到难以从现有文献中获取与当前UPMS-ETC问题相似的测试算例,本文依据相关机器调度问题生成方法采用随机方法构建测试算例集,具体包括小规模和中大规模两类算例[12]。 在小规模算例中,机器数目m∈{2,3},任务数目n∈{5,8,10,12,15},共计10个算例;在中大规模算例中,机器数目m∈{2,3,5},任务数目n∈{20,40,60,80,100},共计15个算例。对于算例(m,n),其他参数设置如下: • 任务的标准加工时间lv在均分分布U(50,200)上随机产生; • 任务v单位时间的拖期成本μv的数值在均分分布U(0.1,1)上随机产生; • 加工速度类型总数Qi均设置为5,加工速度ris在均分分布U(1,20)上随机产生; • 各机器在不同速度下的能耗参数eis在均分分布U(0.1,2)上随机产生,且对于同一机器而言,加工速度越快,其能耗越高; • 任务v的交货期dv在均分分布U(D,3·D)上随机产生,参数D的计算公式为: (15) 为了验证算法的有效性,将本文提出的HFWA与多种优化算法进行比较,包括:FWA、粒子群算法(Particle swarm optimization, PSO)和蜂群算法(Artificial bee colony, ABC)。其中,与基本FWA进行对比用于加入改进方法后对标准算法性能的改善;与此同时,PSO与ABC算法作为目前较优秀的优化算法,其进化机理和HFWA存在些许差异,因而同这两种算法进行对比能够凸显HFWA的竞争力。对于各个测试算例,以上四种算法均独立运行15次,对测试结果进行统计分析,采用最优相对偏差(RPDb)和平均相对偏差(RPDm)作为评价指标[13],公式定义如下: (16) (17) 表1 正交试验参数设置 表2 正交试验仿真结果 表3 正交试验极差分析 由以上测试结果可知,局部搜索参数LS和高斯变异参数GN对HFWA的性能影响最大,其次是参数爆炸火花参数SN和基本爆炸半径A,最后是种群规模N。据此可知这表明局部优化算子和高斯变异对算法的优化性能具有重要影响,因而需要合理设置LS和GN,若取值过大将使算法过分注重局部搜索,若取值过小则弱化了算法的挖掘能力。与此同时,其余三个参数也需要进行合理设置,才能使HFWA达到最优的搜索性能。各参数取值归纳如下:N=30,SN=10,GN=30,A=0.6,LS=10。 类似地,借助正交实验进行小规模情况下的HFWA参数校验,算法取值归纳如下:N=10,SN=5,GN=20,A=0.6,LS=5。为了确保对比的公平性,FWA各参数取值与FWFA相同,PSO和ABC的种群规模与HFWA相同,其余参数采用相似方法进行校验。小规模情形下PSO和ABC的其他参数设置如下:PSO权重系数为1.0,全局学习参数取值为1.5,自身历史最优学习参数2.0,ABC侦察蜂步数为10;中大规模情形下PSO和ABC的其他参数设置如下:PSO权重系数为0.95,全局学习参数取值为1.8,自身历史最优学习参数2.0,ABC侦察蜂步数为20。 结合以上参数校验的结果,分别采用HFWA、FWA、PSO和ABC四种优化算法对各个小规模算例进行求解,测试结果见表4和表5。其中Minsol表示CPLEX所得目标函数的最优解,计算时长则为CPLEX求解各个算例的耗时。表格最后一行优胜率表示某一测试算的RPDm指标在所有测试算例中获得最优性能的比率,例如“2/10”表示对应的算法在共计10组测试算例中两次获得最优RPDm值。此外,对于各个算例,以符号表示某一算法15次运行结果相对偏差百分比的标准差,图5给出了各算法在不同算例中的δ取值。 表4 小规模算例测试结果1 表5 小规模算例测试结果2 图5 小规模算例方差对比 由测试结果可知,在小规模算例中,各个测试算法的性能都较为良好,RPDb指标均能达到0,即能够获得小规模算例的精确解。就RPDm指标而言,HFWA的性能最优,其优胜率为10/10。由图5可知,HFWA在多数情形下具有较小的δ值,表明其具有较强的鲁棒性,算法优化结果更为稳定。此外,由CPLEX计算时长参数可知,随着问题规模的扩大,求解MILP模型所需的时间急剧增加,算例(3,15)的计算时长达到2 670.20 s,因此有必要设计高效的智能算法来求解UPMS-ETC问题。 进一步地,利用HFWA、FWA、PSO和ABC四种测试算法求解各种大规模算例,测试结果见表6和表7。其中Minsol表示表示四种算法在共计60次仿真中所得最优解。对于各个算例,图6给出了各算法在不同算例中的δ取值。 表6 中大规模算例测试结果1 续表6 表7 中大规模算例测试结果2 图6 中大规模算例方差对比 由测试结果可知,四种算法中,HFWA表现值最优秀,其RPDb指标均为0,表明HFWA能够获得各个算例的已知最优解。就RPDm指标而言,HFWA的性能最优,其优胜率为12/15,表明本文算法在15组测试算例中12次获胜;在剩余三组算例中,HFWA的表现同样较为优秀,与最优RPDm值较为接近。此外,由图6可知,HFWA在多数情形下具有较小的δ值,表明算法优化结果更为稳定,即算法具有较强的鲁棒性。 本文以加工时间可控的UPMS问题为研究对象,构建了该问题的MILP模型,并提出了HFWA求解算法以最小化作业期间的能耗和延迟惩罚成本总和。算法设计中,创建了特定的编解码方法以表示问题的解,同时融入了反向学习初始化方法以提升初始解的质量,并构建了基于变邻域搜索算法的局部优化流程用以强化基本算法的寻优性能。在实验部分,借助正交实验对算法参数进行校正,并将HFWA与多种智能优化算法进行对比,结果表明本文构建的HFWA能够快速、有效地求解UPMS-ETC问题,并具有显著的优越性。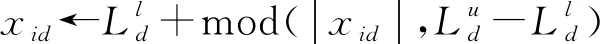
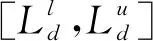
3 混合烟花算法
3.1 编码与解码

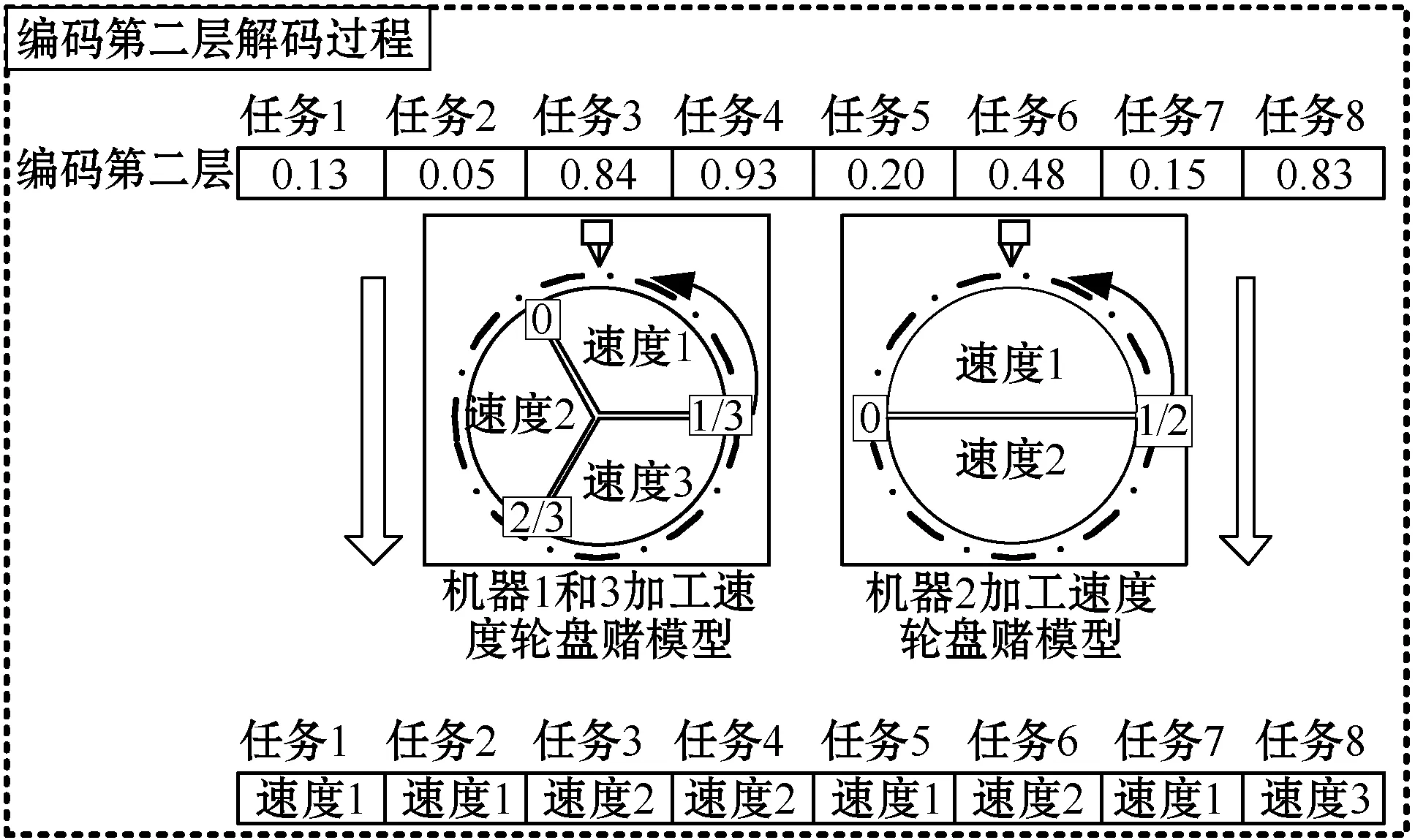
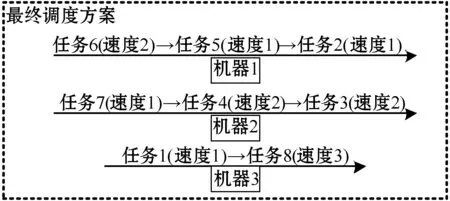
3.2 反向学习初始化方法
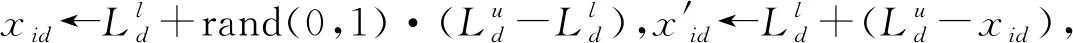
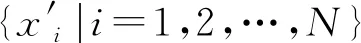
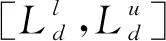
3.3 基于变域搜索算法的局部优化流程
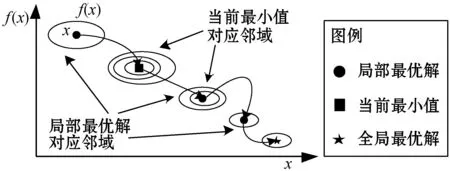
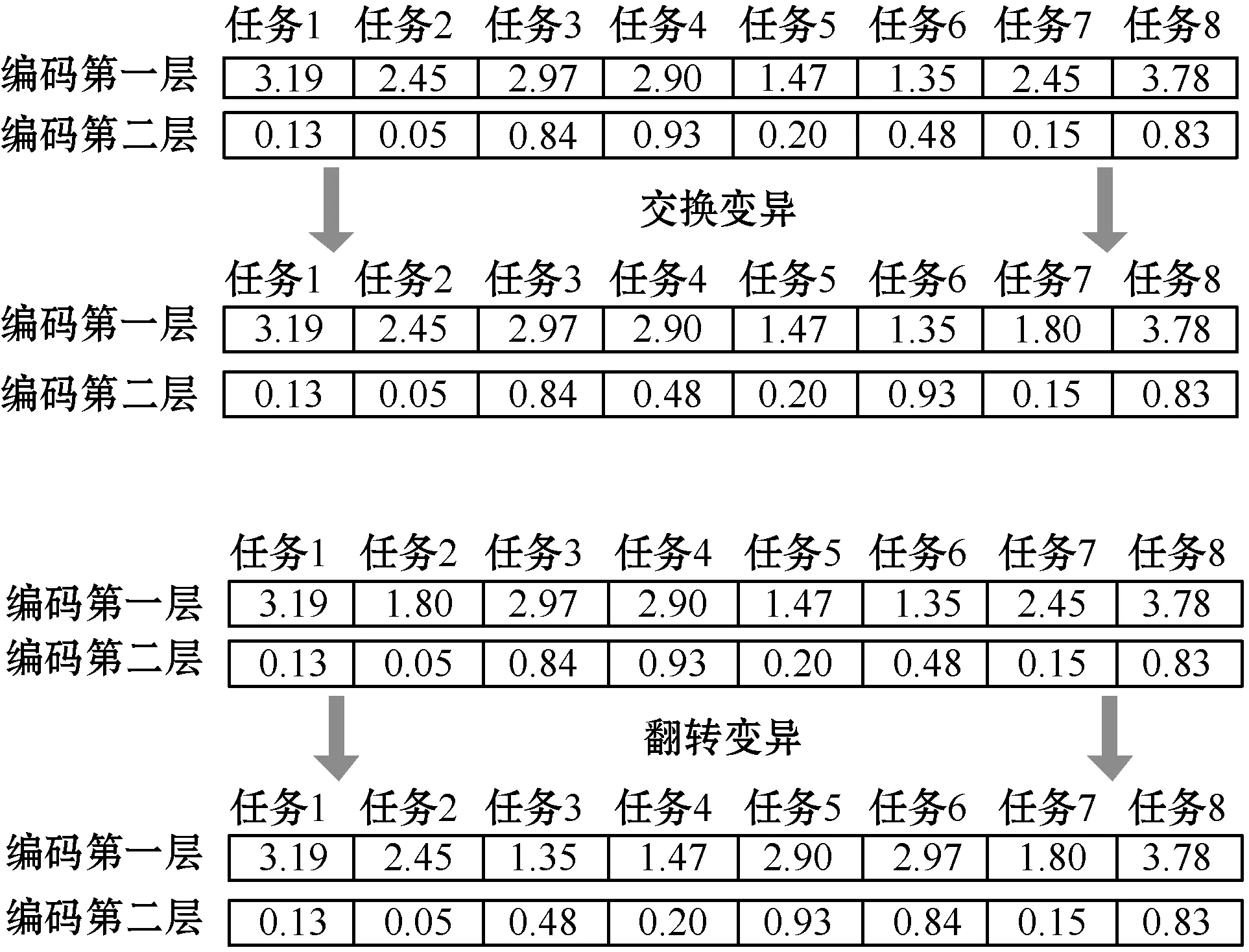
3.4 混合烟花算法流程
4 仿真测试
4.1 实验准备
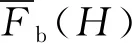
4.2 参数校验
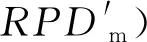
4.3 算法对比

5 结 语
