小学数学书面测验试题命制的几个注意点
2020-06-15陈六一
陈六一

摘要:基于《普通高中数学课程标准(2017年版)》提出的命题原则,小学数学书面测验试题的命制需要注意以下几点:考查核心素养,聚焦本质理解,融入文化元素,赋予分值多义。
关键词:数学试题课程标准核心素养本质理解文化元素
教学评价是教学活动的重要组成部分,可以考查学生学习的成效,进而考查教师教学的成效。通过考查,可以诊断学生学习过程中的优势与不足,进而诊断教师教学过程中的优势与不足;通过诊断,可以改进学生的学习行为,进而改进教师的教学行为。
书面测验是教学评价的重要形式,测验试题是教学评价的重要工具。对于测验试题的命制,《普通高中数学课程标准(2017年版)》指出:“命题应依据学业质量标准和课程内容,注重对学生数学学科核心素养的考查,处理好数学学科核心素养与知识技能的关系……”“考查内容应围绕数学内容主线,聚焦学生对重要数学概念、定理、方法、思想的理解和应用……融入数学文化。”“命题时,应有一定数量的应用问题,还应包括开放性问题和探究性问题,重点考查学生的思维过程、实践能力和创新意识……评分应遵循满意原则和加分原则,达到测试的基本要求视为满意,有所拓展或创新可以根据实际情况加分。”作为基础教育领域当下最新的课程标准,其基本理念对小学数学教学无疑也有着重要的指导价值。基于上述命题原则,小学数学书面测验试题的命制需要注意以下几点:
一、考查核心素养
命题时,要依托相关的问题情境,既关注学生知识技能的掌握,更关注数学学科核心素养的形成和发展,要把对知识技能掌握的考查和对数学学科核心素养达成的考查结合起来。下面分别就数学建模素养和数据分析素养的考查举例进行说明。
例1某大学生计划暑期勤工俭学,以挣取下学期的生活费。他看到一家餐厅招聘小时工的启事,标注着“每天的薪资待遇=基本工资+时薪×时间”,并给出了参照表,如表1。
那么根据表格,这家餐厅每天的基本工资是元 ,时薪是元;如果工作3天,共获得薪资285元,那就意味着平均每天工作了小时。
“从现实生活或具体情境中抽象出数学问题,用数学符号建立方程、不等式、函数等表示数学问题中的数量关系和变化规律,求出结果、并讨论结果的意义”,数学建模素养便一步步清晰可见。例1便这样考查着学生的数学建模素养。根据表1中每一列的数据,可以列出诸如50÷2、80÷4、110÷6等的算式,認为求得的是每小时的工作报酬,即时薪,然而,结果呈现出时薪是有差异的。这就逼着学生进一步厘清,50元、80元、110元等工作报酬中包含着两种不变量:一是基本工资,二是时薪。这就需要学生从整体上观察数据:横着看,每增加2小时工作量,报酬增加30元,或者每增加1小时工作量,报酬增加15元。由此能够求出时薪是15元。接着,用时薪乘工作时间,再用工作报酬减去相应结果,就可以得到基本工资,即50-2×15、80-4×15、110-6×15……同样,不同的式子可以相互验证。
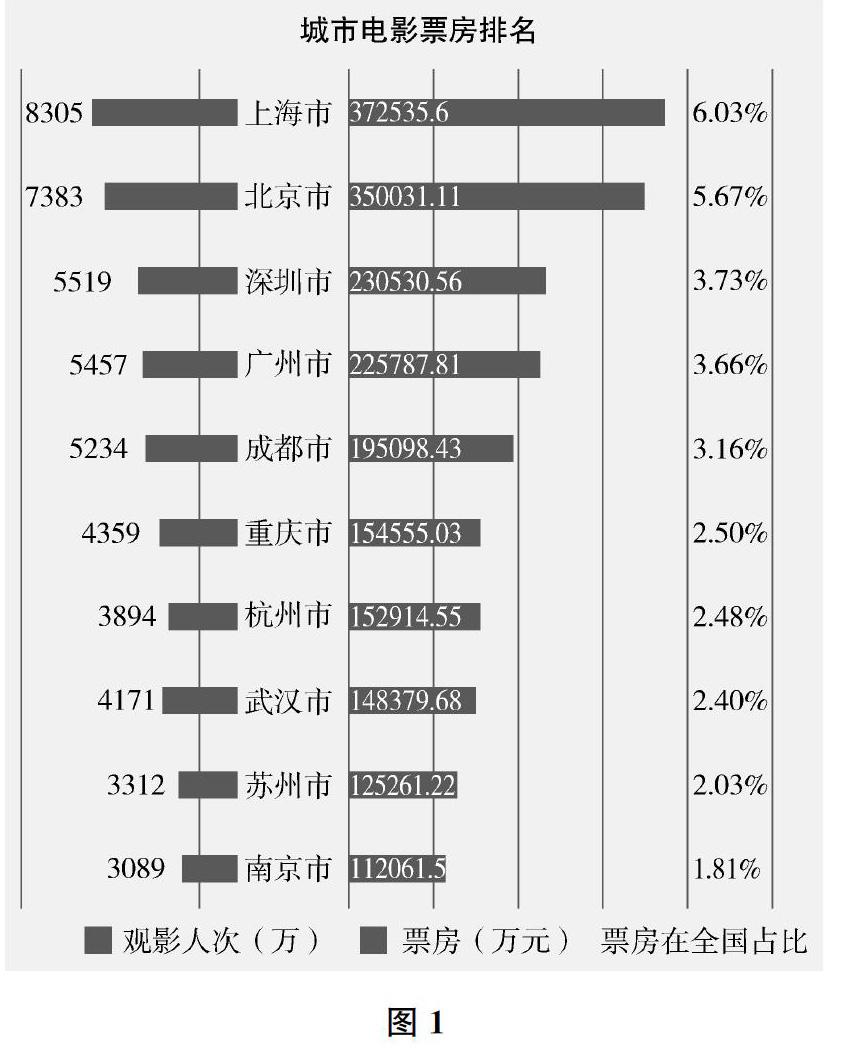
例2图1是经认证发布的2019年中国城市电影票房排名统计情况,请仔细阅读统计图,回答以下问题(可用计算器计算):
(1)2019年,苏州的电影票房收入比同省的南京要高,有人认为原因在于南京的电影票价比苏州低,但小明不同意这种说法。如果你是小明,你会怎样运用统计图中的数据说服他人?写出必要的算式。
(2)苏州、成都的平均电影票价大致相当,电影票房收入却有较大的差异,你觉得原因是什么?
(3)为提升苏州市的电影票房,请设计一句广告词,其中要含有数学元素,如百分数、方程等。
数据分析是当下大数据时代一种解释世界的方法,它不像传统数学那样依赖于计算效率与算术技能。例2便是如此,尽管需要运算,却不考查计算程序、笔算的精确度;更重要的是,计算结果不是问题解决的结论,而是数据分析的媒介。当学生列出195098.43÷5234<125261.22÷3312之类的式子时,运算在这里成了探索生活真理的方式。同时,学生在解这道题时,需要将内化的数学知识变成数学素养。例如,有学生在回答后两问时说:“除了人口因素以外,苏州的房价高于成都,所以成都人口袋里的钱就比苏州人多,自然有利于看电影这样的消费。”“苏州+电影=天堂里听故事。”……在千人千面的答题中,学生并未盲从数据,而是会用自己的数学思考涵养理性精神。甚至,学生还可以此题为基础,进一步做城市电影票房变量因素等的项目研究。
二、聚焦本质理解
命题时,应该聚焦对数学知识和方法的本质理解,而非形式记忆;同时,应该围绕数学内容主线,不以其他学科的知识、方法作为问题解决的主要依据。
例3(1)判断题:x=1是方程。()
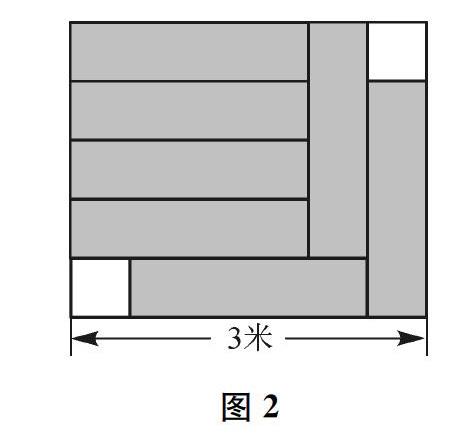
(2)如图2,为防止雨天路滑,环卫工人在一块长3米的长方形过道上铺了7张完全相同的长方形草席,请问:还有多少面积没有铺满?
许多版本的小学数学教材都这样给方程下定义:“像x+60=100、180=4x这样含有未知数的等式是方程。”但是,“这样的定义只是一种形式上的表述,不可能把握方程的本质”。史宁中教授指出:“方程描述的是现实世界中与数量有关的两个故事,其中用字母表示未知的量;这两个故事有一个共同点,在这个共同点上两个故事的数量相等。这是列方程的基本原则。”教学实践也一再表明,判断学生是否掌握了方程思想,“要去看学生列出来的方程左边、右边是不是都有意义并且描述简单”。
本题第1问中的“x=1”由于脱离了实际背景,不知道实际意义,无法判断是“数学故事”中的数量关系还是像“2x-x=x”一样的运算结果。这样直接考查概念的形式记忆,不利于概念的本质理解,会使学生钻入牛角尖,而忽视真正有价值的东西。
本题第2问就很好地考查了学生从图形中挖掘出隐含的数量关系(草席的长等于草席宽的4倍,草席的长加上草席宽的2倍等于过道的长),从而借助方程(也可运用算术方法)解决问题的能力,从而真正考查了学生对方程的本质理解。
例4妈妈买回5块饼分给兄弟2人,怎样分才合理呢?
本题的问题在于,学生可能会给出“弟弟比较小,所以弟弟分3个,哥哥分2个”“哥哥分2个,弟弟也分2个,剩1个给妈妈”这样的回答。这就导致将数学知识(平均分)的考查变成了思想道德(“孔融让梨”)的考查。
三、融入文化元素
数学是人类文化的发现与发明,不应脱离文化母体独立存在。历史上,很多人的很多事促进了数学的发展,给数学带来了新内容、新方法,这样的人和事便属于数学文化——数学名题、趣题也比比皆是。命题时,加入一点文化元素,将数学置于文化大系统中,看上去只是一份包装,实际上给学生带来了进行思维较量的冲动和数学冒险的信心,让学生从更宽广的视野审视数学的意义,从而格外注重用数学的眼光去丈量这个世界——毕竟数学在文化中总是扮演着智慧的角色。
例5于振善爷爷虽然是农民,但是非常爱动脑筋,曾用“称地图”的方法算出了一块地的面积,被称为“农民数学家”。现在,有一幅比例尺是1∶1000000的地图,长0.8米,宽0.5米。為求得图中某地域的面积,先把该地图贴在一块同样大小且质地均匀的木板上,称得整块木板质量为2千克,再沿待求区域的边缘将木板锯下,称得其质量为0.4千克。该地域的实际面积是多少平方千米?
这道题改编自农民数学家于振善的真实故事,只是将原故事中两、钱等旧式单位换成了常用单位。它让学生充分体验到数学的“善”,感受到数学的人文价值。
四、赋予分值多义
通常,命题工作还包括研制评分标准。评分时,对于整道题或某一步,除了答错不得分、答对得分这一基本评分标准之外,基于满意原则和加分原则,可以用不同的加缀数码标识相同的得分,赋予固定的分值多元意义,从而不仅关注答题结果的对错,也关注思维过程的优劣及差异。唯有淡化分值的量,而追究分值的质,才能够通过测评与学生的思考对话,厘清学生的问题或发现学生的才智,继而因材施教,以学定教。
例6(1)小明同学在学习中,和同学们一起探索发现:长方体的体积=长×宽×高=底面积×高;正方体的体积=棱长×棱长×棱长=底面积×高;圆柱的体积=底面积×高。于是,他猜想所有立体图形的体积都等于“底面积×高”。你觉得小明同学的猜想对吗?不管你认为对还是错,请给出你的理由。
(2)如图3所示是一个粮仓,顶部为圆锥形,主体为圆柱形,底面周长为18.84米,圆锥形的高和底面半径相等,圆柱形的高为10米。如果将这个粮仓改建成整体都是圆柱形,要求所容纳的粮食量不变,底面积也不变,那么改建后的粮仓高为多少米?(取π=3.14)
本题第1问,同样是答错不得分,回答为“小明同学的猜想是正确的,因为所有的立体图形都是用底面一层一层地铺出来的”,说明学生误认为所有立体图形上下一样粗;回答为“既然长方体、正方体、圆柱的体积可以这样计算,那么,别的立体图形的体积也都可以这样计算”,说明学生不理解不完全归纳推理的不确定性,不会用举反例的方法。评分时,可以在0后面加缀数码,予以区分错误的类型和水平。
本题第2问,同样是答对得分,可能有两种解法。(1)先求出底面半径为18.84÷3.14÷2=3(米),也是圆锥的高;接着求出粮仓的体积为3.14×32×10+13×3.14×32×3=282.6+28.26=310.86(立方米);最后用总体积除以底面积求出高为310.86÷(3.14×32)=11(米)。(2)只要将顶部圆锥改建为圆柱,且底面积和体积不变即可,那么只要将上面部分的高缩小为原来的三分之一;求出底面半径(也就是圆锥的高)为3米,可得缩小后上面部分的高为3÷3=1(米),于是,整体的高就是10+1=11(米)。第一种解法步骤多、计算量大,从中能看出学生思维严密,计算技能很强,但是只会套用公式,不能联结知识,变通思路;第二种解法步骤少、计算量小,从中能看到学生已经打通了知识联系,深刻领会到“等底、等高的圆锥体积是圆柱的三分之一”可以转化为“等底、等体积的圆柱高是圆锥的三分之一”,具有较高水平的逻辑推理素养。
参考文献:
[1] 史宁中.基本概念与运算法则——小学数学教学中的核心问题[M].北京:高等教育出版社,2013.
[2] 章勤琼.指向“建立方程模型”的“方程的意义”教学[J].小学数学教师,2018(11).
[3] 赵访熊.于振善尺算法的理论基础[J].科学通报,1951(11).3,12,22,24,75,77-79
