小学数学在线学习内容的“1+X”式拓展
2020-06-15姜华
姜华


摘要:“停课不停学”期间,微课在线学习成为重要的学习方式。但仔细分析微课在线学习,存在优秀学生“吃不饱”、基础薄弱的学生“吃不透”的问题。为满足不同学生的个性化和层次化需求,选择部分统一录制的微课作为基础,从趣味性、动态性、联系性和文化性等角度,对小学数学四年级在线学习内容进行“1+X”式拓展。
关键词:小学数学在线学习微课拓展
“停课不停学”期间,江苏省南京市建邺区教师发展中心组织优秀教师力量,录制了本学期各学科各年级教学内容的前30个课时的微课,以供本区教师在线教学时选用。笔者在学习了小学数学四年级的30个微课之后,发现了两个共性问题。
一是吃不饱。大部分微课教学内容较为浅显,以讲解教材中的例题和习题为主。这样托底式的安排,让优秀学生觉得“线上得来总觉浅”,存在在线学习“吃不饱”的问题。
二是吃不透。可能是微课教学时空的局限性,导致教师在难点的处理上常常采用“自问自答”和“掐头去尾烧中段”的教学方式,学生面对的只是一个个被教师平移过来却没有来由的方法和规则。刚性的方法和规则压缩了学生真实、自然、动态的学习进程。基础薄弱的学生只能死记硬背,难以自我内化,面临在线学习“吃不透”的问题。
笔者认为,如果只采用“拿来主义”,这样的纯微课在线学习很难满足学生个体的差异性和层次性需求。因此,教师需结合具体教学内容和学生学情,对在线学习内容进行拓展开发。由此,笔者对建邺区小学数学四年级在线学习内容进行了“1+X”式拓展——选择部分统一录制的微课作为基础(“1”),从趣味性、动态性、联系性和文化性等角度(“X”),对知识、技能、方法等学习内容进行拓展。
一、指向趣味性的拓展
据笔者统计,30个微课的学习内容中,有23个属于“数与代数”领域,涉及苏教版小学数学四年级下册《认识多位数》《三位数乘两位数》《用计算器计算》三个单元。这三个单元符号化的学习,让很多学生觉得数学无非是0—9这些阿拉伯数字的排列,平淡、枯燥,学习的热情也逐渐高开低走。但到了《用计算器计算》单元的第二课时《用计算器探索规律》,学生学习的热情却有了回升。在课后与学生的交流中,笔者明白了缘由:学习这样的内容时,学生不仅可以操作计算器,还可以了解很多有趣的规律,如142857这样的“走马灯数”。这也再次佐证了学习内容的趣味性可以很好地激发学生学习的积极性。
受此启发,笔者在《用计算器计算》单元末安排了一节拓展课《神奇的“缺8数”》,引领学生在观察、猜想、验证、质疑、推理等活动中探究“缺8数”(12345679)的奇妙性质:
(1)清一色:“缺8数”乘9的倍数(倍数小于10),结果会由同一个数字组成“清一色”;
(2)三胞胎:“缺8数”乘3的倍数(9的倍数除外),结果会由三个数字组成“三胞胎”(首位加0);
(3)轮流休息:“缺8数”乘不是3的倍数的数,结果的各位数字均不相同。
学生在探究中感受到“缺8数”的神奇之处和数学的规律之美。“缺8数”的拓展好似星星之火,点燃了学生探究的热情。他们兴奋地借助网络查阅资料,认识了更多神奇的数:回文数、三角形数、金字塔中的数、数字黑洞495……神奇的“缺8数”好似一根线,串起了一颗颗闪亮的“数字珍珠”。学生在这样的串联中感受到数字的结构美和对称美。数字在他们眼里少了一份平淡和枯燥,多了一份神奇和趣味;少了一份冰冷,多了一份热情。
美国科普大师马丁·加德纳指出,唤醒学生的最好办法是向其提供有吸引力的数学游戏、智力题、魔术、笑话、悖论、打油诗或那些呆板的教师认为无意义而避开的其他东西。因此,我们应想方设法拓展在线学习内容的趣味性,让学生在学中生智,练中生趣,感悟数学的魅力,从而产生浓厚的学习兴趣。
二、指向动态性的拓展
数学学习应是一个生动活泼的过程,数学教学应是将教材中静态的知识转化成学生动态学习的过程。受教学时空的限制,微课中只能将需要学生动手操作的内容通过动画演示出来,学生常常会出现不操作或操作体悟不完整的现象,导致他们的空间想象无法启动或深入。因此,在线教学应为学生提供尽可能多的操作和实践的机会,让动作为思维服务。
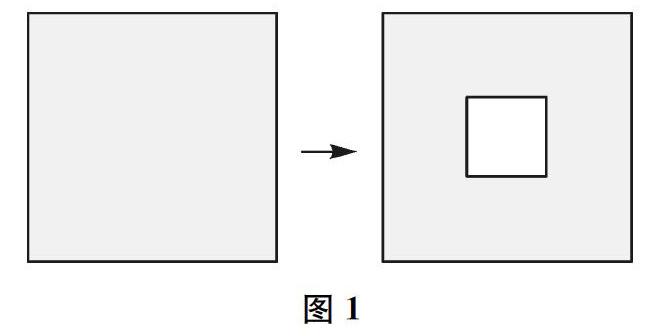
例如,《平移、旋转和轴对称》一课,笔者基于“轴对称图形”知识进行了“剪纸成图”的动态性拓展,让学生在一张正方形纸上剪下一个小正方形(如圖1所示)。
学生在动手操作的过程中,发现将正方形先对折,剪起来比较方便,不同的对折次数,剪法也不一样。而实际操作的过程并不那么顺利,“对折之后再剪哪里?”“剪掉一个什么样的图形?”都是需要考虑的问题。因此,在操作过程中,学生也收获了很多“意外”(见图2)。这些“意外”为学生操作经验的积累和空间想象的发展提供了依托。
“儿童的智慧就在他们的手指尖上。”对学习内容进行动态性拓展,不仅有利于调动学生学习的积极性,而且有助于学生积累数学活动经验,发生数学深度学习。
三、指向联系性的拓展
对学生而言,难题通常难在其丰富的变式及其难以触及的生长根源。一些学生面对难题时常常望而却步,只能死记硬背一些方法和规则,难题在他们眼里是那么的“高冷”。若能带着学生找到难题生长的根源,循着一次次的变式拾级而上,难题也会变得“平易近人”。
例如,对于《三位数乘两位数》单元的一道思考题(见图3),微课以1分16秒的时长程序化地告知学生:要使乘积最大,先选4个较大的数字组成乘积最大的两位数乘两位数,再将最后一个数搭配进去,比较出计算结果;要使乘积最小,先选4个较小的数字组成乘积最小的两位数乘两位数,再将最后一个数搭配进去,比较出计算结果。很多学生初见这样的思路,不明就里,找不到此题生长的根——三年级学习“两位数乘两位数”时曾练习过用给定的4个数字组成乘积最大或最小的两位数乘两位数,近一年的时间跨度导致很多学生对此已经有所淡忘。
基于题目的难度和学生学情,笔者将这道思考题设计成两节拓展课——《哪道算式的乘积最大》和《哪道算式的乘积最小》,聚焦知识生长的顺序进行了纵向和横向的联系性拓展。下面以《哪道算式的乘积最大》为例具体说明。
纵向联系。首先,组织学生在猜想、验证中探究4个数字(非0)组成的两位数乘两位数的乘积最大的组合方法。学生的前数学经验逐渐得到重启和激活。在此基础上,再次引导学生通过猜想和验证,探究5个数字(非0)组成的三位数乘两位数的乘积最大的组合方法。学生刚刚获得的“如何將4个数字(非0)组成乘积最大的两位数乘两位数”的经验得到了进一步的提升。学生在这样的纵向联系中,触及知识的脉络,体悟到知识发展的“序”。
横向联系。在分别用4个数字和5个数字组成符合要求的乘法算式的环节,学生都需要对每次组成的两道算式的结果进行比较。这时,竖式验证是一种方式,还可以根据实际情况巧比。笔者就“巧比”进行了两次横向联系。第一次,先运用数形结合的方式,启发学生联系三年级所学的“周长与面积的关系”,让学生知道“当周长一定时,长方形的长和宽越接近,面积就越大”。继而,学生也就明白了在比较“42×31”和“41×32”的结果时,也可以运用类似的方法。这一横向联系,让学生“形”的经验在“数”的学习中有了落脚点,真正实现了数与形的结合。 第二次,在比较类似“52×431”和“521×43”的算式的结果时,引导学生根据乘法的意义拆分算式:52×431=52×430+52×1,521×43=52×430+43×1。即从乘法分配率的角度实现巧比。这一横向联系,调动了学生最本源的学习经验,也为后续乘法分配律的学习做了孕伏。
非0数字组合的算式已经理解透彻了,含0算式的探究就轻而易举了;内化了最大积的寻找方法,最小积的寻找方法就可以自然生长了。拓展在线学习内容的联系性,可以帮助学生摸清知识脉络,真正建构起属于自己的知识结构。
四、指向文化性的拓展
本次的微课学习内容,有4个涉及教材中的《你知道吗》栏目,均只是对数学文化的简单介绍;而其他的都没有涉及数学文化的拓展。可见,这次的微课并没有将数学文化自然地渗透在教学内容中,数学文化与教学内容依旧是“两张皮”。由此,学生也只能听听看看,偶尔发出一些感叹,依旧难以体会到数学知识的文化性,不利于其情感态度和价值观的发展。对此,笔者采用以下两种方式来拓展学习内容的文化性。
(一)扩容教材中的文化介绍
《用计算器计算》单元的第二个《你知道吗》栏目,教材以简短的语句介绍了筹算、珠算、计算机,意在让学生体会计算工具演变和发展的大致历程,感受古代劳动人民和数学家的智慧,以及计算工具的演变和发展对社会文明的促进作用。本次制作的微课,在临近结束的30秒左右对这些内容进行了介绍。这只是教材的有声平移,难以引发学生深刻的感悟。
笔者在整合教材的基础上,以“计算器的历史”为题,开展了文化拓展。以“你知道最原始的计数工具是什么吗?你知道世界上第一个计算器是什么样子的吗?”为引子,一下子激发了学生的好奇心,抓住了学生的兴奋点。在一幅幅图片中,学生仿佛打开了一幅源远流长的数学画卷,回到了远古时代,知道了石子、结绳、木棒、手指、刻痕等都是人类最初用来计数和计算的工具,理解了人类在劳动中建立起来的“一一对应”的计数方法。徜徉在数学发展的历史长河里,学生知道了:早在2500多年前的春秋战国时期,人们就已经普遍使用算筹来计数了,表示数的算筹有纵、横两种方式;继算筹计数之后,算盘是我国古代劳动人民发明的又一个更简便的计算工具;1642年,法国科学家帕斯卡根据算盘的原理,发明了第一部只能计算加减的机械式计算器;1694年,德国数学家莱布尼茨对机械式计算器做了改进,才有了还可以计算乘除的计算器;直到20世纪50年代末,电子计算器才出现。在计算工具逐渐演变的历史画卷里,学生惊叹于古代劳动人民和数学家的智慧和创造,更是触摸到了数学的历史和力量。
(二)增添教材外的文化链接
《三位数乘两位数》单元的教学基础是,学生已经熟练掌握两、三位数乘一位数和两位数乘两位数。根据以往的教学经验,绝大部分学生可以自主通过类比解决新的计算问题。因此,微课中仅以教材例题为依托,在具体细致地演示了竖式计算的过程之后,以一些常见的练习收尾。但是,本单元是苏教版小学数学教材整数乘法教学的最后一个单元,如何让学生在此浅显处学得更深入呢?
受“两位数乘两位数”教学中“铺地锦乘法”的启发,笔者在本单元教学中拓展了印度的“画线乘法”。学生在观察、运算中兴趣盎然地掌握了画线乘法的算法,体会到画线乘法的直观性和算法的多样性。同时,笔者还引导学生将画线乘法和竖式乘法进行对比,沟通联系(如图4所示),帮助学生在厘清关系的同时进一步理解算理,发展数感。学生也在对比中发现了画线乘法的弊端,体会到竖式乘法的简便性。
数学是一种文化,数学学习是一个有生命力的过程。在线数学学习不应只是知识和方法的简单汇聚,还应是一个开放的文化平台,向学生展示人类智慧和创造力的结晶,帮助学生拔节数学思维,拓宽数学视野。
参考文献:
[1] 潘小福.小学数学教材的专业化解读[M].南京:江苏凤凰教育出版社,2017.
[2] 陈加仓.小学数学拓展课:教什么,怎么教[M].北京:中国人民大学出版社,2017.
[3] 谷尚品.小学数学拓展课案例精选3[M].杭州:浙江教育出版社,2019.
[4] 洪细苗.小学数学拓展课案例精选4[M].杭州:浙江教育出版社,2019.
