双渠道定价与库存联合决策和协调机制选择

王 敏 李富昌

(云南师范大学 云南 昆明 650500)

一、问题描述与模型

在传统零售中，批发价格的谈判多以制造商为领导，零售商的议价能力比较弱；双渠道的视角中，批发价格谈判不再由制造商单独决定，零售商业参与议价，作为零售价格与直销价格在分散决策时处于平等地位。

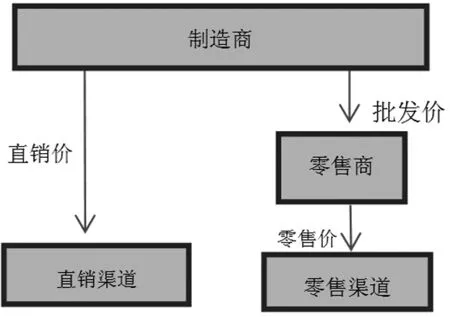
图1 双渠道定价联合决策协调机制

建设一个双渠道供应链，分为制造商和零售商，商品的生产由制造商负责，并将商品通过线下零售渠道和线上渠道进行销售。假设1代表线上渠道，2代表线下渠道，制造商的单位生产成本为c，批发价格为l，零售价格为p，直销价格为d，单位产品在线上渠道成本为k(k>0)，零售商的固定成本为C(包含实体店铺和运输成本)，线上渠道销售占市场总份额的比率为m，商品市场需求为x，消费者对价格的敏感系数为y，利润为P。所以，制造商线上渠道和零售商线上线下渠道的需求函数是：

f1=mx-yp1

(1)

f2=(1-m)x-yp2

(2)

本文主要研究零售商在线上线下销售中的主要占比，所以计算出制造商收益、零售商收益和供应链总收益：

P1=(l-c)(f1+f2)+f1(d-c)=(l-c)(x-yp1-yp2)+df1-cf1

(3)

P2=(kp1-l)f1+(p2-l)f2-C

(4)

P=P1+P2=(kp1-2c+d)f1+(p2-c)f2-C

(5)

当双渠道供应链联合机制选择时，可产生最优决策。在这样的优化策略中，供应链总收益总表达式是式(5)。对式(5)求p1和p2的二阶偏导数，可得到目标收益关于p1和p2的Hessian 矩阵为：

(6)

由上可得，目标函数存在唯一解。令式(5)关于p1和p2的一阶偏导数等于0，回代求解，得到各项均衡解：

(7)

(8)

得出联合决策下总供应链的最优利润是：

(9)

由式(9)可以证明，在集中式决策情形下，供应链整体收益与k正相关，说明制造商和零售商耗用在线上渠道费用较高，对总供应链的利润造成负担，所以在双渠道联合决策问题上的成本对k的研究应该重点分析，在收益共享契约中达到定价协调策略。

二、基于收益共享契约的定价协调机制选择决策

建设Stackelberg博弈模型，由于零售商控制双渠道的总市场，那么其先确定线上和线下的销售价格，采用逆向归纳法求解，函数表达式为：

l=p1-l1=p2-l2

(10)

第一点求的是制造商确定自己获得最大利益的价格阶段，这个时候制造商的策略函数是：

P1=(l-c)(x-yp1-yp2)=(l-c)(x-(2l+l1+l2)y)

(11)

对l求一阶导数并令其等于0，可得到制造商最优价格决策：

(12)

对l求二阶导数，存在-4y<0，此时的最优批发价格l*使得制造商的利润获得最大值。

(13)

对式(4)分别求p1和p2的二阶偏导数，可得到目标收益关于p1和p2的Hessian矩阵是：

(14)

得到制造商在批发价格契约模型下的最优策略：

(15)

由式(15)可知，最优批发价格l*=与参数k正相关。可得到双方最优决策下的总利润是：

(16)

三、算例分析

通过理论分析发现渠道成本k对双渠道供应链定价产生重要影响，为了从实证角度进一步证实理论分析的合理性，以及验证k对其他参数的影响程度，下文通过数值算例对理论模型进行检验。假定市场总需求x=100，消费者对价格的敏感系数y=10。

(1)k和m对p1和p2的影响

从表 1 可以看出，线上零售价格p1随着渠道成本k的降低而逐渐增加，无论是制造商为供应链主导者模型下还是零售商为供应链主导者模型下，传统渠道销售价格高于直销渠道销售价格，对于传统零售商来说，直销渠道可以节约大量的运输成本和营销成本，同时可以减少运输时间，一定程度上传统零售商消耗的成本较大。

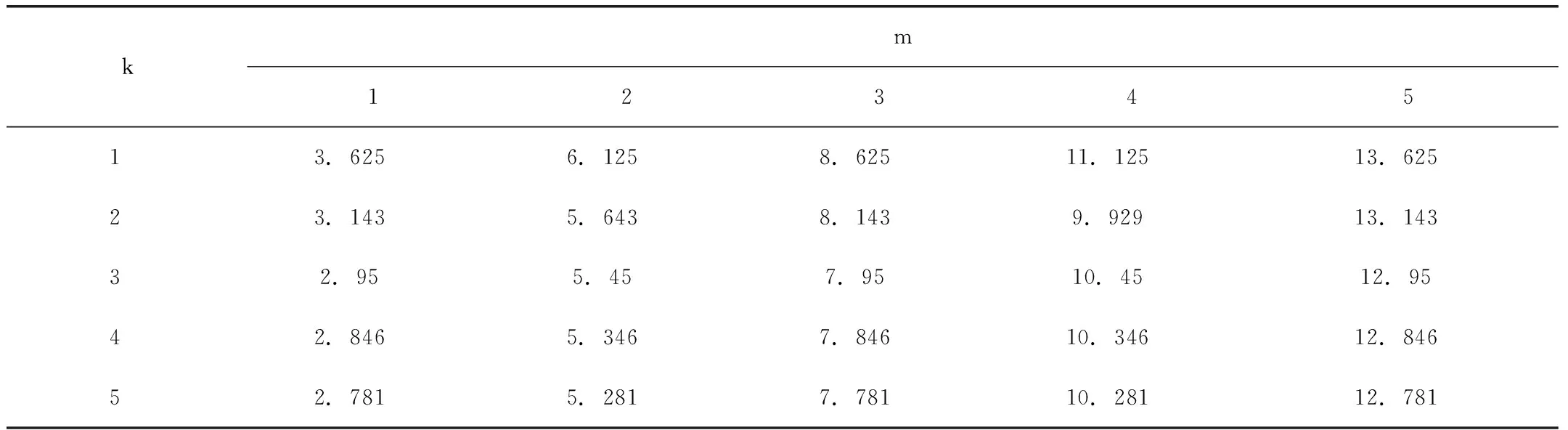
表1 k和m 对p1的影响

(2)渠道成本k对批发价格的波动情况

从图2可以看出，随着渠道成本k的提高，最优批发价格l也在升高，说明当渠道成本增加时，制造商也会通过增加批发价格来缓解成本压力。

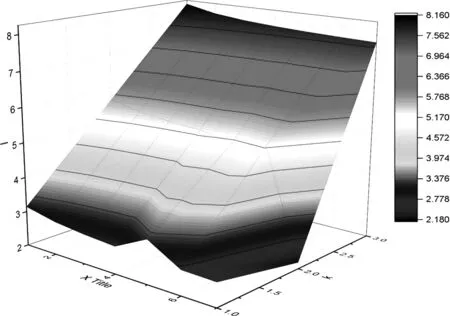
图2 渠道成本k对最优批发价格l的影响

四、结论

本文得出：在集中式决策情形下，供应链整体利润与k正相关，线上收取的技术服务费费率越低，供应链整体利润就越高；最优批发价与参数k 正相关；价格p1随着的k增加而降低，随着m的增加而升高；传统渠道销售价格与产品批发价格会随着直销渠道的增加而降低。制造商为供应链主导者结构下的批发价格与传统渠道销售价格，高于零售商为供应链主导者结构下的情况。因此，无论是零售商利润还是制造商利润，在其为供应链主导者时最大。供应链总利润在零售商为供应链主导者时最优。本文探讨了在单一制造商与单一零售商组成的双渠道供应链结构下，最终实现基于收益共享契约下动态联合优化策略。