浙江省毛竹竹秆材积模型*

2020-06-15沈钱勇汤孟平

林业科学 2020年5期

沈钱勇汤孟平

(浙江农林大学环境与资源学院省部共建亚热带森林培育国家重点实验室杭州 311300)

毛竹(Phyllostachysedulis)是我国南方重要的森林资源之一，在增加经济效益、发挥生态服务功能等方面具有积极作用(周国模等， 2004；杨麒麟等， 2017)。浙江省是我国毛竹主产区，根据2016年浙江省森林资源与生态状况年度监测，全省森林面积605.91万hm2，森林蓄积31 529.17万m3，其中毛竹林面积80.71万hm2，占森林面积的13.32%，毛竹林每公顷立竹量3 413株。森林蓄积是当前评价森林生产力和林木生长状况的重要指标(唐守正等， 2000；孟宪宇， 2006)，对毛竹林蓄积仅采用每公顷立竹量表示是不精确的，在我国木质资源短缺、倡导以竹代木的发展趋势下，通过单株毛竹材积测定从而准确估算毛竹材积具有重要意义。

目前，国内外对立木材积的估算方法主要有2种(刘镜婷等， 2016)：一是采用线性或非线性回归拟合一元或二元材积模型(Snorrasonetal.， 2006； Caseetal.， 2008)；二是利用二元材积方程和树高曲线方程构建含误差变量的相容性联立方程组模型进行参数估计(胥辉，1999； Tangetal.， 2001； 2002；曾鸣等， 2013)。毛竹竹秆中空、尖削度大，其材积计算不能简单地套用立木材积方程(陈双林等， 2008)。20世纪50年代，虞岳世等(1958)研究毛竹材积与胸径、竹高的关系，采用竹秆分段测量壁厚方法测定竹壁材积，建立了一元(胸径)和二元(胸径、竹高)材积模型；此后，吴丁(1987)、张振瀛等(1990)也采用类似方法分别建立了一元和二元材积模型。然而，以往建立的材积模型都忽视了竹隔材积，为此，张刚华等(2007)改进测量方法，除分段测量直径、壁厚外还测量每个竹隔厚度，并建立了包含竹隔在内的一元竹秆材积模型。

应当指出，现有毛竹竹秆材积模型均未充分考虑毛竹的竹节、竹壁和竹隔的形状不规则性，不能准确测量竹秆材积，建立的竹秆材积模型不够精确。而且，毛竹竹杆弯曲生长特性以及冠层枝叶遮挡对竹高的准确测量也有较大影响，造成基于竹高所建立的材积模型存在应用的局限性。鉴于此，本研究以浙江省毛竹林为研究对象，采用可测量不规则物体体积的排水法准确测量竹秆材积，引入胸径、竹高和胸高节长因子，通过初步筛选选择5个材积模型进行比较研究，并通过模型误差结构及模型拟合优度和预估精度的评价分析，确定适用于浙江省的毛竹竹秆材积模型，以期为毛竹林经营管理提供依据。

1 材料与方法

1.1 数据来源

2016年7月至2018年7月，在浙江临安、庆元、武义、常山、宁海、安吉、诸暨、余姚、黄岩和泰顺10个县(区、市)，选择近年未受人为经营管理的毛竹林，随机选取梢头完整、竹秆通直、断面近似圆形、无破损和病虫害的样竹216株，测量胸径、竹高和胸高竹节长(图1)。样竹株数径阶分布如图2所示，经检验，样竹株数按径阶呈正态分布(P<0.01)。

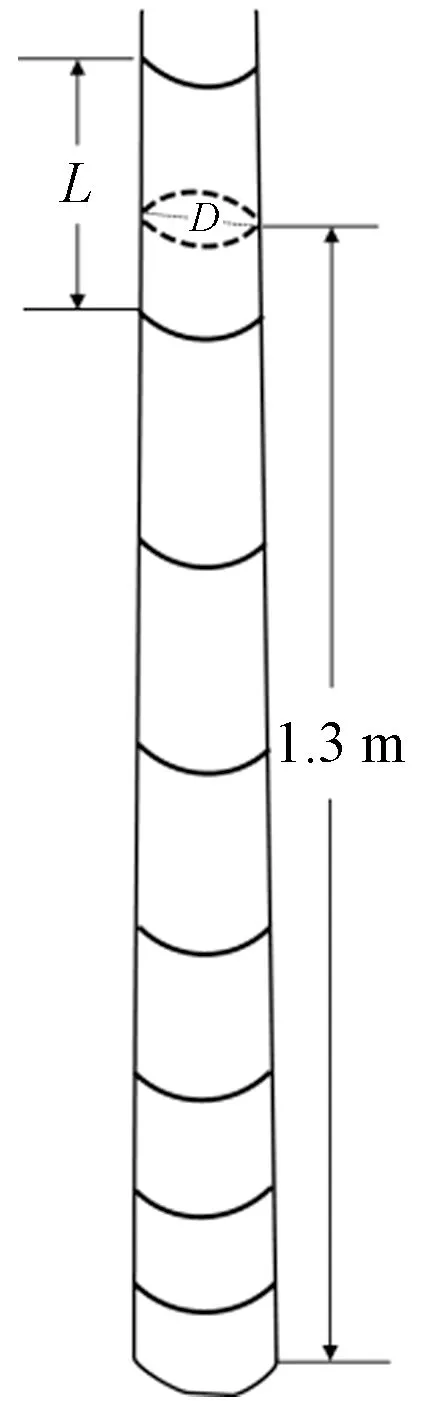
图1 毛竹竹秆材积建模变量示意

伐倒样竹，采用排水法测定竹秆材积。首先，将水注入定制水桶内至水龙头齐平处，排出桶内多余的水；然后，将竹秆分成竹条放入水桶内，用电子提秤称量通过水龙头排出的水量；最后，计算毛竹竹秆材积。公式如下：

(1)

式中：Vs为竹秆材积(dm3)；Mw为排水质量(kg)；ρ为水的密度(1 g·cm-3)。

样竹按胸径(D)、竹高(H)、胸高节长(L)和竹秆材积(V)等主要指标统计情况如表1所示。可见，竹秆材积的变异系数最大，胸高节长的变异系数最小。

图2 样竹径阶分布

表1 毛竹样竹实测数据统计

1.2 毛竹竹秆材积模型研建

1.2.1 竹秆材积模型选择立木材积方程一般包括4类，即组合变量方程、对数材积方程、Horner材积方程和广义材积方程。通过初步筛选和比较，本研究基于广义材积方程，选择幂函数形式的一元模型及山本式和寺崎渡方程的4个二元模型进行分析比较。一元模型基于以胸径为自变量的式(2)，二元模型基于以胸径、竹高和胸高节长为自变量的式(3)～(6)(孟宪宇， 2006)，5个毛竹竹秆材积方程为：

M1：V=a0Da1；

(2)

M2：V=a0Da1Ha2；

(3)

M3：V=a0Da1La2；

(4)

M4：V=a0Da1ea2/H；

(5)

M5：V=a0Da1ea2/L。

(6)

式中：V为竹秆材积(dm3)；D为胸径(cm)；H为竹高(m)；L为胸高节长(cm)；ai为模型参数，i=0、1、2。

基于以上5个材积方程建立模型需考虑误差项，有加性和乘性之分。对于含乘性误差项的模型，利用对数回归进行参数估计后需要转化成原始结构，且需对误差项进行修正(Baskerville, 1974；曾伟生等， 2011a)。

在对数回归模型研究中,学者们提出过许多校正因子(Finney，1941； Baskerville，1974； Snowdon，1991)，其中以Baskerville(1974)提出的校正因子[CF=exp(s2/2)](s为回归估计标准差)应用最多。曾伟生等(2011b)则基于对数转换特点提出了新的校正因子[CF=(1+s2/2)]。通过比较发现，采用不同校正因子修正后的模型各项评价指标并无差异(Dongetal.， 2014)，本研究选择的校正因子为CF=(1+s2/2)。预估材积模型如下：

(7)

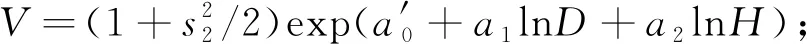
(8)

(9)

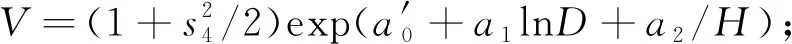
(10)

(11)

1.2.2 毛竹竹秆材积模型误差结构分析采用似然函数法，分析基于5个不同方程的毛竹竹秆材积模型误差结构(Xiaoetal.， 2011； Dongetal.， 2014；董利虎等， 2016)，确定应当采用对数回归或非线性回归模型进行模型拟合。具体计算步骤如下：

第1步：利用原始数据分别进行对数线性回归和非线性回归拟合，得到5个模型的参数估计值(ai)和方差(σ2)。计算5个模型各自的对数似然值(lnL)，通过下式计算各模型的赤池信息量准则(AICc)：

(12)

式中：k为模型参数个数；n为建模样本数量； lnL为模型的对数似然值。

对数转换线性回归模型的赤池信息量准则称为AICcln，非线性回归模型的赤池信息量准则称为AICcnorm。

第2步：分别对比5个模型的2个赤池信息量准则，若ΔAICc(AICcnorm-AICcln)<-2，表明模型误差项是相加的，应基于原始数据进行非线性回归拟合；如果ΔAICc> 2，则说明模型误差项是相乘的，应进行对数转换的线性回归拟合。

1.2.3 模型评价与检验模型拟合优度和预估精度通过以下4个指标进行评价检验：

调整确定系数

(13)

(14)

(15)

(16)

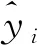
2 结果与分析

2.1 竹秆材积模型误差结构分析

分别利用原始数据的非线性回归和对数转换的线性回归拟合5个基础材积模型[式(2)～(6)]，求得各模型的赤池信息量准则(AICcnorm和AICcln)，相比较得到5个模型对应的ΔAICc(表2)。

表2 浙江省毛竹竹秆材积模型误差结构似然分析统计

由表2可知，通过对数转换线性回归拟合的模型与利用原始数据直接拟合的非线性模型获得的AICc相比，5个模型的ΔAICc均大于2，说明本研究浙江省毛竹竹秆材积模型误差结构为乘积型误差，5个模型都应当采用对数转换的线性回归进行拟合分析。

2.2 竹秆材积模型拟合与评价检验

不分建模样本和检验样本而利用全部样本建立材积模型，能充分利用其信息，可得到预估误差最小的模型(Myers，1986； Kozaketal.， 2003；曾伟生等， 2011c；唐思嘉， 2017)。本研究利用全部样本，采用对数转换的线性回归进行竹秆材积模型拟合分析，并通过拟合优度和预估精度指标对模型进行评价和检验。

比较各模型的统计指标结果，模型M2最优，其次是M5。从便于实际应用角度，确定采用包含胸径和胸高节长的毛竹竹秆材积模型M5。

表3 竹秆材积对数回归模型拟合参数与统计指标①

①括号内数值为各参数t检验值。Values in bracket arettest value for each parameter.

从对数回归模型残差分布(图3)也可看出，各模型残差随着预测值增大基本呈均匀分布，不存在异方差。

以上检验是基于全部样竹的平均值，并不能很好反映出不同大小(胸径)毛竹竹秆材积的预估情况(Kozaketal.， 2003)。因此，本研究对5个对数回归模型各径阶的平均偏差进行检验(图4)。可见，5个模型的预估偏差随径阶并未发生明显的变化，均接近于0。从数值上看，各模型在4.0～5.9 cm和14.0～15.9 cm径阶时，偏差相比较其他径阶大，其中前者略有低估，后者略有高估。由图4也可看出，各模型在不同径阶范围的预估精度均较高。

图3 竹秆材积对数回归模型残差分布

图4 不同径阶竹秆材积对数模型平均偏差检验

2.3 对数模型校正

基于对数转换的线性回归模型预测的是期望材积对数值，而要获得材积实际值(即算术尺度下的材积预估值)，则需要对对数模型预测值进行反对数转换(Dongetal.， 2014)。一般认为，反对数转换过程中会对材积等预测值产生系统上的低估，因此需要对其进行校正(Finney，1941； Baskerville，1974； Packardetal.， 2008； Cliffordetal.， 2013)。

表4所示为5个模型反对数转换后的部分统计指标。可以看出，对对数模型进行校正后，模型拟合优度和预估精度变化不显著。Madgwick等(1975)研究指出，反对数转换引入校正因子会高估预测值，认为当对数模型误差项足够小时，反对数转换过程中无需进行校正； Dong等(2014)比较不同校正因子进行反对数转换模型校正与不做校正的模型统计指标，也发现同样规律。根据表4，利用本研究得到的对数模型进行反对数转换得到材积预估值，从ME和MSE可以看出，模型本身具有较高的拟合优度和预估性能，误差较小；而通过校正后，则会高估预测值，平均偏差和平均系统误差均明显增大。

表4 对数模型反对数转换在原始尺度下的非线性模型校正评价检验①

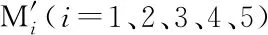
3 讨论

常用的生物模型如材积模型，一般采用幂函数等非线性函数的对数回归拟合或直接非线性拟合的方法获得相应模型(Parresol， 2001； Zianisetal.， 2011； Dongetal.， 2014)，而对于采用何种方法进行模型拟合能获得最佳效果依然存在争论。近年来，林业和生态研究领域的一些学者也开始利用似然函数法对林木生物量等模型的误差结构进行分析，以确定应采用何种建模方式进行建模(Xiaoetal.， 2011； Ballantyne， 2013； Laietal.， 2013； Dongetal.， 2014；董利虎等， 2016)。

Dong等(2014)为了说明不同误差结构对模型拟合精度的影响，对落叶松根部生物量数据同时进行了基于幂函数形式的对数回归模型和非线性模型的研建，为保证比较模型具有相同的响应变量，其针对2种形式模型分别进行了原始尺度下的反对数转换和对数转换尺度下的对数转换，即LR模型由线性回归直接拟合，NLR*模型的相关统计指标基于直接非线性拟合的NLR模型预测值进行对数转换重新计算获取，利用对数尺度下的数据进行预测评价检验；而在原始尺度下，NLR模型直接利用原始数据非线性拟合，LR*模型的相关统计指标则基于LR模型预测值进行反对数转换重新计算获取，利用的是算术尺度数据。本研究比较了2种尺度下模型M5各径阶的平均百分标准偏差(MPSE，%)，计算公式见参考文献(曾伟生等， 2011)，结果如图5所示。可以看出，在原始尺度下，NLR模型和LR*模型各径阶预估精度变化较小，分别在4.0～5.9 cm径阶和12.0～13.9 cm径阶时最高。在径阶4.0～9.9 cm之间，LR*模型的MPSE均小于NLR模型，但径阶大于10 cm时，2种模型精度值接近(图5A)；而在对数转换尺度下，2种模型预估精度均呈随径阶增大而升高的趋势，且LR模型的MPSE在各径阶基本低于或接近NLR*模型(图5B)。不难看出，当模型误差结构为乘积型时(对数尺度下)，利用对数转换线性模型具有更佳的预估效果，偏差较小。

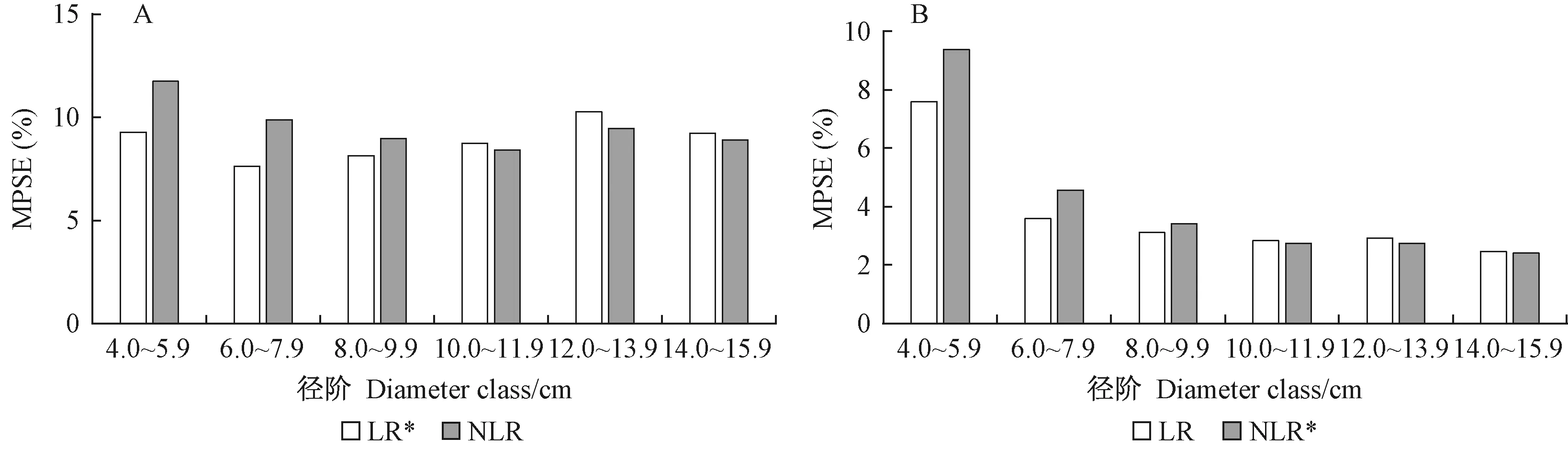
图5 原始尺度(A)和对数转换尺度(B)下线性模型和非线性模型各径阶的平均百分标准偏差

通过不同径阶竹秆材积对数模型平均偏差检验结果(图4)与不同尺度下线性模型和非线性模型预估精度(图5)的比较可以发现，各模型对于不同径阶毛竹竹秆材积的预估效果均较好，差异不大。但应看到，在最小径阶时，模型预估精度易出现波动(图5B)，这或许与该径阶样本数据较少有关(4.0～5.9 cm径阶仅有12株)，后续应对大径阶和小径阶毛竹开展更多研究。

许多关于对数回归模型的研究均提出需对模型进行校正以减少或消除偏差的影响。本研究对比5个对数模型进行反对数转换校正和未经校正的统计指标(表4)发现，对数模型拟合优度较高、预估误差较小，进行反对数转换校正后，会高估材积值，与Madgwick等(1975)的研究结果一致。故本研究在进行对数模型反对数转换时未进行校正。

与二元材积模型相比，一元模型的拟合优度和各径阶偏差等并无显著差异(表3、图4)，亦能满足单株材积或单位面积竹林蓄积预估的精度要求，在生产上具有简便和实用性；但引入胸高节长和竹高变量后，所建立的二元竹秆材积模型具有更高的拟合优度。在实践中，由于胸高节长较竹高更易准确测量，因此包含胸高节长变量的毛竹材积或生物量模型具有进一步研究的应用价值；同时，有必要在更大范围进行数据调查，提高模型精度，增强模型的适用性，并推广应用于我国毛竹林经营实践。