采用硅流体芯片的气动位置控制系统特性研究

吴央芳， 周铖杰， 夏春林， 王玉翰， 陆倩倩

(1.浙江大学城市学院机械电子工程系， 浙江杭州 310015； 2.常州大学机械工程学院， 江苏常州 213164)

引言

气动控制系统以压缩空气作为动力源，在制造[1-2]、自动化[3-4]、机器人[5-7]等工业领域中有着广泛的应用。与液压控制系统相比，气动系统具有清洁无污染、无火灾隐患、安装方便等优点，受到了广泛的关注。李晨景等[7]对一种新型气动爬杆机器人进行了建模及仿真研究提升了机器人的性能。刘洁等[8]对采用PMDS驱动的气动微型阀进行了研究， 并将其应用在了新型智能痕量灌溉系统中。ZHONG等[9]将4个开关阀作为气动控制元件，利用改进的滑模控制算法减小了控制系统的超调，提高了系统的响应速度。NAZARI等[10]利用FESTO公司的MPYE型比例方向阀搭建了气动位置控制系统，并采用改进的模糊控制算法进行了实验研究，结果表明系统对较低频率(0.5 Hz)的正弦信号具有较好的跟踪能力。气动控制阀作为流体流动与电子控制的接口，是气动控制系统中的关键部件之一。硅流体芯片[11](Silicon Valve，也称硅阀)，是一种基于MEMS(Micro-Electro-Mechanical System，微机电系统)技术的热致动微型阀。早在1999年，WILLIAMS等[12]设计了最初版本的硅流体芯片，并进行了实验测试，结果表明所设计的硅流体芯片具有良好的特性，在低压(0.1 MPa)的情况下，芯片的泄漏小，随着压力的增大，泄漏和滞回会逐渐增大，芯片的最大可控制压力达1.4 MPa。李勇俊等[13]对芯片的致动器进行了优化设计，采用变截面的设计改善了致动器结构的温度分布，提高了芯片的综合性能。SKIMA等[14]提出了一种微机电系统的混合预测方法，并对芯片进行了疲劳测试，通过实验验证了预测方法的准确性。

硅流体芯片具有尺寸小(10.8 mm×4.8 mm×2.2 mm)、易于集成、控制精度高的特点，是工业供热通风与空气调节领域的研究热点[15]，但在气动控制领域的应用研究还相对较少。将其作为气动比例压力阀应用于气动位置控制系统中，通过实验及仿真的方式探究系统的输入输出特性，对将来提高采用硅流体芯片的气动位置控制系统精度及实现缸阀一体化、小型化具有一定意义。

1 硅流体芯片的工作原理

硅流体芯片的结构如图1所示，采用片式的结构设计，中间层带有V形电热微致动器和杠杆机构。当芯片通入控制电压时，由于欧姆热效应电流经过V形电热微致动器会使筋的温度升高，导致热膨胀，产生沿 A方向的位移，B点则作为杠杆机构的支点将位移放大，以改变ps,po口的过流面积大小，达到比例调节输出压力或流量的目的。芯片的等效工作原理图如图2所示，可看成是一个具有可调孔的半桥。

课题组前期已对芯片进行了初步的仿真、实验及应用研究，基于硅流体芯片设计了两种不同结构(单/双芯片结构)的气动比例压力阀，实验结果表明这2种结构的比例阀都具有良好的性能。其中双芯片结构的比例阀实物及结构简图分别如图3、图4所示，主要由2个芯片并联组合封装在带有控制腔的模块中构成。

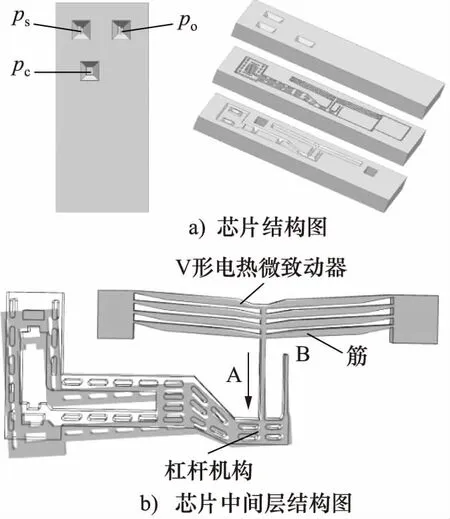
图1 硅流体芯片结构图

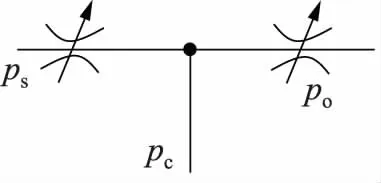
图2 芯片等效原理图

图3 双芯片结构比例阀实物图

图4 双芯片结构比例阀结构简图

2 数学建模

采用硅流体芯片的气动控制系统气路及气缸活塞杆受力分析简图如图5所示。

假设气路中工作的气体为理想气体，气体通过硅流体芯片阀口的质量流量计算公式如下[16-17]：

(1)

式中,pin—— 芯片阀口输入压力

pout—— 芯片阀口的输出压力

Cd—— 流量系数

A—— 过流面积

T—— 临界温度

γ—— 比热

R —— 理想气体常数

pcr—— 临界压力比

pc—— 压力比

图5 系统气路及气缸活塞杆受力分析简图

其计算公式如下：

(2)

根据理想气体的状态方程[18]，有：

paVa=maRTa

(3)

式中，pa—— 气缸腔室A中气体的压力

Ta—— 温度

Va—— 体积

ma—— 质量

假设流体流动的过程绝热，且腔室中流体的温度变化相对于供气温度可忽略不计，压力对时间的导数可由能量方程和传热定律推导并结合公式(2)来描述[19]，有：

(4)

活塞杆运动时，腔室A的体积为：

Va=Aax+Vd

(5)

式中,Aa—— 活塞杆有效面积

Vd—— 死区容积

x—— 气缸活塞杆位移

把式(4)代入式(5)中，得腔室A中压力对时间的导数：

(6)

依据牛顿第二定律，气缸中活塞杆的运动方程为：

(7)

式中,F0—— 弹簧预紧力

k—— 弹簧刚度系数

β—— 黏性摩擦系数

m0—— 活塞杆质量

Ff—— 摩擦力，采用Stribeck模型

Fext—— 活塞杆受到的外部其他力的合力

因活塞杆外部没有负载且气缸水平放置，此项忽略不计。将式(6)对时间求导，并代入式(5)，可得活塞杆位移与流体流过芯片阀口的质量流量关系为：

(8)

(9)

3 实验研究

采用硅流体芯片的气动位置控制系统结构简图如图6所示，主要由三联件、采用双芯片结构的气动比例压力阀(可看成是一个二位三通阀)、单作用气缸(FESTO ESNU-12-25-P-A圆形气缸，气缸行程0～25 mm，缸径12 mm，运行压力0.15～1 MPa)、激光位置传感器(ANR1251，有效量程0～20 mm，最小分辨率0.001 mm)、数据采集卡(USB-6361, National Instruments)、压力传感器、控制器组成。当输入参考电压时，通过激光位置传感器检测出气缸活塞杆伸出的位置，并将其转换成电压信号反馈至控制器中，实现位置闭环控制，系统部分实物图如图7所示。

控制的气缸行程为0～10 mm,控制器内部对激光传感器反馈的电压信号进行了平均滤波处理，实验中对比了增量式PID及位置式PID两种控制算法的控制效果。由于采集到的实验数据受电路噪声的影响较

图6 气动控制系统结构简图

图7 气动控制系统部分实物图

大，对其进行了巴特沃斯滤波处理，表达式如下：

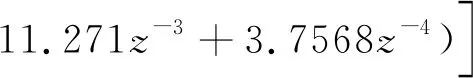
(10)

气源压力ps为0.7 MPa时，采用位置式PID控制输出的气缸活塞杆位移(x)曲线波动较大，采用增量式PID控制的系统阶跃响应输出结果随时间t的变化曲线如图8所示，系统阶跃响应上升时间小于0.247 s，当气缸行程为10 mm时上升时间最小为0.125 s，随着设置的气缸行程的增大，上升时间逐渐减小，这主要与实验中不同的行程分别设置了不同的控制器参数有关。系统的下降时间小于0.492 s，当气缸行程为2 mm 时，下降时间最小为0.2 s，随着设置的气缸行程增大，下降时间逐渐增大。其主要原因在于，芯片阀口的过流面积较小(最大为0.045 mm2)，过流能力较低，当气缸行程增大时，控制腔的体积也随之增大，从而导致了系统排气(下降)时间的增大。气缸输出位移与设定的气缸行程之间的误差e如图9所示，稳态后系统的误差小于0.077 mm,具有较高的定位精度。

气源压力为0.2 MPa时，分别采用增量式PID控制及位置式PID控制的阶跃响应实验结果如图10、图11所示，系统上升时间分别小于0.183 s和0.177 s，下降时间分别小于0.188 s和0.19 s，稳态后系统的定位误差分别小于0.105 mm和0.206 mm。

图8 气源压力为0.7 MPa时系统阶跃响应实验结果图

图9 阶跃响应误差图

图10 采用增量式PID阶跃响应输出结果图

图11 采用位置式PID阶跃响应输出结果图

对比以上实验结果可知，系统采用增量式PID的控制效果更好，在较高压力(0.7 MPa)时系统阶跃响应的控制精度最高， 但下降时间也最长。对比不同气

图12 不同气源压力下系统三角波滞回特性曲线图

图13 正弦信号响应实验结果及误差图

压源下，相同气缸行程的实验结果可知，系统下降时间还与气源压力有关，气源压力越大，下降时间越长。

气源压力分别为0.15， 0.2， 0.6 MPa时，输入的三角波控制电压信号U对应气缸活塞杆行程x的滞回特性曲线如图12所示。不同气源压力下，输入1 Hz的三角波信号，系统对应的滞回特性实验结果表明，随着气源压力的增大，输出的滞回回环逐渐扩大。

控制系统的正弦信号响应实验结果如图13所示，气源压力为0.7 MPa时，系统对正弦控制信号的跟随能力最差，最大误差为1.56 mm。随着气源压力的减小，系统的正弦信号响应能力逐渐增强，气源压力为0.2 MPa时，输入2 Hz的正弦控制信号系统可以较好的跟随，输出的误差小于1.18 mm。

图12及图13中的实验结果表明：气源压力的变化对控制系统的输入输出特性影响较大。分析其中原因如下：气源压力为0.7 MPa时，采用双芯片结构比例阀输出压力p的开环特性实验结果如图14所示，硅流体芯片本身存在一定的死区以及饱和区，线性可控制范围约在30%～60%。位置控制实验中不同气源压力下对系统进行标定时，输入控制电压均为0～5 V(0～100%)，对应的输出位移为0～10 mm，由于闭环控制对非线性的抑制能力有限，输入相同的控制电压，气源压力越大，进入控制腔室的气体压力也越大，对应的滞回回环及位置误差也随之增大。不同的气源压力，需对系统进行不同的标定，尽量避开芯片的死区及饱和区。若采用较大的气源压力，将控制电压输入范围选择在芯片线性控制区间的左侧(如30%～50%)，会有更好的控制效果。若采用的气源压力较小时，为避开芯片死区的影响，可将控制电压的输入范围选择在芯片线性控制区间的右侧(如40%～60%)。如图15所示，气源压力为0.15 MPa时，将输入的三角波信号偏置0.2 V，对应的滞回特性有所改善。

图14 双芯片结构比例阀开环特性实验结果

图15 控制信号偏置0.2 V滞回特性曲线图

4 仿真探讨

由于芯片的较小尺寸，限制了芯片的过流能力，但基于其方便集成安装的特性，通过增加芯片个数来提高过流能力改善控制系统的性能应该是值得尝试的。下面利用AMESim软件对气动控制系统进行仿真研究，探究并联入系统中的芯片个数对系统输入输出特性及滞回特性的影响。仿真模型如图16所示，部分仿真计算参数如表1所示。气源压力为0.7 MPa时， 输入的控制电压信号分别为0～5 V的阶跃信号和三角波信号对应的仿真结果与实验结果如图17所示，仿真是有效的。

图16 AMESim仿真模型图

表1 部分仿真参数

增加系统中并联的芯片个数，相当于增大了阀口的过流面积，如图17a所示，阶跃响应的上升、下降时间随着芯片个数的增加明显变小。采用四芯片及六芯片并联的控制系统三角波滞回特性曲线仿真结果如图18所示，增加芯片个数对系统的滞回特性有所改善，采用四芯片的系统滞回特性最好， 但仍未达到理想的控制效果。

图17 仿真与实验结果对比图

图18 不同芯片个数对应三角波滞回特性曲线图

4 结论

(1) 在采用增量式PID控制算法的情况下，采用硅流体芯片的气动位置控制系统具有较好的控制精度。硅流体芯片在气动控制系统上的应用对将来实现缸阀一体化、小型化具有一定的意义；

(2) 气源压力的变化对控制系统的输入输出特性影响较大。通过实验得到了不同气源压力下，系统对阶跃信号、三角波信号及正弦波信号的响应曲线。系统的阶跃响应下降时间、三角波滞回特性曲线回环会随着气源压力的增大而增大。系统的正弦信号跟踪能力会随着气源压力的增大逐渐减弱。在气源压力为0.7 MPa时，系统的阶跃响应控制精度最高，进入稳态后误差小于0.077 mm。当气源压力为0.2 MPa时，系统对2 Hz的正弦信号可以较好的跟随。在采用不同的气源压力时，需对系统进行不同的标定，尽量避开芯片的死区及饱和区，会有更好的控制效果；

(3) 利用AMESim软件对系统进行了仿真研究，仿真结果表明，增加芯片个数可减小阶跃响应的上升及下降时间，对滞回特性也有一定的改善。相较于采用六芯片及双芯片的控制系统，采用四芯片的系统滞回特性最好，但与理想的控制效果还有一定的差距。后期将通过控制算法及气缸结构参数的优化来达到更好的控制效果。