环形燃料芯块一维稳态温度场计算方法研究

马辉强 于 涛 陈珍平 赵鹏程 谢金森 刘紫静 刘建星雷洲阳 何清玲

1（南华大学核科学技术学院 衡阳421001）

2（南华大学湖南省数字化反应堆工程技术研究中心 衡阳421001）

环形燃料芯块具有优越的经济型和安全性［1］，受到了国内外的广泛关注。美国已将环形燃料确定为新一代核电燃料进行研发，且将其作为美国现役核电站延寿至80年研究计划中的首选燃料，麻省理工学院（Massachusetts Institute of Technology）针对环形燃料元件应用压水堆以提升堆芯功率密度做了深入研究［2-4］；韩国原子能科学研究所、中国原子能科学研究院分别对韩国标准型核电站“OPR1000”堆芯和秦山二期反应堆堆芯在不改变原有燃料组件尺寸和水铀比条件下，通过用环形燃料元件替代原有的棒状燃料组件进行了堆芯物理和热工水力分析［5-6］。

实心圆柱燃料芯块温度场求解方法无法获得环形燃料芯块温度场的分布，差分和有限元方法计算燃料芯块温度场分布相对耗时，不利于大规模计算，有必要分析环形燃料芯块温度场计算的方法，以提高环形燃料芯块温度场的计算精度和计算效率。本工作针对环形燃料芯块，从导热微分方程和傅立叶定律出发，导出了环形燃料芯块平均热导率计算方法，建立环形燃料芯块稳态温度场分布、最高温度以及最高位温度位置的模型，并验证该模型的正确性。

1 环形燃料芯块温度场模型

1.1 径向最高温度位置

双面冷却的环形燃料芯块的导热存在热量分配问题［6］，芯块中的热量分别从芯块内外表面中导出，芯块内外表面各自导出热量的多少取决于芯块内侧和外侧的热阻大小。实心圆柱燃料芯块的最高温度的位置一般在芯块的中心轴上，最高温度容易求解；环形燃料芯块中的最高温度以及最高温度的位置是随内外两侧热阻的变化而变化［7］。环形燃料芯块中需要确定最高温度的位置后才能计算环形芯块的最高温度［8］，最高温度位置通过傅立叶定律和积分热导率进行计算。环形芯块内外表面温度由环形燃料元件的对流换热计算得到，本工作采用文献［9］中的计算得到芯块内外表面温度。环形燃料芯块模型示意图如图1所示。

图1 环形燃料芯块模型Fig.1 Model of annular fuel pellets

忽略轴向导热，环形燃料芯块中傅立叶定律为［10］：

式中：kf（t）为燃料芯块的热导率函数，W·m-1·K-1；qv为燃料芯块的功率密度，W·m-3；rm为芯块中绝热面（即芯块径向最高温度的位置）的半径，m。对式（1）两端同时积分并简化，得到环形燃料芯块的积分热导率：

式中：ru和tu分别表示芯块表面处的半径和温度。再将式（2）简化得到积分热导率的最终的形式：

假设环形燃料芯块的最高温度出现在径向rm处，分别从燃料芯块的内外表面出发，从芯块两侧往中间计算，可以得到在rm处燃料芯块温度的表达式，且这两式相等，即：

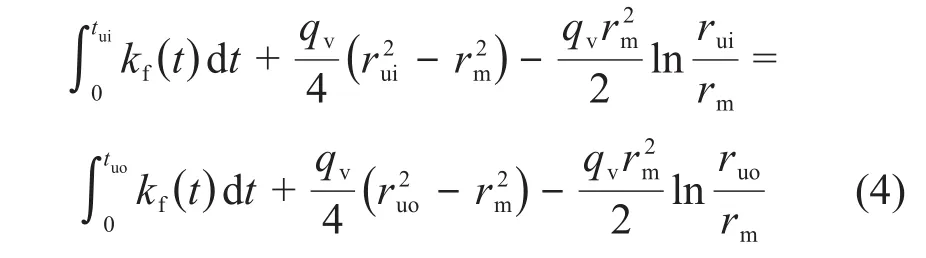
然后得到芯块中最高温度的位置rm为：

1.2 芯块温度场计算

忽略轴向导热，由圆柱坐标系一维稳态传导热微分方程导出环形燃料芯块径向温度分布。环形燃料芯块导热微分方程方程和边界条件［11］为：

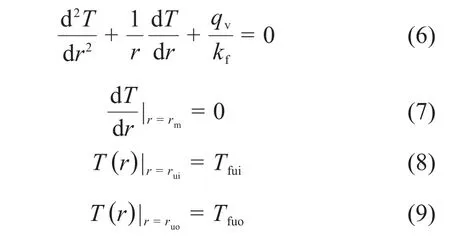
式中：r为燃料芯块半径，m；燃料芯块的内外表面半径分别为rui和ruo，m；Tfui、Tfuo分别为燃料芯块内外表面的温度，K；kf为燃料芯块的平均热导率，W·m-1·K-1。对于式（6）的解来说，边界条件（8）和（9）是等价的。式（6）的通解为：

UO2等核燃料的热导率随温度而变化，若要确定环形燃料芯块一维稳态温度分布，则需要准确地确定式（6）中芯块的平均热导率kf（在导热介质所处的温度范围内用一个热导率常数等效替换对随温度变化的热导率）。对于稳态情况，芯块内外表面温度确定后，环形燃料芯块绝热面的位置则可以确定，分别从燃料芯块的内外表面出发，从两侧往芯块中间计算，在绝热面位置处式（11）中两个函数计算结果必须相等，由此可得出绝热面rm的位置：

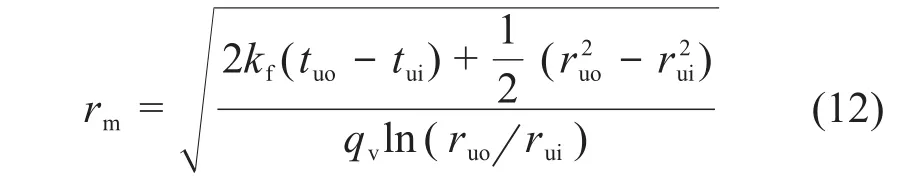
联立式（4）、（11）得到环形燃料芯块的平均热导率kf：

由式（12）可以发现环形燃料芯块的平均热导率与传统实心芯块的平均热导率的计算方法具有一定差异，环形燃料芯块的平均热导率主要取决于芯块内外表面温度。根据数学极限，当tui=tuo时，kf=kf（tui）=kf（tuo），当r=rm时可求得芯块中的最高温度tmo。

综上，式（5）、（11）、（13）即为从导热微分方程和傅立叶定律得出的环形燃料芯块稳态一维温度场分布模型。

1.3 芯块温度场计算修正

求解环形燃料芯块的温度场分布的关键在于求解芯块的平均热导率。由于环形燃料芯块的热导率可能较低，与温度呈非线性关系变化，且随温度变化幅度较大（如二氧化铀），对于较厚的环形燃料芯块，芯块表面与绝热面之间温度梯度将变得更加陡峭，从而使热导率对空间位置产生较强的依赖性，即热导率随燃料芯块径向位置的变化幅度大，最终导致式（13）计算的芯块平均热导率偏大，温度越高偏差越大。针对这个问题，由式（5）、（12）确定了绝热面位置后，根据已知的芯块表面温度tui、tuo和进一步得出的芯块绝热面位置rm以及修正前的绝热面最高温度tmo，然后将环形燃料芯块从绝热面位置分成内外两层圆柱环，根据式（14）分别修正内外两侧的芯块平均热导率kfi和kfo，然后由式（15）分别求解内外环的温度场，最高温度取两侧计算的平均值。

2 模型验证

为了验证模型的正确性，基于本文构建的计算模型开发了环形燃料芯块温度场计算程序PTFA（Program of Temperature Field of Annular Fuel Pellets），计算不同功率密度、不同芯块厚度下的绝热面位置、最高温度以及芯块的温度场分布，并与有限元程序COMSOL5.4［12］计算的结果进行对比验证，对比两种方法计算结果的相对偏差。

2.1 模型参数

根据现有文献［13-14］，反应堆正常工况下的最高线功率密度为61 kW·m-1，同时参考已有的文献中环形燃料的线功率密度参数［12］，选择环形燃料芯块线功率密为36 kW·m-1、54 kW·m-1以及71 kW·m-1进行计算，采用的热导率函数为95%理论密度二氧化铀的热导率［12］，现有研究成果表明：环形燃料芯块的厚度的范围一般不超过3 mm［2，15］。验证模型和参数如图2和表1、表2所示。在COMSOL5.4中建立一维环形燃料芯块模型，芯块上下表面设为绝热边界条件，确定芯块内外侧表面温度，并对其进行细网格划分，设置好芯块的热源和热导率函数后采用COMSOL5.4的固体导热模块求解不同厚度环形燃料芯块的各个功率密度工况的一维稳态温度场。

图2 环形燃料芯块COMSOL5.4计算模型Fig.2 COMSOL5.4 calculation model of annular fuel pellet

表1 环形燃料芯块模型参数Table 1 Parameters of annular fuel pellets model

表2 不同厚度环形燃料芯块的体功率密度及表面温度Table 2 Power density and surface temperature of annular fuel pellets with different thickness

2.2 结果分析

核反应堆设计和运行中，燃料芯块的温度是一个非常重要的参数。对于环形燃料芯块需要准确地得到芯块的温度场，包括绝热面位置、芯块最高温度等。本模型的验证主要针对绝热面位置、芯块最高温度以及芯块中温度场分布等进行。

2.2.1 芯块绝热面位置

环形燃料芯块绝热面的位置决定环形燃料元件内外冷却通道的热量分配比，从而影响内外通道冷却剂流量的分配和冷却剂的压降，最终决定着环形燃料元件的导热性能，影响环形燃料元件的安全性和经济性。不同功率密度下、不同芯块厚度的环形燃料芯块，PTFA和有限元程序COMSOL5.4计算的最高温度位置如表3所示。结果表明：对于绝热面的位置的计算，PTFA计算结果与COMSOL5.4计算的结果符合很好，二者之间最大偏差小于0.15%，验证了环形燃料芯块温度场模型计算绝热面位置的正确性。

2.2.2 芯块绝热面最高温度

环形燃料芯块的最高温度是评价燃料元件性能的重要参数之一，准确地获得燃料芯块的温度对环形燃料元件裂变气体释放率、肿胀、使用寿命和燃耗计算是十分必要的。对于不同功率密度下、不同芯块厚度的环形燃料芯块，PTFA和有限元程序COMSOL5.4计算的绝热面最高温度如表4所示。结果表明：对于环形燃料芯块最高温度的计算，PTFA计算的结果与COMSOL5.4计算的结果符合很好。采用未修正的芯块平均热导率计算的芯块最高温度结果总体相对于COMSOL5.4计算的结果稍微偏小，二者的相对偏差小于1.5%，这是由于二氧化铀热导率较低，导致芯块中温度梯度较大，从而使热导率对空间位置产生较强的依赖性，最终导致式（13）计算的芯块平均热导率偏大。采用修正后的芯块平均热导率时，PTFA计算的最高温度与COMSOL5.4计算的结果相对偏差小于0.2%，显著提高了计算精度，验证了环形燃料芯块温度场模型 计算环形燃料芯块绝热面最高温度的正确性。

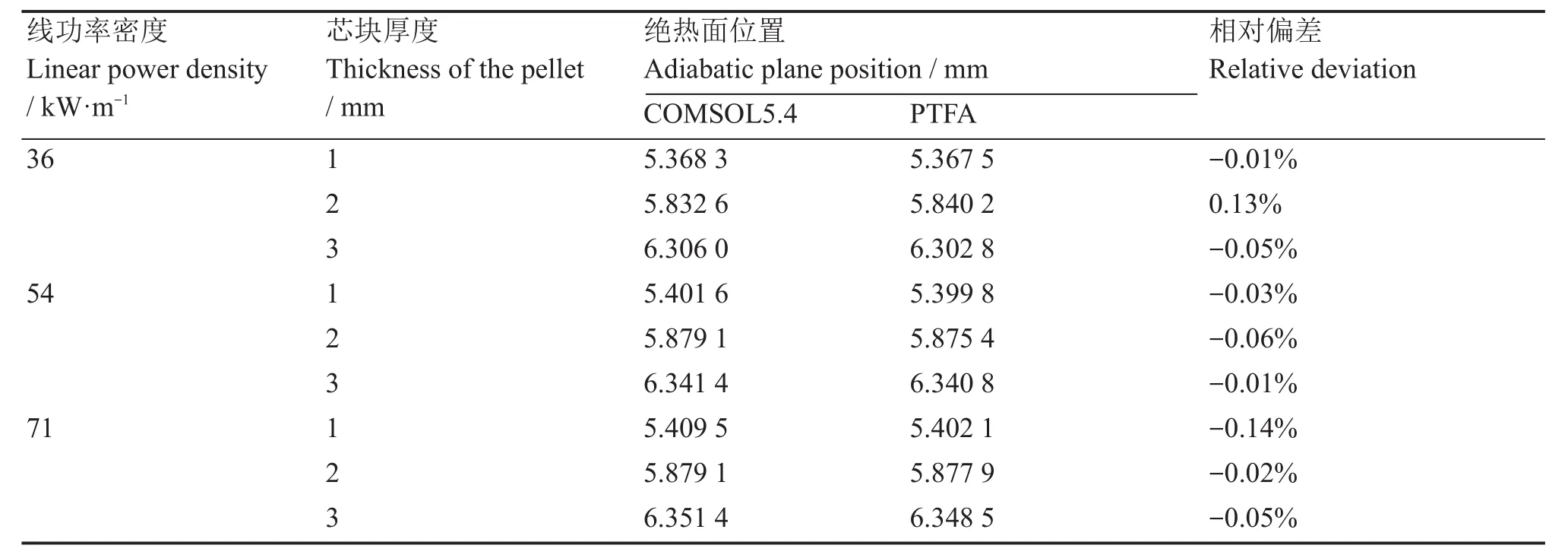
表3 不同线功率密度下环形燃料芯块绝热面位置Table 3 Position of insulation surface of annular fuel pellets under different linear power densities

表4 不同线功率密度下环形燃料芯块最高温度Table 4 Maximum temperature of annular fuel pellets under different linear power densities

2.2.3 芯块温度场分布

如图3所示，对于不同功率密度下、不同芯块厚度的环形燃料芯块，PTFA与有限元程序COMSOL5.4计算的温度场分布符合较好。由于二氧化铀热导率较小引起环形燃料芯块中温度梯度较大，从而引起热导率对空间位置较强的依赖性，温度越高，依赖性越强，采用未修正的芯块平均热导率计算的芯块最高温度总体相对于COMSOL5.4计算的结果稍微偏小，且两者间的温差随着芯块温度的增加而增加。修正后的热导率将整个芯块的平均热导率以绝热面为中心分为内外两个区域的平均热导率，减弱了热导率对空间位置的依赖性，采用修正后的芯块平均热导率计算时，PTFA计算的温度场分布与有限元程序COMSOL5.4计算的温度场分布符合得非常好，相对偏差很小。对于热导率较小或热导率随温度变化较大的燃料芯块的温度场计算，采用修正后的燃料芯块平均热导率进行计算以获得较为精确的计算结果。

2.2.4 环形燃料芯块厚度对温度场的影响

如图3所示，环形燃料芯块厚度相同时，增大燃料芯块的功率密度，燃料芯块的最高温度明显升高，芯块内部的温度梯度将变得更加陡峭。结合表1、3、4，当燃料芯块的线功率密度和芯块内外表面温度一定时，环形燃料芯块越厚，芯块的体功率密度越小，芯块的最高温度越高；环形燃料芯块越薄，芯块的体功率密度越大，芯块的最高温度越低。所以减小芯块的厚度比降低燃料芯块功率密度更能有效降低环形燃料芯块的运行温度。

图3 不同芯块厚度（1 mm、2 mm、3 mm）和不同线功率密度（36 kW·m-1、54 kW·m-1、71 kW·m-1）下环形芯块温度场Fig.3 Temperature field of annular fuel pellets under different thickness(1 mm,2 mm,3 mm)and different linear power density(36 kW·m-1,54 kW·m-1,71 kW·m-1)

3 结语

本文根据导热微分方程和傅立叶定律，针对环形燃料的芯块建立了环形燃料芯块一维稳态温度场计算模型，导出了环形燃料芯块绝热面位置以及燃料芯块最高温度的计算方法。并对该模型进行了验证和分析，得出了以下结论：

1）环形燃料芯块一维稳态温度场计算关键在于准确计算环形燃料芯块最高温度的位置以及平均热导率。利用修正后的平均热导率计算的环形燃料芯块温度场结果与COMSOL5.4计算结果的相对误差小于2‰，该模型可以用于环形燃料元件的热工水力分析，具有较高的计算精度和效率。

2）减小芯块的厚度比降低燃料芯块功率密度更能有效降低环形燃料芯块的运行温度。