拦沙坝非线性地震响应分析及极限抗震能力研究

陈天燊，刘 智，赵兰浩，李同春,2

(1. 河海大学水利水电学院，南京 210098；2. 河海大学水资源高效利用与工程安全国家工程研究中心，南京 210098)

0 引 言

随着水电站工程的不断开发，在流域水电整体规划中将会面临以包含断层等不利结构的岩体作为大坝基础的问题[1]。而断层影响带和断层破碎带一起，共同构成了地下水的主要储聚场所，导致这一区域具有强度低、变形大、透水性强等特征，该地段的存在可能会给水库和大坝带来重大安全隐患[2]，因此有必要对其进行研究。

印度Koyna重力坝作为遭受震害的典型工程，众多学者采用各类方法对其破坏模式进行数值模拟时将地基作为线弹性材料处理[3,5]，因此大坝坝踵处不可避免地出现应力集中区域，但震后坝基交界处无明显破坏，这主要是由于地基线弹性模型不能反映其损伤情况所致。因此，进一步考虑计入地基岩体损伤的深化研究十分必要。在分析重力坝极限抗震能力时，张社荣等[6]和涂劲[7]等均采用D-P屈服准则对坝基破坏进行分析，而钱声源等[8]使用Mohr-Coulomb本构模型模拟地基材料在地震中的塑性屈服特性。但对于岩体等准脆性材料，直接采用经典的弹塑性损伤模型而不考虑岩体特性的可靠性备受争议[9]。进一步地，坝基面附近的损伤演化情况势必会对阻滑能力产生影响，进而需要对坝体-地基系统的损伤、渗流场变化以及建基面抗滑稳定安全系数时程曲线进行综合分析，而目前对于这方面的研究还有所欠缺。

鉴此，本文以某抽水蓄能电站下水库拦沙坝河床坝段为例，采用坝体-地基系统损伤模型以及断层损伤-渗流耦合效应，通过不断增加地震动输入来研究断层的材料非线性对于坝体动力响应以及建基面抗滑稳定的影响，旨在对复杂地基条件下的重力坝做出更为有效的抗震安全评价。

1 计算模型与计算原理

1.1 坝体-地基系统损伤软化模型

坝体混凝土采用基于四参数等效应变的损伤本构模型[10]，其不仅适用于多轴应力状态下混凝土受力的全过程，且能够同时考虑受拉和受压损伤，已经应用于高混凝土坝超载地震抗震分析[11]，其破坏准则如下：

(1)

式中：I1为应变张量第一不变量；J2为应变偏量第二不变量；ε1为最大主应变；εp混凝土抗拉强度下的极限应变；A、B、C、D4个参数则通过混凝土材料参数联立求得[10]。

天然岩体是一种非均匀材料，内部含有大量的空隙、微裂缝等多种天然缺陷，这些天然缺陷称为岩体的初始损伤[12]。而断层破碎带以及断层影响带中的缺陷显然更加密集，单元的初始损伤难以用一个给定的数值来反映。但是，可以通过Weibull分布赋值来描述。对于岩石类的脆性材料，目前有基于Weibull分布的岩石损伤软化模型[13]，其表达式为：

σ1=Eε1exp[-(F/F0)″]+μ(σ3+σ2)

(2)

式中：F为服从Weibull分布的岩石微元强度；m及F0为Weibull分布参数；σ1、σ2、σ3和ε1分别为岩石的名义应力和应变；E和μ分别为岩石的弹性模量和泊松比。

基于Drucker-Prager破坏准则的岩石微元强度F的表达式为：

(3)

I1=α0(σ1+2σ3)Eε1/(σ1-2μσ3)

(4)

(5)

1.2 损伤-渗流耦合效应

断层的损伤演化过程中，材料的渗透性将会逐渐上升，当荷载过大使初始空隙、微裂缝扩展以至于贯通时，材料的渗透性能会发生急剧上升，即发生渗透系数的突跳现象。通常采用C.Louis根据试验总结得出的应力-渗流耦合公式，并根据突跳现象补充岩体损伤值对渗透性突跳系数取值的影响：

(6)

式中：K0为渗流系数初值；β为应力-渗流耦合系数；σ为有效应力；p为孔隙水压力；D为岩体损伤值；ξ为渗透性突跳系数，表达式为：

(7)

其中当断层损伤值D为0时，突跳系数ξ取为500[14]，而断层裂隙的损伤演化是一个持续的过程，突跳系数随损伤的增加而增大[15]。

2 有限元网格模型与参数

2.1 工程概况

某抽水蓄能电站主要建筑物由拦河坝、拦沙坝和右岸泄洪排沙洞组成，其中拦沙坝为碾压混凝土重力坝，坝顶高程934 m，建基面高程886 m。拦沙坝坝址区共有发育断层7条，其中断层F10规模较大，其余断层规模较小，宽度一般小于5 cm。根据工程地质勘测资料，断层F10走向NW300～330°，陡倾NE∠50°～75°，自拦沙坝河床坝基处通过。由断层或裂隙密集带所造成的岩石强烈破碎的地段称为断层破碎带，断层F10的断层破碎带与坝轴线夹角为35°～55°，宽度为15～20 m并由次级小断层组成；而在离开断层主断面一定距离内出现的不同于正常岩层分布区特征的异常带称为断层影响带，断层F10的断层破碎带两侧的断层影响带宽度为15～20 m，影响带内岩体破碎，断层及其影响带坝段存在岩体浅层剪切破坏。根据地质勘测资料，沿断层不存在深层抗滑稳定问题。本工程场址地震烈度为Ⅷ度，依据现行规范的有关规定，取相应于100年超越概率为2%的基岩水平峰值加速度进行抗震设计。

2.2 计算材料参数

重力坝材料分区以及断层材料分布如图1所示，为了能够更好地模拟断层损伤对坝体抗震性能的影响，忽略设计中的固结灌浆以及混凝土塞，这样会使计算结果偏于危险，而依据计算结果对坝体采取的防护措施将偏于安全。坝体混凝土、基岩以及断层静态材料参数如表1所示，混凝土与岩体间的抗剪断参数如表2所示，由于地质勘测资料中未给出断层的渗透系数，根据张培兴等[16]的研究分别取断层破碎带和断层影响带渗透系数为10-6和10-7。材料动态参数在静态情况下根据《NB 35047-2015水电工程水工建筑物抗震设计规范》将弹性模量提升50%，抗压强度提升20%。

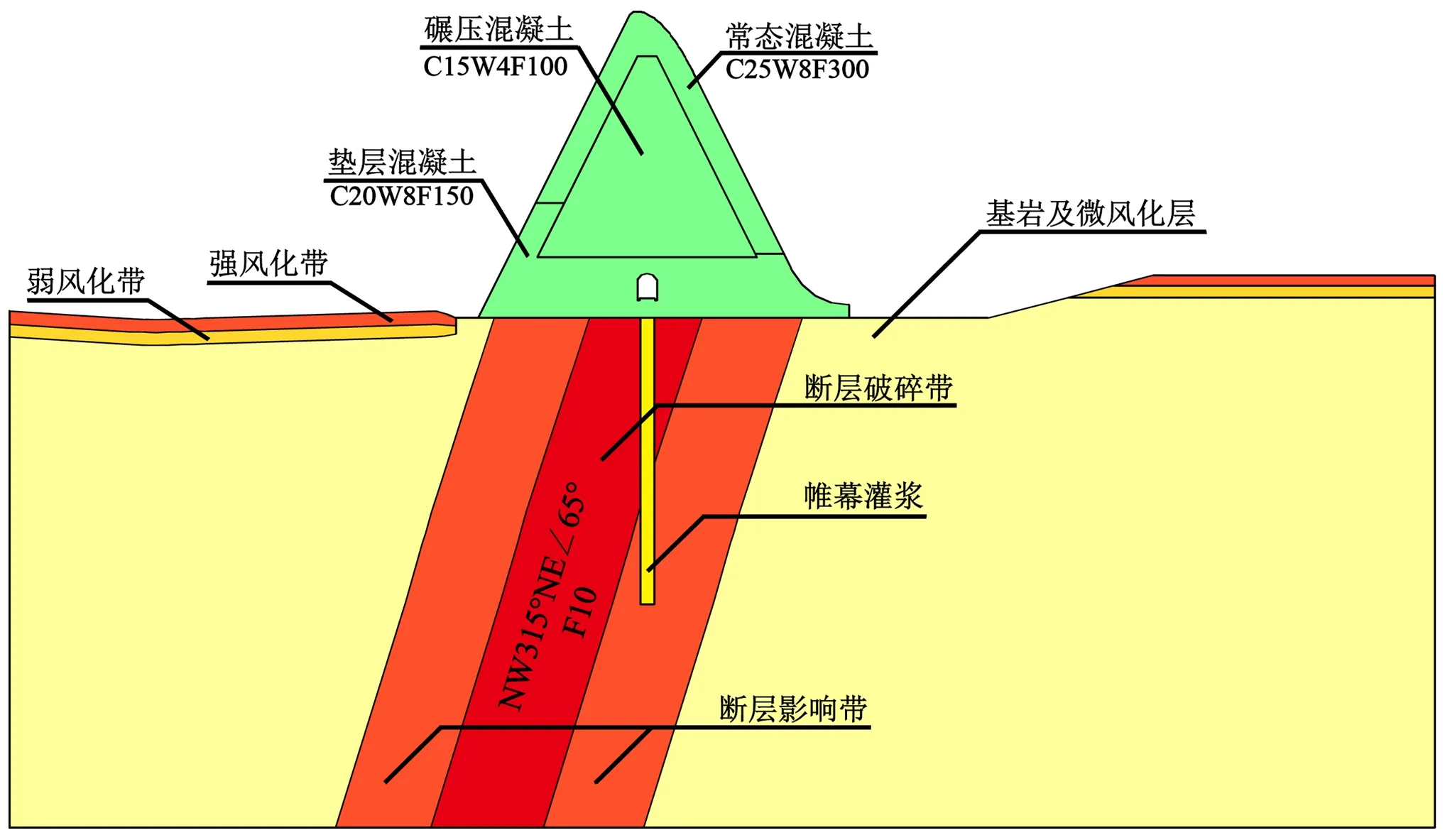
图1 坝体以及地基材料分区Fig.1 Dam and foundation material partition

表1 混凝土以及地基材料参数Tab.1 Concrete and foundation material parameters

表2 混凝土/岩体抗剪断参数Tab.2 Concrete/rock mass shear resistance parameters

根据上述混凝土材料参数中的抗压强度、抗拉强度、弹性模量和泊松比，可求得混凝土四参数损伤本构模型的A、B、C、D4个参数取值如表3。而各地基材料分区采用的基于Weibull分布的岩石损伤软化模型参数m及F0如表4，往往岩体强度越低，岩体缺陷越多，则非均匀性越强，即形状参数m越大[12]，而F0的取值与m相关[13]。

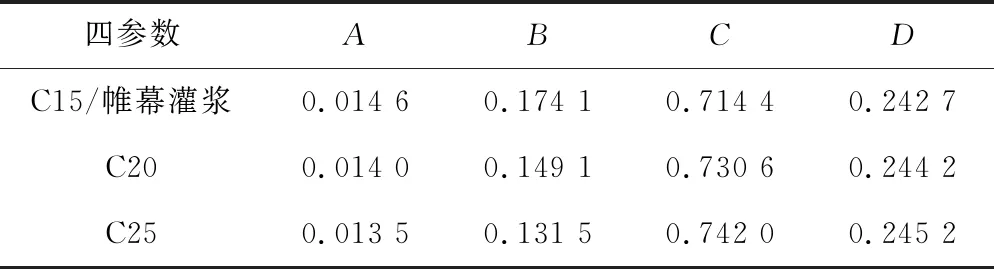
表3 混凝土四参数损伤本构模型参数Tab.3 Four-parameter damage constitutive model parameters of concrete

表4 基于Weibull分布的岩石损伤软化模型参数Tab.4 Parameters of rock damage softening model based on Weibull distribution

2.3 有限元网格模型以及作用荷载

水体-坝体-地基计算模型网格如图2所示，计算范围分别从坝踵和坝趾向上、下游延伸1.5倍坝高，地基深度取1.5倍坝高，采用自主编程的FORTRAN有限元程序进行计算。因为本文要计算动力荷载下渗流场的时程变化，所以在坝体上游建立水体网格并采用两相流固耦合的方式来代替Westgaard附加质量法，以此来对断层损伤后的渗透系数突跳现象进行模拟仿真。

图2 水体-坝体-地基计算模型网格Fig.2 Water-dam -foundation meshing model

计算荷载包括静力荷载和地震动输入。首先进行静力计算，静力荷载包括：上下游静水压力、坝体自重、坝前淤沙压力、浪压力、扬压力。以静力计算结果为初始条件，采用考虑黏弹性人工边界的动力时程法进行结构动力分析，从坝体底边界和侧边界输入地震波，并且在上下游河床面施加水头约束来建立地基系统的饱和流场。根据《某抽水蓄能电站工程场地地震安全性评价》，按100年超越概率为2%时的基岩水平加速度峰值为0.277 g进行抗震设计。因此，其设计地震水平峰值加速度采用0.277 g，竖向加速度取为水平向的2/3，地震持续时间40.96 s，设计地震加速度时程曲线如图3所示。本文采用将设计地震加速度时程曲线乘以倍数N来不断增加地震动输入，倍数N称为设计地震超载倍数。

图3 设计地震加速度时程曲线Fig.3 Design seismic acceleration time-history curve

本文的有限元分析思路为：坝体均使用四参数损伤本构模型。在地基线弹性模型中地基使用线弹性本构模型；在地基非线性模型中，地基采用基于Weibull分布的岩石损伤软化模型，计算渗流场的同时考虑损伤-渗流耦合效应。对以上两种模型分别进行动力时程法计算，得到坝体和地基的损伤结果，并通过对每一时刻的建基面抗滑稳定进行计算，得到抗滑稳定安全系数时程曲线。

3 计算结果分析

本文首先计算了地基线弹性模型的结果，进而采用地基非线性模型来讨论坝体底部地基中断层的材料非线性对坝体抗震能力的影响，并且考虑了当断层出现损伤时抗渗能力的降低，此时坝体受到的孔隙压力也随地震作用变化，因此能够精细地捕捉到断层在地震作用下的材料行为对坝体材料破坏的影响。为了能够对坝体抗震能力进行全面评价，将对坝体-地基系统的损伤、渗流场变化以及建基面抗滑稳定安全系数时程曲线进行综合分析。

3.1 地基线弹性模型计算结果

图4～图5分别为1.0倍设计地震和2.18倍设计地震作用下的坝体损伤分布结果，图6为2.18倍设计地震作用下的建基面抗滑稳定安全系数时程曲线。在设计地震工况下，从图 4中设计地震坝体损伤结果可知，在上游水位较高时，不对称体型的重力坝只会在坝踵处产生损伤区域，但由于拦沙坝体型较为对称，所以在坝踵和坝趾均出现了损伤区域。而廊道底部和顶部也同时出现了损伤，这是由于坝底断层弹性模量较小，导致廊道底部处的沉降大于其余坝底部位的沉降，从而发生“拱效应”，使得廊道底部与断层之间的部位出现了拉应力。如图 5所示，当设计地震超载倍数N达到2.18时，坝踵和坝趾的损伤区域不断向坝体中部延伸，而廊道底部周围的损伤区域也到达了坝底，即建基面大部分区域已经进入损伤软化阶段。由图6可见此时建基面抗滑稳定安全系数时程曲线的最小值出现在7.68 s，小于《混凝土重力坝设计规范_SL319-2005》要求的最低限值2.3[17]，即坝体可能出现瞬时滑动，可认为此时坝体发生滑动失稳的可能性大大增加。

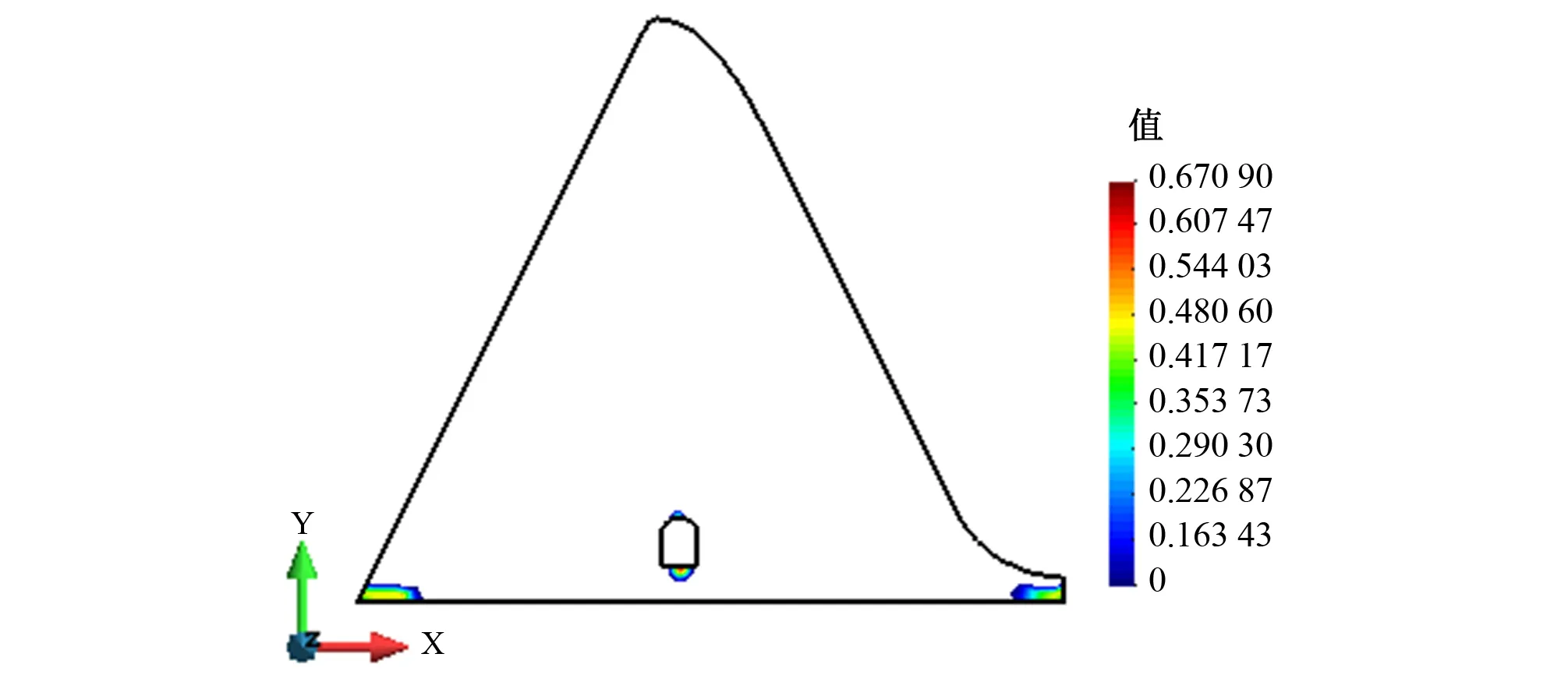
图4 设计地震坝体损伤结果Fig.4 Design seismic damage results

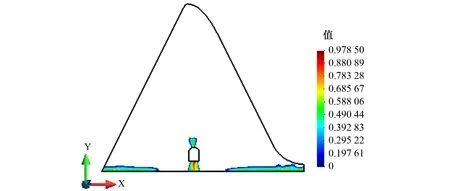
图5 2.18倍设计地震坝体损伤结果Fig.5 2.18 times design seismic damage results

图6 2.18倍设计地震抗滑稳定安全系数时程曲线Fig.6 2.18 times design seismic anti-sliding stability safety factor time-history curve

3.2 地基非线性模型计算结果

图7～图9分别为1.0倍设计地震和2.3倍、2.67倍设计地震作用下的坝体-地基系统的损伤分布结果。由图7可知，与地基线弹性模型计算结果相比，由于地基损伤的出现、发展，使得坝体底部的应力发生重分布，从而显著降低了坝体坝踵和坝趾处的损伤分布。随着地震动输入的不断加大，坝踵和坝趾的损伤区域逐渐沿着断层倾向发展。值得注意的是，由于断层的存在导致坝体廊道底部出现了较大的拉应力区；由图8可知，当设计地震超载倍数N达到2.3时，廊道的底部和顶部出现损伤区域，且廊道底部的损伤区已经向防渗帷幕上游侧的断层破碎带延伸；由图9可知，当设计地震超载倍数N达到2.67时，坝踵处的损伤区域突然向廊道底部扩展，使得坝踵和廊道底部的损伤区域贯通，导致防渗帷幕破坏且渗透系数急剧上升，发生突跳现象，地震前后的渗流场变化如图10所示。帷幕下游侧的孔隙压力增加导致建基面法向压力减小，且如图9(b)所示此时断层靠近建基面附近大部分区域已经发生损伤，抗滑能力降低，对坝体的抗滑稳定产生不利影响。

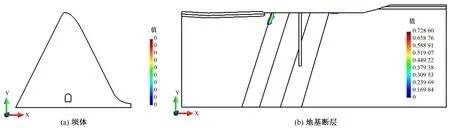
图7 设计地震坝体-地基系统损伤分布Fig.7 Design seismic dam-foundation system damage distribution

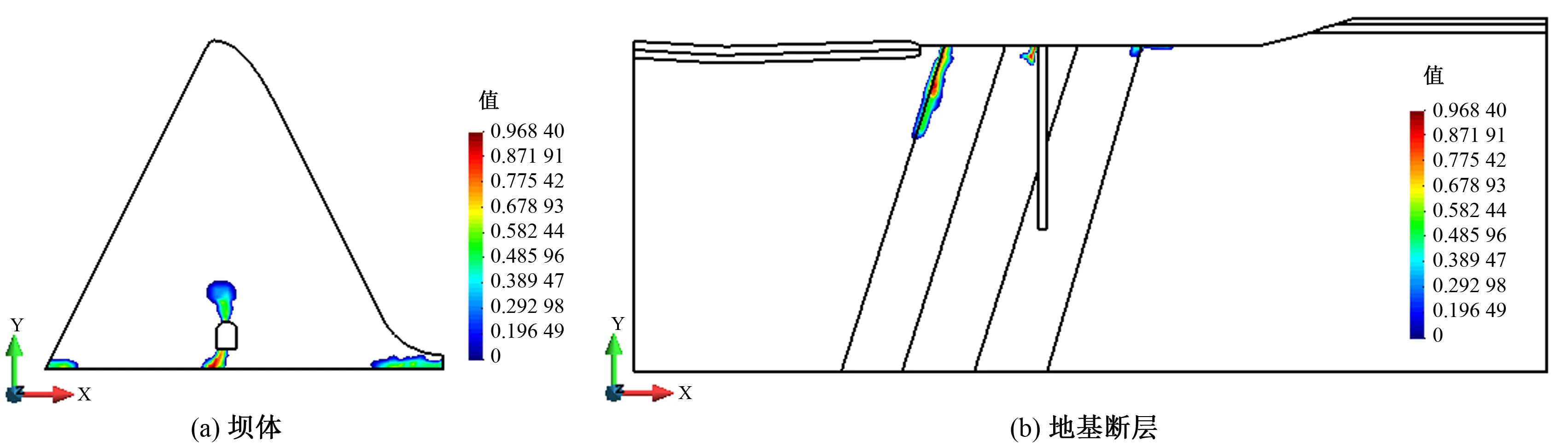
图8 2.3倍设计地震坝体-地基系统损伤分布Fig.8 2.3 times design seismic dam-foundation system damage distribution

图9 2.67倍设计地震坝体-地基系统损伤分布Fig.9 2.67 times design seismic dam-foundation system damage distribution

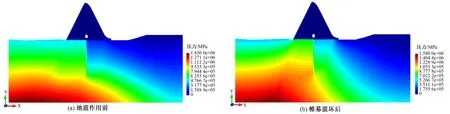
图10 2.67倍设计地震地基系统渗流场分布图Fig.10 2.67 times design seismic foundation system seepage field distribution

图11为2.67倍设计地震作用下的建基面抗滑稳定安全系数时程曲线，图12为地基线弹性模型和地基非线性模型的抗滑稳定安全系数时程曲线最小值与设计地震倍数的关系曲线。从图 11可见当设计地震超载倍数达到2.67时，抗滑稳定安全系数时程曲线最小值出现在8.18 s，此时已小于《混凝土重力坝设计规范_SL319-2005》要求的最低限值2.3[17]，即坝体可能出现瞬时滑动。由图12可知，随着设计地震超载倍数N的增加，当防渗帷幕发生破坏前，坝体-地基系统损伤模型的抗滑稳定安全系数时程曲线最小值比线弹性地基模型的抗滑稳定安全系数时程曲线最小值降低得慢，而当帷幕被震坏后，坝体-地基系统损伤模型的抗滑稳定安全系数时程曲线最小值急剧下降，有明显的转折处，由此可判断坝体-地基系统损伤模型是在断层带发生损伤并导致帷幕震坏后出现失稳，即坝体在超载地震下发生滑动破坏的主要原因是帷幕震坏和断层大面积损伤，显然坝体-地基系统损伤模型能够更真实全面地模拟断层对坝体极限抗震能力的影响。

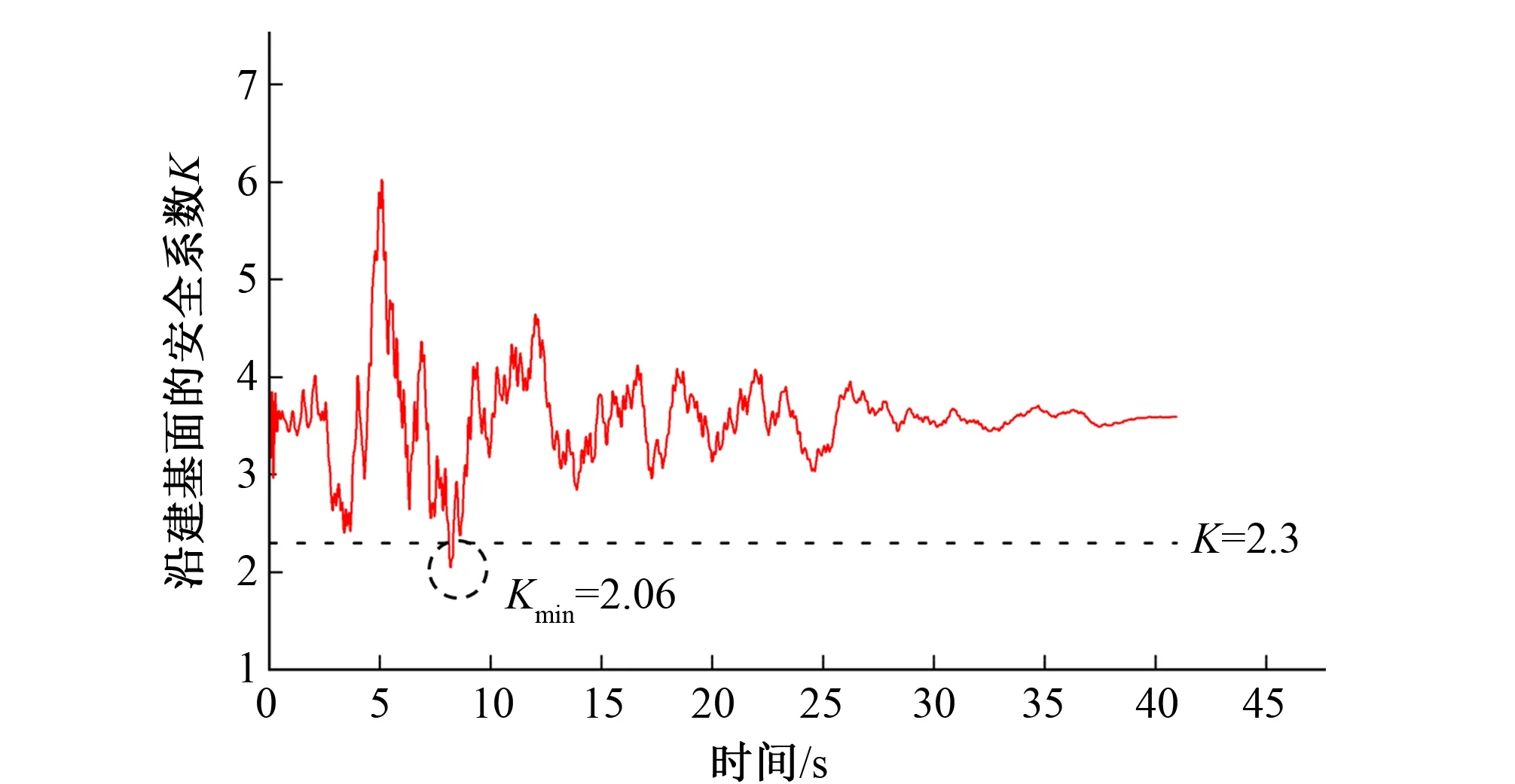
图11 2.67倍设计地震抗滑稳定安全系数时程曲线Fig.11 2.67 times design seismic anti-sliding stability safety factor time-history curve

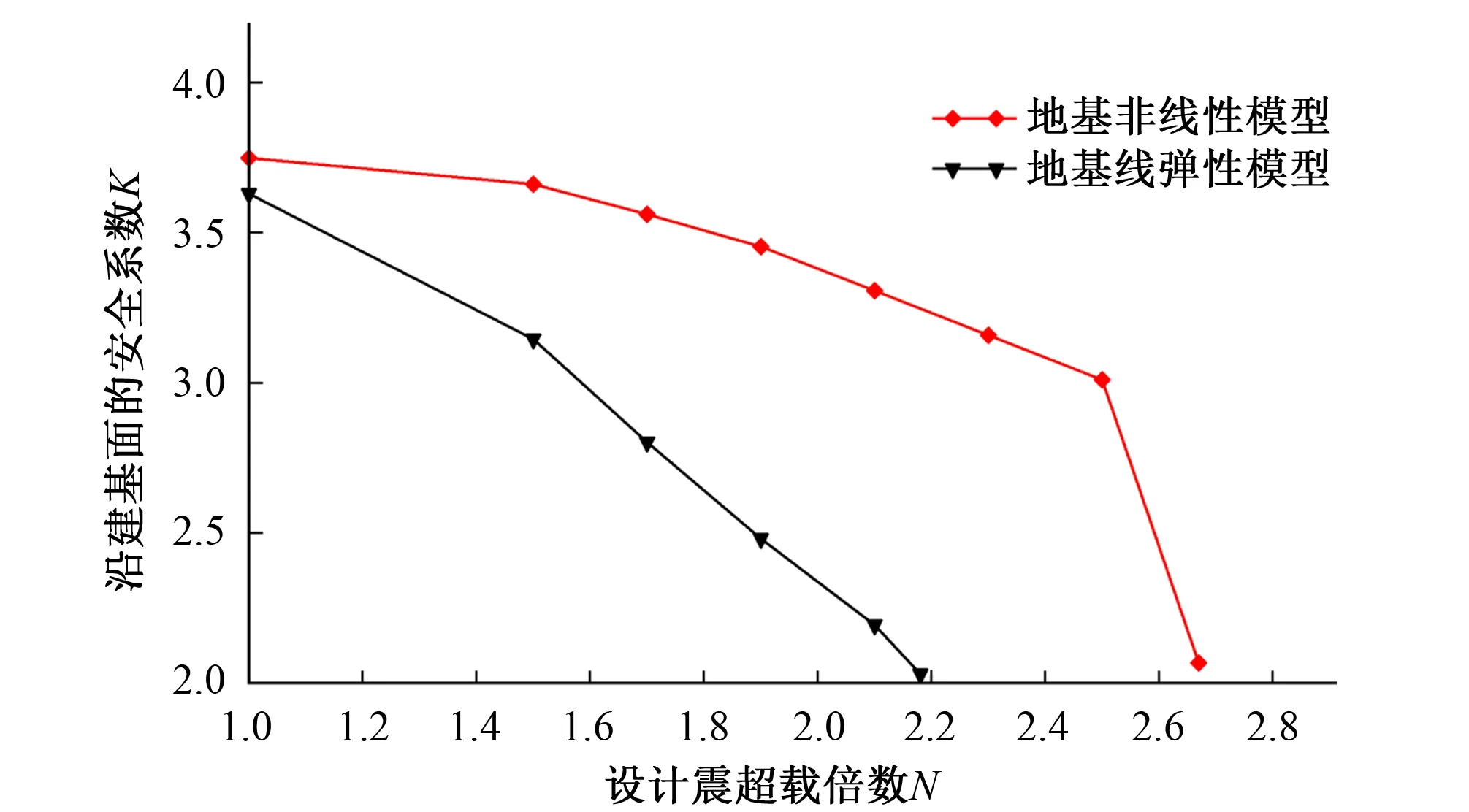
图12 抗滑稳定安全系数时程曲线最小值与设计地震倍数的关系曲线Fig.12 The relationship between the minimum value of the anti-sliding stability safety factor time-history curve and the design seismic multiplier

4 结 论

本文分别采用地基线弹性模型和地基非线性模型，对某抽水蓄能电站拦沙坝进行了极限抗震能力研究，基于建基面抗滑稳定安全系数时程曲线最小值低于《混凝土重力坝设计规范SL319-2005》的最低限值为失效破坏依据，通过比较两个模型的计算结果来对断层损伤以及损伤-渗流耦合效应对坝体抗震能力的影响进行探讨。得到结论如下。

(1)重力坝底部地基中的断层对廊道顶部和底部的应力状态有较大影响，而考虑地基材料非线性后廊道周围的损伤有所降低。

(2)考虑地基非线性后，坝踵、坝趾处地基和廊道底部断层破碎带产生损伤，当设计地震超载倍数N较大时，地基中的以上损伤区域将会贯通，且防渗帷幕发生破坏，渗透系数急剧上升，对坝体抗滑稳定造成不利影响。

(3)综合考虑地基断层材料非线性以及损伤对渗流场的影响能够更为真实地模拟复杂地基条件下的重力坝极限抗震能力。

□