斜拉桥Π形结合主梁施工过程剪力滞系数变化规律
2020-06-15郭飞周世军
郭飞,周世军
(1.广铁集团广州工程建设指挥部,广州 510440;2. 重庆大学 土木工程学院; 山地城镇建设与新技术教育部重点实验室,重庆 400045)
斜拉桥因其显著的跨越能力和较为合理的经济性能而成为大跨度桥梁中一种重要的结构形式。П形截面或П形组合截面是目前实际工程中常用的斜拉桥截面型式。与一般箱梁截面相比,斜拉桥中П形截面(或П形组合截面)主梁的宽高比较大(一般大于10),在弯矩、轴力共同作用下,混凝土翼板剪力滞效应相比普通箱梁更加显著,截面正应力沿翼板宽度的分布规律也变得十分复杂。而随着现代交通发展的需要,实际工程对组合梁斜拉桥的宽度和跨径要求越来越大,其主梁截面剪力滞效应问题也更加突出。因此,很有必要研究П形截面或П形组合截面斜拉桥在实际工程应用中的剪力滞效应。
许多学者针对剪力滞效应已进行了大量研究。Reissner[1]最早假设翼板纵向位移沿横向为二次抛物线分布,采用基于最小势能原理的能量变分法分析了矩形箱梁剪力滞效应。随后,许多学者[2-3]对Reissner的方法进行扩展,进行了大量理论研究和试验验证,并在已有理论基础上提出了更为方便适用的有限梁段法[4-5]。但以往的梁段有限元法往往只考虑一个剪力滞自由度,所采用荷载条件也大多为均布或竖向集中荷载,对于拥有复杂类型的荷载和边界条件薄壁梁,例如u′=0(u为剪切转角最大差值)等薄壁梁剪力滞效应问题无法满足其研究需求。基于此,Zhou[6]提出了每个节点两个剪力滞自由度的有限梁段方法,得到了考虑集中弯矩对箱梁剪力滞影响的梁单元系数矩阵和荷载列阵,为复杂桥梁的剪力滞效应研究提供了有效方法。目前,针对斜拉桥全桥的剪力滞效应分析大多是采用板壳(或实体)有限元方法对成桥状态下或部分特定施工阶段的结构进行静力分析[7-9],以获取主梁截面应力不均匀特征,进而判断剪力滞影响。这种方法不仅计算工作量大,而且不易直观反映施工过程中主梁荷载与剪力滞位移边界条件不断变化对截面应力不均匀现象(即剪力滞效应)的影响,也缺乏明确的物理意义。关于П形截面梁剪力滞效应的分析问题,已有方法:级数解法、翼板有效宽度的方法或者是基于板壳有限元模型的数值方法[10-11]。针对斜拉桥施工过程中结构、荷载与位移边界条件等不断动态变化的情形(除梁端节点外,其他节点按剪力滞自由度的约束情形可分边界简支、边界自由和内部节点,而边界自由和内部节点在施工过程中动态变化),周世军等[12]提出了一个能同时考虑结合梁剪力滞变形与弯曲变形耦合影响、适用于复杂荷载与边界条件的每节点两个剪力滞自由度的Π形结合梁单元,并对剪力滞效应对Π形结合梁斜拉桥主梁弯曲刚度的影响进行了详细研究。
笔者在文献[12]的基础上,改进了主梁截面翼板的纵向位移函数,导出了新的位移假定更为精细的结合梁单元刚度矩阵公式,在此基础上研究了文献[12]没有研究的П形结合梁斜拉桥主梁截面剪力滞系数随悬臂施工过程的动态变化规律。
1 基本假定
图1为钢-混凝土Π形结合梁主梁截面示意图。
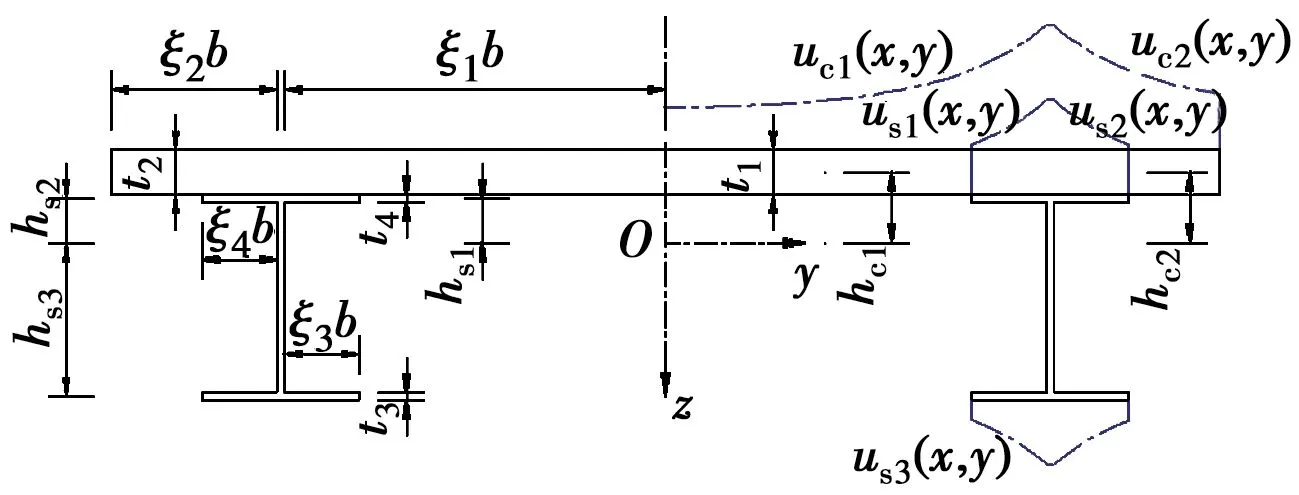
图1 Π形结合梁主梁截面示意图Fig.1 Cross section of Πshaped composite girder
与文献[12]简化的位移假定不同,假定混凝土和钢梁翼板纵向位移函数沿横向的每一段均为3次抛物线分布[2],钢梁上下翼缘采用对称位移函数,相同横坐标处混凝土桥面板与钢梁翼缘剪力滞曲线变化相似,腹板仍满足平截面假定;混凝土翼板、钢梁上下翼缘的板内竖向纤维无挤压,εz=0,板平面外剪切变形γxz、γyz以及横向弯曲、横向应变均可忽略不计;混凝土翼板与钢梁之间的滑移忽略不计。则可得到主梁的剪力滞翘曲位移函数
(1)
式中:w为竖向位移;ξib为工字钢腹板间净距的一半或混凝土及钢梁翼板悬臂宽度;hi为混凝土翼板和钢梁翼板到截面中性轴的距离;φ(x)为剪切转角最大差值;ζi为考虑翼板宽度和边界条件影响的修正系数,ζi=ηξi/ξmax,取值参照有限条法计算结果。
则混凝土翼板与钢梁上下翼缘的剪力滞位移函数分别为
(2)
式中:hc1、hc2分别为混凝土内、外翼板中轴距结合梁截面形心轴的距离;hs1、hs2分别为内、外钢梁上翼板中轴距结合梁截面形心轴的距离;hs3为钢梁下翼板中轴距结合梁截面形心轴的距离。
根据最小势能原理,体系总势能的一阶变分应该为零。
δΠ=δ(U+V)=0
(3)
式中:U为体系的形变势能;V为体系的荷载势能。
利用变分法,由式(1)~式(3)可得到关于φ(x)和w的微分方程和边界条件。
2 剪力滞理论公式
考虑剪力滞与弯曲变形耦合的具有两个剪力滞自由度的薄壁梁单元如文献[12]。按平面问题分析时,单元每节点共有5个单元力和单元位移分量;单元节点位移和单元节点力向量可以分别表示为

(4)
F=[NiQiMiSiTiNjQjMjSjTj]T
(5)
式中:S、T为广义剪力滞节点力,对应的φ、φ′为两个广义剪力滞位移自由度;其他节点位移和节点力分量的含义与一般梁单元相同。
选取与文献[12]相同单元位移模式,并应用最小势能原理,可得到与文献[12]表达形式相同的单元刚度矩阵公式(但由于剪力滞翘曲位移函数不同,公式内涵与文献[12]中的自然有所不同)。
K=Ke+Ks
(6)
式中:
(7)
Ke为基于初等梁理论的弹性刚度矩阵;Ks为剪力滞影响刚度矩阵,其包含了梁弯曲变形和剪力滞变形的耦合影响;K为考虑了剪力滞与弯曲耦合影响的Π形结合梁单元刚度矩阵;l为单元长度;I为关于z轴的惯性矩,I=Iw+Ifa(Iw为腹板对z轴的惯性矩)。根据剪力滞翘曲位移函数假定,截面相关惯性矩可以详细表示为
(8)
(9)
(10)
(11)
另外,剪力滞系数λ的定义与文献[6]相同。具体在腹板和翼板的交界处,剪力滞系数用λw表示;在翼板中点处,剪力滞系数用λc表示。
3 剪力滞效应施工动态过程分析
某双塔双索面Π形结合梁斜拉桥如图2所示[12]。对斜拉桥施工阶段Π形结合主梁截面应力分布规律进行了理论分析和实测验证。由于主桥结构基本对称,可以认为主梁截面剪力滞系数随施工过程的变化规律也基本对称,因此,重点介绍图2所示东索塔一侧1~9号主梁应力测试截面。测试截面上具体应力测点沿横向布置如图3所示。通过理论分析可以得到每一施工过程的主梁截面应力状态,以及任一施工阶段截面剪力滞系数分布规律。通过与实测应力的对比分析,验证方法的可靠性。

图2 应力测试截面位置示意图Fig.2 Stress measuring cross-sections in the bridge

图3 应力测试点横向布置图(单位:mm)Fig.3 Measuring points at cross section (unit: mm)
用新导出的结合梁单元对斜拉桥进行了按施工动态过程的有限元分析,得到Π形结合主梁截面应力受剪力滞效应影响随施工过程的变化规律。从全桥剪力滞分析角度出发,给出主梁部分施工阶段剪力滞系数理论值沿桥梁纵向(顺桥向)的分布情况,如图4~图8所示。图中λw为腹、翼交界处剪力滞系数,λc为顶板中心处剪力滞系数。另外,在图4~图8中,顺桥向坐标x表示主梁各截面到主桥左端边支座中心的距离。
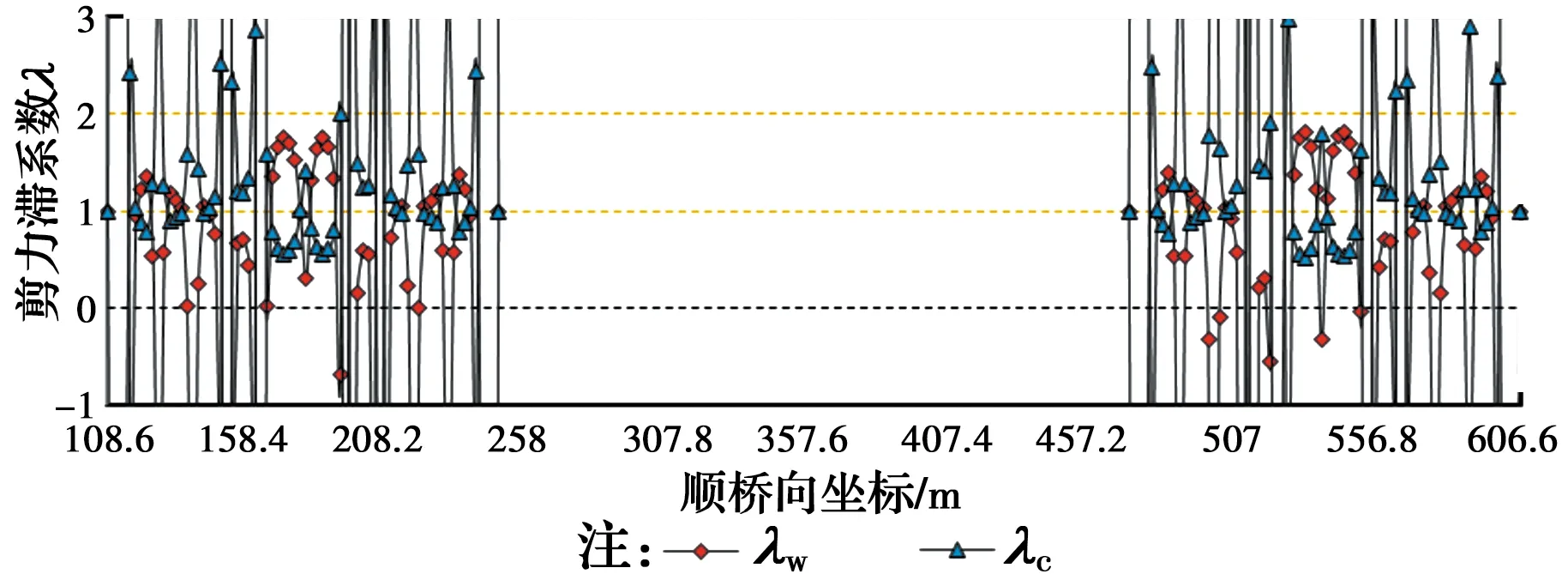
图4 5#索C1张拉后剪力滞系数λw/λc沿全桥的变化曲线Fig.4 Coefficients λw and λc after tensioning the cable 5#

图5 安装5#桥面板后剪力滞系数λw/λc沿全桥的变化曲线Fig.5 Coefficients λw and λc after the installation of deck 5#
从图4~图8可知,在不同施工阶段,主梁剪力滞系数的变化规律有明显不同,随荷载与位移边界条件变化,结合主梁顶板的剪力滞效应沿桥梁纵向呈“正负剪力滞”交替变化;在靠近桥塔区域,截面剪力滞系数变化愈加明显;与桥面板安装荷载相比,斜拉索张拉荷载对主梁剪力滞系数的影响更大,尤其在斜拉索锚头附近截面,剪力滞系数的变化更加剧烈,应予以特别关注。因此,以往研究成果中对斜拉桥剪力滞效应按静态结构进行分析具有明显的局限性,笔者按施工动态过程进行结合梁斜拉桥主梁剪力滞效应研究非常必要,其成果也具有独创性。

图6 12#索C1张拉后剪力滞系数λw/λc沿全桥的变化曲线Fig.6 Coefficients λw and λc after tensioning the cable 12#

图7 安装12#桥面板后剪力滞系数λw/λc沿全桥的变化曲线Fig.7 Coefficients λw and λc after the installation of deck 12#
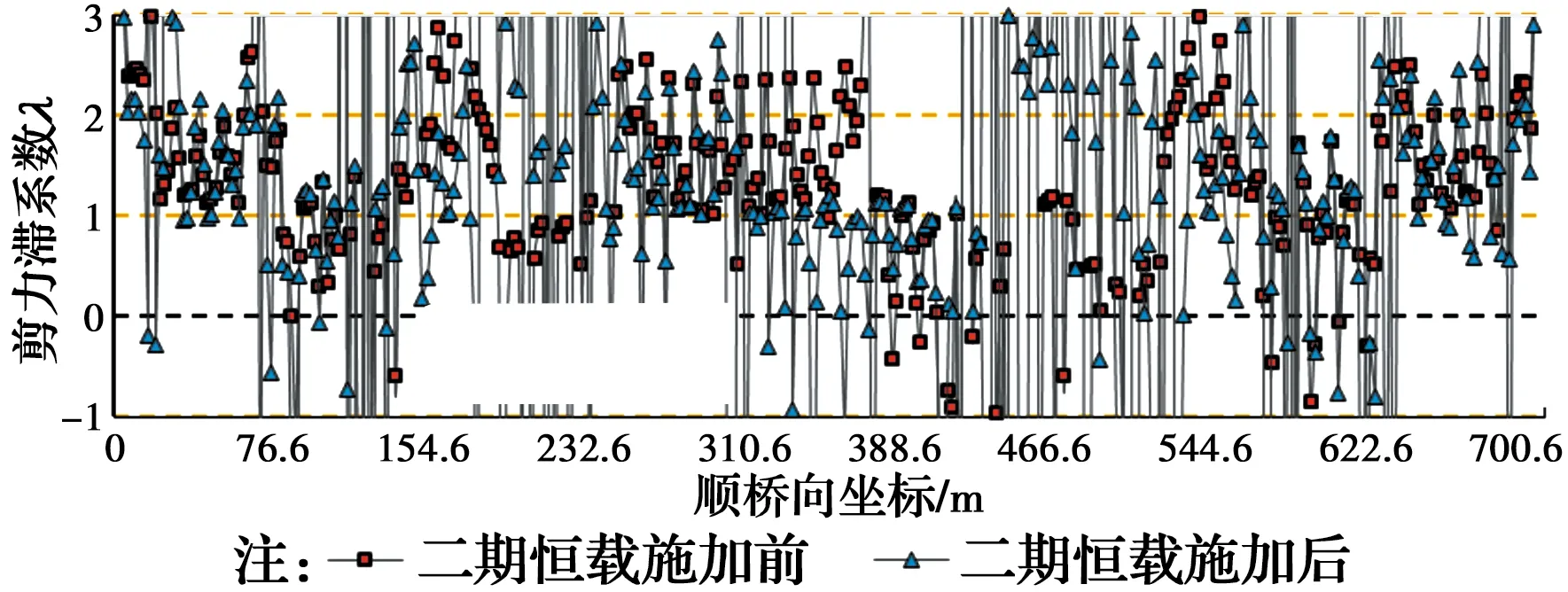
图8 二期恒载施加前后λw的对比图Fig.8 Comparison of λw before and after the secondary dead load
另外,从图4~图8还可以看出,在悬臂施工阶段,无论斜拉索张拉荷载,还是桥面板荷载,对主梁截面剪力滞系数的影响都比较明显,而成桥后的二期荷载的影响则相对较小。另外,在施工阶段,某一截面的剪力滞效应受施工阶段及不同工况的影响,可能呈现正负剪力滞效应交替的情形。
图9~图11为3个典型截面的剪力滞系数随施工状态变化的曲线。由图9~图11可以发现,在斜拉桥悬臂施工阶段,靠近桥塔梁段截面剪力滞效应突出,在远离桥塔区域,主梁截面剪力滞效应相对较弱;其中5#截面的剪力滞效应随施工过程呈正负剪力滞交替变化明显。
图12为8#截面在部分施工阶段的剪力滞系数理论值与实测值;图13和图14为3#截面在8号梁段施工阶段的理论值与实测值。由图12~图14可以看出,理论值与实测值吻合良好,表明提出的剪力滞效应计算方法结果可靠,能很好地反映施工过程中剪力滞效应对截面应力的影响。

图9 1#截面剪力滞系数随施工状态变化Fig.9 Variation of shear-lag coefficients at cross-section 1#

图10 5#截面剪力滞系数随施工状态变化Fig.10 Variation of shear-lag coefficients at cross-section 5#
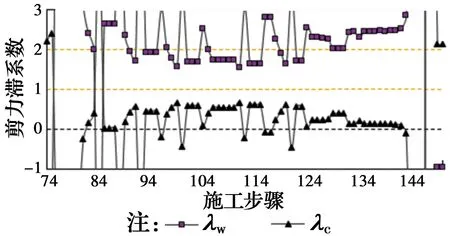
图11 9#截面剪力滞系数随施工状态变化Fig.11 Variation of shear-lag coefficients at cross-section 9#

图12 8#截面剪力滞系数理论与实测值Fig.12 Analytical and measured values of shear-lag coefficients at cross-section 8#
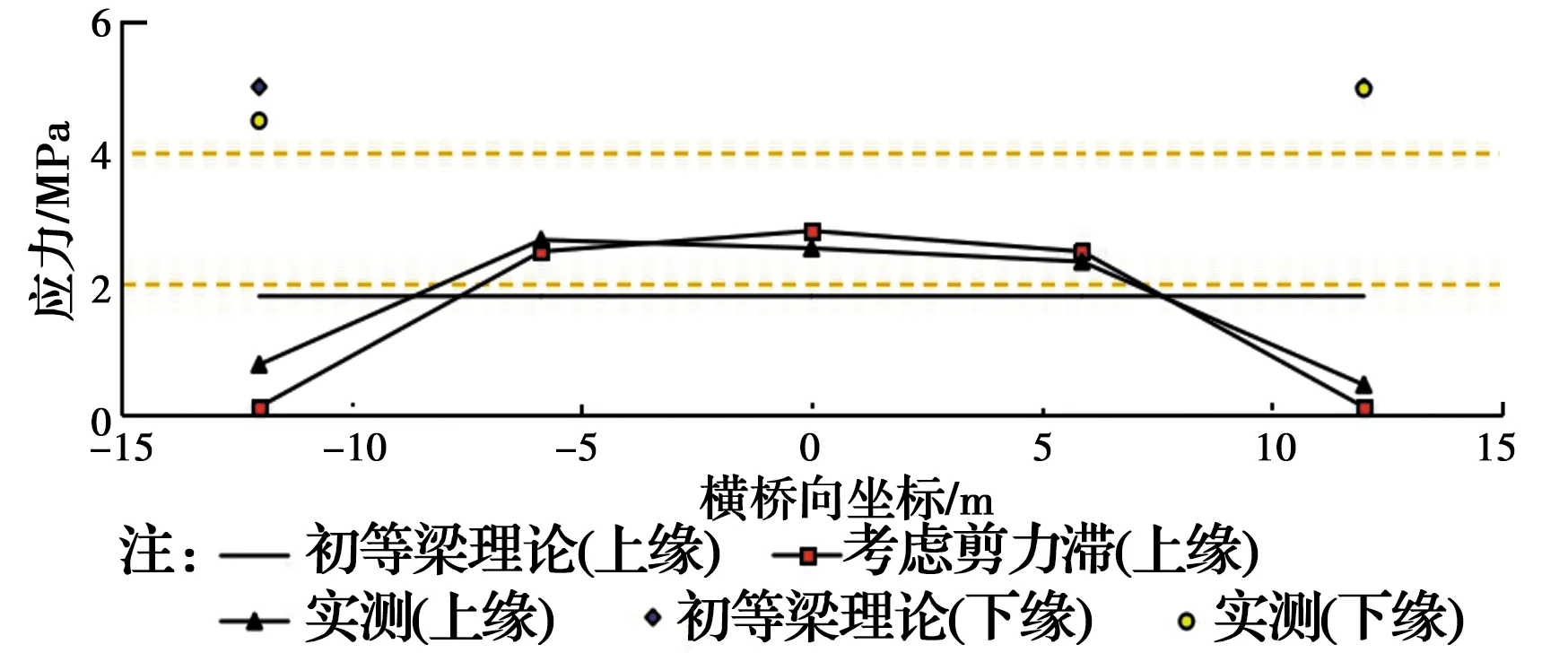
图13 8#索张拉后3#截面应力实测值Fig.13 Measured values at cross-section 3# after tensioning the cable 8#
图14 8#桥面板安装后3#截面应力实测值Fig.14 Measured values at cross-section 3# after the installation of deck 8#
4 结论
以Π形结合梁斜拉桥为背景,采用有限元方法对结合梁斜拉桥在悬臂施工阶段的剪力滞效应进行了分析,得到了结合梁主梁截面剪力滞系数随施工过程的动态变化规律,并与实测数据进行比较,得到了以下结论。
1)相较于剪力滞对Π形结合梁斜拉桥弯曲刚度的影响(中跨2%~7%,边跨3%~12%),结合梁主梁截面应力变化受到剪力滞效应影响要大很多(在施工过程中出现不少截面的λw大于2的情形),且在斜拉索主动张拉荷载作用下主梁剪力滞系数变化尤其明显;与成桥阶段相比,斜拉桥在悬臂施工阶段的剪力滞效应对主梁截面应力变化影响更大,应予以特别关注。
2)在悬臂施工过程中,随着施工各阶段荷载条件变化及相应的剪力滞位移边界条件的变化,斜拉桥主梁截面剪力滞效应沿桥梁纵向呈“正负剪力滞”交替变化。斜拉索张拉荷载会增大截面剪力滞效应,桥面板自重荷载则使主梁剪力滞变化相对减小。
3)靠近桥塔附近梁段截面与靠近悬臂前端梁段截面相比,其剪力滞效应在悬臂施工过程中更加明显;随着施工过程进行,主梁截面应力分布逐渐均匀,剪力滞系数变化逐渐减小。
4)斜拉桥部分主梁截面剪力滞系数过大可能是因为截面弯矩较小造成的截面应力数值较小而引起,即使计入剪力滞效应后,这些截面的应力水平也比较低。因此,在施工过程中更应该关注那些剪力滞系数较大且主梁弯矩绝对值较大的截面。
