基于贝叶斯修正IFAHP和灰色模糊综合评判的绝缘子污秽评估

黄 翔，王凌云，王 泉，邱 立*，李国平，董 宾

(1.三峡大学电气与新能源学院，宜昌 443002；2.国网湖北省电力有限公司秭归县供电公司，秭归 443600；3.国网江西省电力有限公司新余供电公司，新余 338025)

绝缘子作为电力输电线路中的重要设备之一，其污闪运行事故的频发严重影响着电网的安全稳定运行，给电力工业造成了巨大的电能损耗[1-2]。因此，准确有效地评估绝缘子污闪灾害风险，对于预防和降低输电线路故障概率、维护电力线路安全可靠运行具有重要意义[3-4]。

随着在线监测技术的发展，基于带电监测状态量对绝缘子污闪风险状态评估的研究已较为多见。文献[3-7]分别通过神经网络、随机森林、最小二乘支持向量机和模糊逻辑推理等算法对泄漏电流、污层电导率、紫外光斑面积和环境气象因子等特征参量进行处理，进而对绝缘子污秽状态进行诊断评价，但此类评估更侧重于污秽特征参数的人工取样测量和对盐密的关联拟合及预测等算法研究，不仅建模机理复杂、特征参数实时检测操作难度大，且试验样本依赖大量实验室测量数据，未能综合考虑到现场运行中绝缘子污闪状态参量的模糊不确定因素。文献[8]选取易于检测的紫外光脉冲信号，并结合运行年限和环境参数等建立了绝缘子状态综合评判模型，有效解决了污闪影响因素和评价过程模糊性的问题，为绝缘子状态评判提供了新思路。在此基础上，文献[9]以紫外脉冲数为主并对影响绝缘子污秽状态评估的指标体系进行扩充，提出了绝缘子状态模糊综合评估方法；文献[10]运用灰靶理论对绝缘子污秽状态等级进行划分，避免了在缺乏标准模式下难以进行综合评判的问题；文献[11]构建了熵权模糊综合评价模型，增强了绝缘子污闪评估的客观性，但与文献[8]同样存在赋权方法单一且只考虑到评价指标模糊性的不足；文献[12]利用云模型处理评判等级界限的模糊性和随机性因素，实现了分级区间的软化；文献[13]在云模型基础上将主客观权重相组合，综合考虑到绝缘子指标权值变化的时空特性。以上方法较好地体现了绝缘子状态评估的成果，然而均较少涉及指标信息获取不充裕而客观存在的“灰色”问题。

为综合考虑绝缘子污秽评估中指标类属划分不明的模糊性、客观条件不充分或偶然因素干扰的随机性影响和信息获取不全的灰性问题，基于贝叶斯修正的直觉模糊层次分析法(intuitionistic fuzzy analytic hierarchy process,IFAHP)，结合灰色模糊理论和灰云模型构建了绝缘子污秽状态的灰色模糊综合评判模型。针对现有灰色模糊评判模型的缺陷，创造性引进IFAHP和模糊熵理论确定评判因素权重集并采取贝叶斯修正法进行完善；同时利用灰云模型实现评判因素的模糊、随机性信息的定量集成转换，并以灰度表述其对应等级关系的可信程度，从而实现绝缘子污秽状态的综合评判。

1 灰色模糊理论基础

传统模糊综合评价有效改善了评价的模糊性问题，但未能考虑信息的不完全性，即灰性[14]。灰色模糊理论在模糊评价基础上引入点灰度(灰部)来刻画评判过程中参量信息的充裕程度，因而具有较好解决系统信息的模糊、灰色问题的能力[15]。

(1)

2 评判指标及权重集确定

2.1 评判因素及其权重集概述

绝缘子的污秽风险状态受众多因素综合作用的影响，参考文献[8，13]研究成果，构建紫外脉冲强度(X1)、运行年限(X2)、温度(X3)、湿度(X4)和气象条件(X5)五个指标作为绝缘子污秽状态的评判因素集。由于各因素之间的重要度不尽相同，故评判因素权重集的确定十分关键。

根据灰色模糊集理论，权重集应包括模部与灰部两部分，模部为指标权重值，反映各指标因素参与整体评判的程度，灰部则反映了模部信息的可信程度。然而当前灰色模糊评判模型[14-17]针对权重集的确定仍存在如下不足：①为充分体现出专家经验知识，这些研究通常采用应用广泛的AHP法确定指标权重。但AHP法中关于指标间重要程度的偏好信息不仅未能体现出决策者主观判断上的模糊性，更无法精确表达其对客观事物认知评价的弃权或犹疑情况，因而得到的权值较为主观、粗糙。②当前模型认为同级指标权值信息可靠度相差不大而将其对应的灰部取为一致相同，这显然忽略了指标重要度信息背后的灰性，使得权重集的确定欠缺科学合理性。

2.2 基于IFAHP和模糊熵的权重集确定

引进Xu[18]在保加利亚学者Atanassov的直觉模糊集理论基础上提出的IFAHP法来确定指标权值，以进一步提高评判模型权重集计算的精确性和适用性，具体步骤如下：

步骤1构造直觉模糊判断矩阵。请专家对同层指标两两比较，从而建立直觉模糊判断矩阵R=(rij)n×n=(μij,vij)n×n(i,j=1,2,…,n)。其中μij为隶属度，表示该专家认为指标i重要于指标j的偏好程度；vij为否定度，即指标j比i的重要程度，μij,vij∈[0,1]且μij+vij≤1；πij为专家的犹豫度或不确定程度，πij=1-μij-vij；n为该层指标个数。

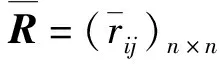
步骤3求取权重。对满足一致性的判断矩阵，由式(2)求得指标的直觉权重：

i,j=1,2,…,n

(2)

将直觉权重wi=(μi,vi)的隶属度μi归一化，即可作为常规权值进行模部运算，而否定度vi将纳入灰部运算处理。

步骤4确定权重集灰部。模糊集理论通常利用模糊熵来刻画集合的模糊不确定程度。为从整体上客观全面兼顾到指标判断信息，认为指标权值的可靠(可信)程度，即灰部应取决于其原始信息的可信程度，故引入直觉模糊熵公理[20]进行量化：

(3)

式(3)中：μi、vi分别为式(2)求得的指标i直觉权值信息的隶属度和否定度；Ei为指标i的直觉模糊熵，且数值越小则权值信息的不确定程度越小；oi为指标i权值对应的点灰度，为更好兼顾3.2节灰度评分标准界限，其值将由Ei经向量规范法处理得到。

2.3 基于贝叶斯优化模型的权重集修正

尽管IFAHP是一种更为精确完善的赋权新方法，但其本质上依然依赖于专家的经验知识。故而为进一步提高权重确定的客观性、充分考虑到指标实测数据，基于贝叶斯理论提出主观权重的优化模型来实现指标的二阶段赋权，以兼顾专家经验性和客观信息量因素。

根据概率论思想，专家主观权重可理解为先验概率，而某个待评样本下各指标权重可视为结合试验发生的概率(即后验概率)，因此可采用贝叶斯方法修正主观权重[21]。

p(Ai|Xj)=Gi,j,i=1,2,…,m

(4)

式(4)中：Gi,j为样本i下指标j的监测值；m为样本数量。

根据贝叶斯方法，在样本Ai下指标Xj的权重(后验概率)为

(5)

(6)

求解式(6)即可得到评判因素权重集的模部修正值。需要说明的是，由于指标监测值的不完全灰性已由3.2节确定的灰色模糊矩阵灰部体现出，故本文贝叶斯方法默认监测数据Gi,j真实可信，即权重集灰部不考虑修正。

3 判别矩阵的确定

3.1 基于灰云模型的评判集模部确定

当前综合评判模型通常采用人为经验确定的隶属函数来描述评判因素与类属等级的关联，以此得到的评判集模部不仅主观性大，且仅仅考虑了指标的模糊性，忽略了背后的随机性因素。王洪利等引入云理论，以一定范围内正态变化的随机数作为白化权值，提出了正态灰云白化权(简称灰云)模型的概念，从而既表达出系统信息的不完整、模糊性特点，又兼顾到人为主观判断的随机性因素影响[22]。因此文中采用灰云模型来确定绝缘子评估指标对应各类属等级的关联度作为评判集模部u，以实现评判中模糊随机信息与定常信息的不确切转换。

正态灰云的相应数字特征表示为(Cx,En,He)，具体含义及取值方法参见文献[22-23]。为便于表述，本文将左半边云和右半边云参数分别记为[(Cx,En,He);-]、[-;(Cx,En,He)]，再根据灰云参数确定出白化权函数[23]，便可求得评估指标i对各状态等级灰云的关联度。考虑到随机性因素影响，通常经多次运算求期望来确定最终计算结果。

3.2 评判集灰部及综合评判结果的确定

由于实际中收集的各待评样本数据充裕程度不尽相同，使得确定的模糊关系存在不可信度，若考虑其对整体评判结果的影响，需在评判集中引入灰部以表征模糊关系的可信水平。灰部取值由专家根据指标数据充裕程度进行打分确定，取值标准如表1所示[15]。

表1 灰度打分标准

(7)

式(7)中：wi、oi分别为指标i权重和对应的灰部；uik、oik分别为评判因素对第k个等级的灰云联系度及其对应点灰度；“∧”表示取极小值运算；k=1,2,…,f，其中f为等级数。

为统筹考虑到等级关联度及其灰度信息，采用内积法结合最大隶属度准则对评判结果综合处理。令bk=(uk,1-ok)，则最终评判等级通过计算bk范数大小确定[16]：

(8)

式(8)中：[bk,bk]表示向量bk的内积。

4 算例分析

为便于计算比较，选取文献[8]某一处污秽状态稍为严重的绝缘子数据(样本1)和文献[12]提供的某110 kV输电线路上5组绝缘子监测数据(样本2～样本6)进行评判分析，给出的指标归一化值见表2。参考电网设备状态评价实际规程并遵循文献[8-13]定义，将绝缘子污秽状态划分为注意、一般、较好、良好4个评判等级，以V1～V4依次表示。

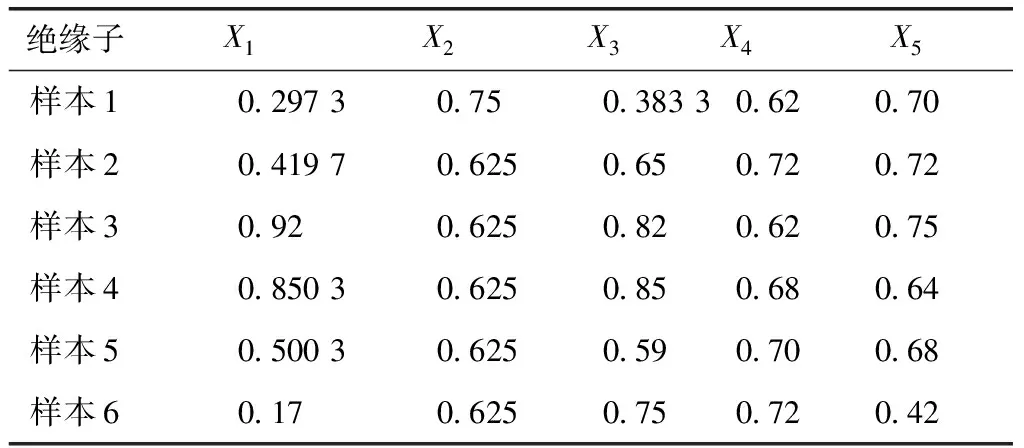
表2 绝缘子实测样本数据

4.1 评判因素权重集的确定

根据IFAHP法分析步骤，首先邀请相关专家参考0.1～0.9标度法给出各指标的直觉模糊比较矩阵如表3。

表3 各指标的直觉偏好关系

经一致性检验得一致性比率CR=0.139>0.1，于是采用文献[16]算法对原直觉偏好关系的判断矩阵参数进行调整(取迭代参数σ=0.8)，再将新判断矩阵构建为积型一致性矩阵进行检验(以上均在MATLAB中实现)，得到两矩阵距离测度值为0.049<0.1，即通过检验。于是将该矩阵代入式(2)得到评判指标的直觉权重向量W=[(0.796,0.681 6),(0.143 6,0.810 9),(0.082 8,0.883 9),(0.158 3,0.794 9)(0.124 2,0.828 7)]。

4.2 灰色模糊判别矩阵的确定

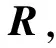
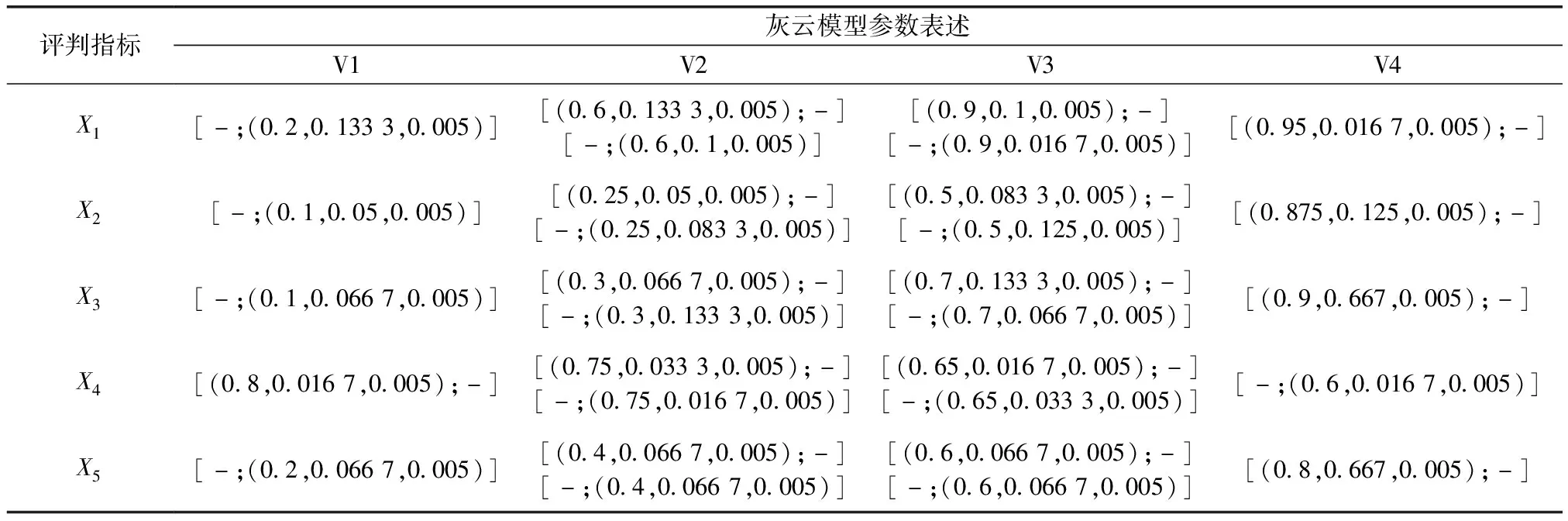
表4 绝缘子各评判指标状态分级的灰云模型

4.3 结果处理与分析

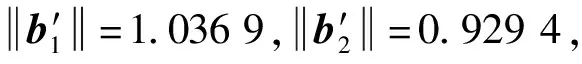
文献[8]和文献[12]分别采用模糊综合评判法、正态云模型对本例样本1进行了评估，结果对比见表5。同理，运用本文方法对绝缘子样本2～样本6综合评判的结果如表6所示，其中污秽情况为现场事后取样测得的等值盐密，与绝缘子的真实状态相对应。

表5 基于不同方法的样本1评估结果比较

表6 绝缘子样本2～样本6评估结果及对比

结合表5、表6比较结果可知，各种不同方法得到的评估结果基本一致，其中对于表6样本3，数据表明其各项指标均处于最优值附近，污秽情况轻微，即发生污闪事故可能性很小，故认为绝缘子运行状态良好，即V4等级更符合实际。以上初步说明了本文方法的有效性，且与以往方法相比，所提方法在合理处理评判因素的模糊随机性同时，可有效减小评估参量信息的灰色特性导致的结果偏差，进一步弥补了当前同类模型对于综合评价中不确切因素考虑的不足。

5 结论

针对绝缘子污秽评估中参量信息的多重不确切性，尝试结合灰色模糊理论和灰云模型提出了绝缘子状态的灰色模糊综合评判模型。模型首先提出采用IFAHP法确定评判因素权重，并引入直觉模糊熵公理量化表征权重的灰性，有效解决了当前灰色模糊评判法关于权重集确定不合理的问题；同时在此基础上，采用贝叶斯优化模型对权重集修正，既充分利用到原始数据蕴含的信息量，还克服了以往单一常权适应性差的缺陷，进而使得评判模型权重集的确定更为客观、完备。此外，利用灰云模型减少状态评判分级中的模糊性和随机性因素影响，实现了分级区间的软化，并以灰部兼顾参量信息的灰色特性，使得最终评估结果更为接近客观实际。实例表明，本文方法结论清晰、易于操作，但如何更好地考虑到指标间相互关系及单项指标的动态特性并完善指标体系，还有待进一步研究。