Effects of trapped electrons on the ion temperature gradient mode in tokamak plasmas with hollow density profiles
2020-06-14JingchunLI李景春JiaqiDONG董家齐andSongfenLIU刘松芬
Jingchun LI (李景春),Jiaqi DONG (董家齐) and Songfen LIU (刘松芬)
1 School of Physics,Nankai University,Tianjin 300071,People’s Republic of China
2 University of California,Irvine,CA 92697,United States of America
3 School of Physics and Optoelectronic Technology,Dalian University of Technology,Dalian 116024,People’s Republic of China
4 Southwestern Institute of Physics,Chengdu 610041,People’s Republic of China
Abstract
Keywords:micro-instabilities,trapped electrons,impurities
1.Introduction
In tokamaks,ion temperature gradient(ITG)driven instability is one of the drift waves and is considered a major factor for ion-scale turbulent transport.The ITG modes also have an important effect on the low(L)to high(H)confinement mode transition and energy confinement [1].The hollow (inverted)density profile occurs simultaneously with the pellet injection for plasma core fueling and L-H confinement transition[2–5].The study of drift wave instability under the hollow density profile and the turbulent transport caused by it can provide guidance for a pellet fueling experiment.Besides,it is well known that impurity ions are inevitably present in toroidal fusion plasma due to the inevitable interaction between the plasma and the first wall material.These impurity ions have significant effects on drift waves.Therefore,it is important to investigate the impurity ions effect on the ITG mode under a hollow density profile.
On the one hand,the ITG mode as well as the effect of impurities on it has been intensively studied theoretically and experimentally in the case of a monotonically decreasing density profile(R/Ln> 0)[6–8].The study of the ITG driven mode with impurities in toroidal plasmas was first investigated in[9].Later on,the effect of impurities on the ITG was also carried out in the reversed field pinch [10,11].On the other hand,in terms of the inverted density distribution(R/Ln<0),previous work on the ITG mode has not been systematic[12,13].Early theoretical studies include the calculations from Tang and Hahm [13,14].Their results showed that in the case of a negative density gradient,the ITG mode becomes unstable as the temperature gradient of ions exceed a certain critical threshold.Adam et al [15]demonstrated that the inverted density profile can cause particles to transport radially inward,which means,to some extent,that the profile is advantageous for fusion confinement.
Recently,studies relating to hollow density profiles have been carried out on many magnetic confinement fusion devices[16–21],such as the Mega Ampere Spherical Tokamak(MAST),Joint European Torus (JET),Axially Symmetric Divertor Experiment(ASDEX Upgrade),and the Large Helical Device (LHD).In addition,Tegnered et al [22]studied the transport of turbulent particles caused by ITG modes and trapped electron modes (TEM) under a hollow density distribution using the gyrokinetic code GENE and the Weiland Fluid Transport Model.It was found that the negative density gradient can suppress turbulence or change the relationship between diffusion and convection,and weaken the transport of particles to the core,thereby reducing the efficiency of fueling.Dong et al studied the electron temperature gradient (ETG)driven instabilities in plasmas with slightly inverted density profiles and demonstrated the E × B flow shear stabilization on the ETG modes,as well as on the transport[23].More recently,Du et al[24]used the local gyrokinetic eigenvalue code HD7[25,26]to simulate the ITG and TEM numerically under a hollow profile,and efficiently scanned the key parameters(i.e.,density gradient,temperature gradient,temperature ratios,and vertical wave numbers) affecting the ITG mode and TEM instability threshold and intensity.However,their research did not consider the effects of impurities.Impurities are inevitable in magnetic confinement fusion experiments,which not only cause a large amount of energy loss in the plasma,but also affect various instabilities in the plasma.They will in turn affect the distribution of the plasma parameters and confinement performance [27,28].
In this paper,we incorporate the trapped electrons (TEs)and impurities in the calculations,and systematically investigate the effects of TEs and impurities on the ITG modes in inverted density tokamak plasmas by adopting the gyrokinetic integral eigenmode scheme in a toroidal configuration.Our kinetic simulations found that in inverted density plasma,the increase of the ITG enhances the ITG growth rate and frequency.For the weak density gradient situation,the impurities(O+6)can decrease the growth rate as well as frequency of the ITG mode distinctly,and the greater the fraction of impurities,the greater the influence of inhibition of impurities on the the ITG mode.For the strong density gradient cases,impurities enhance the ITG instability,and the TE has a suppression effect on the modes.In addition,it is shown that the growth rate of the ITG decreases with the increase of positive magnetic shear s,while the real frequency increases with the increase of positive magnetic shear s.Furthermore,the growth rate of the ITG enhances while the real frequency decreases with the decrease of negative magnetic shear s.The relationship between the ITG mode and magnetic shear is emphasized for both slight and strong hollow density profiles in tokamak plasmas.
The remainder of this paper is organized as follows.The gyrokinetic equation and physical model are introduced in section 2.The numerical results of the ITG modes in an inverted density plasma edge with impurities are presented and analyzed in section 3.Finally,a brief conclusion is presented in section 4.
2.Physical model
To begin with,to make the structure of the article more complete,we first present the local gyrokinetic integral scheme used in this paper.We use the ballooning mode representation to study the ion-scale drift wave instability in tokamak plasma,with the linear mode coupling caused by the configuration of the toroidal magnetic field taken into account.The main ions in the system are hydrogen ions,and different ionized states of lithium,carbon,oxygen,nickel,tungsten,etc.are impurity ions.The main ions and impurity ions are all passing particles,which are described by a gyrokinetic model.In a toroidal geometry system with circular cross-sections,we consider the full kinetic effects of the main and impurity ions,such as magnetic field curvature and gradient drifts,finite Larmor radius (FLR) effects,and wave-particle resonance effects.Here,we ignore the FLR effect of the TEs and believe that the passing electrons are subject to adiabatic response.
When considering the effects of TEs and impurity ions,low-frequency electrostatic disturbances in non-uniform plasmas can be described by quasi-neutral conditions:
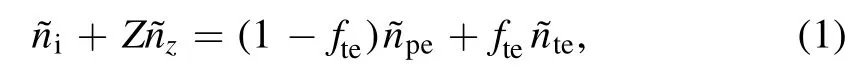
In the ballooning representation and with the gyrokinetic equation,the non-adiabatic response of the particle is governed by:
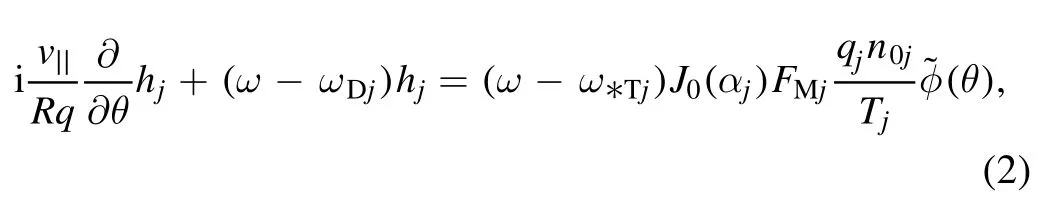
where the magnetic(gradient and curvature)drift frequency is
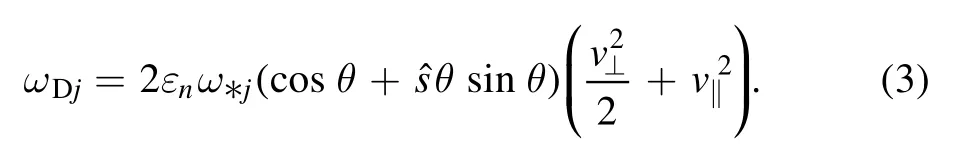
The diamagnetic drift frequency induced by the pressure gradient is:

The definitions of the other parameters are as follows.The transit frequency isωt=v‖Rq,and the electron diamagnetic drift frequency isω*e=ck θTeeBLne,vtj=The non-adiabatic response of the TEs can be achieved by expanding equation(3)withω/ωbe,whereωbeis the bouncing frequency of the TEs.When ignoring the FLR of the TEs,the density perturbation of the TEs can be expressed as
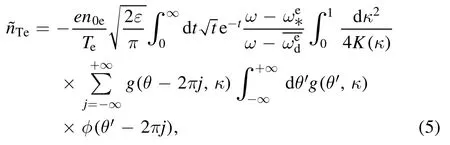
The precession drift frequency of the TEs is written as
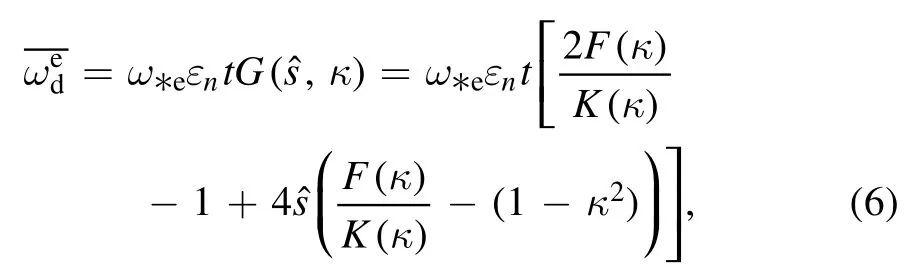
After complex mathematical operations,we obtain the expression of the integral eigenequation corresponding to equation (1):
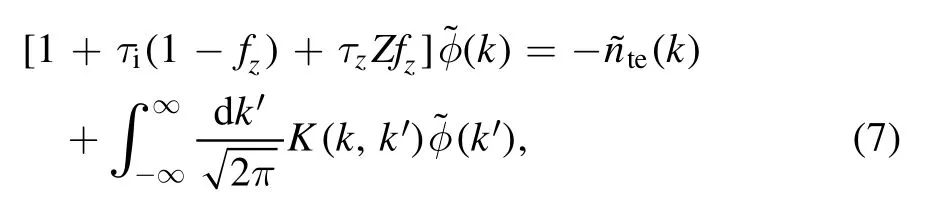
where
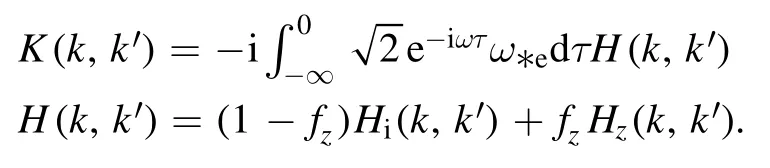
The equation contains two types of ions,one is hydrogen ion,which are the main ion in the plasma,and the other is called impurity ion because of their small fraction.Among them
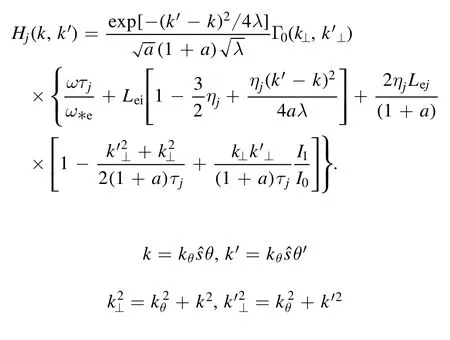
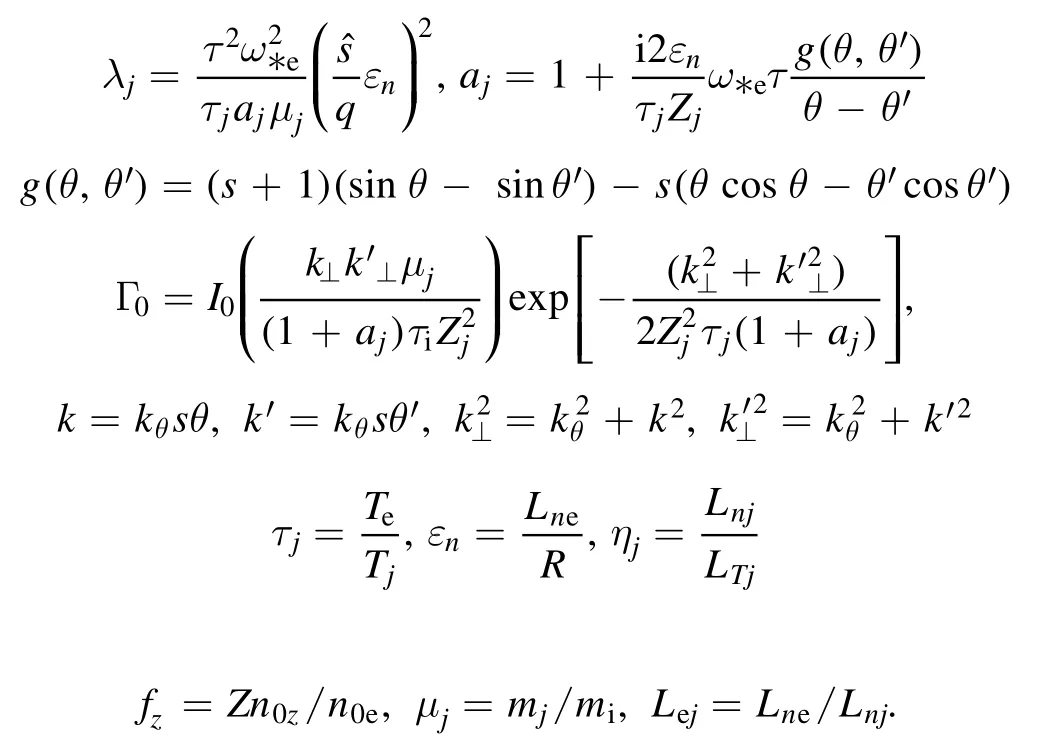
Herek,k',kθis normalized to=Ωi/vti=andIl(l=0,1)is the modifeid l-order Bessel function.All symbols have their general meaning,such as the density gradient scale lengthLnj=-nj/∇nj,undisturbed plasma density n0,temperature gradient scale lengthLTj=-Tj/∇Tj,safety factor q,and magnetic shears=rdq/qdr.Z is the ion charge number,mjandTjare ion mass and temperature,and R is the major radius of the torus.It should be noted that not all parameters are independent,for example,based on quasi-neutral conditions,
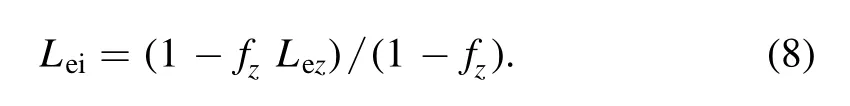
While assumingTi(r)=Tz(r),we achieve
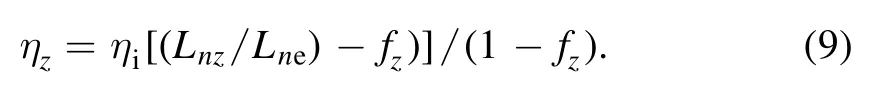
The parametersηi,ηe,εnand other parameters in the equation will influence the dispersion relationship.We use the gyrokinetic integral code HD7 to discuss their effects in the next section.
3.Numerical results and analysis
We now study the effect of impurity on the ITG mode with different temperatures and density gradients with the gyrokinetic integral eigenvalue code HD7.Compared with the nonlinear simulation,the limitation of linear simulation here is that the turbulence saturation amplitude cannot be obtained,and the relationship between microscopic instability and turbulence cannot be studied.However,linear simulation is still necessary:(i)it can determine the possible driving mechanism and instability conditions;(ii) when the transport caused by turbulence dominates,the plasma density and temperature gradient may be adjusted to be close to the threshold predicted by the linear instability theory;(iii) the temporal and spatial characteristics of the linear mode may be related to the turbulent flow,which can provide a rough estimate of the turbulent transport.We investigate the influence of other parameters like impurity species and magnetic shear on the ITG instabilities.In our calculations,since we consider hollow density profile plasma,Lez=Lne/Lnz> 0 means that the density gradients of the impurity and main ions are in the same direction,namely,impurities are peaked toward the plasma edge.Lez< 0 means that the density gradients are in opposite directions.
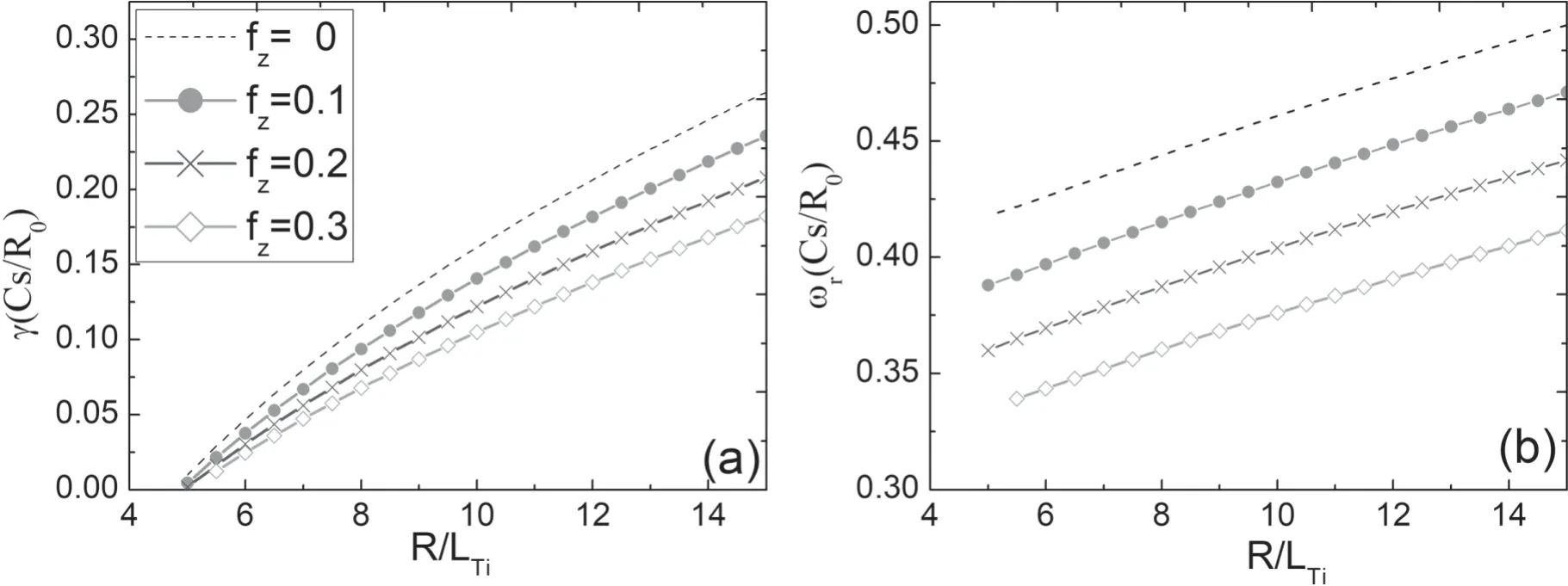
Figure 1.Normalized growth rate (γ) and real frequency (ωr) of the ITG versus R/LTi for different impurity charge concentrations fz.The other parameters are s=0.8,q=1.4,kθρs=0.4,Lez=2,ηe=1,and R/Lne=–1.O+6 is treated as impurities.

Figure 2.Normalized growth rate (γ) and real frequency (ωr) of the ITG versus R/LTi for different impurity charge concentrations fz.The other parameters are s=0.8,q=1.4,kθρs=0.6,Lez=2,ηe=1,and R/Lne=–8.O+6 is treated as impurities.
3.1.Dependence on the ITG
The normalized growth rate(γ)and the real frequency(ωr)of pure ITG modes versus R/LTiare presented in figures 1(a)and (b),respectively,where the length of the normalized electron temperature gradient scale R/LTeis equal to the length of the electron density gradient scale R/Lne.It must be explained here that the black dotted line represents the result of no impurities,i.e.,fz=0.We can see that the increase of the ITG enhances both the growth rate and frequency of the ITG modes,and impurities decrease the growth rate as well as frequency of the ITG mode distinctly.The higher the fraction of impurity O+6,the greater the suppression effect of the ITG.This suggests that the ITG modes are damped by impurity ions.The stabilizing effect of impurities is consistent with previous research results,because when the gradient of the impurity ions is the same as the electron density gradient,the dominant ion density is diluted (the relationship between the ion density gradient and the fraction of impurities is presented by equation(8))[28–32],which makes the impurity ion effect weaken the driving force of the ITG and stabilizes the ITG mode.
Figure 2 is the same as figure 1 except that it has a strong density gradientLne=-ne/∇ne=–8.Compared with figure 1,the real frequency of the ITG in figure 2 is lower.Most importantly,the impurity increases the growth rate of the ITG mode,which is very different in the weak density gradient case.For the strong density gradient,we have to consider the gradient of the main ion density.We have Lez=Lne/Lnzand Lei=Lne/Lni.Since Lezis positive while Lneis negative,this leads to the gradient of the impurity ion density being the same as that of the main ion density,which increases the ion density gradient and enhances the driving force.Therefore,the effect of impurities is destabilizing.
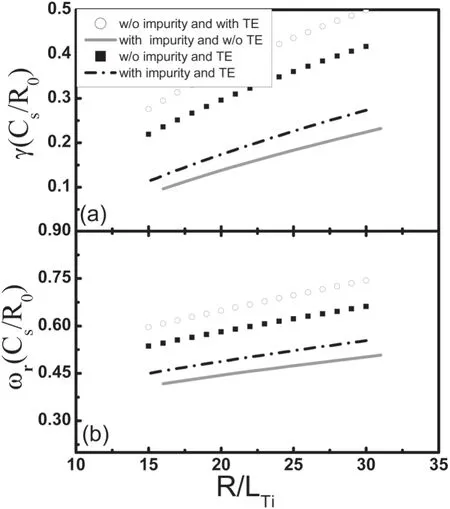
Figure 3.Normalized growth rate (γ) and real frequency (ωr)versus R/LTi for different cases.The other parameters are s=0.8,q=1.4,kθρs=0.6,and R/Lne=–1.O+6 (with fz=0.25) is treated as impurities when they are incorporated.
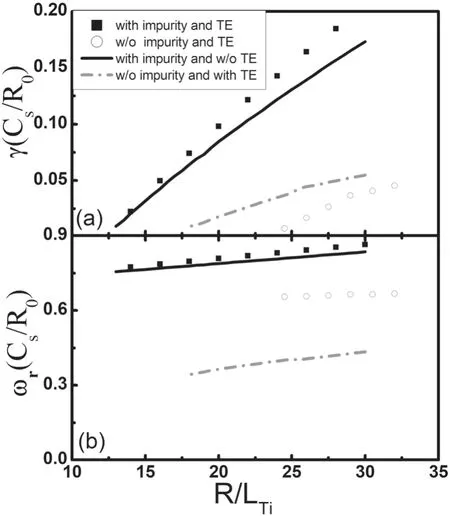
Figure 4.Normalized growth rate (γ) and real frequency (ωr)versus R/LTi for different cases.The other parameters are s=0.8,q=1.4,kθρs=0.6,and R/Lne=–8.O+6 (with fz=0.25) is treated as impurities when they are incorporated.
3.2.Effect of TEs
Figure 3 shows the normalized growth rate (γ) and real frequency(ωr)versus R/LTifor different cases,namely,with and without impurities,TEs.We set other parameters as:s=0.8,q=1.4,kθρs=0.6,and R/Lne=–1.As can be seen from figure 3,the impurity has a stabilizing effect on the ITG,and the TE can enhance the ITG instability,where the stabilization effect of the impurities is consistent with the previous simulation results.Concerning the destabilizing effect of TE,usually,when there are TEs,free energy is transferred from the TEs to the waves due to the precession drift resonance,so the TEs are destabilizing for the ITG.This resonance with TEs is related to the bounce average precession frequency(see equation (5)).The direction of the precession is in the toroidal direction.In fact,the resonance of TEs with the ITG mode is clearly represented by the denominator in the front of the integration overκd2in equation (5),which indicates that the resonance occurs between the mode oscillation(ω)and the bounce averaged precessional motionof TEs in the toroidal direction.Such resonance may have a destabilizing effect on the mode.
The normalized growth rate (γ) and real frequency (ωr)versus R/LTifor different cases,namely,with and without impurities,TEs are presented in figure 4 with R/Lne=–8.The other parameters are the same as those shown in figure 3.We can see that there is a big difference between the TE effects between the weak and strong density gradient cases.In the weak density gradient situation,the TE effects tend to enhance the ITG instability,while the impurity has a clear stabilizing effect.However,in the strong density gradient cases,both the effects of impurities and TEs increase the ITG instability,especially the role of impurities,which makes the growth rate of instability increase by a large amplitude.This result in the hollow density profile plasma is exactly the opposite of that in plasmas with normal density gradient.We need to note that,generally speaking,for the former case,the total effect of TEs and impurity ions is stabilizing,while for the latter cases,the total effect is destabilizing.
3.3.Effect of magnetic shear
Numerous studies have shown that magnetic shear is an important parameter affecting instability,turbulent transport bifurcation,ion temperature profile invariance,and turbulent spreading.This is mainly because magnetic shear can affect the radial structure of the drift mode.In some experimental devices,the core weak magnetic shear discharge mode,which is listed as one of the candidates for the advanced operating modes of ITER,is studied.In this mode,the safety factor profile of the core is relatively flat and the magnetic shear is relatively small.A large number of studies have shown that the weak magnetic shear discharge pattern can well suppress the current-driven and fast MHD instability,but it is found that some slow-growing modes still grow,including microscopic drift instability.
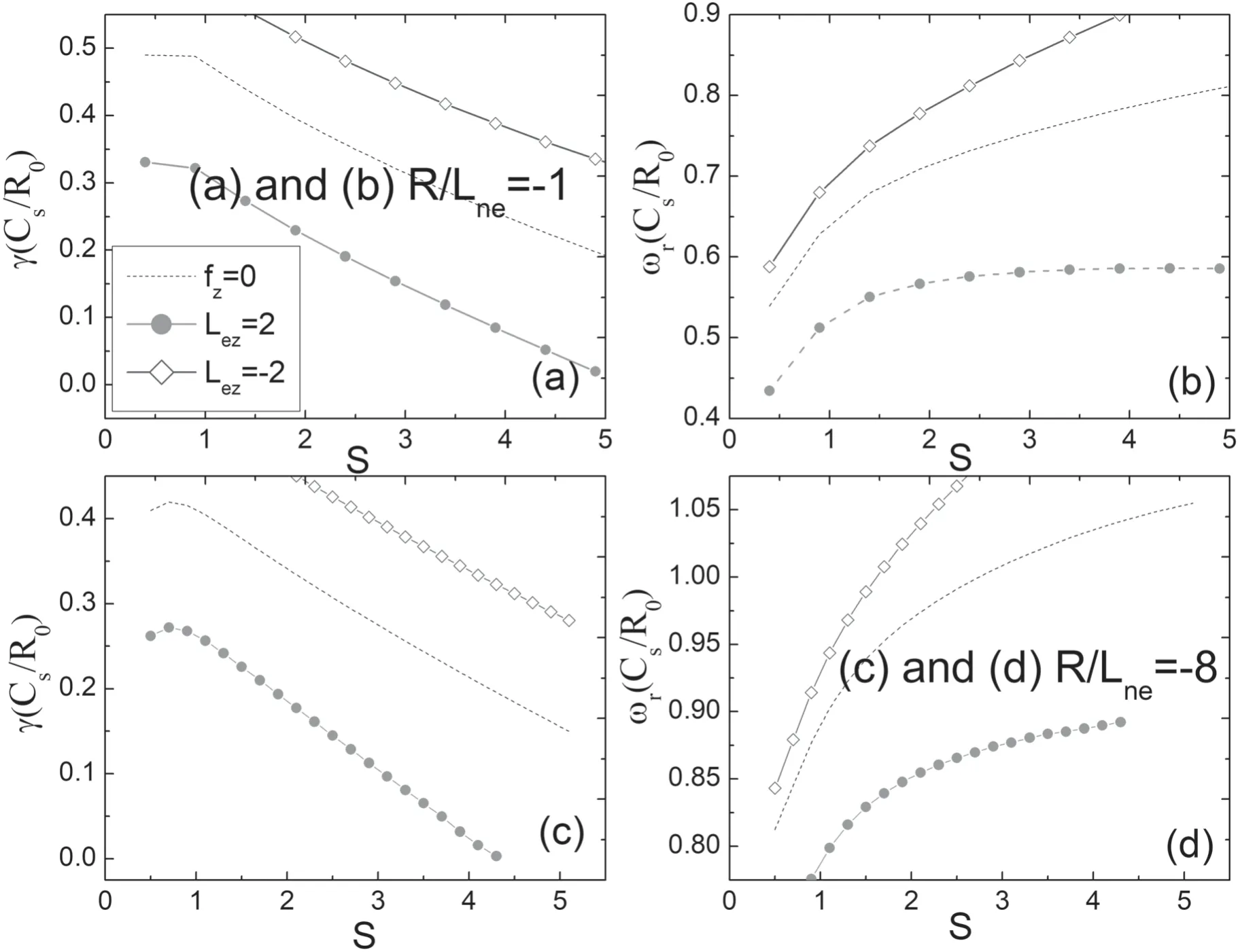
Figure 5.Normalized growth rate(γ)and real frequency(ωr)versus positive s with different Lez.(a)and(b)represent R/Lne=-1;(c)and(d) represents R/Lne=-8.Other parameters are set as:s=0.8,q=1.4,kθρs=0.4,and ηe=1.C+6 (fz=0.2) is treated as impurities.
In this subsection,we investigate the effect of magnetic shear on ITG instability in inverted density plasma.For comparison,we chose R/Lne=–1 and R/Lne=–8,respectively,to compare the flat and steep electron density distributions to analyze the influences of magnetic shear on ITG instability.Figure 5 depicts the normalized growth rate (γ)and real frequency (ωr) versus positive magnetic shear s with different Lez.Figures 5(a) and (b) represent R/Lne=–1;figures 5(c) and (d) represent R/Lne=–8.We set the other parameters as:s=0.8,q=1.4,kθρs=0.4,and ηe=1.C+6is treated as impurities.From figure 5,it is shown that the growth rate of the ITG mode decreases with positive magnetic shear s while the real frequency increases with positive magnetic shear.That means,large magnetic shear will suppress the growth of the ITG mode.A strong electron density gradient only changes the real frequency of the ITG mode,while it hardly affects the relationship between the ITG mode and the magnetic shear.
Figure 6 is the same as figure 5,except the magnetic shear is negative.From figure 6,we can see that the growth rate of the ITG increases with negative magnetic shear s while the real frequency decreases with the decrease of negative magnetic shear.This indicates that the ITG mode will also be suppressed with larger negative magnetic shear s.It should be noted that under the steep electron density distribution,the effects of impurities on the ITG shown in figures 2 and 5 are different.This is because we do not consider TEs in figure 2,and in figure 5 we do consider TEs.If figure 5 does not incorporate TEs,figures 2 and 5 are consistent under a negative strong density gradient.
3.4.Eigenmode structure
In this subsection,we discuss the eigenmode structure of the ITG modes in the ballooning space.To compare the results,we use s=0.9 and s=–0.9 to discuss the characteristics of the ITG in the negative and positive magnetic shear intervals,respectively.The red solid line and the blue dashed line represent the real partand the imaginary partof the disturbing electrostatic potential,respectively,in figure 7,which shows the eigenmode structures of the ITG in θ-space with s=0.9.Figures 7(a)–(c) represent R/Lne=–1 and figures 7(d)–(f) represent R/Lne=–8.Other parameters are set the same as those in figure 5.Figure 8 is the same except s=–0.9.For positive s,we can see that the eigenmode structure is well localized in the ballooning space.For negative s,the eigenmode is elongated along the direction of the magnetic field lines,thus requiring a higher calculation accuracy.As shown in figures 7 and 8,the length calculated in the negative s interval is greater than the value in the positive s.In addition,we learn that for relatively large electron density gradients,the ITG mode structure has oscillations in the θ-space.
4.Summary and discussion
In this paper,with a local equilibrium model,the local properties of the ITG mode in tokamak plasmas of inverted density profiles are studied in the presence of impurity ions and TEs,using the gyrokinetic integral eigenvalue code HD7.The specific results obtained can be summarized as follows.
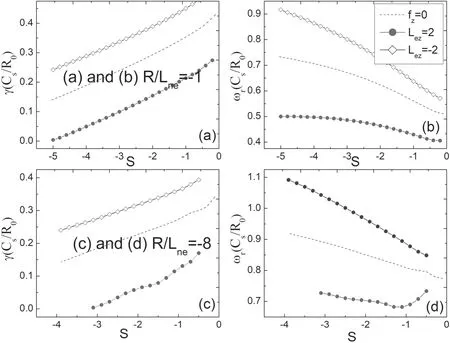
Figure 6.Normalized growth rate(γ)and real frequency (ωr)versus negative s with different Lez.(a)and(b)represent R/Lne=–1;(c)and(d) represent R/Lne=–8.Other parameters are set as:s=0.8,q=1.4,kθρs=0.4,and ηe=1.Fully ionized carbon (C+6,fz=0.2) is treated as impurity species.
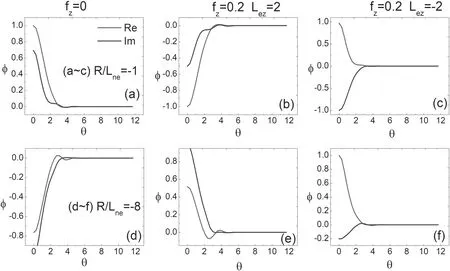
Figure 7.Eigenmode structures of the ITG in the(θ)space with s=0.9.(a)–(c)represent R/Lne=–1;(d)–(f)represent R/Lne=–8.Other parameters are set the same as those shown in figure 5.C+6 is treated as impurities with fz=0.2.
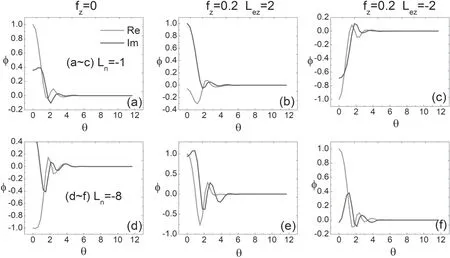
Figure 8.Eigenmode structures of the ITG in the(θ)space with s=–0.9.(a)–(c)represent R/Lne=–1;(d)–(f)represent R/Lne=–8.Other parameters are set the same as those shown in figure 6.C+6 is treated as impurities with fz=0.2.
(1) The increase of the ITG enhances the ITG growth rate and frequency.The effects of the TEs and impurity ions depend on the electron density gradient.In the weak density gradient situation,the TE effects tend to increase the ITG instability,while the impurity has a distinct stabilizing effect.However,in the strong density gradient cases,both the impurity and TEs increase the ITG instabilities.
(2) The magnetic shear s is an important parameter affecting ITG instability.It is found that the growth rate of the ITG decreases with positive magnetic shear s while the real frequency increases with s.We also demonstrate that the growth rate of the ITG increases with negative s while the real frequency decreases with s.In addition,in inverted density plasma,the length of the calculated mode structure in the negative s interval is greater than that in the positive s case.
Future work will include a quasi-linear study of TE and impurities effects on the ITG mode in toroidal plasmas with hollow density profiles.Moreover,electromagnetic simulations of the ITG in toroidal plasmas are also ongoing.
Acknowledgments
The authors would like to thank Huarong Du and Jia Li for fruitful discussions.This work is supported by the National Key R&D Program of China (Nos.2018YFE0303102 and 2017YFE0301702),US SciDAC GSEP,the NSFC (Nos.11905109 and 11947238),the China Postdoctoral Science Foundation (No.2018M640230),and the Fundamental Research Funds for the Central Universities,Nankai University (63191351).
猜你喜欢
杂志排行
Plasma Science and Technology的其它文章
- Vickers hardness change of the Chinese low-activation ferritic/martensitic steel CLF-1 irradiated with high-energy heavy ions
- Comparison of discharge characteristics and methylene blue degradation through a direct-current excited plasma jet with air and oxygen used as working gases
- Evaluation of influence of cold atmospheric pressure argon plasma operating parameters on degradation of aqueous solution of Reactive Blue 198 (RB-198)
- Plasma-induced graft polymerization on the surface of aramid fabrics with improved omniphobicity and washing durability
- Plasma-assisted abatement of SF6 in a packed bed plasma reactor:understanding the effect of gas composition
- The far-field plasma characterization in a 600W Hall thruster plume by laser-induced fluorescence
