融合遗传算法与改进响应面技术的混凝土热学参数反分析

何 伟，袁亚芳，白 冰，王 湘

(华北水利水电大学土木与交通学院，河南 郑州 450045)

0 引 言

倒虹吸、渡槽是常见的水工建筑物，属于大体积混凝土结构。混凝土收缩、结构不均匀沉降、内外温差等都会导致裂缝产生，因而大体积混凝土防裂问题一直是工程难题。近年来，一些学者应用数值模拟技术仿真分析混凝土施工以预防混凝土开裂。混凝土热学参数与施工仿真分析结果精度密切相关，常取规范值或通过实验室测定。采用规范值的数值计算结果与工程实测值之间往往误差较大；而试验测定主要通过现场取样，室内实验得到。实验时由于试样受力状态与环境发生了改变，因而往往难以得到真实参数值[1-2]。大体积混凝土施工中常布有多种传感器，以量测混凝土浇筑过程中温度变化。如果依据实测温度值建立数值模型，对当前热力学参数进行反分析，则反演得到的参数值将更符合其实际工况。

目前用于参数反分析的方法主要有响应面法、最小二乘法、遗传算法等。响应面法最初由Box和Wilson[3]于1951年提出，该方法可靠性高、操作性强，但传统响应面法在构造响应面函数时未考虑各参数物理意义及区间差异的问题，因此存在稳定性较差且物理性质不明确的问题。Das等[4]提出运用含交叉项二次多项式代替不含交叉项的二次多项式拟合响应面模型，使数值模型的计算精度大幅提高。陈立波等[5]利用Plackett-Burman 试验方法设计参数样本，提出了改进的响应面法，与传统响应面法计算结果比较，计算效率和精度均明显提高。为解决非线性优化的问题，郭利霞等[6]利用遗传算法对混凝土湿度场的特征参数进行反分析，仿真计算值和实测值的湿度变化规律基本一致，且遗传算法参数寻优精度高，收敛速度快。因此，如何高效、准确地反分析混凝土热力学参数是值得研究的。

本文提出了一种融合遗传算法与改进响应面技术的参数反分析方法，在混凝土热学参数灵敏度分析的基础上，建立混凝土物理参数与温度关系改进响应面模型，根据最小二乘原理构造反分析目标函数，并基于遗传算法程序搜寻最优参数组合。以南水北调工程中线某段倒虹吸现场施工实测温度值反演分析混凝土热学参数，验证该方法的可行性。

1 改进的响应面技术

响应面法主要是利用非线性数值模型来描述试验变量和响应量之间的隐式函数关系，包括试验设计、响应面的拟合和优化分析3个步骤[7]。常选取多项式函数作为响应面数值模型，含交叉项的二次多项式响应面模型形式如下

(1)

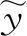
传统响应面法拟合不同数量级与量纲的参数因子和响应量，物理意义不明确，且数量级间差异对拟合结果造成较大的误差。为了统一各参数量纲，避免数据拟合时大参数淹没小参数，提高计算效率和结果精度。对响应面法进行改进，分别以各参数规范值为中心，确定待拟合参数区间为±35%，均一化处理各参数值和响应值[8]，使各参数值和响应值都严格映射到区间[-1，1]，转换函数如下

(2)

式中，X′、X、Xmid、Xmax、Xmin分别为均一化后的响应值或参数值、响应值或参数值、响应值或参数中值、最大响应值或参数值、最小响应值或参数值。

将式(2)代入式(1)，得改进的响应面模型

(3)

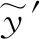
2 融合遗传算法与改进响应面技术参数反分析法

遗传算法(Genetic Alg orithm，GA)是借鉴生物界进化规律演变而来的一种全局搜索方法[9-10]。遗传算法在进化搜索中基本不利用外部信息，仅以适应度函数为依据，利用种群中每个个体的适应度值进行搜索，适应度值与遗传到下一代的概率成正比关系。适应度函数为

(4)

式中，F(x1，x2，…，xn)为适应度函数；x1，x2，…，xn为种群个体；fi(x1，x2，…，xn)为待分析问题的数值模型计算值；Ci为数值模型计算值对应的实测值。

为了快速找到满足模型精度要求的优化值，避免寻优不收敛，约束函数如下

(5)

式中，ε为待优化问题的精度。

为了克服响应面法效率低和遗传算法参数反分析易寻优失败的问题，提出一种新的融合改进的响应面技术与遗传算法得参数反分析方法:

(1)建立结构数值模型。

(2)确定待反分析参数个数及其变化范围并采用CCD法设计试验参数。

(3)利用数值模型计算响应值。

(4)利用式(2)将上述参数值与响应值作归一化处理，映射到区间[-1，1]，代入式(3)构建改进的响应面模型。

(5)利用改进的响应面模型，建立反分析目标函数如下

(6)

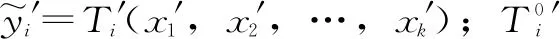
(6)参数寻优。依据式(4)、(6)构造遗传算法的适应度函数，根据精度要求及式(5)确定参数寻优约束条件。运用遗传算法的选择、交叉、变异操作算子在[-1，1]区间内优化计算，找到满足精度要求的最小适应度函数值，输出最优参数组合，程序运行终止。

图2 测温计布置

3 工程实例

3.1 工程概况

某倒虹吸总长275.0 m，其中管身水平投影为116.0 m。管身横向为3孔1联的箱形钢筋混凝土结构，单孔孔径7.1 m×7.1 m(宽×高)；总尺寸为25.1 m×9.3 m(宽×高)；管身采用C30混凝土。工程施工分三层浇筑成型。第一层(底板)浇筑养护历经58 d；第二层(竖墙)第59 d开始浇筑，历经10 d；第三层(顶板)第69 d开始浇筑养护。从第一层至第三层的浇筑、养护和最终成型共历经103 d。利用ANSYS软件建立倒虹吸水平段三维有限元模型，选用SOLID70单元定义材料，共划分52 488个单元，结构的三维有限元模型如图1所示。

图1 结构三维有限元模型

采用ANSYS软件的热分析模块模拟计算，混凝土入模温度为10℃，考虑结构表面与环境温度间热量传递，为第三类边界条件；结构内部的热源主要是水泥水化热。混凝土热学参数按规范取值。为比较模型计算值与其实测值间的差异，施工时在倒虹吸底板跨中断面布置有测温计，测点位置如图2所示。

当有限元模型中混凝土材料属性采用规范值计算倒虹吸施工温度场时，测点S9温度计算值和实测值具有较大的误差，表明混凝土热学参数实际值与规范值相差较大，因此需要对混凝土的热学参数进行反分析。

3.2 参数灵敏度分析

灵敏度分析主要是研究系统影响因子在微小摄动时系统的变异情况，定量分析各影响因子对系统的贡献[11-12]。混凝土温度场受热学参数、水化热、气温及养护条件等因素的影响。根据热传导方程[13-14]基本理论，为剔除对温度变化影响不显著的因素，对混凝土施工过程中的温度变化有影响的比热容、导热系数、热交换系数及混凝土的水化热进行参数灵敏度分析，灵敏度定义[15]如下

T=T0+S(X1-X0)

(7)

T为未知或为离散函数时，响应温度T对各热学参数Xi的灵敏度S(T/Xi)为

(8)

式中，当i=1，2，3，4时，Xi分别为热力学参数c、λ、β、Q0；X0i为初值X0中的第i个参数。

以热学参数规范值为中心，在各参数±20%范围内以步长5%选取灵敏度分析参数样本，不考虑参数间相关性。按照式(8)分别计算混凝土施工中c、λ、β、Q04个热学参数对温度响应灵敏度，结果显示混凝土比热容和水泥水化热对温度变化起主导作用，导热系数和热交换系数影响相对较小。

3.3 混凝土热学参数反分析

考虑比热容和水化热的影响，采用二因子三水平的CCD试验设计找到13组参数，中心点重复5次。计算不同参数时混凝土施工温度响应值，以第1、3、6 d计算温度作为参数的响应值，设计参数和对应温度的数值区间如表1所示。

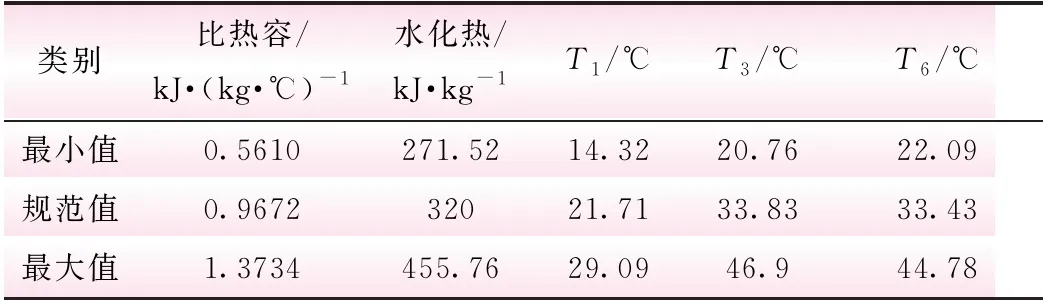
表1 混凝土热学参数值和温度值设计区间

依据式(2)及表1，对设计参数及响应值通过均一化映射到区间[-1，1]。将均一化的参数样本和第1、3、6 d的温度响应值利用公式(3)拟合，分别得到该结构浇筑第1、3、6 d改进的响应面模型。

该工程施工中混凝土浇筑的第1、3、6 d的实测温度分别为22.7、33.4、33.5 ℃。对实测温度利用式(2)处理，并根据式(6)计算得到混凝土热学参数反分析的目标函数如下

(9)

当热学参数取最优组合时，式(9)取最小值。据此，确定遗传算法适应度函数。根据要求，浇筑温度计算值与实测值的相对误差不应大于0.02，取ε=0.02，利用式(5)确定遗传算法的约束函数，并以此作为遗传算法程序寻优的终止条件。经迭代计算，得到最优参数组合c′=-0.28，Q′0=-0.08；将c′、Q′0的值代入式(2)，得到最优热学参数组合c=0.74 kJ/kg·℃，Q0=297.61 kJ/kg。

3.4 参数反分析结果验证

利用反分析得到的优化参数对该结构的有限元模型进行正分析，提取第1、3、6 d时各测点的温度，并将优化前后的温度响应对比如表2所示。

由表2可知，优化后结构的测点温度趋于实测温度，误差范围满足要求。此外，取S9和N9所对应的测点进行检验，测点温度计算值与实测值如图3所示。

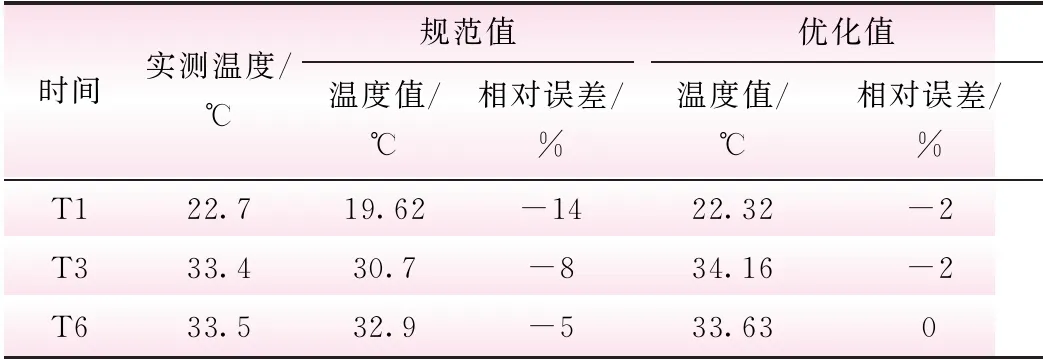
表2 优化前后温度响应值误差对比

图3 实测和计算温度值的对比

由图3可知，测点S9与测点N9的实测温度与对应的计算温度基本重合。说明融合人工智能遗传算法与改进响应面技术反分析混凝土热学参数精度较高，利用反分析优化得到的参数仿真分析可指导混凝土施工。

4 结 论

(1)提出了融合人工智能遗传算法与改进响应面技术的参数反分析算法，以实际工程实测数据为例，验证了该方法可减小参数区间和物理意义不同造成的模型误差，提高了参数反分析的效率和计算精度。

(2)混凝土热学参数反分析时将实测温度与计算温度的相对误差最小作为反分析目标，对混凝土热学参数进行反分析，根据最优参数仿真分析混凝土施工过程，测点温度计算结果与实测值基本一致。计算结果表明，利用融合人工智能遗传算法与改进响应面技术反分析得到的热学参数精度较高，利用反分析优化得到的参数仿真分析可为混凝土工程的合理施工及裂缝预防提出科学的建议。