大型社交网络的差分隐私保护算法

王婷婷，龙士工,2+，丁红发

(1.贵州大学 计算机科学与技术学院，贵州 贵阳 550025；2.贵州大学 公共大数据国家重点实验室，贵州 贵阳 550025；3.贵州财经大学 信息学院，贵州 贵阳 550025)

0 引 言

目前关于社交网络的差分隐私保护方法较多[1-4]，这些隐私保护方法虽然都能够抵抗背景知识攻击实现社交网络数据的隐私保护，但都只适用于小型社交网络，数据量不大。随着用户量增大、用户属性增多，这些方法都需要添加大量噪声，导致数据可用性变差；且当有n个社交用户时，需要发布n×n的大型矩阵，导致在计算和存储空间上的高成本。本文针对大型社交网络差分隐私保护中数据可用性过低的问题，提出了一种基于随机投影及差分隐私的大型社交网络隐私保护算法，该算法利用随机投影将高维社交网络数据映射到低维空间，再添加差分隐私噪声保护用户隐私。算法通过降低原始数据维度减少噪声添加，提高了数据可用性并保证了发布数据在基于欧式距离挖掘中数据可用性。

1 相关工作

差分隐私在社会网络隐私保护的研究主要集中于设计恰当的算法使其满足差分隐私和减少差分隐私噪声量两方面。Li等[1]针对用户的个人隐私偏好，提出了基于个性化差分隐私保护方法。Yan等[2]提出一种基于差分隐私和关联挖掘的社交网络隐私保护算法。Wang等[3]根据组间k-不可区分性将相同边权重的桶合并，减少了噪声添加。Karwa等[4]利用随机响应机制生成合成网络，利用似然估计推断丢失数据并将随机图模型拟合到生成的合成网络。Can等[5]提出了出度和分区的隐私保护方法，能有效降低算法敏感度，减少噪声量。Wang等[6]针对社交网络中实时数据发布问题提出动态分组机制和自适应预算分配机制，具有较强的隐私保障。Gao等[7]利用层次随机图描述原始社交网并通过马尔可夫链构造最佳匹配树，对节点加噪声后转化为下角矩阵。Liu等[8]将社交网络图进行划分，对划分后的图根据不同扰动策略和查询函数添加不同拉普拉斯噪声。但将这些方法运用到社交网络分析的主要特点是对计算和存储空间要求高，且当用户量大时需添加大量噪声，影响数据可用性。

鉴于现代社交网络用户数量庞大且属性值多，Wang等[9]提出了LNPP算法，通过计算邻接矩阵前k个特征值及其对应的特征向量，添加拉普拉斯噪声得到待发布数据，有效降低了发布矩阵维数并能够有效保留社交网络的光谱特征。Lan等[10]通过重构分割后的社交网络子图并用向量集来表示，构建满足Johnson-Lindenstrauss定理的映射函数，利用随机投影技术对高维向量集进行降维得到待发布向量集。综上所述，如何能够有效设计对大型社交网络隐私保护算法还相对较少，对高维复杂的社交网络数据进行降维并实现隐私保护，同时保持数据的高可用性，仍然具有挑战性。

针对上述问题，本文提出能保持数据高可用性的随机投影差分隐私保护算法。该算法首先利用随机投影对社交网络图的邻接矩阵进行降维，然后对降维后的矩阵进行差分隐私保护。通过理论和实验验证该算法满足(ε,δ)-差分隐私保护；对比结果表明，该算法比已有算法更加适用大规模社交网络数据发布的隐私保护，计算复杂度更低，数据效用更高。

2 相关知识

本章主要介绍关于社交网络图、随机投影和差分隐私基本概念及相关知识。

2.1 社交网络图

社交网络图表示用户个体以及用户个体之间的关系，设G=(V,{E})是一个表示社交网络连通性的二元图,V在图中的数据元素称为顶点V={v1,v2,…,vn},代表社交网络图中用户节点集合,{E}是用户节点之间边的集合，社交网络中用户节点数目为n=|V|。图1是简单的社交网络图。

图1 社交网络图G

2.2 随机投影

数据降维在数据挖掘和分析中有重要作用，随机投影相比于传统维数规约方法具有无需考虑原始数据本身固有的结构、计算负载低、运行效率高等特点，目前被广泛用于解决“维数爆炸”问题。随机投影技术属于低失真嵌入，利用矩阵相乘将原始高维空间投影到一个低维子空间，其重要理论依据就是Johnson-Lindenstrauss定理[11](简称J-L定理)。

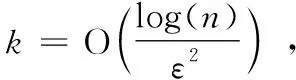
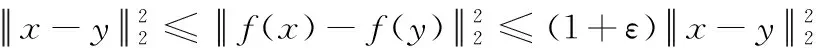
(1)

该定理说明在高维空间中的样本点可以在保持原始空间两个元素之间的欧式距离近似相等的情况下嵌入到低维空间中，通过减少数据维度来改变数据的原始形式，但仍能保持其统计特征。高斯随机矩阵[12]即矩阵中的元素服从高斯分布N(0,σ2)，是最早证明满足J-L定理的随机投影矩阵。

2.3 差分隐私

差分隐私保护模型忽略攻击者的背景知识以及不作任何限制性假设对手，可保障邻近数据集的查询输出具有概率不可区分性[13]。

定义1 (ε,δ)-差分隐私[14,15]：对于任意的两个数据集D1和D2，它们之间相差最多为一条记录，若一个随机函数A满足(ε,δ)-差分隐私保护，则对于所有的S⊆Range(K)有

Pr[A(D1)∈S]≤eεPr[A(D2)∈S]+δ

(2)

δ是差分隐私中精确性参数，当δ=0时，则称随机函数A满足ε-差分隐私保护。其中，Pr[E]表示事件E披露风险，ε是预算参数，代表了差分隐私保护水平，其值越小，隐私保护级别越高。

目前有3种噪声添加机制，分别是拉普拉斯机制(Laplace mechanism)、指数机制(exponential mechanism)和高斯机制(Gaussian mechanism)。其中，高斯机制在原始数据集中加入满足服从高斯分布的噪声来扰动原始数据以实现差分隐私保护[14]。拉普拉斯机制和高斯机制适用于数值型，而指数机制适用于非数值型。

定义2 高斯机制[15]:对于给定数据集合D，有查询函数f:D→R，如果有c2>2ln(1.25/δ),σ≥cΔ2f/ε并且N(0,σ2)独立同分布，则算法A满足

A(D)=f(D)+N(0,σ2)

(3)

Δ2f是查询函数的敏感度，与拉普拉斯机制中敏感度定义不同的是缩放到l2-敏感度而不再是缩放到l1-敏感度，其定义如下。

定义3 敏感度[15]:数据集D1和D2至多相差一条数据集，假设Δ2f是随机查询函数f的敏感度，则

(4)

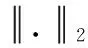
3 基于随机投影及差分隐私的社交网络隐私保护方法

本节针对有n个用户的社交网络数据，给出随机投影矩阵的敏感度定义和基于随机投影的差分隐私保护方法RP-DP(random projection and differential privacy)，并证明该算法能满足差分隐私需求，且数据保持较高可用性。

3.1 RP-DP算法

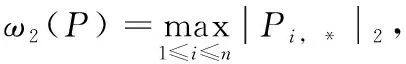
算法1：RP-DP算法

输入：社交网络图G，随机投影数量m，隐私保护水平ε，差分隐私参数δ

(1)建立社交网络图的邻接矩阵A←G，A∈Rn×n

(3)计算矩阵P的敏感度ω2(P)

(4)计算投影后的矩阵AP=A×P

(6)生成噪声矩阵Δ←Δi,j～N(0,σ2)

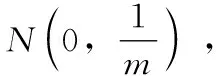
3.2 算法的差分隐私保证

本小节构造随机投影差分隐私定理，证明RP-DP算法满足(ε,δ)-差分隐私定义。

Pr[X+Δ∈D]≤eεPr[Y+Δ∈D]+δ

(5)

对式(5)的证明如下：

将集合D拆分成D1，D2两部分

D1=d∈D:X-Y,d-X≤ωR
D2=d∈D:X-Y,d-X>ωR

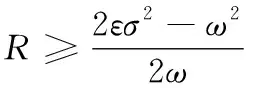
exp(ε)Pr[Y+Δ∈D1]

(6)

(7)

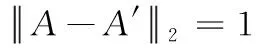
由定理2可知，在投影后的社交网络数据中添加服从高斯分布的噪声矩阵时，噪声矩阵的方差取决于投影矩阵的敏感度大小和隐私保护水平ε，敏感度越大，隐私预算参数越小方差越大。

3.3 数据可用性保证

本小节分析原始数据集经过RP-DP算法保护后，任意两用户间的欧几里得距离的平方在期望值相对不变，即保证原始社交网络数据在基于欧式距离分析挖掘中的数据可用性。

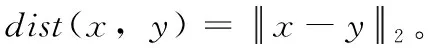
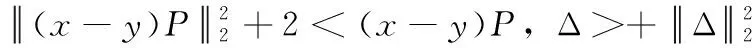
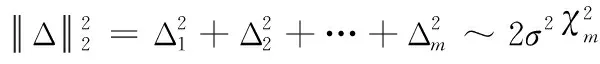
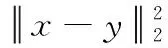
(8)

因此，如果对于指定投影维数m与隐私保护水平ε(定理2中σ值取等),那么任意两用户之间扰动后距离平方比原始距离平方的期望值多一个定值2mσ2。虽然用户之间的欧式距离会有一定偏移，但是相对距离基本保持不变，这意味在原始空间上接近的用户在隐私保护后的空间仍能保持接近。因此在数据挖掘过程中，对于基于欧式距离的算法分析时，数据仍保持可用性。

4 实验与对比

本节通过对斯坦福大学公开数据集SNAP Social networks中Bitcoin OTC子集(含5881个节点35 592条边)进行随机投影差分隐私保护和谱聚类实验，来验证RP-DP算法的有效性和数据可用性保持效果。

实验首先对原始数据集通过随机投影降至同一低维度并加入不同隐私保护水平的噪声矩阵，比较用户间欧氏距离的变化；其次，对原始数据集、差分隐私保护数据集和随机投影差分隐私数据集进行谱聚类实验，在不同隐私保护水平下，对比差分隐私算法和RP-DP算法的谱聚类效用NMI值变化；最后，利用RP-DP算法将原始社交网络数据集降至不同维度并添加不同隐私保护水平噪声，再对比数据聚类效用NMI值变化。

4.1 实验结果与分析

实验1：RP-DP算法在不同隐私预算下对社交网络用户间欧式距离的影响

为了验证RP-DP算法在不同隐私保护水平下，对社交网络用户间欧式距离的影响，实验1从Bitcoin OTC数据集中随机采样选取100个用户，并计算用户间原始欧式距离、经RP-DP算法在不同隐私保护水平下扰动后的欧式距离。该实验中，将Bitcoin OTC数据集降维至500维(m=500，即RP-DP算法不添加差分隐私噪声)及差分隐私保护水平分别设为ε=0.9,ε=0.7,ε=0.5,ε=0.3。为了实验结果的准确性，在每个隐私预算下进行100次实验后求平均值。实验结果如图2所示。

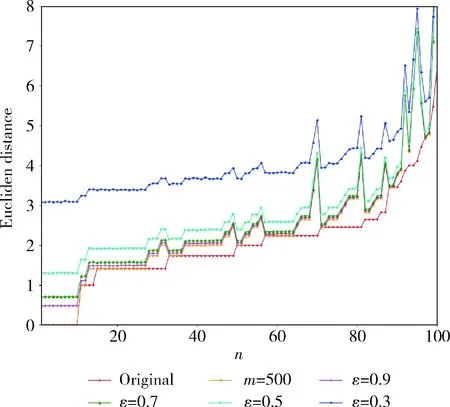
图2 用户间欧式距离变化对比

在图2中，m是投影数量，即将原始n×n维矩阵降至n×m维矩阵，ε是差分隐私预算参数，其值越小隐私保护水平越高。由图2可知，只对Bitcoin OTC数据集降至500维时，数据间距离变化不大，这符合J-L定理，高维空间中的数据在欧式距离近似相等的情况下可以嵌入到低维空间中；在隐私保护水平为ε=0.9，ε=0.7时，经RP-DP算法保护后的距离与原始距离偏离较小，随着隐私保护水平的增加，数据间的距离和原始距离偏差变大。但即使在高水平隐私保护水平下(ε=0.3)，数据间的相对距离也能保持不变，原始空间用户在转换后的空间上仍能保持偏序关系。

对实验1中用户间原始距离和不同隐私预算下的用户距离分别计算其均值、方差及相关系数各统计量的值，结果见表1。

由表1可知，对投影后的矩阵加入不同隐私保护程度噪声后，随着隐私保护水平的增高，加入的噪声量越大，用户间距离均值不断增大，方差逐渐减小，发布数据与原始数据的相关性递减。其中，均值变化表明RP-DP算法添加较少噪声时，对原始数据的影响较小，添加的噪声量越多，对原始数据的影响也越大；方差变化表明RP-DP算法随噪声的不断添加，对原始数据的隐私保护效果不断增强；相关系数变化表明，经过RP-DP算法保护后的发布数据能保持与原始数据较高的相关性，噪声对数据间的相关性影响不大，特别是添加少量噪声时(ε=0.9,ε=0.7)，能够保持与原始数据较高的相关性，仅当添加大量噪声(ε=0.3)时才会显著影响发布数据和原始数据间的相关性。

表1 用户距离各统计量对比

实验2：差分隐私算法与RP-DP算法对比实验

实验2对Bitcoin OTC数据集分别通过差分隐私算法[15]和RP-DP算法(m=500)保护后的发布数据集进行谱聚类(聚8类)对比，实验以Bitcoin OTC数据集不做变化直接聚类的结果作为标准划分，与两种发布数据集的聚类结果对比，计算标准化互信息(normalized mutual information，NMI)来衡量发布数据集的数据可用程度。NMI∈[0,1]，NMI值越大，X和Y划分就越相似，X表示原始数据的谱聚类结果，Y表示经过隐私保护算法后生成待发布数据集的谱聚类结果。实验结果如图3所示。

图3 不同隐私保护算法发布数据集相对原始数据集谱聚类的NMI对比(m=500)

图3是经过不同隐私保护算法生成的发布数据集相对原始数据集谱聚类的NMI对比图。在图3中，DP表示对Bitcoin OTC数据集进行差分隐私保护后相对原始数据集的谱聚类NMI在不同隐私预算下的变化曲线；RP-DP(m=500)表示对Bitcoin OTC数据集利用RP-DP算法降至500维时，通过RP-DP算法保护后相对原始数据集的谱聚类NMI在不同隐私预算下的变化曲线。由图3知，对数据集不降维直接利用DP算法保护社交网络数据，谱聚类结果相对于原始数据的NMI值小于0.1，数据可用性较差；当投影数量m=500时，利用RP-DP算法保护社交网络数据，在隐私保护水平ε>0.45时，NMI值大于0.7，数据有较好的可用性。图3表明差分隐私直接对大规模社交网络数据进行隐私保护，会导致数据可用性很差；通过RP-DP算法对大规模社交网络数据降维并进行隐私保护，可以保持数据较好的可用性。

实验3：RP-DP算法将原始数据降至不同维度随差分隐私预算变化的对比实验

为了评估RP-DP算法中投影数量对数据可用性影响，实验3将Bitcoin OTC数据集通过RP-DP算法降至不同维度，并调整差分隐私预算大小进行对比，结果如图4所示。

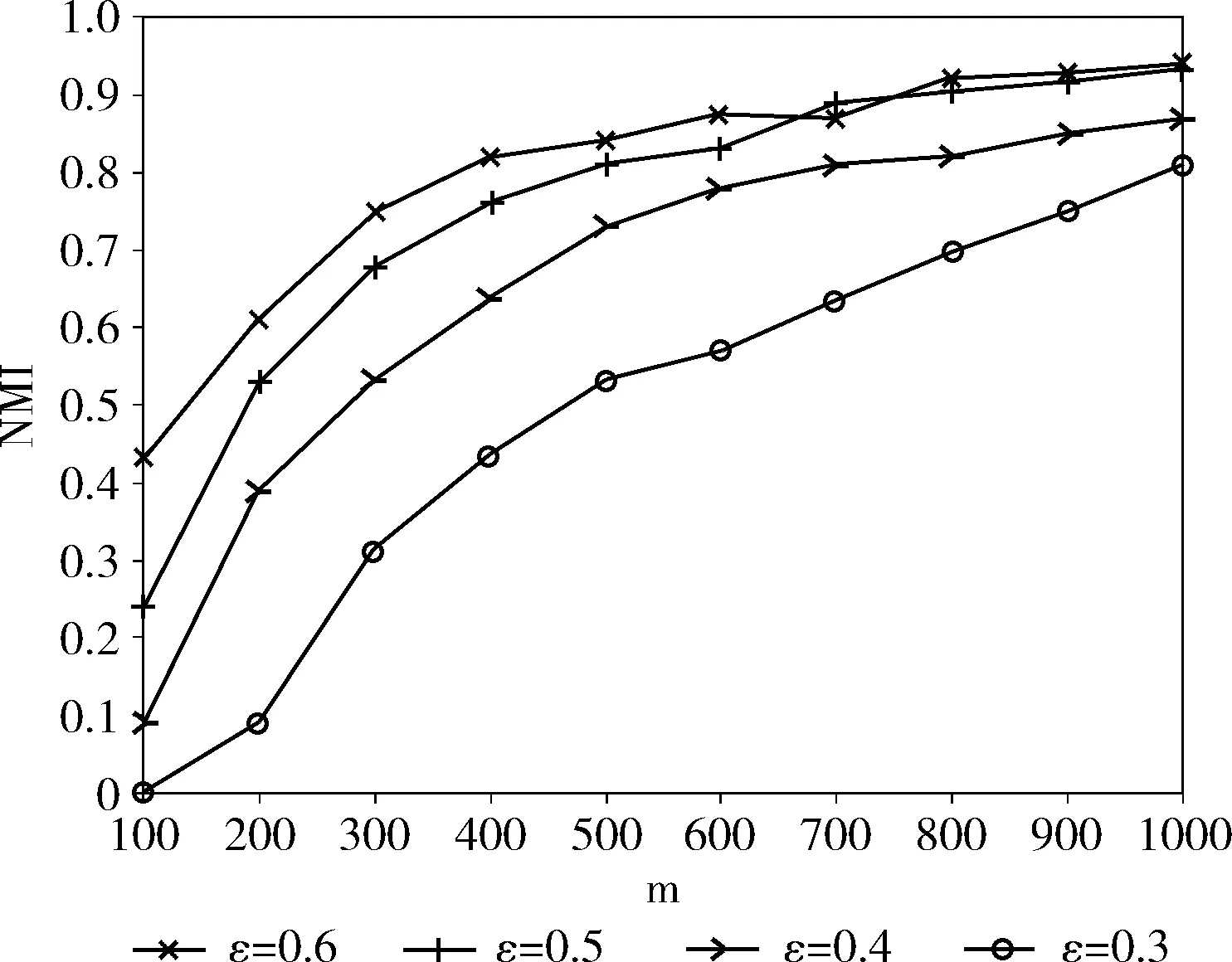
图4 RP-DP算法不同投影数量的发布数据集相对原始数据集谱聚类的NMI对比

图4是利用RP-DP算法对Bitcoin OTC数据集降至100-1000维度并添加不同差分隐私保护水平ε=0.6,ε=0.5,ε=0.4,ε=0.3下谱聚类NMI值变化曲线。图4表明，在相同隐私保护水平下，随着投影数量增加，数据可用性不断提高；投影到相同维度时，隐私保护程度越大，导致加入的噪声量越多，数据可用性变差。当投影数量小于200时，即使在低隐私保护水平ε=0.6，NMI值仍小于0.6，这是由于当投影数量m值变小时，一方面，降维过程中数据信息损耗增加；另一方面，投影矩阵的敏感度增加，噪声量的多少与敏感度成正比，影响了数据可用性。当投影数量大于500时，在高隐私保护水平ε=0.4的情况下，NMI值仍保持在0.72以上。

实验1表明，RP-DP算法通过随机投影将原始数据映射到低维子空间可以减少注入的噪声量，同时能够保持用户间欧氏距离的可计算性；实验2和实验3表明，差分隐私直接用于大型社交网络隐私保护时需要大量噪声，导致数据可用性过低，但利用RP-DP算法降维后能够有效减少噪声添加，提高了数据可用性。

4.2 对比分析

本小节将所提出RP-DP算法与相关文献性对比，见表2。

表2 社交网络差分隐私保护算法对比

表2中文献[3,7,9,10]和RP-DP算法都研究适用于社交网络的隐私保护算法，其中文献[3,7]是对社交网络采用不同的噪声机制实现差分隐私隐私保护，仅适用于小型社交网络数据发布；文献[9,10]和RP-DP算法适用于大规模社交网络数据发布，其中文献[9]中通过计算原始矩阵的前k个特征值与特征向量并添加拉普拉斯噪声生成待发布数据，降低了数据可用性且需要对原始矩阵进行计算，文献[10]中先将社交网划分为不同子图，再通过J-L定理降低向量维度，这样较大程度改变了社交网络图的原始结构，且隐私保护效果较差，而RP-DP算法利用随机投影降维并添加高斯噪声实现(ε,δ)-差分隐私保护。文献[17]利用主成分分析差分隐私通过添加拉普拉斯噪声达到隐私保护目的，该方法通过主成分分析对社交网络数据降维，需计算数据矩阵的协方差、特征值和特征向量，计算复杂度较高；RP-DP算法不需要存储原始数据或计算大型n×n矩阵，能够有效简化计算，并且只需要加入少量的噪声，提高了数据可用性。

5 结束语

本文针对面向数据挖掘的社交网络隐私保护数据发布和共享问题，提出了一种基于随机投影及差分隐私的大型社交网络数据发布算法。算法能够保证发布数据在基于欧式距离分析挖掘中的数据可用性；并有效降低待发布社交网络数据矩阵的维度，解决了发布n×n大型矩阵的困难，且差分隐私保护只需加入少量噪声，大大提高了数据可用性。此外，该算法比已有算法更加适用大规模社交网络数据，简化了计算复杂性。下一步的研究目标是当原始数据降至非常低维度时，如何提高数据可用性。