基于小波优化EEMD的二氧化硫检测

王志芳，王书涛, 王贵川, 车先阁

(燕山大学 电气工程学院，河北 秦皇岛 066004)

1 引 言

随着我国工业的发展，环境污染也越来越严重。环境污染可分为大气污染、水污染和土壤污染等[1]。近年来大气污染最为严重，SO2作为大气主要污染物之一，其含量的增加会引起人们呼吸道和心血管疾病[2,3]，且容易与水蒸气结合形成酸雨，导致土壤酸化严重危害农作物的生长[4]。我国现行环境空气质量标准[5]规定:空气中SO2的体积浓度年平均应低于21×10-9，日平均应低于52.5×10-9，时平均应低于1 775×10-9。大气中体积浓度远小于1%的低浓度气体称为痕量气体[6]，因此SO2的检测属于痕量气体检测，对检测技术要求较高。

SO2气体的检测方法有很多种[7]，如电导法、化学发光法和光谱学法等。光谱学检测方法中的紫外荧光法因其检测精度高、测量范围大、不需化学药剂等优点被广泛应用。紫外荧光法检测SO2浓度的主要原理是当SO2气体被激发光照射时，SO2吸收激发光特定波长值的能量，使SO2分子从基态进入激发态，当从激发态返回基态时会将多余的能量释放出来形成荧光，通过产生的荧光强度与SO2浓度的线性关系对SO2进行定量分析。由于待测的SO2气体浓度较低，产生的荧光光子数很少，容易被噪声淹没，因此荧光信号的去噪成为研究SO2检测的主要问题之一。王玉田等采用小波变换对SO2荧光检测信号进行去噪处理[8]；王书涛等采用经验模态分解算法对荧光法检测SO2浓度的信号进行去噪处理，将处理结果用于检测系统中，验证了经验模态分解算法用于SO2浓度检测的可行性[9]；王玉田等采用Boxcar滤波算法对淹没在本底噪声中的荧光信号进行有效提取和恢复，实现了对SO2荧光检测过程中的信号去噪[10]。

Huang N E等提出的经验模态分解(empirical mode decomposition, EMD)是一种自适应的处理方法[11]，可用于非线性信号。针对EMD分解时存在的模态混叠等问题，Wu Z H等提出了总体经验模态分解(ensemble empirical mode decomposition, EEMD)，通过添加高斯白噪声克服EMD的模态混叠问题[12]。EEMD方法可以将信号分解为若干个固有模态函数(intrinsic mode function, IMF)分量，通常认为噪声主要集中在高频IMF分量中，通过去除含噪IMF分量实现去噪[13,14]，但必然会去除部分有用信号，影响检测结果。本文采用小波优化EEMD方法，EEMD方法将原始信号分解为若干IMF分量后，用小波方法对IMF分量滤除噪声再进行信号重构，在更好地保存有用信号的前提下达到去噪的目的。

2 基本原理

2.1 EEMD方法原理

EEMD是为解决EMD分解时的模态混叠问题提出的[12]，模态混叠是由于极值点分布不均或极值点数目过少，对信号作包络时产生拟合误差造成的[15]。EEMD是在原始信号中加入高斯白噪声，利用高斯白噪声的频率平均分布特性，使信号在不同尺度成分上具有连续性，进而提供足够多的极值点用来平滑异常情况，多次EMD分解得到IMF分量后整体平均来克服模态混叠。而对于添加的高斯白噪声，因为其具有不相关随机序列零均值特性，整体平均后被剔除[16]。

EEMD分解步骤如下：

步骤1：给原始信号x(t)加入标准差为常数、均值为零的高斯白噪声ωi(t)，加入噪声次数为N，构成的初始信号xi(t)为：

xi(t)=x(t)+ωi(t)

(1)

式中:ωi(t)的大小由高斯白噪声的标准差和原始信号的标准差的比值k决定；i=1,2,…,N。

步骤2：对初始信号xi(t)进行EMD分解，获得M个IMF分量cj(t)和余项ri(t)，j=1,2,…,M。

重复步骤1和2共N次，即添加白噪声的次数为N，每次加入的高斯白噪声序列不同。则xi(t)可表示为：

(2)

式中cij(t)为第i次加入高斯白噪声后分解得到的第j个IMF分量。

步骤3：计算各个IMF分量cij(t)的平均值作为最终结果，即：

(3)

(4)

式中:cj(t)是信号x(t)进行EEMD分解后第j个IMF分量；r(t)是余项。因为高斯白噪声具有频谱均值为零的特性，故高斯白噪声在IMF求平均后被抵消。

EEMD的分解流程图如图1。

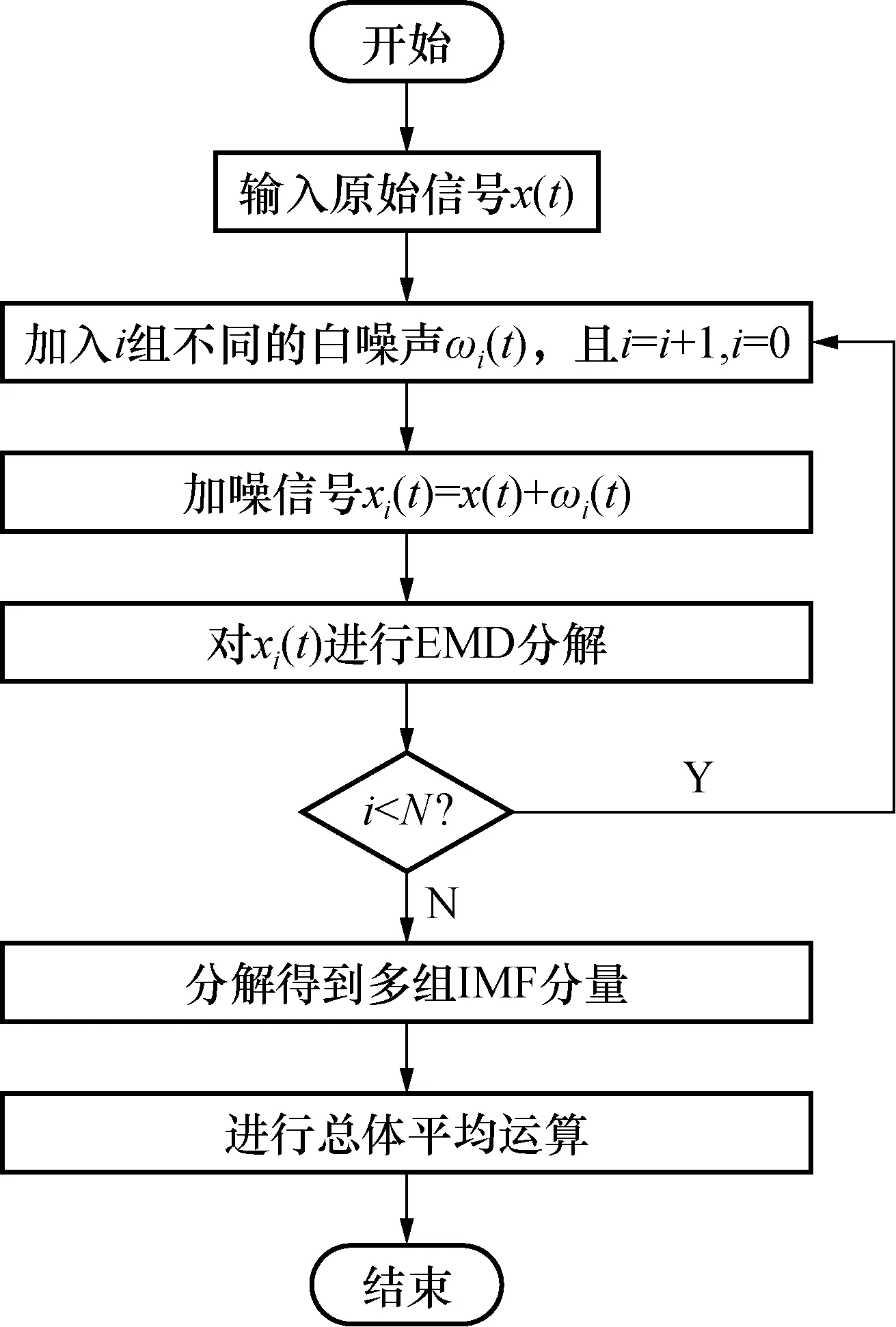
图1 EEMD流程图

2.2 小波去噪基础

小波分析是在傅里叶变换基础上发展的，属于信号时频分析方法。在信号分析和图像处理领域有较广泛的应用，例如信号滤波、信号去噪[17]等。小波去噪算法包括3种：小波阈值去噪、基于小波系数的相关性去噪、基于模极大值的去噪。其中小波阈值去噪因其简单易实现、计算量小、多分辨率等优点被广泛应用。小波阈值去噪算法中常见的小波基函数有：Haar、Daubechies、Mexican Hat、Morlet、Meyer等。Daubechies函数可简写为dbN，N为小波阶数，dbN小波函数需要的滤波器系数少、有较好的紧支性和正交性。

小波去噪步骤：

步骤1：信号分解。确定分解层数j，对信号进行j层分解。

步骤2：对分解得到的小波系数进行软阈值去噪。小波分解后分为高频成分和低频成分，对每层分解的高频成分进行阈值去噪。

步骤3：信号重构。对小波分解最后得到的第j层低频成分信号和经过去噪的高频成分信号进行重构，得到去噪信号。

2.3 小波优化EEMD的去噪方法

EEMD去噪方法是通过分解后去除含有噪声的高频IMF分量来达到去噪效果，但同时将高频IMF分量中的有效信号也去除掉了。利用小波优化EEMD的去噪方法，对于分解后得到的IMF分量，用小波阈值对各IMF分量进行去噪处理，再将处理后的IMF分量进行重构，有效去除噪声信号的同时保留了有效信号。

基于小波改进EEMD的去噪方法对SO2荧光信号进行去噪处理的步骤：

步骤1：EEMD分解。首先对得到的SO2荧光信号x(t)进行EEMD分解，得到一组IMF分量；

步骤2：IMF分量的去噪。对各个IMF分量进行小波阈值去噪，得到去噪后的IMF分量；

步骤3：信号重构。将小波阈值去噪后的各IMF分量进行重构，得到去噪后的SO2荧光信号x′(t)。

基于小波优化EEMD的算法流程如图2所示。

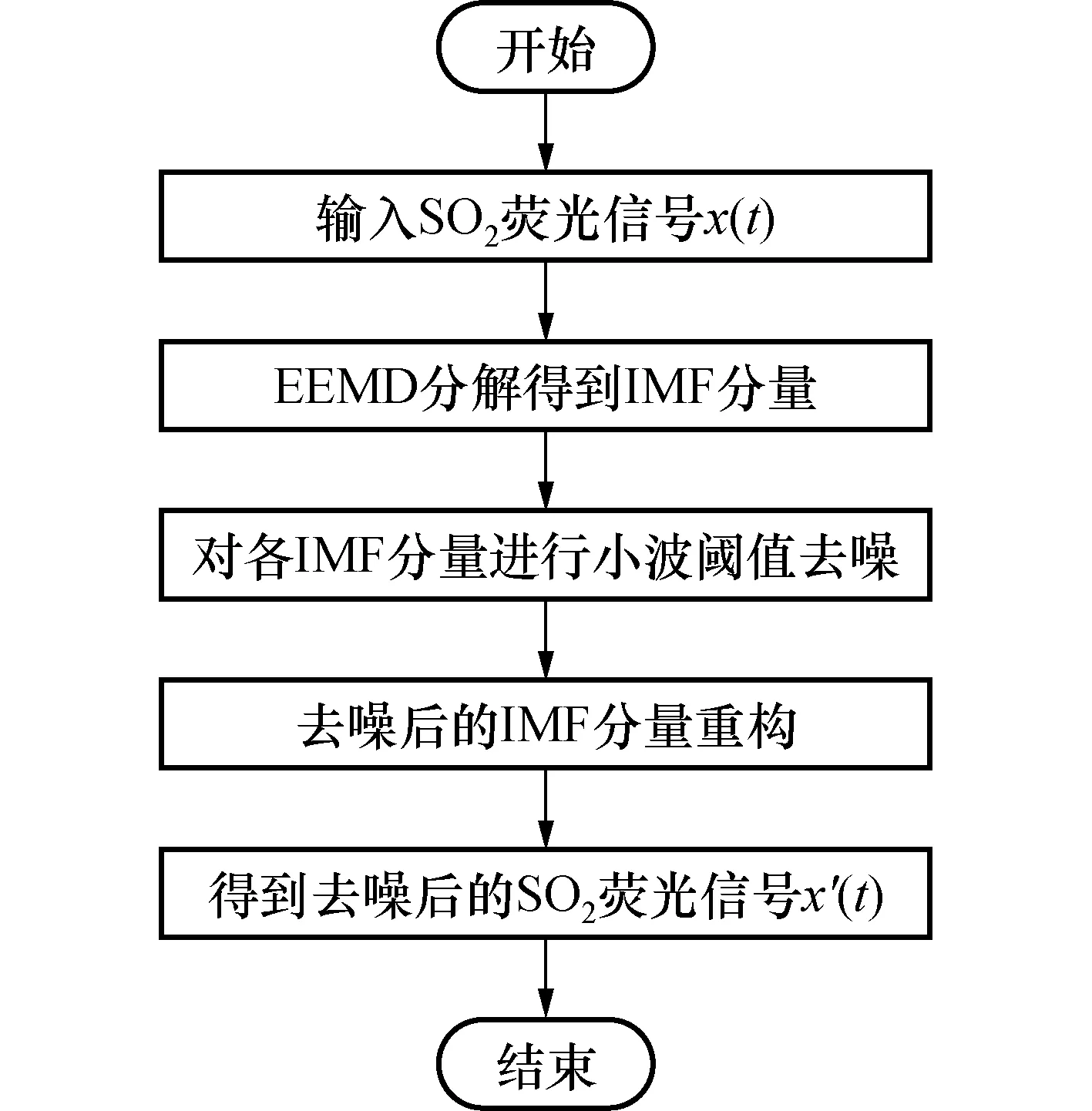
图2 基于小波优化的EEMD去噪算法流程图

3 实验与分析

3.1 SO2检测系统

图3为SO2紫外荧光检测系统，检测系统主要由光源、光路、气室和信号接收和处理部分组成。光电倍增管PMT1接收荧光信号，光电倍增管PMT2接收到的透射光信号作为参考信号，抑制光源波动对检测造成的影响；其中光源选用北京卓立公司生产的LHD30型号的氘灯，PMT采用Hamamatsu公司研制的R212型PMT。

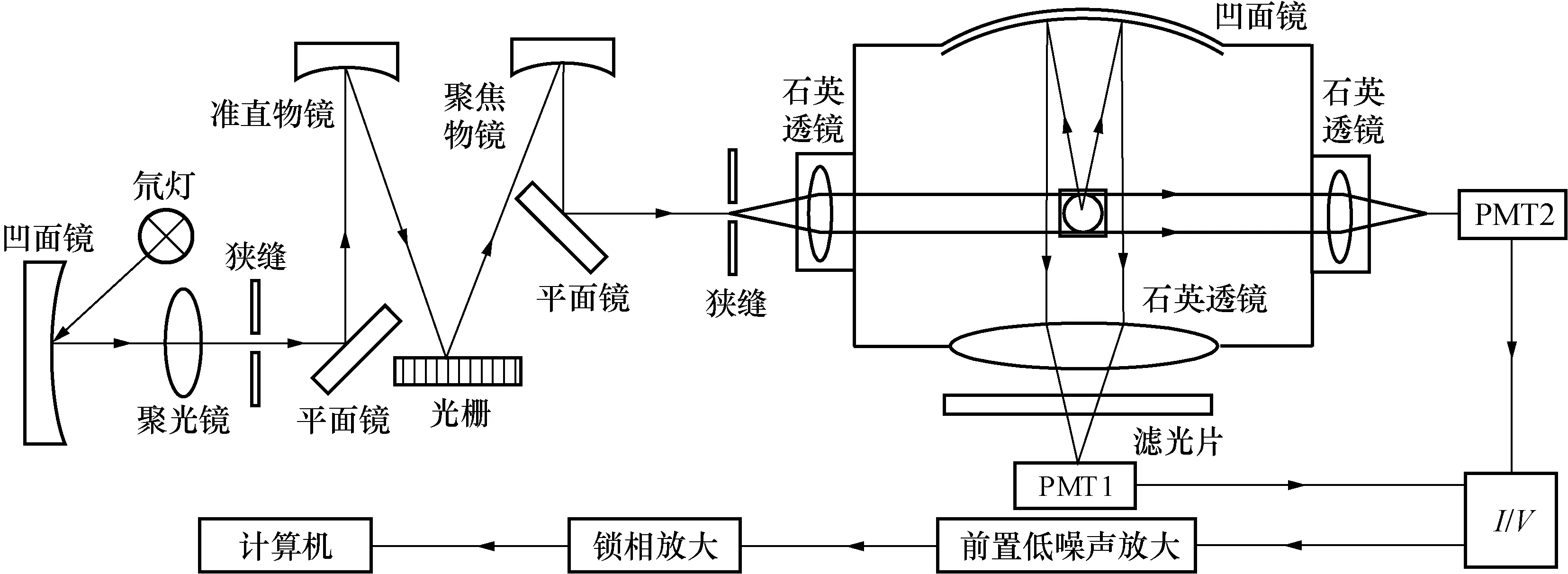
图3 SO2紫外荧光检测系统

在室温25 ℃，101.325 kPa(1个标准大气压)下，用EN4000配气仪配制体积浓度为50×10-6,70×10-6,100×10-6,200×10-6,300×10-6,400×10-6,500×10-6,600×10-6的SO2标准气体，分别通入系统中。为保证实验中SO2气体浓度的准确性，采用美国TE公司的Model 111型零气发生器，在检测某一种浓度的SO2气体前首先通过零气，之后转换气路通入SO2气体，检测完成后再通入零气，然后再次通入待测的SO2气体，如此循环。每种浓度的SO2气体测量3次，实验数据如表1所示。

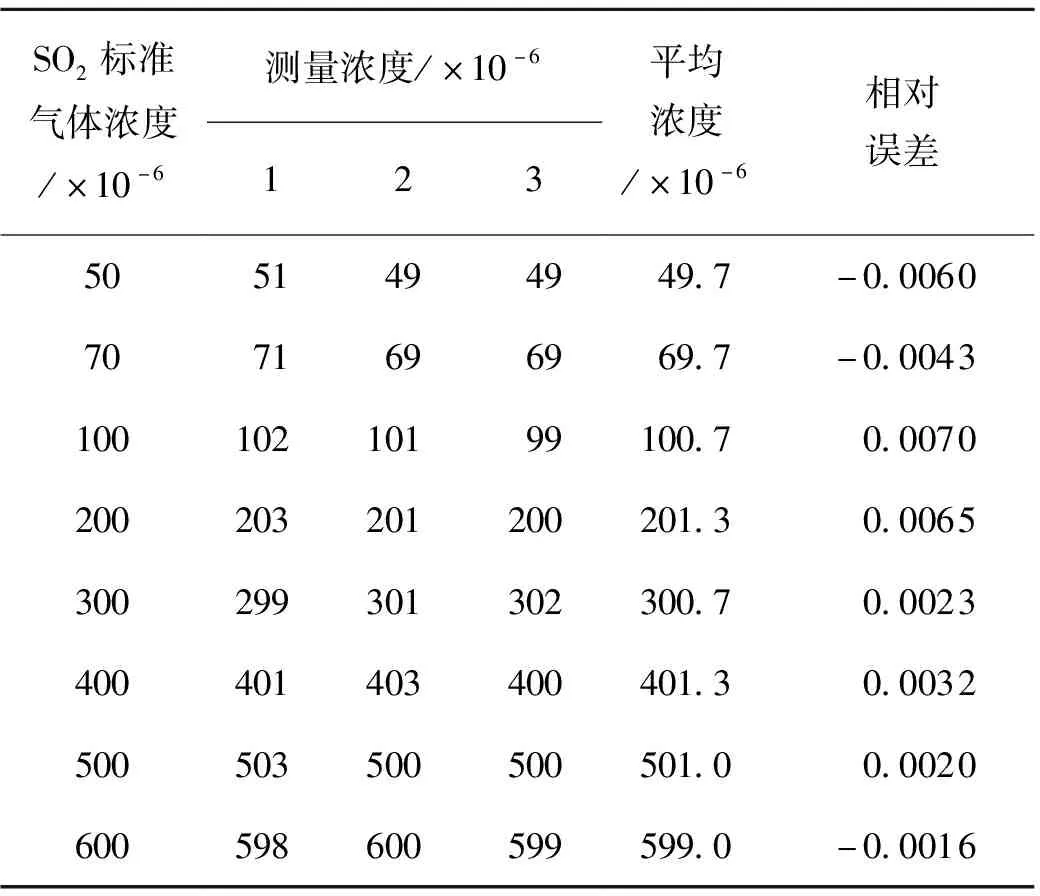
表1 SO2气体标准浓度和检测浓度

由表1可以看出，实测SO2气体浓度和标准浓度最大相对误差不超过0.010 0，平均相对误差为 0.001 1。绘制SO2浓度与测得电压值的关系曲线，如图4所示。从图4可以看出，SO2浓度与电压成线性关系，线性相关系数为0.978 0，线性方程为y=0.009 3x+0.030 7。

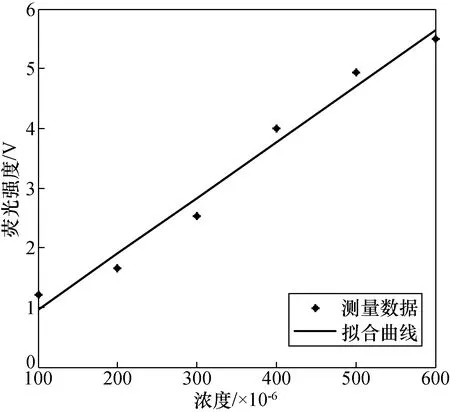
图4 SO2浓度与荧光强度关系

SO2体积浓度为50×10-6时，0.4 s内光电倍增管接收到的SO2荧光强度的信号如图5所示。从图5可以看出，SO2荧光信号中含有大量噪声，将有用信号淹没。

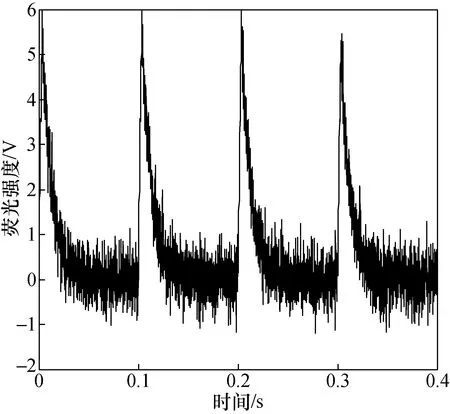
图5 SO2荧光信号

3.2 信号去噪

图5中SO2荧光信号中含有大量的噪声信号，影响检测结果的分析，有必要对信号进行去噪处理。为了分析去噪方法的效果，选取1个周期内(0～0.1 s)的荧光信号进行去噪处理。

首先对SO2荧光信号进行EEMD分解，经过多次调试，确定EEMD中添加的白噪声次数为150，标准差为0.15。分解得到9个IMF分量(IMF1～IMF9)，如图6所示。采用db12小波对各IMF分量进行5层分解去噪，去噪效果如图7所示。

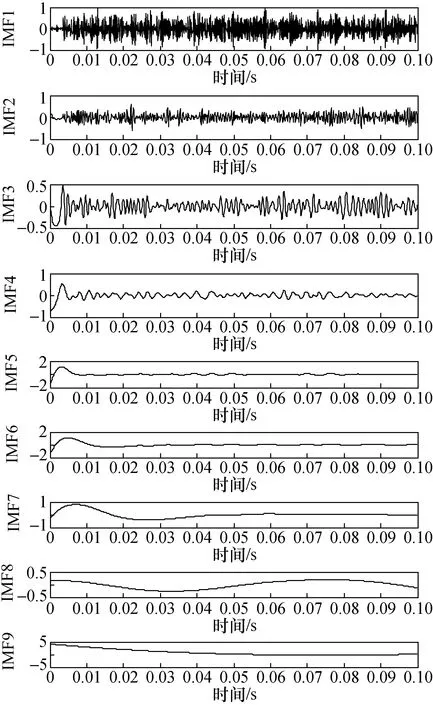
图6 EEMD分解过程

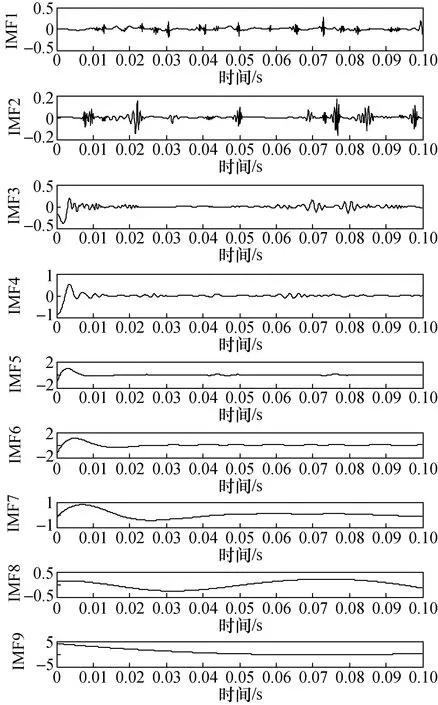
图7 小波去噪后的IMF分量

把小波去噪后的各IMF分量重构，得到小波优化的EEMD方法去噪后的SO2荧光光谱，如图8所示。

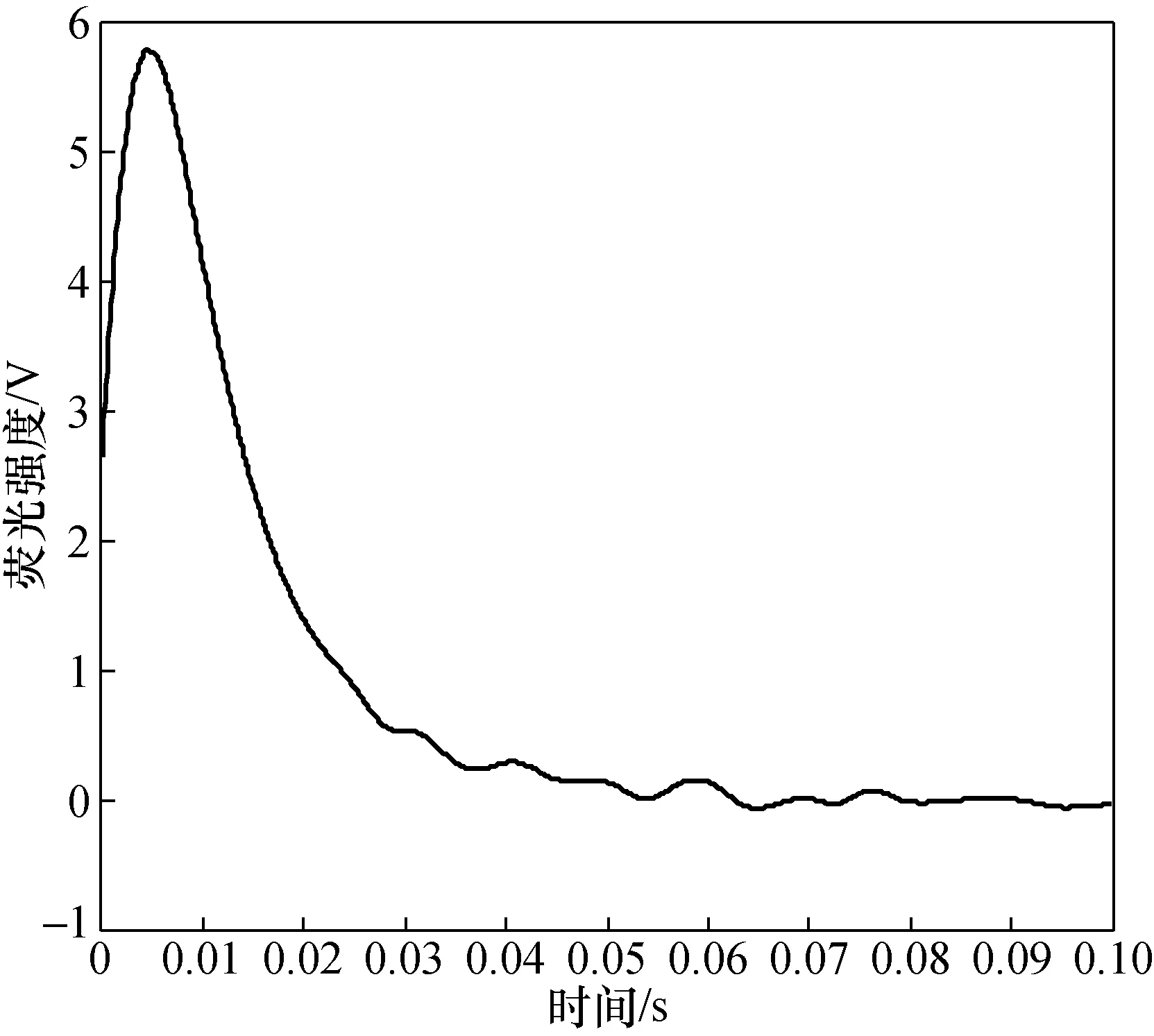
图8 基于小波优化的EEMD去噪SO2荧光光谱

3.3 去噪效果评价

为证明小波优化的EEMD对SO2荧光光谱的去噪有更好的效果，与EEMD和小波去噪方法进行比较。图9为EEMD去噪后的SO2荧光光谱，图10为采用db12小波进行5层分解去噪后的SO2荧光光谱。对比图8、图9和图10，可以看出，利用小波优化的EEMD对SO2荧光光谱去噪后的光谱曲线相对EEMD和小波去噪后的SO2荧光光谱曲线更加平滑。

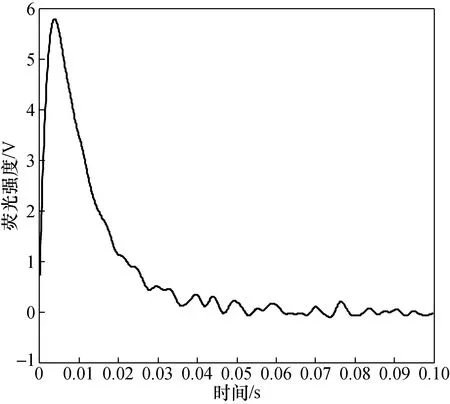
图9 EEMD去噪后的SO2荧光光谱

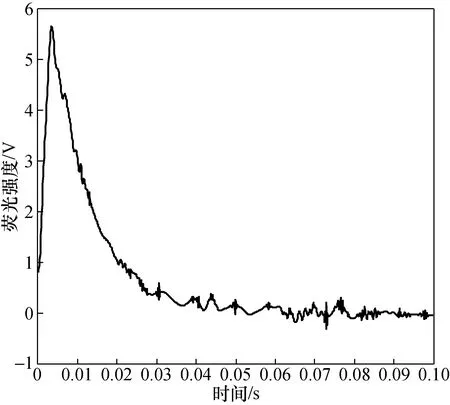
图10 小波去噪后的SO2荧光光谱

为了更直观的比较3种去噪方法的去噪效果，采用信噪比(signal noise ratio, SNR)、均方误差(mean square error, MSE)和归一化相关系数(normalized correlation coefficient, NCC)对3种去噪方法进行比较。SNR、MSE和NCC的计算式分别为：

(6)

(7)

(8)

式中：N表示采样数；yi表示时刻i去噪后的信号值；xi表示时刻i原信号值。

在3种去噪效果评价指标中，SNR体现算法的去噪能力，SNR值越大去噪效果越好；MSE表示去噪后的光谱与原始光谱的幅值对比，MSE值越小越好；NCC表示去噪后的光谱与原始光谱波形的相似度，数值范围为[-1,1]，-1表示去噪后波形与原波形反向，0表示正交，1表示两波形完全相同[18]。将去噪前后的信号值带入式(6)～式(8)中，得到基于小波优化的EEMD、EEMD和小波3种去噪方法的性能指标值如表2。

从表2中可以看出，3种去噪方法的SNR和MSE效果排序分别是小波优化的EEMD>EEMD>小波，NCC效果排序是小波优化的EEMD>小波>EEMD。综合3个去噪性能指标可以看出，基于小波优化的EEMD方法对SO2荧光光谱的去噪效果最佳。

将小波优化EEMD的去噪结果用于SO2荧光检测系统中，再次计算SO2浓度和荧光强度的线性关系，如图11所示。其中，SO2浓度与荧光强度的线性关系为0.993 6，线性方程为y=0.008 9x+0.215 3。

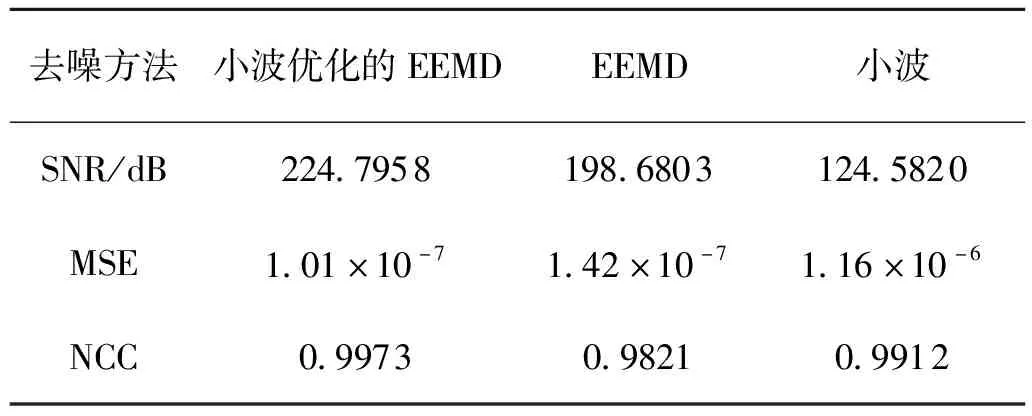
表2 3种去噪方法性能比较

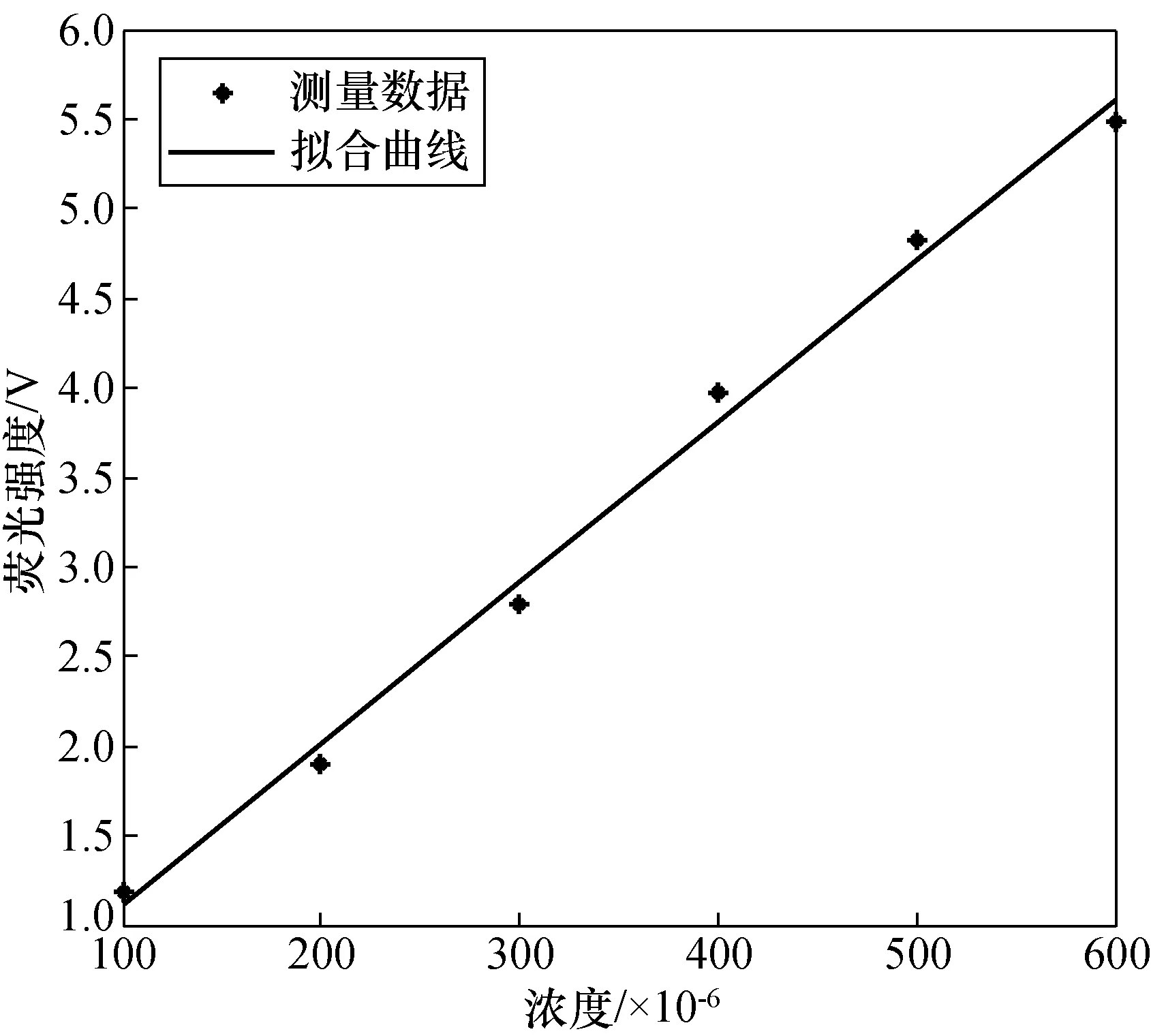
图11 去噪后的SO2浓度与荧光强度关系

5 结 论

基于紫外荧光光谱法检测SO2气体浓度，搭建SO2紫外荧光检测系统进行SO2浓度检测，分别进行50×10-6,70×10-6,100×10-6,200×10-6,300×10-6,400×10-6,500×10-6和600×10-6共8种浓度的SO2气体检测，检测结果的平均误差为0.001 1，SO2气体浓度与荧光强度的线性相关系数为0.978 0。对浓度为50×10-6的SO2的荧光光谱，采用小波算法优化EEMD进行去噪，EEMD分解得到一组IMF分量，利用小波对各IMF分量进行去噪后再进行重构，得到去噪后的SO2荧光光谱。将基于小波优化的EEMD去噪方法用于系统中，得到SO2浓度与荧光强度的线性相关系数为0.993 6。另外，分别用EEMD和小波去噪方法对SO2荧光光谱进行去噪，通过信噪比、均方误差和波形相似系数来比较3种去噪方法的去噪效果。实验得出小波优化的EEMD对SO2荧光光谱的去噪后的信噪比和均方误差分别为224.795 8 dB和1.01×10-7，波形相似系数为0.997 3；表明小波优化的EEMD去噪方法在较好地保留了有用信息的前提下，去噪效果更好。