变截面滑靴结构强度有限元设计

吕 超，杨风艳，杨明旺，刘广辉，谷学准

(海洋石油工程(青岛)有限公司，山东青岛 266520)

组块、导管架等大型海洋工程结构物，放置在滑靴上建造，建造完成后通过滑道完成滑移装船，滑靴在建造和装船过程中，承受着来自上部结构物的所有荷载。

建造过程中，由于上部组快、导管架等结构物的重力作用，因此，变截面滑靴强度校核时，只需要考虑垂直方向的重力载荷，且在整个建造过程中重力会随着上部结构物的总装逐渐变大；装船时，由于受到来自拉力千斤顶的水平方向拖拽作用，变截面滑靴不仅仅受到重力载荷作用，还受到水平载荷作用；除此以外，装船时还需要考虑上部结构物桩腿失效造成的变截面滑靴受到载荷变大的工况。根据不同的装船方式，滑靴主要分为连续滑靴、变截面滑靴和等截面滑靴等。本文以变截面滑靴为研究对象，使用ANSYS软件，剖析滑靴强度的有限元分析技术。

1 单元类型选择

ANSYS软件提供了多种壳单元，如SHELL41、SHELL43、SHELL51、SHELL63、SHELL141、SHELL181。其中，SHELL63单元是最常用的一种弹性薄壳单元。类似的单元包括：SOLID46、SOLID64、SOLID65、SOLID92、SOLID95、SOLID185等。

为使设计结果更加准确，根据变截面滑靴由薄板、薄壳组成的特点，对变截面滑靴的有限元模拟，应该采用壳单元还是实体单元，可以使用使用单根梁为例，通过对比计算，选择合适的单元类型。需要提前设置号的有限元模型参数主要包括，弹性模量，泊松比，梁的截面尺寸和长度，本文使用空心的矩形截面梁。约束情况可以使用最简单的简支梁或悬臂梁，载荷位置最好在简支梁的中间或者悬臂梁的终端，本文使用悬臂梁并将载荷施加在梁的自由端。

根据计算结果对比不同单元类型情况下，梁跨中截面正应力值可知，壳单元有限元解比理论值偏低；实体单元有限元解与理论值吻合较好，且高阶单元(SOLID186、SOLID187)有限元解明显优于低阶单元(SOLID185、SOLID285)。变截面滑靴有限模型(壳单元、实体)见图1、图。相应地，采用高阶单元进行有限元计算时所消耗的时间明显高于低阶单元。

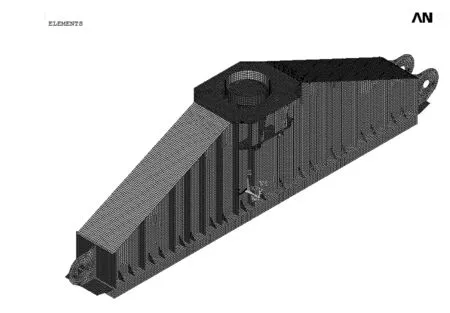
图1 变截面滑靴有限模型(壳单元)

图2 变截面滑靴有限模型(实体)

对于实体单元，当网格尺寸不同时，有限元所得的解会不相同，SOLID186-20单元的节点六面体受单元尺寸的影响更加明显。但当SOLID185单元尺寸进一步缩小时，有限元解变化不大，求解耗时却大幅增加。因此，本文使用Solid185对变截面滑靴进行有限元强度计算。

2 倒角

在采用相同模型、不同网格尺寸条件下，无倒角和有倒角的应力计算结果如表1，图3、图4。

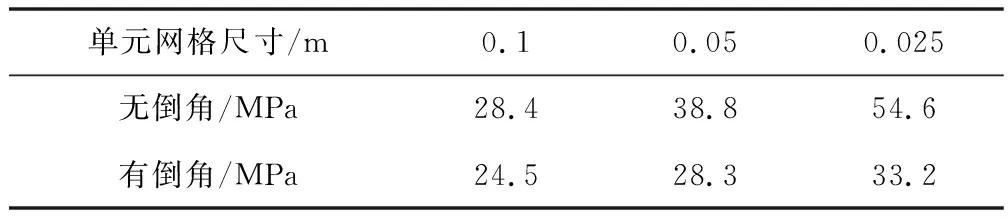
表1 无倒角和有倒角应力计算结果

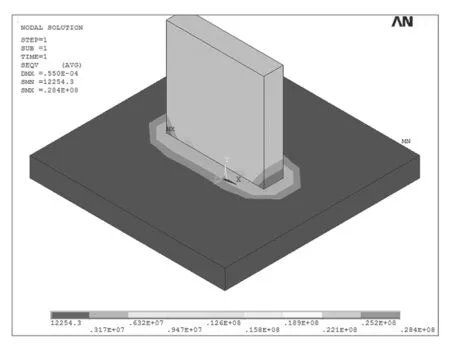
图3 无倒角模型计算结果

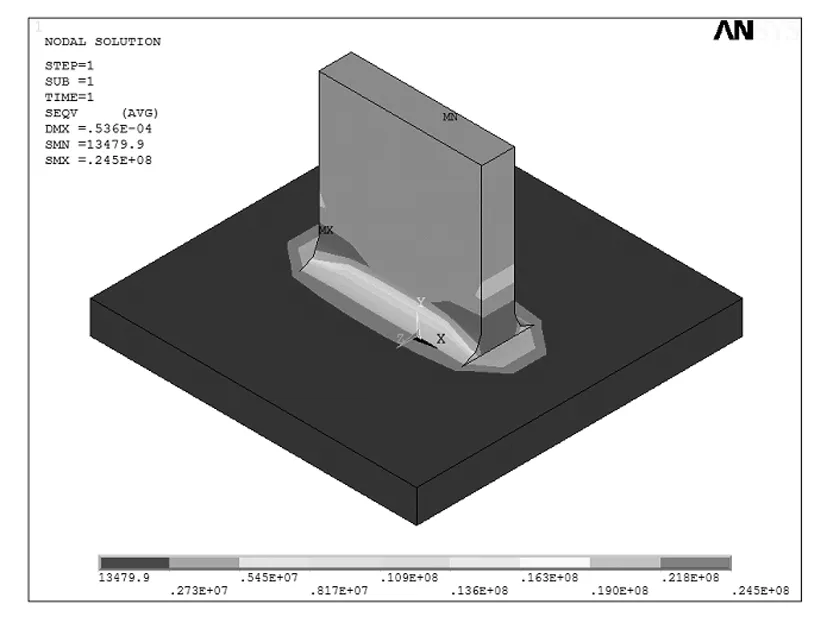
图4 0.6倍倒角模型计算结果

无倒角的应力结果随网格密度增大，在板直角相接处的应力集中也会逐步增大；对比相同网格尺寸下，无倒角与倒角后的应力值，倒角对应力集中有一定的调节作用，且随网格加密调节作用越明显。

3 桩腿高度

分别使用高度为1/4，1/2，3/4，1倍桩腿直径的桩腿高度进行计算，当支撑桩腿高度在上述四种高度之间变化时，整个滑靴的米塞斯应力计算结果差别非常小，桩腿高度对于变截面化学的强度设计的影响可以忽略。另外，从支撑导管应力分布图中可以看出，当导管高度较小时，顶部与底部应力值较大的区域交织在一起，这属于圣维南原理现象，此时的桩腿高度不合理。在这种桩腿高度条件下，不能消除边界效应问题。随着桩腿高度增加，这种影响会逐步减小直至消失。因此，选择有限元模型的桩腿高度为1/2直径较为合适。

4 变截面滑靴有限元模型

滑靴钢结构部分采用实体单元，滑靴底部和滑道直接接触的木材，考虑各项异性。载荷施加在顶部桩腿薄壳面上。对于有限元模型的约束位置，可以施加在滑靴底部垫木上，在垫木中线位置、地面位置和前后左右的侧面位置施加约束(见图5、图6)。

计算结果表明：对比XYZ约束及正交约束，两种约束方案关键位置处的最大米塞斯应力大小及位置均近似一致；不同约束方案米塞斯应力变化不大，表明约束对计算结果的影响不大，其原因在于滑靴结构及载荷均对称，且载荷方向竖直向下。

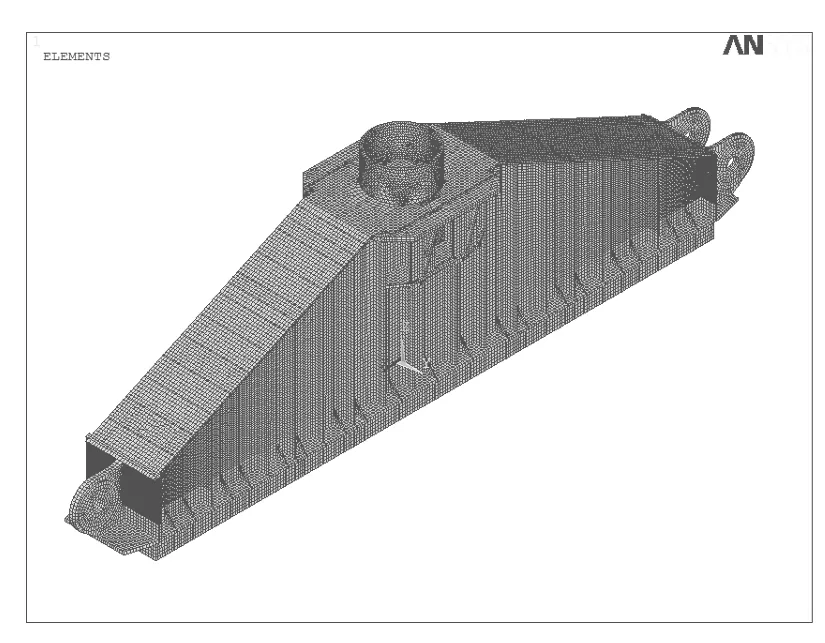
图5 变截面滑靴有限元模型

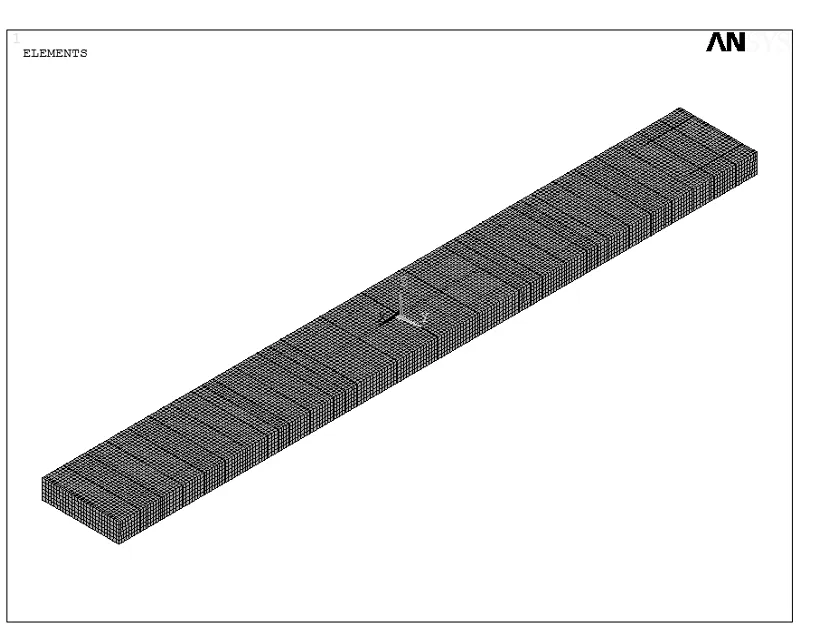
图6 变截面滑靴垫木材有限元模型

5 变截面滑靴装船过程平稳工况下有限元设计

根据有限元计算结果，采用弹性分析时，米塞斯应力最大值超过屈服强度；由于拖点应力超过屈服应力，故采用弹塑性分析，此时米塞斯应力最大值还是超过屈服强度，最大米塞斯应力发生位置在拖点处；如果不考虑拖点，滑靴最大米塞斯应力远小于屈服强度。根据弹性分析计算结果，底部钢板米塞斯应力最大值为也远小于屈服强度；下表面应力分布比上表面更加均匀。滑靴顶板与桩腿米塞斯应力最大值低于屈服极限。最大米塞斯应力在桩腿与顶板接触处；根据弹性分析结果，在桩腿位置处部分单元进入塑性阶段(见图7)。

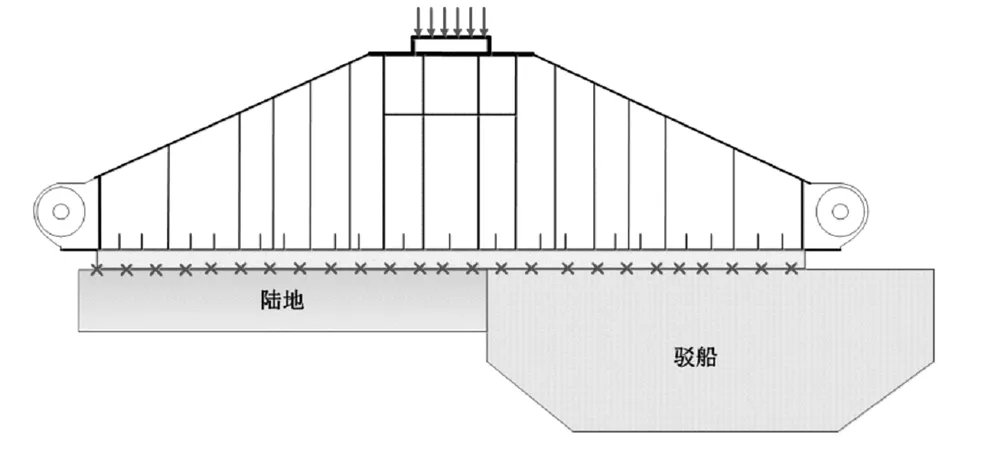
图7 平稳工况下受力分析模型

通过对比分析塑性计算结果，变截面滑靴顶部钢板与桩腿的接触位置，并未发生塑性变形，但是应力计算结果高出其它位置，所以，在实际工程中，此位置应当布置加强筋板，提高该位置的承载能力。另外，装船工况下，该位置的应力比建造工况下变大，主要原因在于，一个方向受到压力作用、另外一个方向受到拉力作用。

6 变截面滑靴装船过程不平稳工况下有限元设计

装船时，使用拉力千斤顶拖拉变截面滑靴前端的拖点，拖拽里的作用方向为水平方向，该水平方向的力主要克服水平变截面滑靴和滑道板之间的摩擦力，由于已经提前铺设特氟龙板在滑道板上，因此，滑靴下方木头和滑道板间的静摩擦系数取0.2。装船过程中，滑靴部分位于码头侧的滑道上面，部分转移到了船舶上的钢制滑道。若船体下沉，则会对滑靴底部的约束产生影响。滑靴上船部分小于二分之一，则陆地部分依然XYZ全约束，上船部分悬空，予以放松约束；滑靴上船部分大于二分之一，则滑靴转移至船上，由驳船承载。

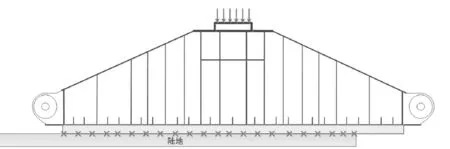
图8 滑靴装船过程受力分析模型

6.1 滑靴八分之七位于陆地有限元结果分析

采用弹性分析时，米塞斯应力最大值超过屈服强度；由于拖点应力超过屈服应力，故采用弹塑性分析，此时米塞斯应力最大值还是超过屈服强度，最大米塞斯应力发生位置在拖点处；垫木应力最大值发生位置在约束改变处；主要原因是部分悬空使得垫木承受较大应力，类似于剪切变形。根据塑性分析计算结果，底部钢板米塞斯应力最大值未超过屈服极限；下表面应力分布比上表面更加均匀。滑靴顶板与桩腿连接位置处，米塞斯应力最大值低于屈服极限。最大米塞斯应力在桩腿与顶板接触处；根据弹性分析结果，在桩腿位置处单元仍处于弹性，但该处应力高于其他位置应力较多。在桩腿与滑靴顶部钢板接触位置，计算结果和第5部分分布规律相同，主要原因在于，一个方向受到压力作用、另外一个方向受到拉力作用。根据弹塑性分析结果，米塞斯应力最大点首先出现在与水平方向夹角为45度的两个点，然后向中部扩散，在实际项目中应采取相应措施。

6.2 滑靴八分之六位于陆地有限元结果分析

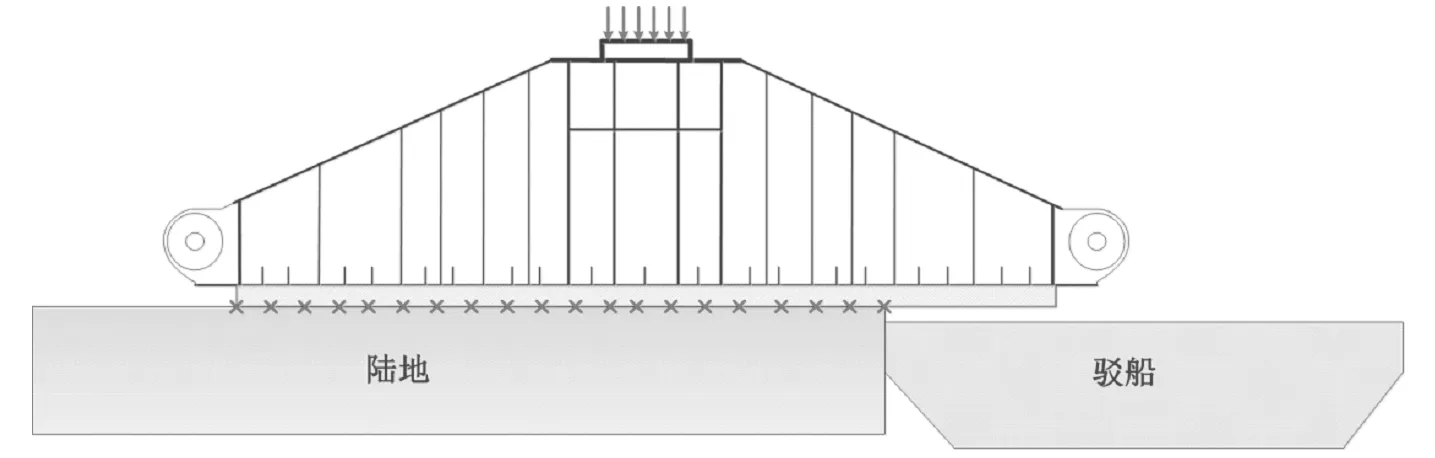
图9 滑靴八分之六位于陆地受力分析模型

采用弹性分析时，米塞斯应力最大值超过屈服强度；由于拖点应力超过屈服应力，故采用弹塑性分析，此时米塞斯应力最大值还是超过屈服强度，最大米塞斯应力发生位置在拖点处；滑靴垫木应力值最大值出现在极个别单元。底部钢板应力分布规律与约束位置关系密切；已上船部分钢板应力明显高于未上船部分。对于滑靴顶板与桩腿，应力大小及分布规律变化与其他阶段相比变化不大对于拖点，应力大小及分布规律变化与其他阶段相比变化不大；主要原因在于：拖点主要承受拉力作用，上部桩腿传递到拖点的压力对拖点影响较小(见图9)。

6.3 滑靴八分之四上船有限元结果分析

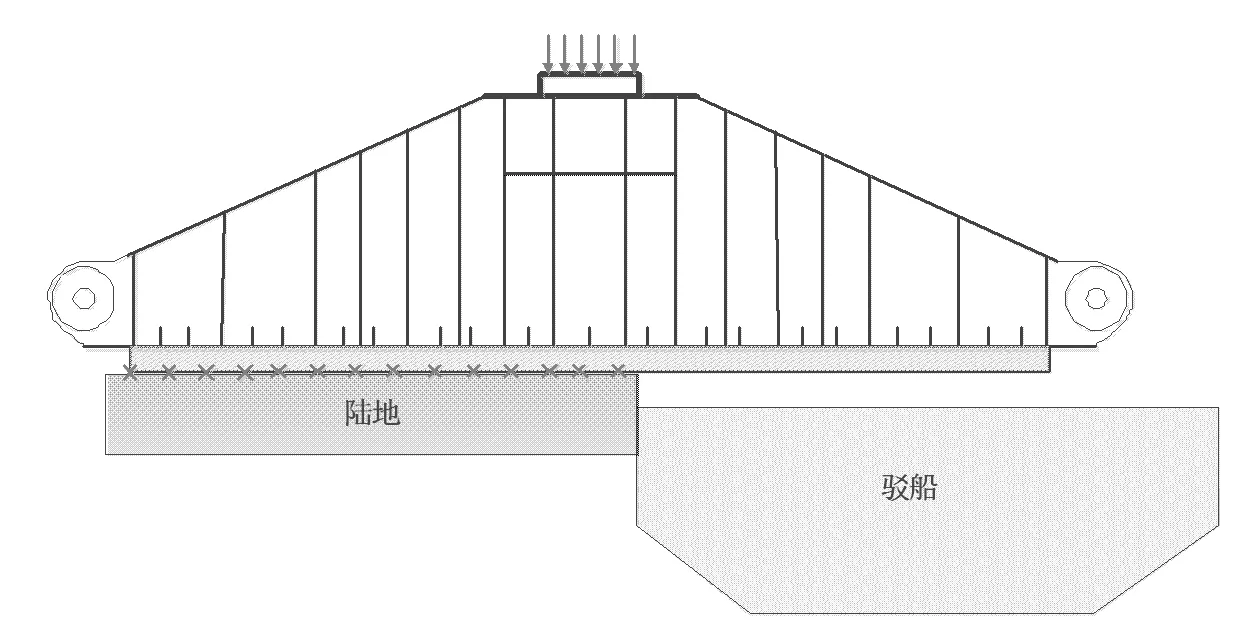
图10 滑靴八分之四上船受力分析模型

采用弹性分析时，米塞斯应力最大值远超过屈服强度；由于拖点应力超过屈服应力，故采用弹塑性分析，此时米塞斯应力最大值还是超过屈服强度，最大米塞斯应力发生位置在拖点处；在上船到一半的时候，若发生船体下沉，垫木应力高；建议应重点监控上船至一半的过程。在上船到一半的时候，若发生船体下沉，底部钢板应力高；建议应重点监控上船至一半的过程。在底部钢板上应力分布规律极不平均。对于滑靴顶板与桩腿，上船到变截面滑靴中间位置时，应力大小及分布规律变化不大(见图10)。

7 结论

在上船过程中，当变截面滑靴一半上船后，滑靴底部垫木及钢板应力变大。这是由于滑靴上部结构物的立柱位置正好在滑靴的中间位置，此时，将会在滑靴和滑道前沿的接触位置，对底部垫木及钢板产生剪切应力，出现应力集中现象。因此，建议滑靴上船快到中间位置时，应让驳船负载，避免桩腿弯矩过大造成破坏。对于拖点，在上船过程中，其应力大小及规律均变化不大。主要原因在于：拖点主要承受拉力作用，上部桩腿传递到拖点的压力对拖点影响较小。变截面滑靴和桩腿连接位置处，在装船过程中，船舶和码头之间的高差发生变化时，应力值和分布规律没有明显变化。主要原因在于：该部位主要承受来自桩腿的压力作用，拖点的水平力对该部位影响较小。