新安江模型中河道汇流方法的改进

2020-06-12李致家臧帅宏刘志雨董鹏飞马亚楠

河海大学学报(自然科学版) 2020年3期

李致家，臧帅宏，刘志雨，徐杰，董鹏飞，马亚楠

(1.河海大学水文水资源学院，江苏南京 210098； 2.水利部水文局，北京 100053；3.烟台市福山区水利局，山东烟台 265500)

新安江模型是由赵人俊[1-2]提出的概念性水文模型，在中国湿润、半湿润地区的降雨径流模拟及预报中得到广泛应用，并取得了良好的效果[3]。目前新安江模型在河道汇流计算中采用的是Muskingum分段连续演算法[4]，一般适用于地势较陡的地区，另外，其中的参数(K、x)没有考虑时间和空间上的变异性，不能随着河道特征以及水力要素的变化而变化，因此有必要对新安江模型河道汇流进行研究，增加新的汇流方案，进一步增强模型的适用范围。

河道流量演算以圣维南方程组[5]为理论基础，利用上断面流量过程演算下断面流量过程。由于圣维南方程的复杂性，目前无法求得其精确解析解，因此在实践中常采用近似的计算方法。目前常用的河道演算方法可分为2种：一种是基于河段水量平衡方程和槽蓄方程的水文学方法，如Muskingum法[6-9]；1938年MCCarthy提出一种原始的“水文”洪水演算方法，即Muskingum法，其中所有的地形特征和河段的水力学特性归为模型的一系列参数。1969年Cunge在Muskingum法的基础上提出了Muskingum-Cunge(MC)演算法[10]，将Muskingum演算法扩展到时间可变参数。1978年Pouce和Yevjevich在Cunge的基础上，考虑到波速的变动问题，建议采用变动参数表示动力波速和水面宽度，提出了变动参数MC方法[11]。但在变动参数的实际应用中存在质量不守恒问题，由此，Todini对变动参数MC模型引入修正因子对模型进行修改，提出Muskingum-Cunge-Todini(MCT)方法[12]。另一种是直接求解完全圣维南方程组或其简化方程组的方法，即水力学法，为水文学方法提供了理论学基础。随着计算机计算速度提高，求解圣维南方程组的速度有了飞速提高，所以基于圣维南方程的各种简化形式也得到了广泛应用[13-15]，例如运动波、扩散波方法。运动波不考虑动力方程中的惯性项和附加比降项，适用于坡度较陡的山区，而扩散波不考虑惯性项，能反映回水影响，可用于平原河网地区[16]，所以扩散波比运动波适用范围更广。

扩散波以及MCT这2种方法可以较好地反映洪水波在河道中的运动特点，2种方法均能够根据河道断面特征及河道的下垫面特征来推求河道断面流量，与现行求解完全圣维南方程组的各种方法相比，这2种演算法解法相对容易，所需资料相对较少。因此，扩散波演算法和MCT方法既能保证计算精度，又便于求解与编程。本文采用这2种方法，同时考虑旁侧入流建立具有物理基础的数字河道汇流模型，将其与原来的新安江模型进行了耦合，对新安江模型进行改进，改进后模型命名为XAJ-DCH模型(Xin’anjiang Digital Channel Model)，并将XAJ-DCH模型应用到呈村流域来验证模型的合理性和适用性。

1 研究流域和数据

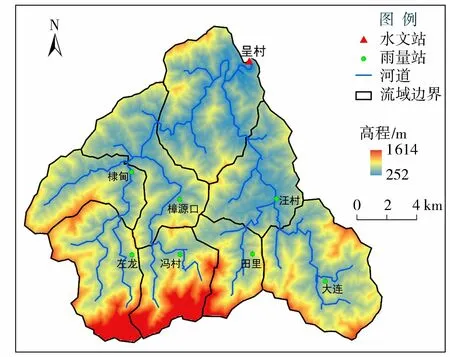
图1 研究流域示意图Fig.1 Map of study catchments

呈村流域位于安徽省黄山市，属于钱塘江流域，邻近中国东南沿海，位于亚热带季风气候区，年平均温度17 ℃，冬季盛行西北风，天气晴冷干燥；夏季多东南风，气温高，光照强，空气湿润；春秋两季气旋活动频繁，冷暖变化大。春季及初夏多锋面雨，夏秋之际多台风，季风环流的方向与主要山脉走向基本正交，山脉起着阻滞北方寒流和台风的作用。年平均降水量1 600 mm，其中4—6月多雨，占50%，易发生洪涝灾害；7—9月，占20%，旱灾频繁。河川径流年内、年际变化较大，是典型的湿润地区。呈村流域洪水具有涨落陡、洪峰高、历时短等特点。呈村流域总面积为298.024 km2，如图1所示，共含有7个雨量站，分别是樟源口、汪村、棣甸、左龙、田里、冯村、大连，1个水文站为呈村站。数字高程资料(DEM)来自美国地质调查局(USGS)免费提供的全球90 m×90 m的原始DEM数据，主要用于填洼、确定流向、水系提取等处理。高程变化范围为262～1 614 m，地势南高北低。

2 模型构建及应用

2.1 河道演算顺序及河道断面概化

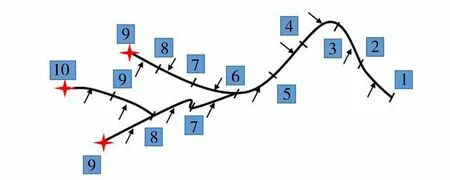
图2 河道计算顺序编码图Fig.2 Sequentially coding diagram of river channel computation

首先在数字高程模型的基础上，利用Arcgis软件提取流域的填洼、流向、汇流累积、水系等，采用自然子流域法划分子流域。首先找到每个子流域的出口点位置，然后根据流向文件确定每个子流域出口点到整个流域出口点之间的河道，这部分河道用于河道演算；将提取的整个流域的出口点设为编号1，按照流向文件，根据D8法原则，从编号为1的栅格开始向上游搜索入流栅格，依次搜索设置编号2，3，…直至各支流河链的起始点，如果在搜索中发现有2个入流栅格，则这2个入流栅格编号相同。如图2所示，编号1为流域出口点，红色星标代表着上游子流域的出口点，在进行河道演算时，从上游栅格最大编号开始计算，寻找每个编号出现的次数，对相同编号的河段依次进行河道演算。本文假设计算河道是矩形河道，同时考虑旁侧入流的影响。河道中每个断面的河宽计算采用Topkapi模型中河宽计算公式[17]在进行河道演算时，根据流向，假设上下游2个栅格的中心点代表河道断面，则两者之间的直线距离就代表该河段之间的距离。

2.2 模拟方法

2.2.1 Muskingum-Cunge-Todini(MCT)方法

MCT方法是在变参数Muskingum-Cunge方法基础上引入校正因子β、校正后的库朗数C*和雷诺数Re来保证计算过程中的质量守恒[10]，计算公式如下：

(1)

(2)

(3)

(4)

O2=C1I2+C2I1+C3O1+C4

(5)

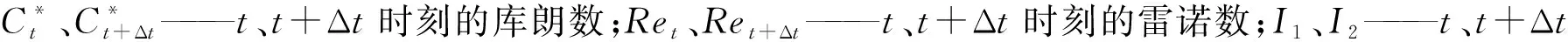
2.2.2 扩散波方法

忽略动力方程中的惯性项，假定河道演算为紊流形式，流量计算采用曼宁公式：

(6)

(7)

式中：Sf——河道摩阻比降；S0——河底比降;h——河道水深,m；Q——河道总流量，m3/s；n——河道的曼宁糙率系数；A——流断面面积，m2；R——水力半径,m。

网格单元k点的河底比降、摩擦比降向前一个网格l点进行向前差分作近似计算，计算公式如下：

(8)

(9)

式中：S0k——河底比降；Sfk——k点的摩擦比降；E——河道底部高程，m；Δx——k、l这2个网格点之间的距离，m。

2.3 子流域与河道匹配问题

实现子流域与计算河道之间的耦合是一个关键问题。在时间尺度上，新安江模型产流计算和坡面汇流计算是以1 h为时间步长，而在用扩散波方法或者MCT方法进行河道演算时，为了保证计算的稳定性条件，是以秒为时间步长，因此涉及一个时间尺度转换的问题，在这里采用的是将1 h的产流量均分。

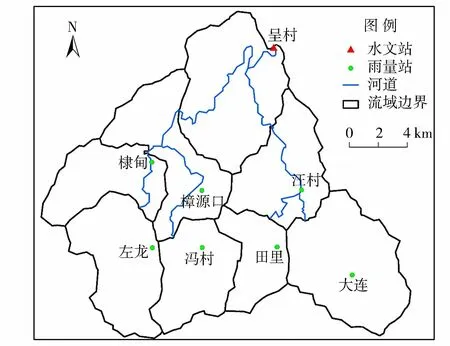
图3 用扩散波方法和MCT方法进行河道演算的河道部分Fig.3 Extracted channel routed by diffusion wave and MCT method

在空间连接上，主要把子流域进行2种划分，第一种是位于计算河道上游的子流域，如图3所示，左龙、冯村、田里、大连这几个子流域，在进行三水源划分之后，用滞后演算法进行子流域河网汇流演算，得到每个子流域出口点的流量，作为起始河段的上游断面的输入流量；第二种是计算河道所在的子流域，如图3所示的棣甸、樟源口、汪村、呈村，这些子流域进行三水源划分之后，根据每个子流域中河道的栅格数量，将水量进行均分，平摊到每个河段中，作为侧向入流。

2.4 模型率定

为检验XAJ-DCH模型的适用性，选取呈村流域的历史洪水进行模拟分析。在选择洪水时保证大、中、小洪水全面选择，并且各种峰形及历时长短的洪水尽量覆盖。为了保证率定参数的准确性，将大约2/3的场次洪水用于参数率定，然后将剩下的进行检验。共选择了1986—1998年共23场洪水进行模拟，前15场用于率定期，后8场用于验证。

3 结果及讨论

3.1 参数率定结果

为保证计算稳定性，扩散波方法河道演算以2 s为时间步长，MCT方法以600 s为时间步长。在使用扩散波方法时，对于一场洪水的模拟基本控制在20 min以内，使用MCT方法时基本控制在2 min以内，所以XAJ-DCH模型可用于实时预报。由表1可以看出，新安江模型中共含有17个参数，而XAJ-DCH模型在此基础上增加了一个河道曼宁糙率系数n。因为2个模型只是汇流模块不一致，所以2个模型除了汇流参数，其他的参数率定值保持一致。河网蓄水消退系数Cs[18]是子流域河网汇流计算中一个极其敏感的参数，反映流域退水速率的快慢。XAJ-DCH模型中扩散波方法的Cs率定值和MCT方法Cs率定值分别为0.896、0.890，两者的Cs率定值相近，而新安江模型中Cs率定值为0.780，比XAJ-DCH模型中所采用的2种方法的Cs率定值偏小。Cs通过影响子流域的河网调蓄作用控制洪峰的形状，n通过影响河道调蓄作用对洪峰形状起控制作用。这2个参数共同对洪峰起控制作用，两者处于相互协调、相互制约的关系。因为采用不同的河道汇流方法对河道调蓄作用也存在着差异，为了达到相同的洪水模拟效果，所以Cs值也会存在差异。

表1 XAJ和XAJ-DCH模型参数率定值Table 1 Calibrated parameters of XAJ model and XAJ-DCH model

注：Ke为流域蒸散发折算系数；Wum为上层张力水蓄水容量；Wlm为下层张力水蓄水容量；C为深层蒸散发折算系数；B为张力水蓄水容量曲线次方；Wm为流域平均张力水蓄水容量；Im为不透水面积占全流域面积的比例；Sm为表层自由水蓄水容量；Ex为表层自由水蓄水容量曲线的指数；Kg为表层自由水蓄水库对地下水的日出流系数；Ki为表层自由水蓄水库对壤中流的日出流系数；Cg为地下水消退系数；Ci为壤中流消退系数；Lag为滞后时间；k为Muskingum法洪水波在河段内传播时间；x为Muskingum法权重系数。

3.2 模型模拟结果分析

根据GB/T 22482—2008《水文情报预报规范》，选择洪量合格率、洪峰合格率、确定性系数以及峰现时间误差4个指标作为评价标准，洪量相对误差及洪峰相对误差不超过20%为合格，确定性系数大于等于0.7为合格，峰现时间误差小于等于3为合格[19]。图4中C1、C2、C3分别代表率定期Muskingum法、MCT方法、扩散波方法的模拟情况，V1、V2、V3分别代表验证期使用原新安江模型中Muskingum法、XAJ-DCH模型MCT方法和扩散波方法的模拟情况。表2列出了采用3种演算方法得到的率定期及验证期所有次洪模拟特征值。图5为呈村1986061909号洪水用以上3种演算方法得到的洪水流量过程线。

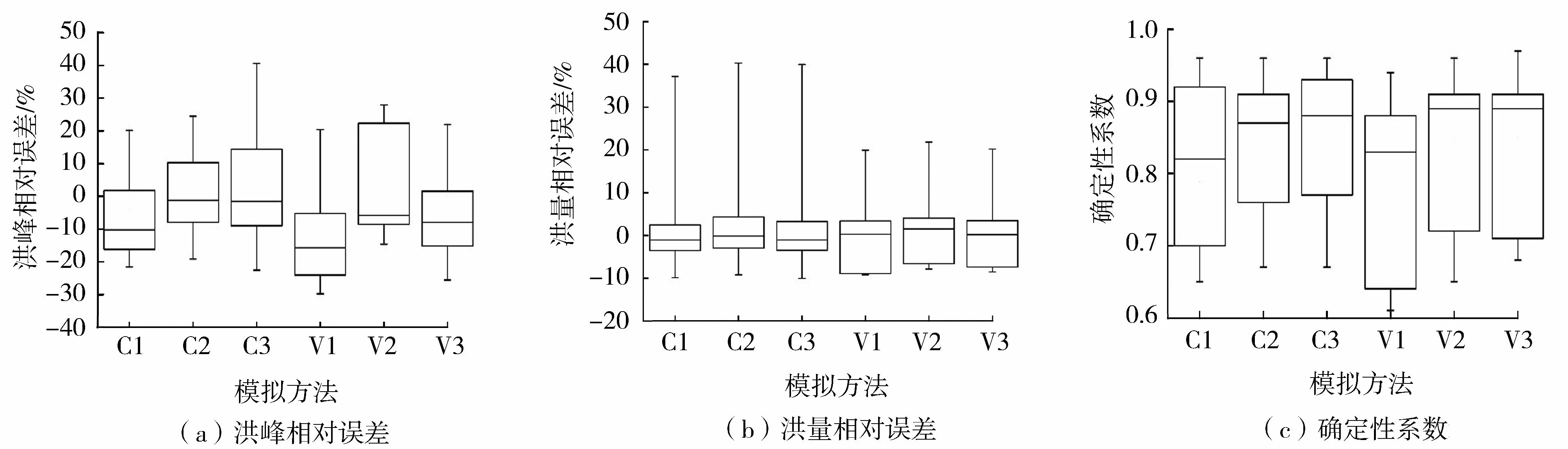
图4 呈村流域洪峰相对误差、洪量相对误差、确定性系数箱线图Fig.4 Box plots of the relative peak discharge error, relative runoff volume error and Nash-Sutcliffe efficiency statistics of all hourly simulations in Chengcun catchment

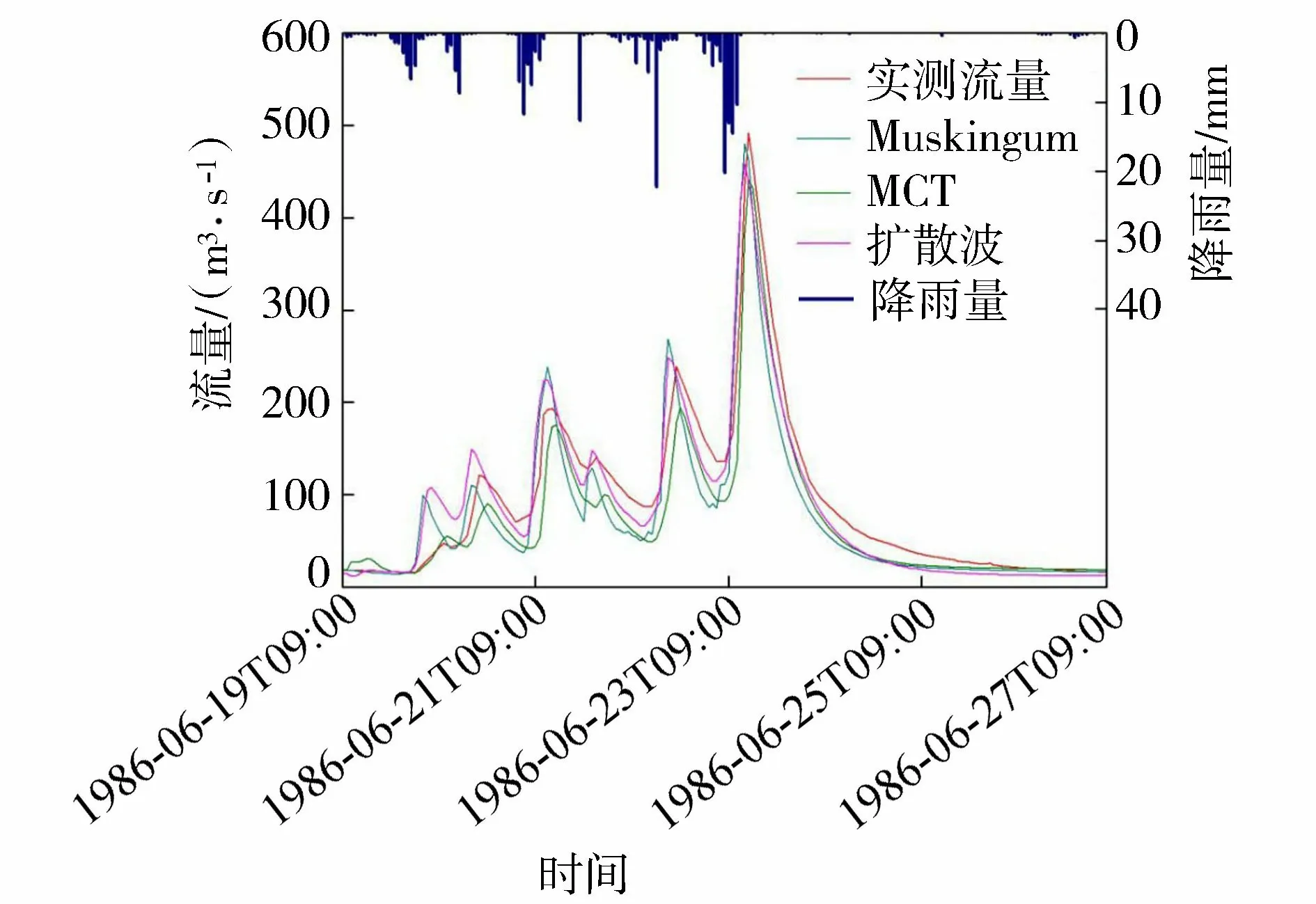
图5 呈村1986061909号洪水过程线Fig.5 Observed and simulated hydrographs of flood No. 1986061909 by using different channel routing methods

表2 次洪模拟结果特征值统计Table 2 Characteristic statistics of the results of flood event simulation %

由图4可以看出，呈村流域率定期和验证期3种演算方法的洪峰相对误差处于-20%～20%之间，洪量相对误差处于-10%～10%之间，确定性系数基本上都大于0.7，并且3种方法的洪峰相对误差、洪量相对误差、确定性系数模拟的结果相似。总体来说，3种方法的模拟结果均在可以接受的范围。

4 结论及展望

4.1 结论

a. 新安江模型中的马斯京根法计算简单，计算效率高，只要有充足的实测资料，通过率定参数可获得良好的模拟效果，但新安江模型没有考虑河道参数的时空变异性。而XAJ-DCH模型中采用的MCT方法和扩散波方法考虑了河道的时空变异性，如河宽、河道坡降、初始水深等，并且XAJ-DCH模型可同时计算出各河道断面的水位和流量。

b. XAJ-DCH模型简单，运行时间短，可用于实时洪水预报。

c. XAJ-DCH模型中加入的扩散波方法考虑了回水的影响，可用于平原地区，适用范围比马斯京根法广。