350 km/h 高速货运动车组载物动力学性能分析

燕春光，邓功勋，温博阁，彭勇

（1.中车唐山机车车辆有限公司，河北唐山063000； 2.中南大学交通运输工程学院，轨道交通安全教育部重点实验室，湖南长沙410075； 3.中车工业研究院有限公司，北京100070）

我国正在研制350 km/h 高速货运动车组[1]. 国外曾直接将高速客运列车改装成货物列车[2]，我国的高速货运动车组将在所有车厢中设置集装器. 与载客动车组不同，货运动车组的轴重较大，且将在已有的高铁线路上运行，而货物的状态属性多样，装载工况将影响列车的行车安全.

研究高速货运动车组的货物—车辆耦合动力学离不开现有的普通铁路货车的研究成果. 货物有液体与固体，其均会影响列车和货物的安全性. Ashtiani 等[3]利用液体晃动数学模型和车辆多体动力学模型，研究了液体装载率对油罐车通过道岔时的行车安全影响. Kolaei 等[4]采用高阶边界元法对部分装载的罐内液体晃动的谱问题进行了研究，分析了纵向及横向激励下的车辆动力学特征. Shi 等[5]提出了一种基于连续介质力学的液体晃动分析方法，并研究了不同速度下铁路罐车的动力学特性. 何华等[6]利用FLUENT 软件计算分析了罐车液体运输的动侧压力，建议在罐车内增设挡波板以减弱罐车内的液体晃动. 刘小民等[7]利用双向流固耦合方法，仿真分析了不同材料防波板在列车制动过程中的受力情况，建议油罐车的装载率避免在0.8 附近. 因此，有必要研究高速货运动车组装载液体货物后的行车动力学响应特征.

固体货物装载也会影响车辆安全性. 我国也提出了重载货物的装载加固规则以保障车辆安全[8]. 彭永昭[9]基于SIMPACK 软件研究了货物质量、重心位置、装载偏移量等对C70H敞车运行安全的影响规律. Zhang 等[10]考虑货物装载时的三维位置，提出了不同线路条件下铁道货车的三维装载安全域. 由此可见，固体货物装载方式也会影响到车辆安全性. 本文考虑未来高速货运动车组出现的流体、固体货物装载工况，利用 LS-DYNA 软件，基于任意拉格朗日-欧拉（Arbitrary Lagrangian- Eulerian，ALE）算法，构建列车-集装器货物流固耦合有限元模型，研究分析货运动车组在不同货物装载工况高速不平稳运行下悬挂状态剧变的车辆及集装器货物耦合动力学行为及安全性.

1 列车集装器货物流固耦合有限元模型

1.1 高速货运动车组有限元模型

高速货运动车组有限元模型基于LS-DYNA 软件构建. 车体结构采用符合TB/T3260.4—2011 标准的不同铝合金材料. 铝合金材料的密度为2 700 kg/m3，弹性模量70 GPa，泊松比 0.29. 而列车车体主要为板梁结构，在有限元建模时可用壳单元表征其结构特性[12]. 对动车组进行网格划分前，需进行几何清理，并删除对计算结果影响不大的部件. 为了准确表征其结构特征，车体有限元的单元网格尺寸控制在50 mm 以内. 自动进行网格划分后，需对局部区域进行网格细化. 列车存在许多对称结构、部件，其在网格划分时，也需采用对称网格以保证有限元模型的结构对称性. 同时，列车车体存在较多的圆角，对于尺寸大于25 mm 的圆角需采用双排或以上网格，尺寸小于25 mm 的圆角可直接采用单排网格. 网格划分完后，需检查网格质量. 车体主要采用壳单元进行建模，需保证单元的雅克比不小于0.7，长宽比小于5. 为提高计算速度，车体采用*MAT_20 号材料卡片模拟.

列车转向架的悬挂参数能显著地影响列车的曲线通过性能及行车安全性能. 高速货运动车组的转向架悬挂参数既不同于350 km/h 系列的动车组，也异于普通铁路货车. 为准确模拟列车钩缓及转向架悬挂参数，主要采用*MAT_119 号材料卡片，以表征其三向的刚度及阻尼特性. 同时，转向架的横向止挡会较大程度上影响列车的曲线通过性能[13]，为准确表征横向止挡的止挡间隙参数，将横向止挡的刚度曲线在止挡间隙范围内设为 0. 同时为了模拟转向架悬挂装置的预压缩，对其在仅受重力作用下进行预仿真模拟.

高速货运动车组为8 编组，为了提高计算效率，仅模拟动车组的头车及第2 节车. 根据货运动车组的研制方案. 最终得到的高速货运动车组的有限元模型如图1 所示. 高速货运动车组有限元模型网格单元数量为2 420 000，节点数量为2 000 000. 按照铁道车辆设备的编号规则，对所有车轮、头车的11 个集装器和2 车的20 个集装器按其从一位端到二位端的顺序进行编号.

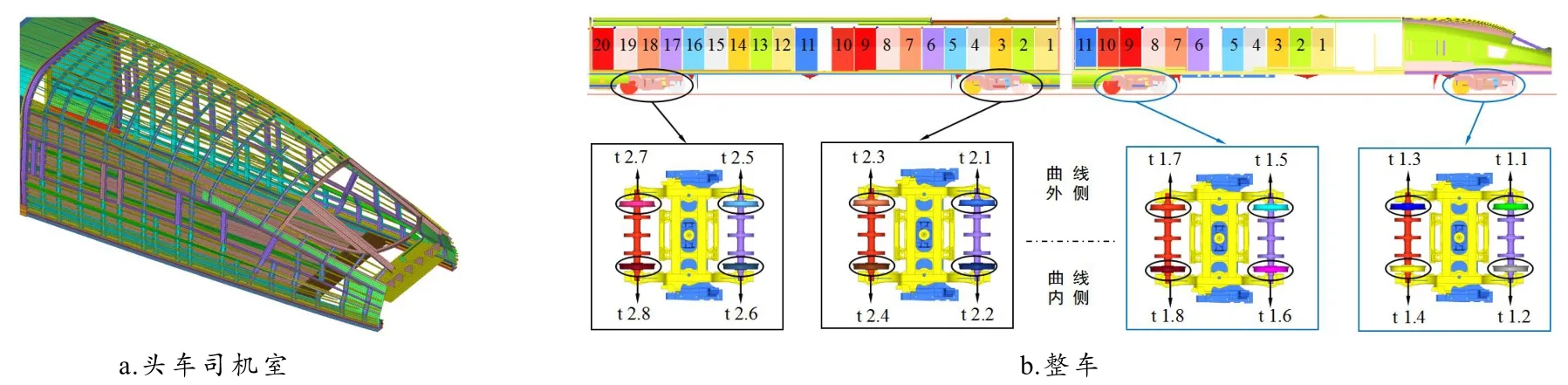
图1 高速货运动车组有限元模型

1.2 集装器货物流固耦合有限元模型

为满足公路、铁路、航空一体化运输要求，考虑货运动车组内部布置空间及列车车门通过尺寸，中车唐山机车车辆有限公司研制了适用于高速货运动车组的大容量集装器. 集装器采用铝合金材料，其空间三维尺寸为2 700 mm × 1150 mm ×2 300 mm ，其自重为205 kg，载重625 kg.

集装器可装载固体、液体等货物. 列车运行时，液体货物不可避免地会在集装器中晃动，导致流体与结构的相互耦合作用即产生流固耦合效应. 本文采用ALE 算法模拟货物的流固耦合. ALE 算法同时用Lagrange（材料）坐标、Euler（空间）坐标及ALE 参考域来描述物质的运动，尤其适用于流体动力学模拟[14]. 根据弹塑性力学理论，材料变形时的应力张量由应力偏量和压力组成：

其中，平均应力为σ0，正比于压强为P；平均应变为 ε0，正比于体积变形为ΔV/V. 对于流体材料，须同时用本构模型和EOS 状态方程描述其材料特性. 本构模型用于描述变形式的应力偏量与应变偏量间的关系，EOS 状态方程用于描述体积变形ΔV/V和压强P 的关系. 本文中用水表示液体，其本构模型和EOS 状态方程分别用*MAT_09 和*EOS_GRUNEISEN 描述，即：

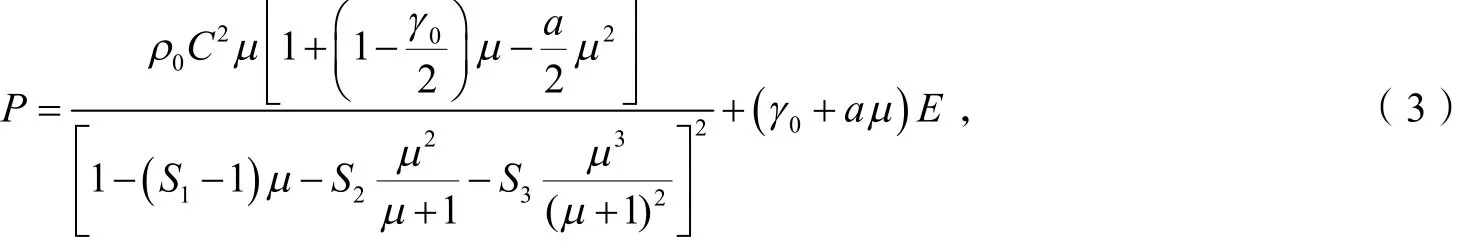
式中，Si( =1,2,3)为速度—压力率曲线的斜率系数，C 为速度—压力率曲线的截距， γ0为Gruneisen常数，a 为μ 和 γ0的一阶体积修正量. 对于液体而言，其在LS-DYNA 中材料参数及状态方程的各个参数如表 1 所示. 此外，为了在 LS-DYNA 中实现流固耦合模拟，还需定义*CONSTRAINED_ LAGRANGE_IN_SOLID 等ALE 流固耦合算法关键字.

表1 液体的材料本构参数及状态方程参数值

1.3 边界条件设定

实际中列车行车环境复杂多变，为研究高速运行条件下列车集装器货物流固耦合动力学响应，本文主要研究货运动车组以350 km/h 不减速通过最小半径曲线的动力学规律，而有限元是一种以直代曲的方法，车轮划分网格后类似于轮对多边形，因此，在不考虑横风环境下，货运动车组以350 km/h不减速通过最小半径曲线可以算作一种极限恶劣工况. 参考我国《高速铁路设计规范》[15]，确定轨道线路模型. 列车运行速度为350 km/h 时，最不利的曲线半径为5 500 km，轨道超高量为169 mm. 两节车厢均考虑为装满所有集装器，但集装器内货物状态及装载率不同. 集装器通过固定爪与列车车体地板固连，本文先假设固定爪不会失效，即先将集装器与车体地板固连，分析其所受到的惯性力是否超过其失效阈值. 轮轨接触模拟为*CONTACT_AUTOMATIC_SURFACE_TO_SURFACE，FS 0.35=，FD 0.32=，并对每个车轮都单独设置轮轨接触以得到所有车轮的轮轨接触力.

2 货运动车组脱轨系数分析

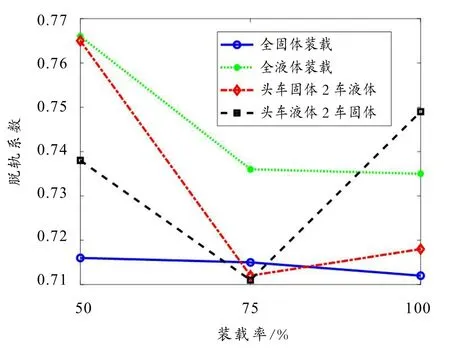
图2 不同工况下货运动车组脱轨系数

轨道车辆运行安全性评价的一个重要指标就是脱轨系数. 货运动车组基于现有的客运高速列车平台开发，因此采用目前的高速动车组的安全指标阈值更为合适. 根据我国《高速动车组整车试验规范》[16]规定，脱轨系数应Q/P≤0.8.

基于列车—线路—集装器货物流固耦合大系统有限元模型，仿真得到高速货运动车组在不同货物装载率及货物状态属性下的脱轨系数峰值的绝对值，如图2 所示.

由图2 可见，不同的货物状态及集装器装载率均会影响列车的脱轨系数. 对于全固体或者全液体货物装载工况，其货物状态最为简单，脱轨系数均随装载率的增大而减小，但是对于两节车固体与液体混合装载的情况，脱轨系数均是随着装载率先减小再增大. 对于50%和75%的中低货物装载率的工况，均是全液体装载时的脱轨系数最大，对于满载时，则是头车液体货物装载第2 节车固体货物装载时的脱轨系数最大. 同时，由于列车以350 km/h 通过半径5 500 m 的曲线是一种恶劣的极限运行条件，导致脱轨系数都比较大，但均没有超过0.8 的安全阈值，表明高速货运动车组以最高设计速度不减速通过最小半径曲线时，无列车脱轨风险.

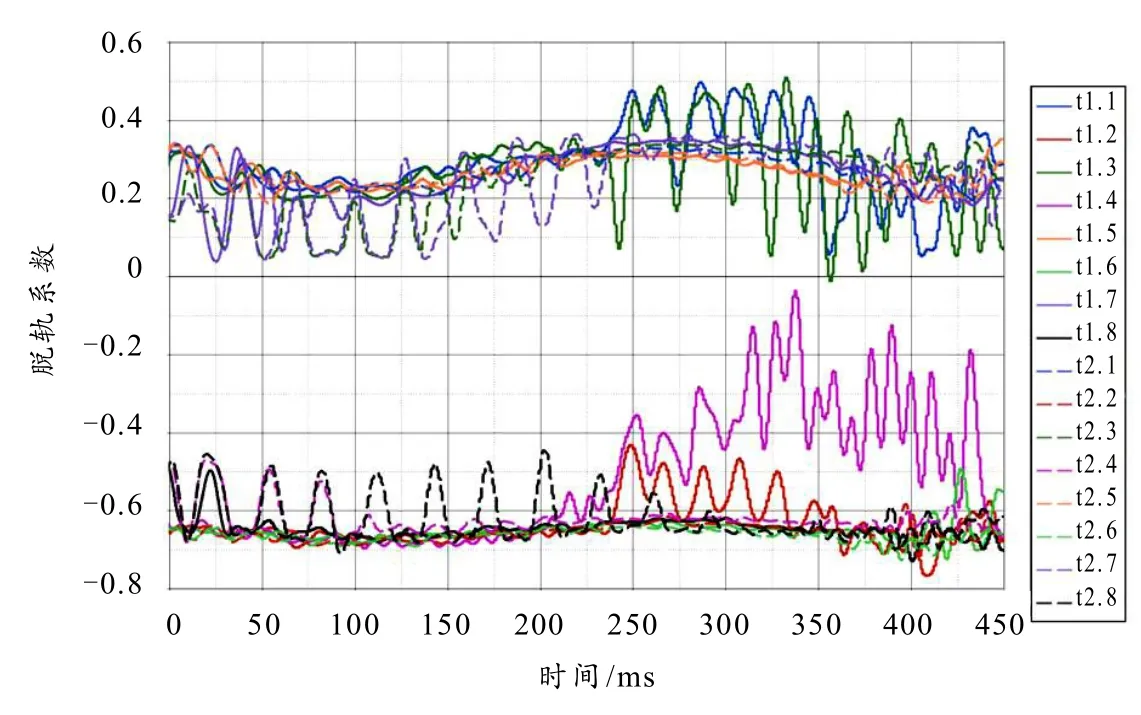
图3 全液体货物50%装载时列车脱轨系数

针对列车脱轨系数最大的工况，单独分析所有车轮的脱轨系数，如图3 所示. 列车车轮按照图1 的顺序编号，其中曲线内侧的车轮编号均为偶数，曲线外侧的车轮编号均为奇数. 可以发现，所有偶数编号即曲线外侧车轮的脱轨系数均为负值，因为曲线外侧的车轮所受的车轮横向力与仿真模型定义的正向相反，而负值的脱轨系数明显大于正值，表明曲线外侧车轮的脱轨系数明显大于曲线内侧，说明列车在5 500 m 最小曲线半径的工况下，此装载工况的列车的重力分力不足以抵抗离心力，使得曲线外侧车轮的脱轨系数明显大于曲线内侧，且各个时刻均为曲线外侧车轮的脱轨系数要大. 同时可以发现头车一位端所有车轮的脱轨系数在240 ms 左右后会出现波动现象，其中一位端第二个轮对车轮（ 1.3t 、 1.4t 号车轮）的脱轨系数波动尤为明显，而2 车二位端最后一个轮对的车轮脱轨系数在240 ms 左右之前出现波动，即货运动车组高速过曲线时，呈现出了脱轨系数的波动从后轮对转移到前轮对的现象. 这与头车的集装器的布置方案有关，头车的前半部分即一位端部分主要为司机室，无货物装载，在高速通过小半径曲线时，出现了部分的轮对负载转移.

3 集装器货物安全性分析

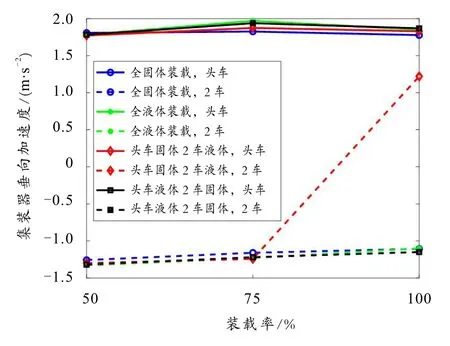
图4 不同工况下集装器的相对垂向加速度

集装器的运动情况将直接影响到货物及集装器固定爪的安全性. 集装器的加速度应小于固定爪的失效阈值. 而集装器固定爪在1 060 kg 载荷的作用下，对固定爪分布施加纵向、横向、垂向5 g、1 g、3 g 的加速度载荷时，未见固定爪失效[1]. 因此，本文以此数值作为集装器固定爪的失效参考阈值.

高速货运动车组不减速通过曲线时，无制动等引起的纵向冲击情况，本文主要分析集装器的垂向加速度. 在所有工况下，集装器相对于列车车体的垂向加速度峰值如图4 所示. 可以发现，所有工况下，集装器相对垂向加速度均远小于固定爪的冲击失效阈值即固定爪无垂向失效风险. 且在不同工况下，头车与第2 节车中的集装器峰值垂向加速度的方向几乎均相反. 各工况下集装器峰值垂向加速度值虽相差不大，但相同工况下头车集装器的垂向加速度始终大于第2 节车中的集装器.

图5 全液体货物50%装载时集装器的相对垂向加速度

对第2 节中脱轨系数最大工况的所有集装器的垂向加速度进行分析，其时间历程如图5 所示. 可以发现，两节车厢中前后位置间的集装器的垂向加速度存在明显差异. 两节车厢中的同一纵向位置集装器垂向加速度的变化规律刚好相反，如位于头车最后面的二位端的11 号集装器与位于第2 节车中的最后面的20 号集装器的垂向加速度变化规律刚好相反，但却与第2 节车中的最前面的1 号集装器的垂向加速度变化规律几乎相同. 而同一节车厢中，前后布置的集装器的垂向加速度变化规律相反，几乎是像关于中间部位集装器呈对称分布，位于车厢中部的头车中5 号集装器及2 车中10号集装器的垂向加速度远小于车厢头尾端集装器的垂向加速度. 这主要是因为列车通过曲线时，存在点头现象，而车辆-货物耦合动力学效应在列车点头运动下直接影响到了前后集装器的点头运动使得前后集装器的垂向加速度方向相反.

4 结论

基于我国正在研制的高速货运动车组，本文采用ALE 算法，构建了列车—线路—集装器货物流固耦合大系统有限元模型，研究货运动车组在不同货物装载工况下高速通过最小半径曲线的动力学安全性能及集装器货物的安全性，并分析集装器之间的动力学响应差异.

不同的货物状态会影响到列车与集装器货物的动力学行为，需采用流固耦合的方法分析液体货物晃动引起的列车及集装器动力学响应差异；不同装载率的货物也会影响到列车与集装器的力学响应及安全性. 货运动车组在不同装载工况下高速通过最小半径曲线时虽无脱轨及固定爪垂向冲击失效风险，但为保证列车及集装器货物安全，应提高集装器的装载率；头车司机室由于其自身结构特征，无法装载货物，使得前后车轮间的脱轨系数差异明显. 而装载货物同时也会影响到列车及集装器的点头等运动学行为，使得前后集装器的力学响应差异明显，车厢中间位置的集装器最为安全. 各车厢中的二位端位置的集装器是在货运动车组行车时应关注的重点.