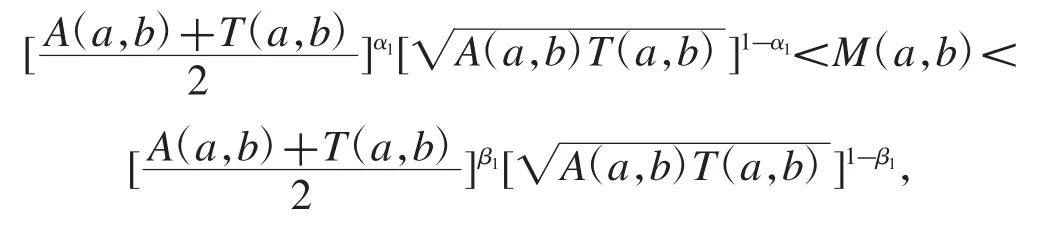关于Neuman-Sándor平均的一个较强上下界估计

何 灯，吴善和

（1.福清第三中学，福建 福清 350315；2.龙岩学院数学与计算机科学学院，福建 龙岩 364012）

0 引言

二元平均之间的比较，一直是不等式研究的一个热点.2003年及2006年，Neuman E与Sándor J在文献[1-2]中定义Schwab-Borchardt平均SB（a，b），该平均可衍生出许多常见的平均，如第一类 Seiffert平均 P（a，b），第二类 Seiffert平均 T（a，b），Neuman-Sándor平均 M（a，b），对数平均 L（a，b）.近几年，Neuman-Sándor平均和其他二元平均得到深入的研究.特别地，从有关Neuman-Sándor平均与其他二元平均或它们的各类组合比较中发现了许多重要的结论，参见文献[1-16].

在现有研究的基础上，笔者对Neuman-Sándor平均M（a，b）的相关结果进行汇总比较，发现算术平均 A（a，b）与第二类 Seiffert平均 T（a，b）能够更精确构造出 M（a，b）的上下界.在此基础上，构造M（a，b）的一类上下界模型，建立M（a，b）的一个较强上下界估计.

1 预备知识

2 引理及证明

3 主要结论及证明

定理得证.

注可见式（4）的强度.

下面提出一个猜想，供有兴趣的读者探究.

猜想双边不等式