遗传算法优化BP神经网络的岩质边坡稳定性预测

黎玺克

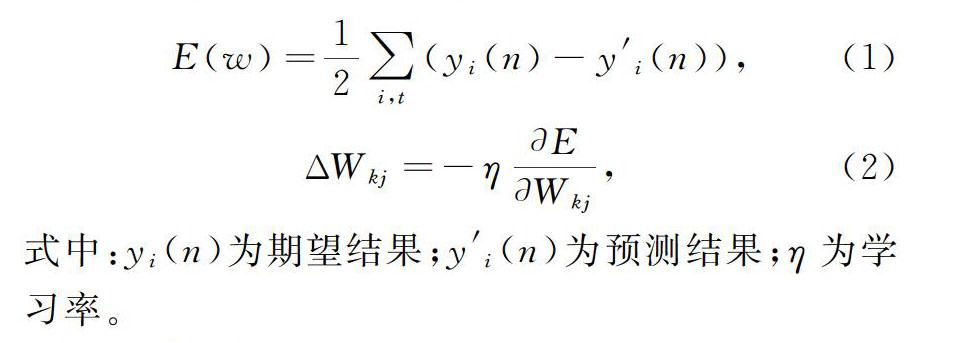
摘要：为了解决边坡工程中非线性变化给稳定性预测造成的困难，建立了GABP神经网络计算模型预测岩质边坡稳定性。采用定性评价和相互作用矩阵复核的方式，选取边坡坡度、边坡高度、斜坡结构类型、岩体强度、控滑结构面倾角、岩体结构特征、地表变形强度、人类活动强度8个评价因子作为BP神经网络的输入变量;利用遗传算法对神经网络的初始权值和阈值进行优化后训练岩质边坡稳定性预测模型;对比分析GABP神经网络和BP神经网络的预测效果。结果表明，优化后的预测结果误差绝对值小于0.15的占85%，未优化的传统神经网络仅占45%，优化后的预测结果更加接近真实值，表明遗传算法对传统BP神经网络的优化是有效的。研究结果对建立岩质边坡稳定性预测模型具有一定的参考价值。

关键词：区域地质学;遗传算法;BP神经神经网络;岩质边坡;稳定性

中图分类号：P694文献标识码：A

doi： 10.7535/hbgykj.2020yx03007

Abstract：

In order to resolve the difficulty of stability prediction caused by nonlinear change in slope engineering， a GABP neural network model was established to predict the stability of the rock slope. Firstly， eight evaluation factors， including slope， height， slope structure type， rock mass strength， angle of sliding control structure plane， rock mass structure characteristics， surface deformation strength and human activity intensity， were selected as input variables of BP neural network by qualitative evaluation and interaction matrix review. Secondly， the initial weights and thresholds of neural network were optimized by genetic algorithm to train the prediction model of rock slope stability. Finally， the prediction effects of GABP neural network and BP neural network were compared and analyzed. Results show that 85% of the optimized prediction error absolute values are less than 0.15， while nonoptimized errors only account for 45% of traditional neural network. The optimized prediction results are more close to the real value which indicates that the genetic algorithm is effective for the traditional BP neural network optimization.

The study can be consulted for establishing prediction models of rock slope stability.

Keywords：

regional geology; genetic algorithm; BP neural network; rock slope; stability

受地形地貌的影响，中国西南地区地质灾害发生频率较高，灾后治理需要耗费大量的人力和物力，灾前防治可有效减少生命财产的损失，因此，对边坡稳定性的预测研究具有重要的意义[1]。

传统的研究方法通常把影响边坡稳定性的因子量化后独立代入模型进行物理分析，然而在实际边坡工程实践中，各变量相互作用构成一个微观和宏观上连续非线性变化的复杂的巨型系统，简化模型将影响分析结果精度。人工神经网络的出现很好地解决了这个问题，通过模拟生物神经元的结构特征和作用机理，解决边坡系统中的非线性问题。已有学者将岩土工程学科和计算机学科相结合，寻求解决边坡问题的新方法[25]。冯夏庭等[6]利用BP神经网络对96个圆弧和锲体破坏边坡实例训练学习，建立边坡安全系数预测模型;李兴等[7]通过神经网络算法调整模糊逻辑系统的参数，对高速公路边坡进行危险性评价;鲜木斯艳·阿布迪克依木等[8]将MIV理论和神经网络算法结合绘制龙南县滑坡易发区间图;李骅锦等[9]以黑方台95处滑坡为研究对象，运用迭代BP神经网络算法寻求不同影响因素的内在联系及其与滑距的关系;冯非凡等[10]将神经网络算法应用在滑坡敏感性評价中，为了避免BP神经网络陷入局部极小值，采用粒子群算法优化其权值和阈值。

笔者从2018年贵州省地质灾害排查数据中选取73处岩质边坡作为实验样本，随机抽取53组训练样本和20组测试样本，通过定性分析和相互作用矩阵复核的方式选取8个评价因子，采用遗传算法（genetic algorithm，GA）对多层前馈式误差反向传播网络算法（bakepropagation，BP）的初始权值和阈值优化后训练岩质边坡稳定性预测模型，用测试样本检验模型的准确性，研究结果可为岩质边坡稳定性预测提供参考价值。

1基本原理

1.1BP神经网络

BP神经网络是一种具有自学习和自适应能力的人工神经网络模型，由输入数据的前向传播和误差值的反向传播两部分组成。标准的神经网络拓扑结构包含输入层节点、隐含层节点、输出层节点，层与层各节点相互连接，同一层各节点互不作用。该算法将研究对象n个样本X=（x1，x2，…，xj，…，xn）作为神经网络的输入层节点，期望结果Y=（y1，y2，…，yi，…，yn）作为相应的输出节点，通过相应的权值和阈值进行计算，比较预测结果与实际结果可得到误差值，见式（1），适应度函数是衡量误差值是否符合要求的标准，对不满足要求的计算结果网络将在权向量空间运用梯度下降法进行误差反向传播，其中隐含层和输出层每一步权值的修正量，见式（2），通过反复迭代，使误差达到期望值，完成BP神经网络计算模型的建立[1112]。

1.2遗传算法优化BP神经网络

传统的BP神经网络采用误差函数的梯度下降法，因为学习率的不可知性和权值及阈值的随机性，算法在寻找到局部最优解时就停止计算，不利于建立正确的网络模型，同时，隐含层的层数和节点数也直接影响网络模型的学习效果，层数过多，计算过程缓慢，隐含层节点数过多易造成网络模型过度学习，隐含层节点数过少易造成片面学习，BP神经网络的局限性影响计算结果的效率和精度，笔者采用遗传算法对其进行优化。

遗传算法以“优胜劣汰”的自然法则为基础，通过选择、交叉、变异3种自然界进化的方法，建立一种自动搜索全局最优解的计算模型，它可以克服BP神经网络在（-1，1）区间自动生成初始权值和阈值的随机性，使网络模型更加准确。该算法首先随机产生初始种群作为第1代，采用实数编码规则，将权值和阈值编入个体的染色体中，根据适应度函数评判每一代个体的优劣性，采用比例选择法使适应度函数低的优秀个体更易遗传到下一代，然后通过交叉操作，子代在遗传父代优良基因的基础上重组得到新的个体，更加适应环境变化。为了保证个体的多样性，变异是进化过程中的关键步骤，它不仅可以使个体趋于最优解时加快收敛速度，也可以使算法陷入局部最优解时跳出局部，搜索全局最优，避免算法未成熟先收敛，通常设定较小的变异概率指导变异操作执行，最后判断个体是否满足适应度函数，若满足条件，遗传算法终止，将进化后的优秀个体即初始权值和阈值代入BP神经网络中进行仿真训练，得到网络模型[1314]。

2应用实例

2.1选取评价因子

自然界中不确定因素众多，边坡作为一个复杂的系统，其稳定性受多种因素影响，本研究秉承代表性、整体性、可取性的原则，从边坡的几何特征、边坡结构特征、边坡影响因素3个方面选取边坡坡度（P1）、边坡高度（P2）、斜坡结构类型（P3）、岩体强度（P4）、控滑结构面倾角（P5）、岩体结构特征（P6）、地表变形强度（P7）、人类活动强度（P8）8个影响因素作为边坡稳定性的评价因子。

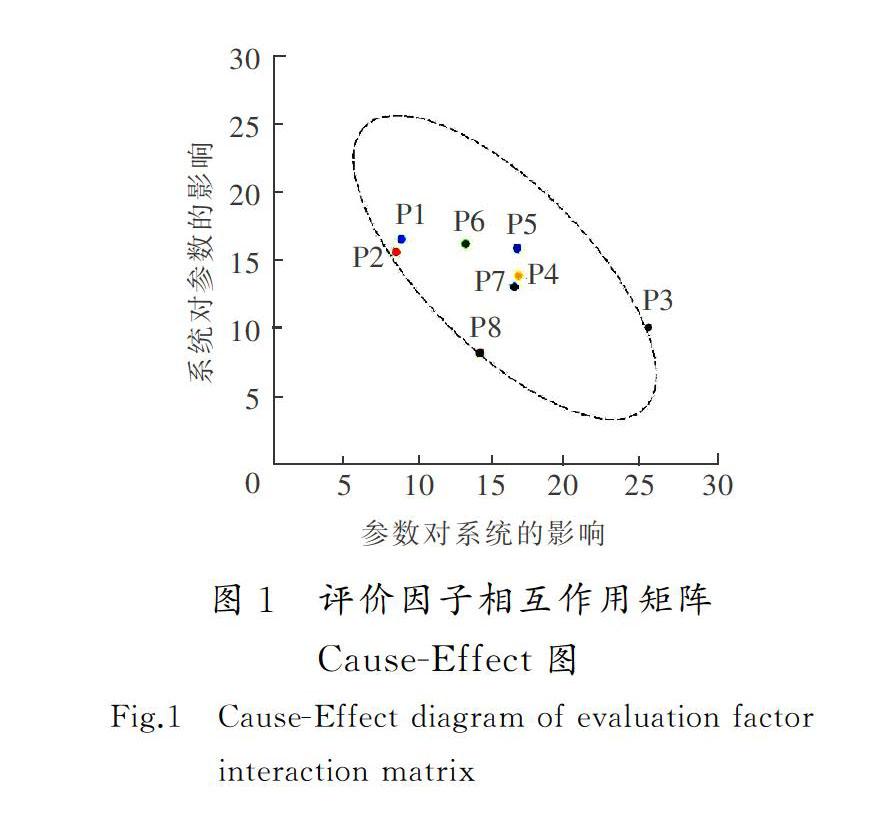
为了验证评价因子选取的正确性，在定性评价的基础上建立相互作用矩阵进行复核。相互作用矩阵可考虑各个变量相互作用对整个边坡稳定性系统的影响，研究结果具有代表性。首先根据半定量专家取值法对相互作用矩阵进行赋值计算，选取10位從事地质工作的专业人员对该矩阵进行评估打分，取有效数据的平均值计算，计算结果可绘制

评价因子相互作用矩阵CouseEffect图（如图1所示）。从图1可以看出，数据点集中分布在C=E的垂直线上，表明选取的8个评价因子对边坡稳定性的影响大，进行边坡稳定性分析时应该全部考虑这8个评价因子[15]。

2.2选取数据

从2018年贵州省地质灾害排查数据中选取73处具有代表性的岩质边坡作为实验样本，其中稳定状态为稳定、较稳定、基本稳定、不稳定的样本数量分别为17处、18处、18处、20处，从总样本集中随机抽取53组训练样本和20组测试样本，输入参数为前文确定的8个评价因子，由于计算模型输入层的特殊性，需要将定性评价结果量化，在查阅大量文献的基础上，结合研究区域地质环境特征，建立如表1所示评价因子量化规则。

2.3确定模型参数

根据经验公式与试算法确定隐含层节点数为17，建立8171三层神经网络拓扑结构，其中BP神经网络的参数包括：训练次数为1 000次，学习速率为0.1，训练目标为0.001;遗传算法优化的参数包括：迭代次数为50次，种群规模为25，交叉概率为0.25，变异概率为0.06。

2.4实验结果与分析

为了展现遗传算法对BP神经网络的优化作用，将GABP神经网络和BP神经网络2种模型的预测结果对比，如图2所示，可以看出遗传算法优化后的模型预测效果明显优于传统BP神经网络。

绘制2种模型预测结果与期望结果的误差曲线，如图3和图4所示。从图中可知，BP神经网络预测结果误差较大，最大误差为0.279 9，优化后的算法误差较小，最大误差为0.181 3。从表4可以看出，20个测试样本在传统BP神经网络预测的结果中，误差绝对值小于0.15的占45%，而遗传算法优化后的预测结果绝对值小于015的占85%，明显高于优化前的算法，所以GABP神经网络对BP神经网络的优化是成功的。

3结语

1）传统的BP神经网络因其初始权值和阈值的随机性以及自身算法的局限性，计算结果易陷入局部最优解，模型泛化能力不强，遗传算法具有“优胜劣汰”的算法特点，可以优化初始权值和阈值，两者结合可以充分发挥算法优势，提高模型的准确性。

2）以贵州省73处典型岩质边坡作为实验对象，选取53组样本作为训练集，20组样本作为测试集，对比BP神经网络和GABP神经网络的预测结果，发现遗传算法优化后的BP神经网络预测效果更佳，误差绝对值小于0.15的样本数达到85%，明显高于相同条件下传统BP神经网络的样本数（45%）。实验结果表明遗传算法对BP神经网络的优化是有效的。

3）在今后的研究中，可进一步扩大样本集，提高模型对样本的学习效果，训练更加完善的岩质边坡稳定性预测模型。

参考文献/References：

[1]黄润秋，向喜琼，巨能攀.我国区域地质灾害评价的现状及问题[J].地质通报，2004，23（11）：10781082.

HUANG Runqiu， XIANG Xiqiong， JU Nengpan. Assessment of Chinas regional geohazards： Present situation and problems[J]. Geological Bulletin of China， 2004，23（11）：10781082.

[2]任庆国，苗兰弟.支持向量机模型在断层破碎带围岩变形预测中的应用[J].河北工业科技，2017，34（3）：194201.

REN Qingguo， MIAO Landi. Application of support vector machine model in fracture zone surrounding rock deformation prediction[J]. Hebei Journal of Industrial Science and Technology， 2017，34（3）：194201.

[3]翟會君，翟亚锋，朱涛，等.基于回归ELM神经网络模型的滑坡变形及失稳预测模型[J].河北工业科技，2017，34（6）： 440447.

ZHAI Huijun， ZHAI Yafeng， ZHU Tao， et al. Prediction model of landslide deformation and instability based on regressionELM neural network model[J]. Hebei Journal of Industrial Science and Technology， 2017，34（6）： 440447.

[4]樊玉敬， 钱龙， 刘硕，等. 雷达岗滑坡形成机理及稳定性分析[J]. 河北工业科技， 2013，30（2）：6365.

FAN Yujing， QIAN Long， LIU Shuo， et al. Formation mechanism and stability of Leidagang landslide[J]. Hebei Journal of Industrial Science and Technology， 2013，30（2）：6365.

[5]史笑凡，杨春风，王可意.基于支持向量机和改进BP神经网络的路基边坡稳定性研究[J].公路交通科技，2019，36（1）： 3137.

SHI Xiaofan， YANG Chunfeng， WANG Keyi. Study on stability of roadbed slope based on SVM and improved BP neural network[J].Journal of Highway and Transportation Research and Development， 2019，36（1）： 3137.

[6]冯夏庭，王泳嘉，卢世宗.边坡稳定性的神经网络估计[J].工程地质学报，1995，3（4）：5461.

FENG Xiating， WANG Yongjia， LU Shizong. Neural network estimation of slope stability[J]. Journal of Engineering Geology， 1995，3（4）：5461.

[7]李兴，张鹏.基于模糊神经网络的高速公路边坡危险性评价与防护策略[J].公路工程，2018，43（5）：305309.

LI Xing， ZHANG Peng. Risk assessment and protection strategy of expressway slope based on fuzzy neural network[J].Highway Engineering， 2018，43（5）：305309.

[8]鲜木斯艳·阿布迪克依木，何书.基于MIVBP神经网络的滑坡易发性空间预测[J].人民长江，2019，50（11）：140144.

ABUDIKEYINU XMSY， HE Shu. Spatial prediction on landslide vulnerability based on MIVBP neural network[J]. Yangtze River， 2019，50（11）：140144.

[9]李骅锦，许强，何雨森，等.甘肃黑方台滑坡滑距参数的BP神经网络模型[J].水文地质工程地质，2016，43（4）：141146.

LI Huajin， XU Qiang， HE Yusen， et al. BP neural network model for analyzing the impact factors of the travel distance of the Heifangtai landslide in Gansu[J].Hydrogeology and Engineering Geology， 2016，43（4）：141146.

[10]冯非凡，武雪玲，牛瑞卿，等.粒子群优化BP神经网络的滑坡敏感性评价[J].测绘科学，2017，42（10）：170175.

FENG Feifan， WU Xueling， NIU Ruiqing， et al. Landslide susceptibility assessment based on PSOBP neural network[J]. Science of Surveying and Mapping， 2017，42（10）：170175.

[11]李灿，周海清，宋强辉.基于BP神经网络的客土喷播边坡侵蚀模数预测模型研究[J].粉煤灰综合利用，2019（3）：812.

LI Can， ZHOU Haiqing， SONG Qianghui. Rsesarch on prediction model of erosion modulus of guest soil spraying slope based on BP neural network[J]. Fly Ash Comprehensive Utilization， 2019（3）：812.

[12]闵江涛，杨杰，马晨原.基于改进GABP网络算法的边坡力学参数反演分析[J].水电能源科学，2019，37（11）：152155.

MIN Jiangtao， YANG Jie， MA Chenyuan. Back analysis of slope mechanics parameters based on improved GABP network algorithm[J].Water Resources and Power， 2019，37（11）：152155.

[13]臧焜巖，李梅红.基于GABP模型的露天矿边坡稳定性预测[J].中国矿业，2019，28（6）：144148.

ZANG Kunyan， LI Meihong. Slope stability prediction of openpit mine based on GABP model[J]. China Mining Magazine， 2019，28（6）：144148.

[14]戴妙林，屈佳乐，刘晓青，等.基于GABP算法的岩质边坡稳定性和加固效应预测模型及其应用研究[J].水利水电技术，2018，49（5）：165171.

DAI Miaolin， QU Jiale， LIU Xiaoqing，et al. Study on GABP hybrid algorithmbased prediction model and its application to rock slope stability and reinforcement effect[J]. Water Resources and Hydropower Engineering， 2018，49（5）：165171.

[15]赵建军，贺宇航，黄润秋，等.基于因子分析法的边坡稳定性评价指标权重[J].西南交通大学学报，2015，50（2）：325330.

ZHAO Jianjun， HE Yuhang， HUANG Runqiu， et al. Weights of slope stability evaluation indexes based on factor analysis method[J]. Journal of Southwest Jiaotong University， 2015，50（2）：325330.