基于Fluent的波节管内流体流动与传热特性研究

邓小叶 彭培英 朱海荣 卢红亮

摘要：为了深入研究影响波节管传热效果的主要因素，应用CFD软件Fluent对波节管内流体的流动和传热特性进行数值模拟，分别研究了不同入口流速v（0.3，0.5，0.7和0.9 m/s）、波峰直径D1（28，30，32，34和36 mm）、弧形段长S1（34，23，17，13和10 mm）下波节管内流体的流动与传热特性。结果表明，不同型号波节管的努塞尔数（Nu）、流体压力损失以及综合性能随着入口流速的增加而增加;随着波峰直径D1（弧形段长S1）的增大，波节管的Nu先增大后减小，最后趋于一个相对稳定的值。当波节管的波峰直径D1=34 mm时，波节管的传热性能最好，流体压力损失最大，综合性能最好;弧形段长S1=23 mm时，波节管的换热性能最佳，流体压力损失最大，综合性能最好。通过参数正交分析可知，影响波节管传热效果的因素由强到弱依次为入口流速v、波峰直径D1、弧形段长S1。研究成果可为工程实际中提高波节管传热性能提供理论指导。

关键词：工程传热、传质学;波节管;Fluent;数值模拟;传热特性;正交分析

中图分类号：TK11文献标识码：A

doi： 10.7535/hbgykj.2020yx03002

Abstract：

In order to study deeply the main factors influencing the heat transfer effect of corrugated tubes， CFD software Fluent was used to simulate the fluid flow and heat transfer performance. The flow and heat transfer performances of corrugated tubes under the conditions of different inlet velocities v（0.3 m/s， 0.5 m/s， 0.7 m/s， 0.9 m/s）， peak diameters D1（28 mm， 30 mm， 32 mm， 34 mm， 36 mm）， and arc lengths S1 （34 mm， 23 mm， 17 mm， 13 mm， 10 mm） were studied respectively. The results show that the Nusselt number， the pressure drop and the comprehensive performance of different types of corrugated tubes increase with the inlet velocity. The Nusselt number increases firstly and then decreases with the peak diameter D1 （arc section length S1）， and finally remains as a relatively stable value. The heat transfer performance of corrugated tubes is the best at the peak diameter D1 of 34 mm， and the Nusselt number is the largest at the length of arc section S1 of 23 mm. Meanwhile， the pressure drop is the largest and the comprehensive performance is the best under the two abovementioned conditions. Through the parameter orthogonal analysis， it can be concluded that the order of the factors influencing the heat transfer effect of corrugated tubes from strong to weak is as follows： inlet velocity v， peak diameter D1， and arc length S1. This study can provide theoretical guidance for improving the heat transfer performance of corrugated tube in engineering.

Keywords：

engineering heat and mass transfer; corrugated tube; Fluent; numerical simulation; heat transfer performance; orthogonal analysis

換热器作为一种主要的换热设备，广泛应用于化工、能源、石油、农业和电力部门中。提高换热设备的换热效率可以有效地降低成本、节约资源。波节管凭借其良好的换热性能在众多异形强化管中脱颖而出，将它应用于换热器中，可以大大提高换热设备的换热效率。由于波节管中流体的流动与传热性能对波节管的换热效果影响较大，因此，研究波节管中流体的流动与传热性能及其主要影响因素是十分必要的。

波节管是20世纪90年代，由中国东北大学学者郎逵[1]提出并研制的，它是由相互交替变化的弧形管段和直管段组成，工业上由光管液压工艺胀形而成。自提出至今，已有不少研究人员对波节管内流体流动、传热特性以及结构设计等方面进行了研究。马小晶等[2]利用数值模拟的方法对5种不同尺寸波节管内流体的流动和传热特性进行了分析。张伟玮等[3]通过实验研究、理论校核和数值模拟相结合的方法，研究波节形状对波节管稳定性和传热特性的影响。韩勇等[4]利用kε模型针对外凸波节管、内凹波节管以及波纹相间波节管内流体的流动和传热特性进行了数值研究，比较3种波节管在不同雷诺数下的流动和传热综合性能。陈秀平等[5]利用遗传算法和数值模拟结合的方法对层流情况下的波节管进行波形优化。徐建民等[6]对波节管的性能进行数值模拟，并通过实验验证发现在湍流状态下，管内的努塞尔数比光管高 1.86～2.17 倍，并且当雷诺数为15 000 时强化换热效果最好。汪威等[7]对波节管中脉冲流动的换热效果进行模拟研究，分析了脉冲流动对换热效果的影响。韩怀志等[8]对氦气在波节管内的传热特性及阻力特性进行研究，分析了波距和波谷半径对波节管的传热特性以及阻力特性的影响。苏勇俊等[9]、张艾萍等[10]对波节管内的流动传热特性进行了数值模拟和场协同分析。金铁石等[11]对波节管高效换热元件中纵向逆流换热的传热特性和阻力特性进行了数值模拟，研究了不同波距及雷诺数产生的影响。付金辉[12]对光管、不同结构的螺旋波节管及波节管进行数值模拟，比较了螺旋波节管与波节管在流动与传热特性方面的不同。韩怀志等[1314]对一种新型的非对称外凸式波节管进行数值模拟研究，并与传统的对称型外凸式波节管进行比较，分析了两者流动及传热特性的区别。LI等[15]通过数值模拟方法对盘旋螺旋波节管进行了研究，分析了螺旋波纹参数和雷诺数对流动和热传递的影响，并将流场和温度场与螺旋波节管中的流场和温度场进行了比较。LAM等[16]对流体横掠波节管时的流动情况进行了大涡模拟。在对雷诺数为300、波节间距为1.136～3.333 m的模型进行流场、尾流结构和阻力系数及升力系数的分析，发现波节管存在一个临界点。LAOHALERTDECHA等[17]对水平光滑管和波节管内的传热系数和压降进行了实验研究。研究表明波间距对波节管内的传热系数和压降有显著的影响。ASHMAWY[18]研究了表面粗糙度对波节管内耦合应力流体的流速和平均流速的影响。KAOOD等[19]利用数值模拟的方法研究了不同波纹方向（内、外）和波纹形状（三角形、曲线、矩形和梯形）对横向波节管内湍流的热和水力特性的影响。

为了深入研究影响波节管内流体流动和传热特性的因素，本文数值模拟了不同入口流速v、不同波峰直径D1以及不同弧形段长S1时波节管内流体的流动与传热过程，设计参数正交分析并且对结果进行讨论，得出各个参数对波节管内流体流动和传热特性的影响规律。

1物理模型

波节管的几何模型如图1所示，其主要参数包括：弧形段长S1，直管段长S2，波距S（其中S=S1+S2），管壁厚σ，波峰直径D1，基管直径D2（如图2所示）。本文研究的波节管结构尺寸如表1所示，在数值计算过程中不考虑波节管管体的内外径和壁厚，以及波节管内部的热传导。

2网格模型

本文采用非结构化网格的方法，网格单元为正四面体，全局尺寸为0.3，在壁面进行加密，壁面处网格尺寸第1层为0.03，从壁面处的增长率为1.2。图3为4#波节管的网格模型示意图，经过网格无关性验证后可确定最后的网格数为561 603。

3数学模型

3.1控制方程

依据波节管的特点，在模拟时参考文献＼[9＼]作出以下假设：

1）不考虑重力因素;

2）管内的流体属于不可压缩流体，且充分进行湍流流动;

3）边界无滑移，则连续性方程、动量方程以及能量方程如下

考虑到假设波节管內流体流动为完全湍流，并且其分子黏性影响的因素可以忽略，故选用标准kε湍流模型，其计算收敛性和准确性都非常符合工程计算的要求，具有较高的稳定性、经济性和计算精度。

3.2边界条件

1）入口：设定为VELOCITY INLET，速度大小分别为0.3，0.5，0.7，0.9 m/s，速度方向垂直于入口边界，设置流体为冷却水，冷却水的温度为283 K。

2）出口：将出口边界条件设定为OUTFLOW。

3）壁面边界条件：将壁面边界条件设定为WALL，忽略壁厚的影响，壁面的温度设置为353 K。

3.3求解设置

本文的流体介质为水，属于不可压缩流体，因此采用基于压力的求解器（Pressure Based）、稳态（Steady）、隐式格式求解，选择标准kε湍流模型。在求解控制设置中，同时启动湍流方程、流动方程和能量方程。压力速度耦合方式采用SIMPLE算法，对流项均采用二阶迎风格式。

4结果与讨论

4.1波节管内流体流动特性分析

图4为光管与4#波节管的速度云图对比，如图4 a）所示，流体在光管内的流动很简单，没有周期性扰动，因此流速没有波动，所以换热性能较低。而图4 b）中4#波节管的速度云图显示：流体在进入波节管时存在“入口效应”，流体要经过4～6个波节之后速度才变得稳定，流体流动呈现周期性变化。

图5为4#波节管局部速度矢量图。分析发现：在波节管的主流段，流体流动速度比较快且速度变化不明显。波节管内流体在充分换热阶段的速度场呈现出周期分布的特点，即管内流体随着波节管流道截面的扩张、收缩而在管内呈现周期性的扰动，所以其速度的分布也呈周期性变化。流体由“直管段”流入“弧形段”时，随着流道截面的扩张，压力增大，速度减小，流体速度等值线向下凹陷;当流体流过波峰，流道截面逐渐收缩，压力减小，流速增大，速度等值线向上凸起;当流体从弧形段流出再次进入直管段，流体不再受截面的影响，将保持这一流速直至进入下一个波节，因此在直管段处的速度等值线基本与轴线相平行，并且存在速度较大的“红色区域”。在波节管的弧形段区域，流体波峰内流动形成了速度很小的“回流死区”，可见波节管的换热性能是优于直管的。

4.2波节管内流体传热特性分析

4.2.1v对波节管内流体传热特性的影响

通过图6中4#波节管在不同入口流速时的温度云图对比，可以发现波节管内流体温度的变化从上游区域到下游区域也存在分层现象，流体温度依次升高，在下游区域，温度的升高幅度相对较大。随着v的增大，管内流体温度升高加快，当v=0.9 m/s时，速度分层现象出现的最早，温度升高最快。

如图7所示，对比各型号波节管在不同v下的努塞尔数（Nu）的变化可以发现，在本文所研究的速度范围内，各型号波节管的Nu均随着v的增大而增大，说明流体流速的增加提高了波节管的换热效果。在其他条件不变的情况下，流体流速的增加，使得热管壁在单位时间内接触到的冷流体量增大，因此强化了管壁的传热效果。

在提高波节管的入口流速后，波节管的Nu增加的同时，波节管内流体流动阻力也有所增大。从图8压力损失随入口流速的变化图中可以发现：在光管中，压力损失随着入口流速的增加从100 Pa左右增加到了500 Pa左右。与光管进行比较，波节管的压力损失要高于光管。压力损失增大，波节管内流体流动阻力会增大，流体流动阻力增大也会提高流体的传热性能。所以波节管相对于光管来说强化换热效果更好，而且在本文研究范围内，流速增大，换热效果也会提高。由于随着流速的增加，换热效果提高，流体流动阻力增加，因此随着流速的增加，波节管的综合性能会提高。由此可见，提高流体流速是改善固定型号波节管传热性能的最简单有效的方法。

4.2.2D1对波节管内流体传热特性的影响

图9为不同波峰直径D1下波节管的温度云图，图10为Nu随波峰直径D1的变化曲线图。综合两图可以发现：D1相同时，v越大，Nu也越大。在不同的入口流速下，波节管的Nu随D1的变化趋势大致相同：当D1<34 mm时，Nu随着D1的增大而增大，而当D1>34 mm时，Nu随着D1的增大而减小，直至趋于一个稳定值。D1=34 mm时，波节管的换热效果最好。这说明，波峰直径D1并不是越大越好，合适尺寸波峰的存在会改变管道中流体的流场分布，强化管壁的传热效果;波峰直径过大则可能导致流体回流不好，形成“回流死区”，反而削弱了管壁的传热效果。

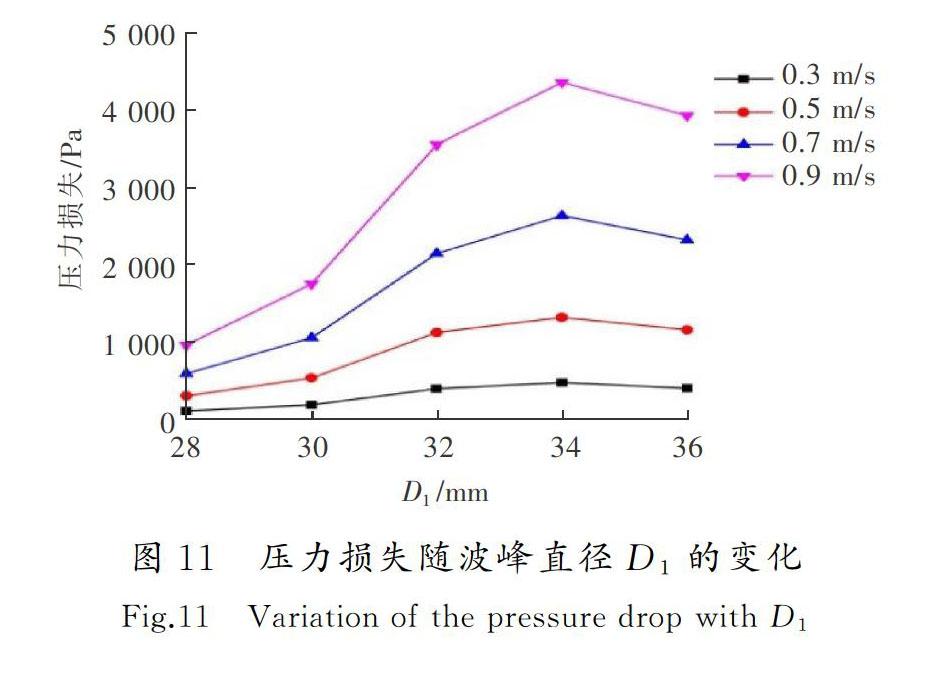
通过图11可以发现，压力损失随波峰直径D1的变化出现先增大后减小的趋势，这与Nu随波峰直径D1的变化趋势是相同的。在本文研究范围内，当波峰直径D1=34 mm时，压力损失最大，流体流動的阻力最大，因此换热效果最好。通过以上的对比可知，当波峰直径D1=34 mm时，波节管的综合传热性能最好。

4.2.3S1对波节管内流体传热特性的影响

图12为不同弧形段长S1下波节管内流体的温度云图，图13为Nu随弧形段长S1的变化曲线图。分析发现：在不同流速下，波节管的Nu随弧形段长S1的变化趋势基本一致，当10 mm≤S1≤23 mm时，Nu随着S1的增大而增大，并在S1=

23 mm时取得最大值;当23 mm

图14为压力损失随弧形段长S1的变化，当弧形段长S1相同时，随着流速的增加，压力损失增大，流体流动阻力增加。随着S1的增大，压力损失呈现先增加后减小的趋势，当S1=23 mm时，压力损失最大，流体流动阻力最大，换热效果最好。当S1>23 mm时，波节管弧形段的弧度减小，流体流动的阻力也随之减小，换热效果也逐渐减弱。结合Nu随弧形段长S1的变化，可以得知，弧形段长S1=23 mm时，波节管的综合性能最好，当弧形段长S1增加到一定值时，压力损失会趋于稳定，流体流动阻力也会趋于平稳。

波节管强化传热的性能是通过调整弧形段长S1和波距S的大小以改变对流体扰动的强弱而实现的。波节管各个波节单元均由弧形段和直管段组成，其实真正起到强化传热作用的是弧形管段。当波峰直径D1为定值时，改变弧形段长S1，波节管的强化传热性能将会受到不同程度的影响。当S1很小时，虽然由于流道截面剧烈变化使得对流体的扰动增强，但在一个“波节单元”中起强化作用的弧形管段太短，影响了波节管的传热性能;增加S1就相当于增加了“波节单元”中起强化作用的管段，所以Nu也随之增大。而当S1过大时，虽然强化管段较长，

但由于流道截面变化相对平缓，从而导致漩涡对主流流体的扰动减弱，影响波节管的传热性能，因此随着S1的进一步增加，波节管的Nu开始回落并最终趋于稳定值。

4.3参数正交分析

利用参数正交分析了解入口流速v、波峰直径D1、弧形段长S1对波节管内流体传热过程的影响。参数正交分析设计方案和结果如表2所示。

在表2所列的9组试验里，可以发现第8组的壁面平均换热系数最大，其水平组合为A3B2C1。因此，本试验各因素的组合中的最优组合为A3B2C1。

各参数的敏感性分析结果见表3。

由表3可知，入口流速v对壁面的平均换热系数影响最大，波峰直径D1次之，弧形段长S1对平均换热系数的影响最小。由此可见，调整入口流速v可以迅速改善波节管的换热性能，同时在实际操作中也简单易行。

5结语

1）在本文的研究范围内，入口流速v越大，波节管的换热性能越好，流体流动阻力最大，综合性能最好。

2）在本文研究的入口流速范围内，波节管的Nu均随着弧形段长S1、波峰直径D1的增加呈现先增大后减小的趋势。当D1=34 mm时，波节管的换热效果最好，流体流动阻力最大，综合性能最好。当S1=23 mm时，波节管的换热性能最佳，流体流动阻力最大，综合性能最好。

3）通过参数正交分析可知，影响波节管壁面传热效果的因素由强到弱依次为入口流速v、波峰直径D1、弧形段长S1。

4）本文未考虑波节管内流体的流动过程伴随着能量损失和阻力性能的变化，因此在最小能量损失和阻力下研究流体输运和热量交换是未来波节管的研究方向。

参考文献/References：

[1]郎逵. 波节管换热器的设计[J]. 节能，1995，155（6）：3841.

[2]马小晶，胡申华，闫亚岭. 波节管强化传热的三维数值模拟分析研究[J]. 水力发电，2012，38（1）：8790.

MA Xiaojing， HU Shenhua， YAN Yaling. Three dimensional numerical simulations on enhanced heat transfer of corrugated tube[J]. Water Power， 2012， 38（1）： 8790.

[3]张伟玮，韩聪，韩怀志，等. 波节形状对波节管结构稳定性和传热特性的影响[J]. 哈尔滨工业大学学报，2013，45（7）：5762.

ZHANG Weiwei， HAN Cong， HAN Huaizhi， et al. Effect of shape on structural stability and heat transfer characteristics of corrugated tubes[J]. Journal of Harbin Institute of Technology， 2013， 45（7）：5762.

[4]韩勇，王定标，张灿灿，等. 3种类型波节管的强化传热模拟分析[J]. 郑州大学学报（工学版），2014，35（6）：1418.

HAN Yong， WANG Dingbiao， ZHANG Cancan，et al.

Numerical comparative study on three types of corrugated tube[J].

Journal of Zhengzhou University（Engineering Science），2014，35（6）：1418.

[5]陈秀平，刘巍，胡明启，等. 基于遗传算法的层流情况下波节管波形优化[J]. 工程热物理学报，2019，40（3）：661667.

CHEN Xiuping， LIU Wei， HU Mingqi， et al. Shape optimization of corrugated tube in laminar flow based on genetic algorithm[J]. Journal of Engineering Thermophysics， 2019， 40（3）： 661667.

[6]徐建民，王晓清，李强. 波节管流动和换热性能的数值模拟及试验研究[J]. 节能技术，2008，26（2）：112115.

XU Jianmin， WANG Xiaoqing， LI Qiang. Numerical simulation and experiential research for fluid flow and heat transfer in corrugated tubes[J]. Energy Conservation Technology， 2008，26（2）： 112115.

[7]汪威，喻九陽，杨侠. 波节管脉冲流强化对流换热数值分析[J]. 武汉工程大学学报，2010，32（3）：8991.

WANG Wei， YU Jiuyang， YANG Xia. Numerical analysis on convection heat transfer in a corrugated tube[J]. Journal of Wuhan Institute of Technology， 2010， 32（3）： 8991.

[8]韩怀志，李炳熙，何玉荣. 波节管管内氦气流动与传热的计算及分析[J]. 华北电力大学学报（自然科学版），2012，39（1）：5963.

HAN Huaizhi， LI Bingxi， HE Yurong. Calculation and analysis of helium flow and heat transfer characteristic in corrugated tube[J]. Journal of North China Electric Power University （Natural Science Edition）， 2012， 39（1）： 5963.

[9]苏勇俊，杨俊保，肖军. 波节管管内流动传热特性的三维数值模拟[J]. 节能，2012，31（8）：1719.

SU Yongjun， YANG Junbao， XIAO Jun. Three dimensional simulation of flow and heat transfer characteristic inside the nodal tube[J]. Energy Conservation， 2012， 31（8）： 1719.

[10]张艾萍，夏荣涛，徐志明，等. 基于场协同理论的强化管换热效果分析[J]. 化工机械，2016， 43（1）：97101.

ZHANG Aiping， XIA Rongtao， XU Zhiming， et al.  Analysis of strengthening heat transfer effects based on field synergy theory[J]. Chemical Engineering & Machinery， 2016， 43（1）： 97101.

[11]金铁石，付崇彬. 波节管纵向逆流换热性能的三维数值模拟研究[J]. 节能技术，2012，30（3）：212215.

JIN Tieshi， FU Chongbin. 3D numerical simulation investigation of heat transfer performance for vertical countercurrent flow in corrugated tube[J]. Energy Conservation Technology， 2012， 30（3）： 212215.

[12]付金辉.螺旋波节管管内外流体流动与传热的数值模拟[D]. 哈尔滨：哈尔滨工业大学，2018.

FU Jinhui. Numerical Simulation of Flow and Heat Transfer of Fluid in TubeSide and ShellSide of Helical Corrugated Tube[D]. Harbin： Harbin Institute of University， 2018.

[13]韩怀志，李炳熙，何玉荣，等.非对称型外凸式波节管内的传热和流动特性[J]. 化工学报，2013，64（6）：19161924.

HAN Huaizhi， LI Bingxi， HE Yurong， et al. Heat transfer and flow characteristics in asymmetric outward convex corrugated tube[J]. CIESC Journal， 2013， 64（6）： 19161924.

[14]HAN Huaizhi， LI Bingxi， YU Biyong， et al. Numerical study of flow and heat transfer characteristics in outward convex corrugated tubes[J]. International Journal of Heat and Mass Transfer， 2012， 55（25）： 77827802.

[15]LI Yaxia， WU Jianhua， WANG Hang， et al. Fluid flow and heat transfer characteristics in helical tubes cooperating with spiral corrugation[J]. Energy Procedia， 2012， 17： 791800.

[16]LAM K， LIN Y F. Large eddy simulation of flow around wavy cylinders at a subcritical Reynolds number[J]. International Journal of Heat and Fluid Flow， 2008， 29（4）： 10711088.

[17]LAOHALERTDECHA S， WONGWISES S. The effects of corrugation pitch on the condensation heat transfer coefficient and pressure drop of R134a inside horizontal corrugated tube[J]. International Journal of Heat and Mass Transfer， 2010， 53（13/14）： 29242931.

[18]ASHMAWY E A. Effects of surface roughness on a couple stress fluid flow through corrugated tube[J]. European Journal of Mechanics/B Fluids， 2019， 76： 365374.

[19]KAOOD A， ABOUDEIF T， ELTAHAN H， et al. Numerical investigation of heat transfer and friction characteristics for turbulent flow in various corrugated tubes[J]. Proceedings of the Institution of Mechanical Engineers， 2019， 233（4）： 457475.

[20]喻九陽，徐建民，郑晓涛，等.列管式换热器强化传热技术[M]. 北京：化学工业出版社，2013.