n-度中心度与k-压力中心度及其并行算法

饶东宁，林卓毅，魏 来

（1. 广东工业大学 计算机学院，广东 广州 510006；2. 香港大学 经济与金融学院，中国 香港 999077）

网络中心度及其并行算法设计实现是网络研究的热点。顶点的网络中心度[1]是对顶点在网络中的重要性的量化。数据随科技发展呈指数增长[2]，网络的规模也日渐庞大。单机已难以实现大规模网络的存储和计算，多机分布式存储[3]与并行计算[4]逐渐成为发展趋势。因此，对网络的研究重点不仅在于网络中心度的研究，还在于网络计算的并行算法设计实现。

目前网络中心度并行算法的设计和实现尚未完善。在提出新的网络中心度时，研究者通常只实验于小型网络，没有考虑在大型网络的应用及并行算法的设计实现。此外，现有的并行算法实现较为分散，只有部分实现方法由Spark框架(https://spark.apache.org/)的GraphX模块提供。使用中心度进行网络分析研究时，需要额外开销来寻找其他中心度的并行算法实现。

本文设计基于Spark的网络中心度并行工具包，并提出n-度中心度和k-压力中心度及其并行算法。在设计并行工具包时，对度中心度和压力中心度进行补充拓展，提出n-度中心度和k-压力中心度。设计其并行算法并借助Spark框架的Pregel方法实现。通过BoardEx(https://corp.boardex.com/)社交网络进行实验测试性能，结果显示设计实现的并行算法有明显的并行加速效果。最后，把并行算法的实现方法与现有的11种网络中心度计算方法，整合成一个基于Spark框架的并行工具包。

1 相关工作

对网络的研究一方面在于提出全新的网络中心度，或综合已有的度量提出加权中心度。Singh等[5]提出综合考虑顶点在图中的全局和局部重要性的图论傅里叶变换中心度(GFT Centrality)。Medeiros等[6]提出基于准最短路径的介数中心度(ρ-Geodesic Betweenness Centrality)，在计算介数中心度的时候不仅考虑最短路径，还加入以ρ作为阈值的准最短路径。饶东宁等[7]提出针对BoardEx金融社交网络的加权中心度，验证各公司的首席技术官和首席信息官的加权中心度与人员所在公司规模的相关性。王露等[8]基于网络拓扑结构综合全局信息和局部信息，提出加权的网络中心度。

另一方面，对网络的研究还在于网络计算的并行算法研究。乔少杰等[9]提出基于Spark的大规模网络社区并行发现算法，能处理更大规模更复杂的网络，运行时间及准确率比Hadoop平台有所提高。Ma等[10]在标签传播算法(Label propagation algorithm，LPA)的基础上提出基于概率和相似性的并行标签传播算法(Probability and similarity based parallel label propagation algorithm，PSPLPA)，借助Spark的Pregel算法实现并行化，相较传统LPA效果更好速度更快。艾川等[11]借助Spark平台，实现超大规模网络传播计算实验算法，可高效进行大规模复杂网络中的信息传播仿真。

2 网络中心度定义

网络可用图G = (V, E)表示，其中V和E表示顶点集和边集。顶点的网络中心度衡量顶点在网络中的重要性。对度中心度进行补充拓展，提出n-度中心度；受介数中心度(Betweenness Centrality)[1]与k-介数中心度(k-Betweenness Centrality)[12]的启发，对压力中心度进行补充拓展，提出k-压力中心度。

2.1 传统网络中心度

2.1.1 度中心度(Degree Centrality)

度中心度[1]是以顶点的度作为网络中心度。度(Degree)是一个顶点在网络中邻居顶点的数量，在有向图中可分为入度(In-Degree)和出度(Out-Degree)。度中心度用式(1)表示。

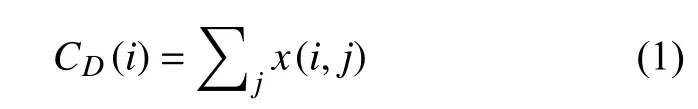
式(1)中，CD(i)表示顶点i的度中心度，x(i,j)表示顶点i和顶点j(i≠j)的连接关系，如有连接为1否则为0。

2.1.2 压力中心度(Stress Centrality)

顶点的压力中心度[13]是其他顶点两两之间最短路径通过该顶点的路径数。压力中心度反映信息在网络中传递时顶点承受的压力大小，表示为

式(2)中，CS(i)表示顶点i的压力中心度，ρst(i)表示顶点s到顶点t经过顶点i的最短路径数。

2.2 n-度中心度和k-压力中心度

2.2.1 n-度中心度(n-Degree Centrality)

n-度中心度是顶点在n度内可以连接的顶点数量，也是与顶点距离不超过n的顶点数。在有向图中也可分为n-入度(n-In-Degree)和n-出度(n-Out-Degree)。相比度中心度只考虑顶点的邻居顶点数量，n-度中心度还考虑到邻居顶点以外n度以内的拓扑结构，通过更大的区域判断顶点的重要性，消除度中心度的局限性。n-度中心度用式(3)表示。

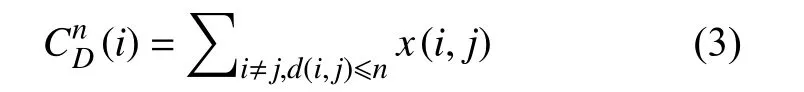
2.2.2 k-压力中心度(k-Stress Centrality)

k-压力中心度是其他顶点两两之间长度不超过k的最短路径通过该顶点的路径数。k-压力中心度反映信息在网络中传递时(传递距离不超过k)，顶点承受的压力大小。在社交网络中，有效的人际关系距离不远。加入信息传递距离的限制，k-压力中心度比压力中心度更适用于社交网络，更好地反映个人在人际网络中传递信息的能力。k-压力中心度为

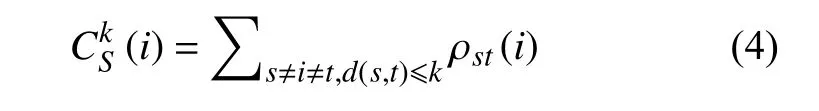
3 并行算法设计与实现

基于Pregel的计算机制分别设计n-度中心度和k-压力中心度的并行算法，并通过Spark框架的Pregel API完成算法实现。

3.1 Pregel

Pregel[14]是一种用于图的迭代计算的并行计算模型。计算面向顶点，顶点有活跃或非活跃两种状态。每轮迭代称为一个超步，包括顶点处理(vprog)，消息发送(sendMsg)和消息合并(mergeMsg) 3个过程。在一个超步中，(1) 顶点接收到上一超步邻居顶点发送来的不同消息，把所有消息通过mergeMsg合并为一条消息；(2) 顶点的属性与合并后消息由vprog处理，可能会更新属性；(3) 更新了属性的顶点处于活跃状态，只有活跃的顶点才会通过sengMsg向所有邻居顶点发送消息。

每次迭代重复步骤(1)～(3)，直到所有顶点都处于非活跃状态即没有新消息产生，或迭代达到设定的最大迭代次数，迭代终止。

3.2 n-度中心度的并行算法

基于Pregel的计算机制，n-度中心度的并行算法设计见算法 1。算法流程解释如下：

(1) 初始化，把顶点集合(点集)作为顶点属性，用以存放可达顶点；

(2) 发送消息，把源点可达但终点不可达的顶点集合，从源点发送到终点；

(3) 合并消息，所有接收到的点集合并、去重，形成一个点集；

(4) 顶点处理，消息的点集与属性的点集合并，更新属性，加入的顶点是距离增加1后新增的可达顶点。

Algorithm 1. n-Degree Centrality algorithm Input: Original graph, n.Output: Computed graph.1. // Initialization 2. for all vertex v∈vertices do 3. create a vertex set S with v in it； 4. end for 5. // Pregel 6. while new messages are produced or iteration do not reach n times do 7. // Send message 8. for all edge e∈edges do 9. send the difference-set between S of source vertex and S of destination vertex to destination vertex；10. end for 11. // Merge message 12. for all vertex v∈vertices do 13. merge messages into a unique-set as msg；14. end for 15. // Vertex program 16. for all vertex v∈vertices do 17. add all vertices of msg to S；18. end for 19. end while 20. // Centrality computation 21. for all vertex v∈vertices do 22. count the vertices number in S；23. end for 24. return computed graph.

初始化后，重复(2)(3)(4)，直到迭代次数到达n时迭代终止。统计各顶点属性中可达顶点数量，即为n-度中心度。

3.3 k-压力中心度的并行算法

基于Pregel的计算机制，k-压力中心度的并行算法设计见算法 2。算法流程解释如下：

(1) 初始化，顶点的属性设置为映射关系(Map)，其中key为顶点，value为key顶点到本顶点的最短路径(用顶点序列表示)集合；

(2) 发送消息，把源点已记录但终点未记录的顶点及最短路径集合，从源点发送至终点；

(3) 合并消息，所有消息中，对于同一顶点只保留路径长度最短的集合，如果有多个则合并成一个集合；

(4) 顶点处理，消息中的所有路径在尾部附上当前顶点，再把顶点和路径集合合并至本顶点属性的Map中。

初始化后，重复(2)(3)(4)，直到迭代次数到达k时迭代终止。所有最短路径筛选出长度大于2的，并去除路径两端顶点，通过统计各顶点出现次数，得出k-压力中心度。

Algorithm 2. k-Stress Centrality algorithm Input: Original graph, k.Output: Computed graph.1. // Initialization 2. for all vertex v∈vertices do 3. create a map with v as key, S(P(v)) as value； 4. // P is shortest-path represented by a vertex list, // S is a set of shortest-paths. 5. end for 6. // Pregel 7. while new messages are produced or iteration do not reach k times do 8. // Send message 9. for all edge e∈edges do 10. send sub-map of source vertex that the keys are not in the map of destination vertex to destination vertex；11. end for 12. // Merge message 13. for all vertex v∈vertices do 14. if path lengths of a key are different then 15. keep the shortest paths and remove others；16. else 17. merge paths into S of the key；18. end if 19. end for 20. // Vertex program

?

3.4 并行算法的实现

n-度中心度和k-压力中心度的并行算法通过分布式框架Spark[15]的Pregel API实现。Pregel API调用方法如下。

Pregel. apply(graph, initialMsg, maxIterations,activeDirection) (vprog, sendMsg, mergeMsg)

其中，initialMsg是初始消息以供初始化；maxIterations是用户设置的最大迭代次数；activeDirection是消息发送方向；vprog，sendMsg，mergeMsg分别是用户自定义的顶点处理，消息发送，消息合并3个函数。将并行算法的顶点处理，消息发送，消息合并3个过程，以及自定义的初始消息和最大迭代次数传入Pregel API，即可完成并行算法的实现。

4 性能测试

对n-度中心度和k-压力中心度的并行算法实现进行实验，测试算法并行加速效果。

4.1 实验环境

使用Spark集群进行实验。集群环境包括各机器的CPU、内核数、分配内存及硬盘等配置，如表1所示。

4.2 实验数据

实验数据源自金融社交网络数据库BoardEx。BoardEx记录商业人士间的联系及各自的个人信息，企业间的联系及企业的详细信息。按美国、英国、欧洲和其他国家各地区划分，每个地区分别有个人网络和企业网络。BoardEx数据库中均是大规模社交网络，其中企业网络相比个人网络规模较小。实验选用英国地区的企业网络，测试n-度中心度和k-压力中心度的并行算法性能。该网络有45 185个顶点，80 418条边。

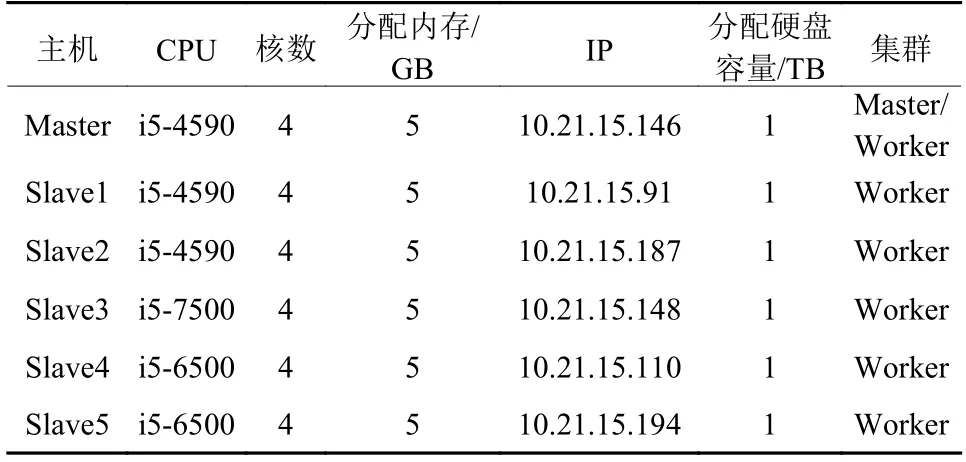
表 1 Spark集群配置Table 1 Spark cluster configuration

4.3 实验设计

使用算法加速比[16]测试两种算法的并行加速效果。算法加速比由式(5)表示。

4.4 实验结果

实验一使用英国企业网络测试n-度中心度并行算法的加速效果。实验结果如图 1所示，展示在不同规模的集群下n-度中心度并行算法的加速比。结果表明n-度中心度并行算法通过拓展集群具有良好的加速效果，在6机集群下加速比均超过3。而随着迭代次数增加(增加n)，加速效果下降。主要原因是消息随迭代次数的增加而变长，导致合并消息和顶点处理的时间开销更大。

图 1 n-度中心度并行算法加速效果Fig.1 Speedup of n-degree centrality parallel algorithm

实验二使用英国企业网络测试k-压力中心度并行算法的加速效果。实验结果如图 2所示，展示在不同规模的集群下k-压力中心度并行算法的加速比。结果表明k-压力中心度并行算法通过拓展集群也有一定的加速效果，但效果不如n-度中心度并行算法。推测原因是算法使用更复杂的消息类型，机器内存受限导致频繁进行垃圾清理，而清理的时间无法通过并行加速。同样的，随迭代次数增加算法的加速效果下降，但不及n-度中心度并行算法加速效果下降得明显。

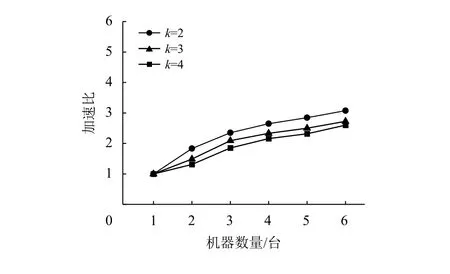
图 2 k-压力中心度并行算法加速效果Fig.2 Speedup of k-stress centrality parallel algorithm

5 网络中心度并行工具包设计

把各种网络中心度的并行算法实现整合成一个网络中心度并行工具包。除了本文设计实现的n-度中心度和k-压力中心度的并行算法，工具包内还包含以下中心度算法的实现：

(1) 改良的接近中心度(Closeness Centrality)与介数中心度(Betweenness Centrality)的并行算法实现；

(2) 饶东宁[17]等提出的并行最小割(Minimal Cut)算法；

(3) 廖志军[18]提出的分布式K-Core算法；

(4) Spark框架的GraphX模块提供的度、PageRank和三角计数(Triangle Count)的方法。

方法(1)也按第4节的步骤进行了性能测试，也表现出一定的并行加速效果；(2)(3)(4)的方法经验证在工具包中可运行。工具包的可行性与拓展性得以验证。网络中心度并行工具包中各方法，包括方法名与方法描述，详见表2。

6 总结

本文将现有的网络中心度并行算法的实现整合成一个并行工具包。在工具包的设计过程中，对度中心度和压力中心度进行补充拓展，提出n-度中心度和k-压力中心度。对两种新度量分别基于Pregel的计算机制设计并行算法，并通过Spark框架的Pregel方法实现。通过BoardEx数据库的社交网络测试并行算法的性能，结果显示均有较好的加速效果。并行工具包提供便捷可拓展的中心度并行计算，工具包内的网络中心度计算方法可通过拓展集群提高计算效率。并行工具包能为网络中心度的研究提供选择，未来的工作将加入更多网络中心度的并行算法，或对工具包内算法加以改进。

表 2 网络中心度并行工具包的方法Table 2 Functions in the network centrality parallel toolkit