一种基于质点弹簧模型的牙龈软组织形变仿真算法

李晋芳，韦光扬，何汉武，蔡嘉鸿，陈基荣

（1. 广东工业大学 机电工程学院，广东 广州 510006；2. 广东工贸职业技术学院 机电工程学院，广东 广州 510510）

虚拟现实技术(Virtual Reality，VR)的应用集中于虚拟手术、远程医疗系统、医学教育等方面。其具有许多优点，可以提高训练效率，有效降低手术训练成本，减少一些当代教学实践带来的负面影响[1-2]。

在虚拟手术的众多研究中，软组织形变建模是其核心。常见的软组织有皮肤、肌肉、神经、血管、黏膜等。虽然它们在结构上差异明显，但是力学特点相似，都涉及复杂生物力学[3]，在力的作用下会发生形变，表现出明显的非线性。

牙龈是指紧贴于牙颈周围及邻近的牙槽骨上淡红色的结构，由复层扁平上皮及固有层组成，是一种典型的软组织。牙龈软组织血管丰富，呈淡红色，坚韧而有弹性，直接与骨膜紧密相连，是口腔黏膜的一部分，一般根据牙龈的厚度可分为薄型和厚型两种。虚拟口腔手术中牙龈软组织的建模仿真研究主要抓住牙龈的这几个特点制定相应的技术方案。

有限元法和质点弹簧模型是当前软组织建模的两种重要的建模方法[4-5]。有限元法在拥有较少的材料参数时也可以描述某一个物理系统，然而运算量较大，实现起来较困难，耗时较长[6-7]，尤其是对复杂的场景，所耗费的时间和计算机内存是相当大的，因此它不适用于虚拟切割这类实时性要求高的仿真。

相比有限元法，质点弹簧模型由于无须连续参数化，既可以用于静态分析，也可以用于动态分析，建模简单、计算速度较快、去除和增加点的操作较容易实现[8]。另外，如果整个模型顶点都被计算会造成计算量巨大和不符合实际，离碰撞点远的软组织区域变化不大，尤其是牙龈软组织。

因此本文提出一种基于质点弹簧模型的适用于牙龈软组织的算法，算法只对碰撞点附近的网格顶点进行更新计算，能够在保证软组织形变符合要求的前提下减少计算量，提升求解精度和系统稳定性。此外，本文通过仿真模拟验证所提出算法的处理效果。

1 牙龈软组织的物理建模

1.1 质点弹簧模型

质点弹簧模型是一种常用的软组织物理建模方法。主要思想是把仿真对象用质点离散化，质点之间用符合线性弹性模型的弹簧连接而成，质点除受弹簧的弹力作用外，弹簧产生的阻尼力与速度成比例关系[9]。

质点弹簧模型如图1所示，网格的边界和节点由质点和弹簧组成，一个弹簧连接两个质点，而一个质点可以连接多个弹簧，这些弹簧是线性的，遵循胡克定律[10-11]。质点在受到外力时，产生的外力作用传递到相邻质点，相邻质点接着传下去带动其相邻质点运动，变形由质点运动产生。软组织形变仿真需要利用数值解算的方法求解形变的动力学模型[12]。

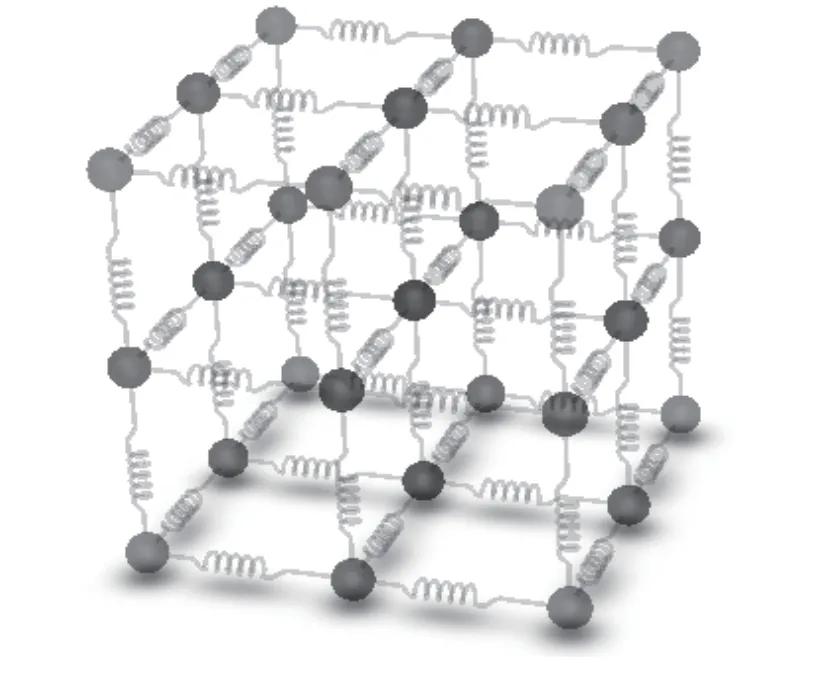
图 1 质点弹簧模型Fig.1 Mass-spring model

质点弹簧模型运算效率高且易于编程实现，能很好地满足虚拟口腔手术的实时性要求[13]，展示牙龈软组织的粘弹性、塑性和非线性等特性的存在。

1.2 一般的数值求解方法及对比

在基质点弹簧模型的虚拟口腔手术系统中，形变仿真的时间步长直接决定了虚拟手术的实时性[14]，选取合适的时间步长是保证牙龈软组织形变精度和实时性的必要前提。求解质点弹簧模型常用的数值求解方法主要有显式欧拉算法、隐式欧拉算法、Runge-Kutta算法等。

为验证各算法的精度分析，本文通过MATLAB以步长h=0.05，分别使用显式欧拉算法、隐式欧拉算法、Runge-Kutta算法求解式(1)的常微分方程，给定自变量x，求解值y，同时计算理论值，综合绘制出曲线图如图2所示。

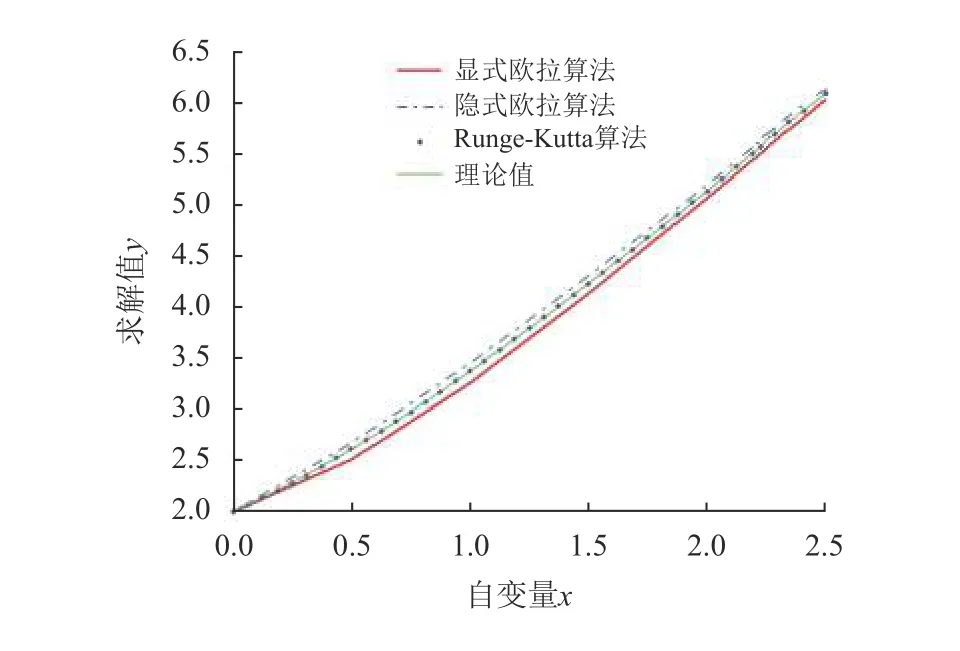
图 2 3种算法精度比较图Fig.2 Comparisons of three algorithms in precision

从图2中可以看出，Runge-Kutta算法求解结果几乎与理论曲线重合，它的精度最高，而显式欧拉算法精度相比Runge-Kutta算法和隐式欧拉算法最低，隐式欧拉算法居中。

根据以上的分析，可知Runge-Kutta算法、隐式欧拉算法都具有较好的稳定性，精度较显式欧拉算法高。但是它们共同的缺点是计算量较大，不适合实时性要求高的虚拟手术系统，所以大部分的虚拟手术都采用显式欧拉算法来求解质点弹簧模型，从而进行软组织形变的模拟。显式欧拉算法一般只是一阶收敛，精度不高，误差较大，为实现逼真的模拟效果，时间步长需要设置得很小，这会导致整个形变过程延长，并存在进退性冲击波[15-16]。

为了提高显式欧拉算法的计算精度，文献[16]提出了一种改进的欧拉算法来求解质点弹簧系统的速度与位移矢量，以提高求解精度及降低求解步长的影响。运用显式欧拉算法求解速度v，并直接使用v的结果，用隐式的方法求解位移x。表达式如式(2)所示。其中，m为质点质量，变量上标t表示本时刻该变量的值，t+h表示下一时刻该变量的值，f 为系统所受的力。

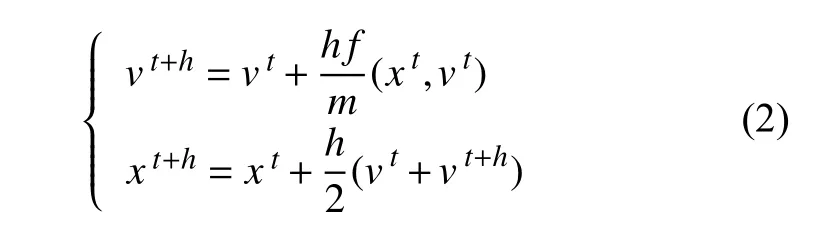
化简式(2)得位移表达式，如式(3)所示：

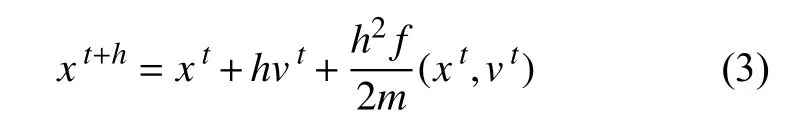
式(3)表明速度会影响系统所受的力f，从而影响位移x的求解精度。

这种算法相较于显式欧拉算法提高了计算精度和稳定性，但由于速度v采用显式欧拉算法求解，所以求解速度的精度还不够高，且受步长h的影响还比较大。

2 中点平均算法

2.1 算法基础

中点法常用于求解常微分方程，即应用于求解质点弹簧模型。采用本时刻 ft与下一时刻 ft+h之间的中间时刻t +h/2 处的 ft+h/2来求解速度vt+h。它所需的时间步长小于Runge-Kutta算法，精度比显式欧拉算法要高，但低于Runge-Kutta算法，具有较快的计算速度和较好的实时性。

平均法采用 vt和vt+h的平均值来求解 xt+h，表达式如式(4)所示。它的计算速度相比显式欧拉算法慢，但比Runge-Kutta算法要快，具有较好的计算精度和稳定性。

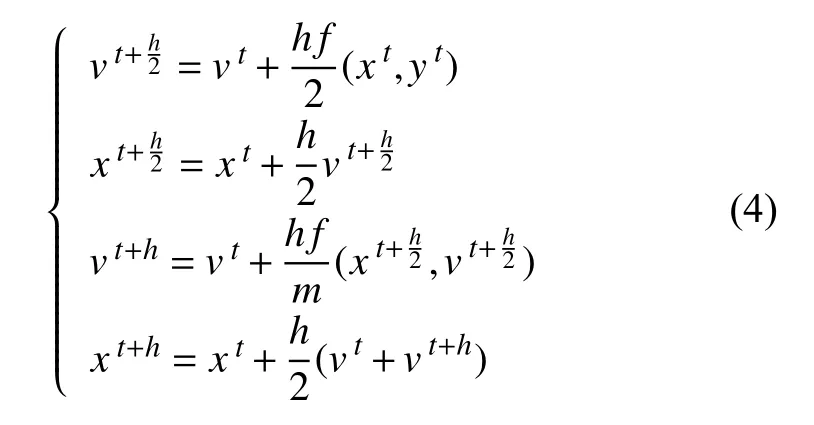
将式(4)中的vt+h代入位移x的表达式中，化简位移表达式，如式(5)所示：

基于这两种算法，同时考虑到形变的实时性和精度，本文提出一种改进的算法——中点平均算法，即算法融合中点法和平均法的特点，采用中点法对速度v进行迭代求解，位移x则采用平均法进行迭代求解。虽然减缓了计算速度，但能够综合两者的优势，减小误差及减小受步长的影响，提升求解的精度。算法流程如图3所示。

图 3 中点平均算法流程图Fig.3 Midpoint-averaging algorithm step flow chart

2.2 算法后处理

在算法基础上，对提出的中点平均算法进行后处理，并提出一个比重参数α。大致思想是：在采用中点平均算法求解质点弹簧模型前，对于求解速度v，以步长h=0.000 1的Runge-Kutta算法的求解结果作为基准，不断对式(6)所示的速度表达式进行求解并与基准比较，直到找到一个合适的α，最后用此中点平均算法求解虚拟口腔手术系统中的质点弹簧模型，方法流程如图4所示。

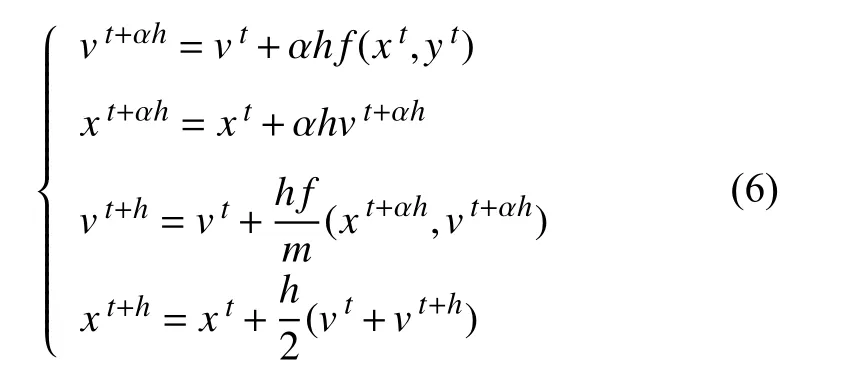
式(6)中α分别取值1/2，3/8，5/8，来验证α值的大小对求解精度有着不同程度的影响。

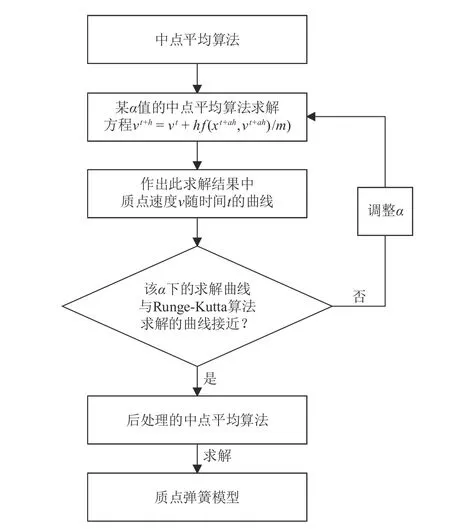
图 4 提升求解精度的方法流程图Fig.4 Method sketch for improving solution precision

以步长h=0.000 1的Runge-Kutta算法求解的速度为理论曲线。在算法的对比中，步长大小的选取会影响比较结果的直观程度。因此这里选取步长较大的2个值，h为0.1和0.4来求解质点运动状态。分别绘制出质点速度v的理论曲线和α=1/2，α=3/8，α=5/8时的求解速度v曲线，如图5的(a)、(b)所示。若某α下求解的速度v曲线与理论曲线更接近，则证明该α值调整的中点平均算法具有更高的求解精度。

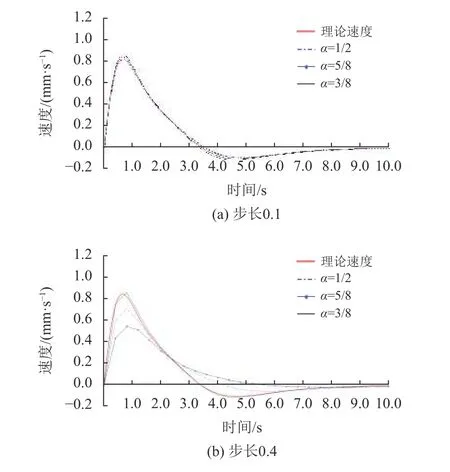
图 5 不同α对应的速度曲线Fig.5 Speed curves corresponding to different α

从图5结果中可看出，步长h=0.1，α=1/2时取得最好的求解精度；步长h=0.4，α=3/8时取得最好的求解精度。

因此，在原有算法基础上，在确定的步长下，可以通过求解一个适合的α来提升求解精度，并且不增加计算量。

在Unity3D中建立基于质点弹簧模型的虚拟牙龈软组织模型，并应用后处理的中点平均算法进行求解，图6为牙龈软组织切割前后的形变效果图。

图 6 牙龈软组织切割效果Fig.6 Cutting effect of gingival tissue

3 算法与欧拉算法的比较

中点平均算法与改进欧拉算法可通过式（5）和式（3）进行比较。改进欧拉算法采用t时刻的力ft计算下一时刻的位移 xt+h，而中点平均算法采用t+h/2 时刻的力 ft+h/2来 求解下一时刻的位移 xt+h，可知中点平均算法具有更高的计算精度，并且中点平均算法没有用到显式欧拉算法，使它对求解步长的影响不大。所以对于计算精度与受步长的影响，中点平均算法都具有更好的表现。

在MATLAB中，以步长h为0.000 1的Runge-Kutta算法求解的位移和作用力曲线作为理论值曲线，分别采用显式欧拉算法、改进欧拉算法及中点平均算法对质点进行状态求解，作出求解结果曲线。从而验证中点平均算法的求解精度优于显式欧拉算法和改进欧拉算法，对比如图7所示。

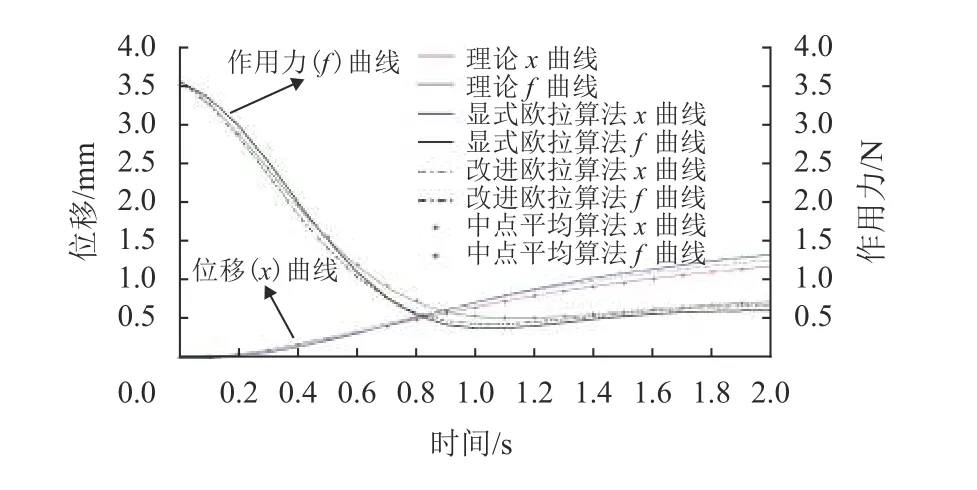
图 7 不同数值求解方法求解质点运动状态对比图Fig.7 Comparisons of particle motion state by different numerical solutions

从图7可知，中点平均算法具有较好的求解精度，几乎与理论线重合。改进欧拉算法相较显式欧拉算法有更高的求解精度，但没有中点平均算法高。

这里进一步探讨步长的选取分别对显式欧拉算法、改进欧拉算法以及中点平均算法的影响。在MATLAB中分别用这3种算法对不同步长h的质点运动状态进行求解。

在图8中绘制出显式欧拉算法、改进欧拉算法及中点平均算法求解的质点运动状态曲线图。

图 8 3种算法求解的质点运动状态Fig.8 Motion state of point solved by three algorithms

对比图8的(a)、(b)、(c)可以发现，显式欧拉算法受步长h的影响最大。改进欧拉算法受步长影响相对于显式欧拉算法更小，但由于其求解速度的时候采用的是显式欧拉算法，所以它受步长h影响依然较大。而中点平均算法采用中点法求解速度，然后再用平均法求解位移，这样就一定程度上减小了受步长的影响。从图8(c)可以看出，当h取0.02或h取0.1时，所求的结果几乎与理论结果重合；当步长h取0.4这样较大的值时，中点平均算法相比显式欧拉算法和改进欧拉算法依旧有更高的求解精度，这充分说明了中点平均算法能很好地满足虚拟口腔手术的实时性和真实性要求。

这里对虚拟口腔手术器械碰撞牙龈软组织进行模拟，在Unity3D中分别应用中点平均算法、显式欧拉算法和改进欧拉算法建立的质点弹簧模型模拟牙龈软组织的形变，图9为牙龈软组织碰撞前后的形变效果图。

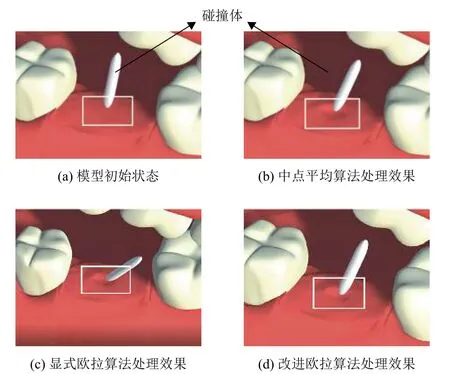
图 9 牙龈软组织碰撞效果Fig.9 Collision effect of gingival tissue

从图9可以看到，在相同的环境和作用力下，3种算法处理的软组织形变都满足虚拟口腔手术的真实性要求。中点平均算法处理的牙龈形变效果相较另外两种算法要更平滑，这也说明了中点平均算法相比具有更高的求解精度。

4 结论

本文提出了一种中点平均算法并对其进行后处理，使其对基于质点弹簧模型的牙龈软组织的求解精度在不增加计算量的前提下进一步提升。随后通过在MATLAB中分别采用显式欧拉算法、改进欧拉算法和中点平均算法这3种算法求解质点弹簧模型中质点的运动状态，验证了中点平均算法在三者中具有更高的求解精度，以及受时间步长的影响更小，满足虚拟口腔手术的实时性要求。在Unity3D中分别应用这3种算法对牙龈软组织模拟仿真，中点平均算法的形变效果也更为理想。尽管本文提出并进行处理的中点平均算法已展示其优越性，但算法尚需继续优化，使之得到更广泛的应用。