正弦开洞波纹钢板剪力墙抗侧性能研究

郭宗宏

（河北工程大学土木工程学院 河北邯郸 056038）

1 有限元模型的建立

1.1 模型设计

设计参数包括波纹钢板宽度和洞口宽度三个几何参数，模型设计如表1所示。

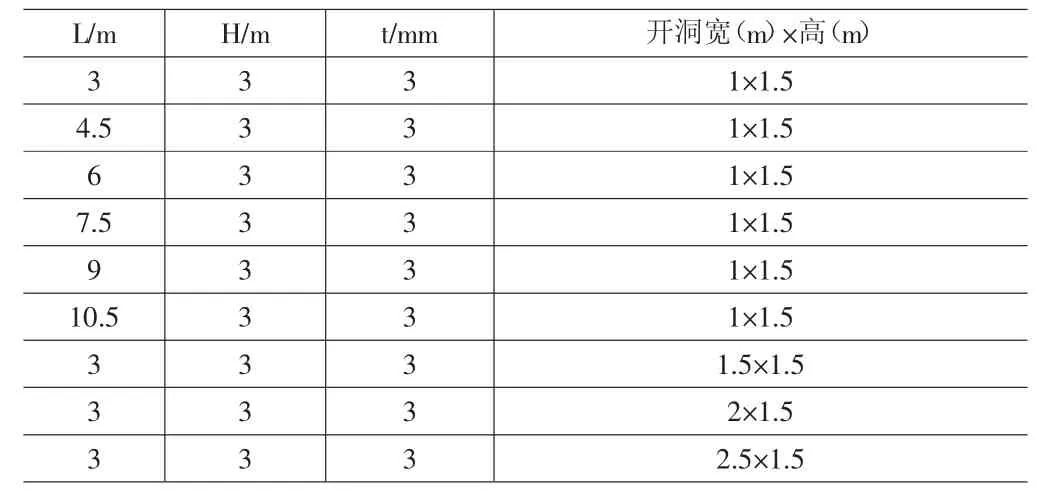
表1 参数分析取值

为了消除因框架尺寸不同而对正弦开洞波纹钢板的影响，本文只取一种尺寸框架结构，梁、柱均钢管尺寸为150mm×100mm×6mm。

1.2 材料模型和单元选取

波纹钢板和梁、柱的钢材屈服强度分别取235MPa和345MPa，钢材弹性模量Ey为206GPa，泊松比ν为0.3，密度为7850kg/m3，屈服强度fy为235MPa，强化阶段的弹性模量为E′=E/100，框架和正弦开洞波纹板采用4节点减缩积分壳单元（S4R）进行模拟分析。

1.3 边界条件

剪力墙为两个部分即框架和波纹钢板如图1所示[1-3]，框架和波纹钢板采用Tie连接，约束框架柱底部所有节点的3个平动自由度和x轴、z轴的2个转动自由度，限制框架梁的平面外自由度进行。取一阶屈曲模态的H/200倍做为剪力墙的初始缺陷[4]。

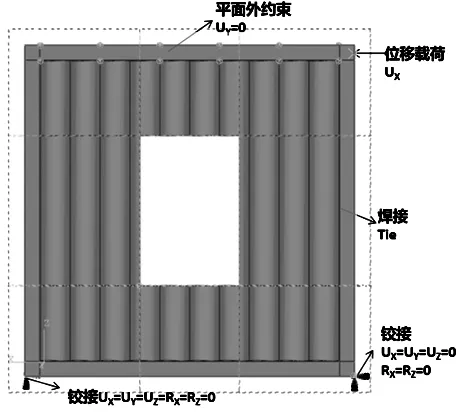
图1 正弦开洞波纹钢板剪力墙

2 有限元参数对正弦开洞波纹钢板剪力墙抗侧性能的影响分析

2.1 波纹钢板长度的影响分析

在其余参数不变的情况下，对比不同长度下剪力墙力学性能，如图2所示。

图2 波纹钢板长度的影响

波纹钢板的长度的改变对剪力墙的抗侧性能影响较大。长度每增长1.5m，其初始抗侧刚度分别增加了96.6%、54.7%、29.3%、22%、10.7%。剪力墙屈曲载荷分别增加了45.2%、34.4%、20.5%、18.9%、14.6%。剪力墙的峰值载荷分别增加了44%、30.8%、16.9%、19%、14.4%。随长度的增加，剪力墙的初始抗侧刚度、屈曲载荷和峰值载荷增长速率不断降低。

2.2 波纹钢板洞口宽度的影响分析

在其余参数不变的情况下，对比不同洞口宽度下剪力墙力学性能如图3所示。

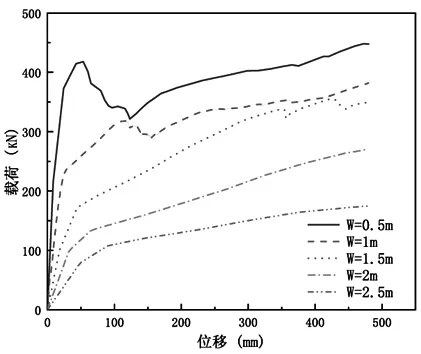
图3 波纹板洞口宽度的影响

波纹钢板洞口宽度的改变对剪力墙的抗侧性能影响较大。宽度每减小0.5m，其初始抗侧刚度分别增长了47.9%、45.2%、47.1%。屈曲载荷分别增长了55.4%、39.6%、34.2%。洞口宽度大于1.5m时，剪力墙没有明显的峰值载荷。

3 结论

波纹钢板长度的增长和洞口宽度的增宽都会对剪力墙的抗侧性能产生显著的影响，随着长度增长和洞口宽度减小其初始抗侧刚度、屈曲载荷和峰值载荷不断的增加，但其增长速率却在不断降低。