基于FLUENT三维数值模拟的溃坝洪水流动特性分析

王兴华，付成华，穆宵枭

(西华大学能源与动力工程学院，成都 610039)

2018年7月23日晚，老挝东南部桑片-桑南内水电站副坝发生溃坝；2019年1月25日，巴西东南部米纳斯吉拉斯州布鲁马迪纽市发生溃坝事故，均造成重大的生命财产损失及环境破坏。溃坝问题作为一种低频率、高危害的社会致灾因素[1]，越来越受到人们的关注，溃坝水流数值模型也被广泛研究。为了模拟溃坝水流，开发了大量的一维、二维模型[2]，这些模型适用于确定溃坝水流的淹没深度和到达时间，但由于对控制方程做了假设，例如静水压力分布、不明显的垂直加速度和自由表面曲率等[3]，不能准确地表现水流在空间上的演进变化规律，不适应于计算溃坝初期、溃坝波前和溃坝结构物附近水流，模拟这些复杂流动应基于使用雷诺平均N-S方程的三维模型。

基于雷诺平均N-S方程的三维溃坝模型，主要耦合紊流模型和自由界面捕获法，利用有限体积法求解控制方程。紊流模型主要有一方程模型、两方程模型(标准k-ε、RNGk-ε、Realizablek-ε、标准k-ω、SSTk-ω)和大涡模拟，其中标准k-ε模型在工程中应用最多，计算量适中，有较多的数据积累且相对精确。自由界面的捕获问题一直是三维模型的一个难点，目前主要有无网格法、移动网格法和固定网格法三类。如光滑粒子流体动力学法(SPH)[4]在不使用计算网格的情况下，用一组流体粒子代替流体运动，模拟自由表面运动；移动粒子半隐式法(MPS)[5, 6]，着眼于跟踪粒子的运动学和动力学性质变化过程，各粒子之间通过核函数相互联系；由Hirt和Nichols[7]提出的VOF法，通过跟踪计算网格中每个计算单元相对于其中一个流体相的体积分数来捕获界面位置，是研究多相流最常见的方法之一，已被大多数溃坝水流模型所采用。Stansby P K等[8]通过试验研究了高度不同的两立方水体的溃坝过程。Lauber和Hager[9]在平底矩形水槽中对溃坝洪水在下游无水情况下的演进规律进行研究，得出其水深和流速分布规律。王嘉松等[10]应用组合型TVD格式, 模拟了瞬间全溃溃坝波的传播、反射和绕射。肖潇等[11]对比分析了溃坝水流的模拟方法，结果表明利用FLUENT得出的计算结果更为准确，水位变化情况更加符合实际情况。王晓玲等[2]建立耦合VOF法与k-ε紊流模型的三维溃坝洪水演进数学模型，模拟了三维溃坝洪水在复杂淹没区域的演进。袁岳等[1]结合有限元法和有限体积法处理二维浅水方程，模拟了溃坝水流流经有障碍物的下游河道时的传播过程，得到各时间段的水位变化和水流演进情况。总的来说，三维数值模拟已逐渐成为现阶段研究溃坝水流的热门方法，但结合紊流模型和自由面追踪法系统地研究不同工况模型下水位变化规律和水流演进的还较少，同时由于实际溃坝问题具有很大的不确定性，利用数值模拟开展溃坝水流流动特性研究仍十分必要。

在前人研究的基础上，本文利用FLUENT软件建立溃坝三维数值计算模型，将下游有水的全溃坝、下游无水设障碍物的全溃坝、下游无水的局部溃坝3种工况整合到一起，采用VOF法对溃坝水流进行自由表面追踪，结合k-ε紊流模型模拟溃坝水流在演进过程中的水位变化情况以及负波对水流传播的影响。

1 基本方程和计算方法

1.1 基本方程

溃坝水流数值计算模型依据的基本方程有连续性方程和雷诺平均N-S方程。

连续性方程：

▽u=0

(1)

雷诺平均N-S方程：

(2)

式中：μeff=μ+μt；u为流速；t为时间；p为压力；ρ为密度；f为外力；μ为动力黏度；μt为湍流黏度，其中外力为重力，因此f=ρg，g为重力加速度。

上述方程采用保守形式，在含水区域内求解控制方程时，由于密度是连续且恒定的，因此密度不包含在动量方程的时间相关和对流项中。尽管与对流项相比，特别是在初始阶段，溃坝流中的扩散可以忽略不计，但为了保持雷诺平均N-S方程的一般形式仍然保留了扩散相，如式(2)所示。

k方程：

(3)

ε方程：

(4)

(5)

(6)

式中：xi，xj为坐标分量；Cu为经验常数，建议取值为0.09，σk=1，C1ε=1.44，C2ε=1.92，σε=1.3。

1.2 VOF法追踪自由表面

VOF法是根据每个时刻在网格单元中流体的体积变化来追踪自由表面，其基本思想是，对于每一个计算单元，都有一个特定的标量，表示给定单元的填充程度，例如水，如果在某个单元格中，该值为0，则为空；如果等于1，则充满水；如果该值介于1和0之间，则可以说该单元格在气液交界面，也就是说水的体积分数α被定义为一个单元中的水体积与给定单元的总体积之比。相应的，1-α表示给定单元中第二相的体积分数。在VOF法中，气液混合物的物理参数ρ、μ、μt可由体积分数作平均。

ρ=αρ1+(1-α)ρ2

(7)

μ=αμ1+(1-α)μ2

(8)

μt=αμt1+(1-α)μt2

(9)

这里的1和2分别表示液体和气体。流体体积分数α满足对流输运方程的解：

(10)

1.3 数值求解法

本模型数值求解采用PISO算法，该算法是SIMPLE的扩展，在每个迭代步中增加了动量修正和网格畸变修正过程，使得到的压强场更准确，计算收敛也越快。PISO算法包括一个预测和两个校正，其目的是利用预测校正更好地满足连续性方程和N-S方程。PISO算法步骤如下：

(1)预测：假设一个压力场p*，利用p*求解动量离散方程，得出相应的速度场u*、v*。

(2)校正1。对假设的压力场进行修正，求解压力修正方程得到p′，计算压力修正量、速度修正量为u′、v′，得到压力修正值和速度修正值p**、u**、v**。

p**=p*+p′

(11)

u**=u*+u′

(12)

v**=v*+v′

(13)

(3)校正2。

p***=p**+p″；p″=p*+p′

(14)

u***=u**+u″；u″=u*+u′

(15)

v***=v**+v″；v″=v*+v′

(16)

式中：p***、u***、v***分别为压力修正值和速度修正值；p″、u″、v″分别为压力修正量和速度修正量，设置p=p***，u=u***，v=v***，若修正后的压力场相对应的速度场能够满足连续性方程，则p、u、v为正确的压力速度分量，否则将令p*=p，u*=u，v*=v，重复步骤(1)直至满足条件。

2 溃坝洪水演进分析

2.1 下游有水的全溃坝

(1)网格模型。在长15.24 m、宽和高均为0.4 m的水库中，闸门位于下游9.76 m处，水库初始水深h0=0.1 m，下游水深为0.045 m，三维几何模型如图1所示，将空间尺度进行归一化处理，h/h0=0处为闸门位置，h为水位高度，重力加速度的方向与z轴相反。模型划分为六面体结构网格，数量约为224 700个。

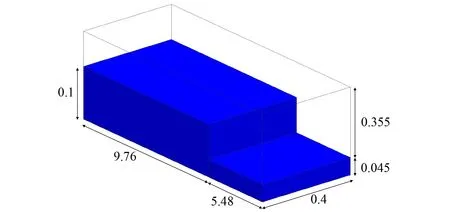
图1 三维模型图(单位：m)Fig.1 Three-dimensional model

(2)边界条件。由于模型整体偏细长，单精度求解器可能不能足够精确地表达各尺度方向的节点信息，因此本模型采用精确度更高的双精度求解器计算，残差值收敛标准为低于10-5。水库顶部设置成压力入口，出口边界设置为压力出口，出口位置压力参考为一标准大气压，回流设为0。水库底部和左右壁面设置为固壁边界，默认为是无滑移光滑壁面，采用壁面函数法。水库上游处水体在重力作用下流向下游，设为内部面边界，流体体积分数设为1。计入体积力，设置z方向重力加速度为-9.81 m/s2。下面两种模型边界条件设置相同。

(3)计算结果分析。对湿河床溃坝初期进行数值模拟计算，不同时间(t=0.22 s、t=0.32 s、t=0.52 s、t=0.76 s)水位高度计算值与实验值[12]比较结果如图2所示，图3和图4表示溃坝过程中不同时间(t=0.22 s、t=0.32 s、t=0.52 s、t=0.76 s)水面的变化。计算结果表明，闸门拉开瞬间，上下游交界处水面有明显的波动，且以波浪形式向下游演进，形成的第一个波浪波顶高度在演进过程中变化不大[13](如图3所示)，同时，t=32 s后由于负波的影响，上游水面出现波动，波动幅度随水流演进过程减小且并呈稳定趋势，闸门处水面也逐渐趋于平稳。

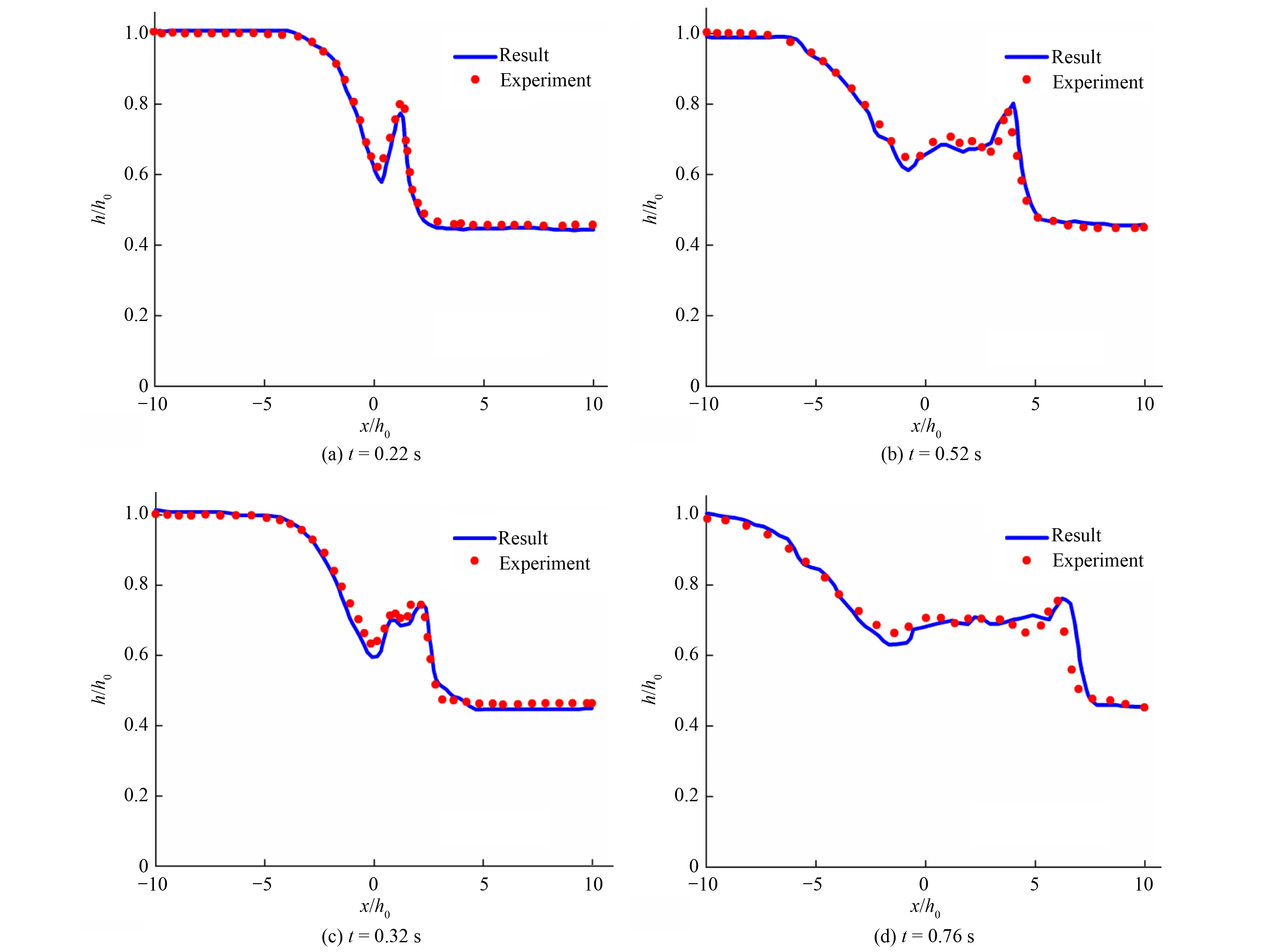
图2 不同时间水位高度变化模拟值与实验值对比Fig.2 Comparison of simulated and experimental values of water level height change at different time

图3 不同时间水位变化图Fig.3 Water level change chart at different time

图4 不同时间水面的二维变化Fig.4 Two-dimensional variations of water surface at different times

2.2 下游设障碍物的全溃坝

(1)网格模型。取一长9.03 m，宽0.3 m，高0.34 m的水库，闸门位于水库下游4.65 m处，水库初始水深h0=0.25 m，下游为干河床，考虑与实际情况的吻合，障碍物设置成梯形，下游距闸门1.53 m 处，三维几何模型如图5所示，梯形障碍物截面尺寸如图6所示。模型划分为六面体结构网格，数量约为20.71 万个。

(2)计算结果分析。不同时间下水位变化的数值模拟结果与实验值[14]的比较如图7所示。从图7可以看出，在t=1.9 s、t=2.8 s和t=6.68 s时，水面较为平滑，而在t=3.68 s和t=4.74 s时，水面出现小波浪，水面变得不稳定。图8和图9表示溃坝过程中不同时间(t=1.9 s、t=2.8 s、t=3.3 s、t=3.68 s、t=4.74 s、t=6.68 s)水面的二维、三维变化。t=0 s时，水库中的水体在重力作用下迅速流向下游，上游水位开始下降，下游水位随之上升，下游设置的梯形障碍物形成不规则地形，水流流经下游障碍物时，水面发生剧烈变化，图8可以看出，当溃坝波到达梯形障碍物时，水流形成水跃；在t=1.9 s时，水面完全覆盖了梯形障碍物，由于水流受障碍物的阻碍影响，梯形障碍物左侧水位开始上升；在t=2.8 s时，梯形障碍物左侧的水位上升到一定高度，一些撞击障碍物的水波向上游反向流动；t=3.3 s时，障碍物左侧上升的水位达到最大值，溃坝波破碎，产生的负波向上游传播；t=3.68 s、t=4.74 s、t=6.68 s的水面线也显示了负波向上游传播的情况。综上可知，在重力作用下，溃坝水流受下游障碍物的影响较大，产生的负波干扰了水流演进。

图5 三维模型图(单位：m)Fig.5 Three-dimensional model

图6 梯形障碍物截面尺寸(单位：m)Fig.6 Cross-sectional dimensions of trapezoidal obstacles

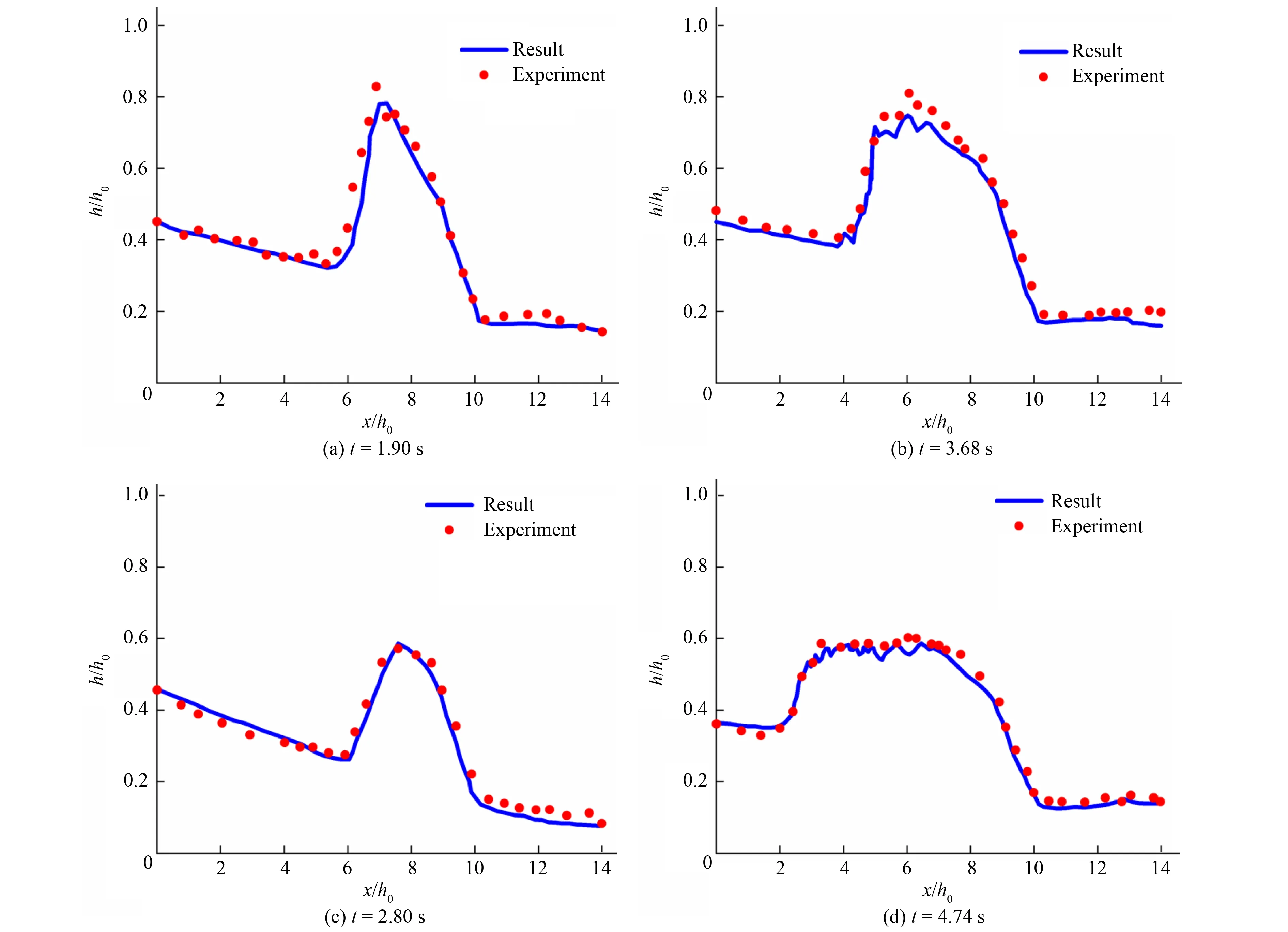
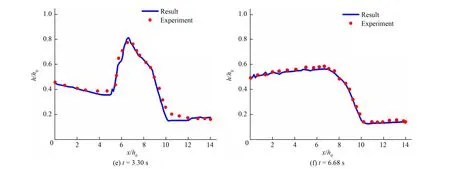
图7 不同时间水位高度变化模拟值与实验值对比Fig.7 Comparison of simulated and experimental values of water level height change at different time

图8 不同时间梯形障碍物水面的二维变化Fig.8 Two-dimensional variation of water surface of trapezoidal obstacle at different time

图9 不同时间梯形障碍物水面的三维变化Fig.9 Three-dimensional variation of trapezoidal obstacle surface at different time

2.3 下游无水的局部溃坝

(1)网格模型。为分析局部溃坝水流沿程的运动，取长为3 m,宽为2 m,高为0.7 m的水库，两个对称的不透水墙组成局部有孔的大坝，大坝位于水库下游1 m处，距左、右岸均为0.8 m,墙壁之间的距离为0.4 m,水库的初始水位为0.6 m，下游河床干燥，三维几何模型如图10所示。模型划分为六面体结构网格，数量约为48.16万个。

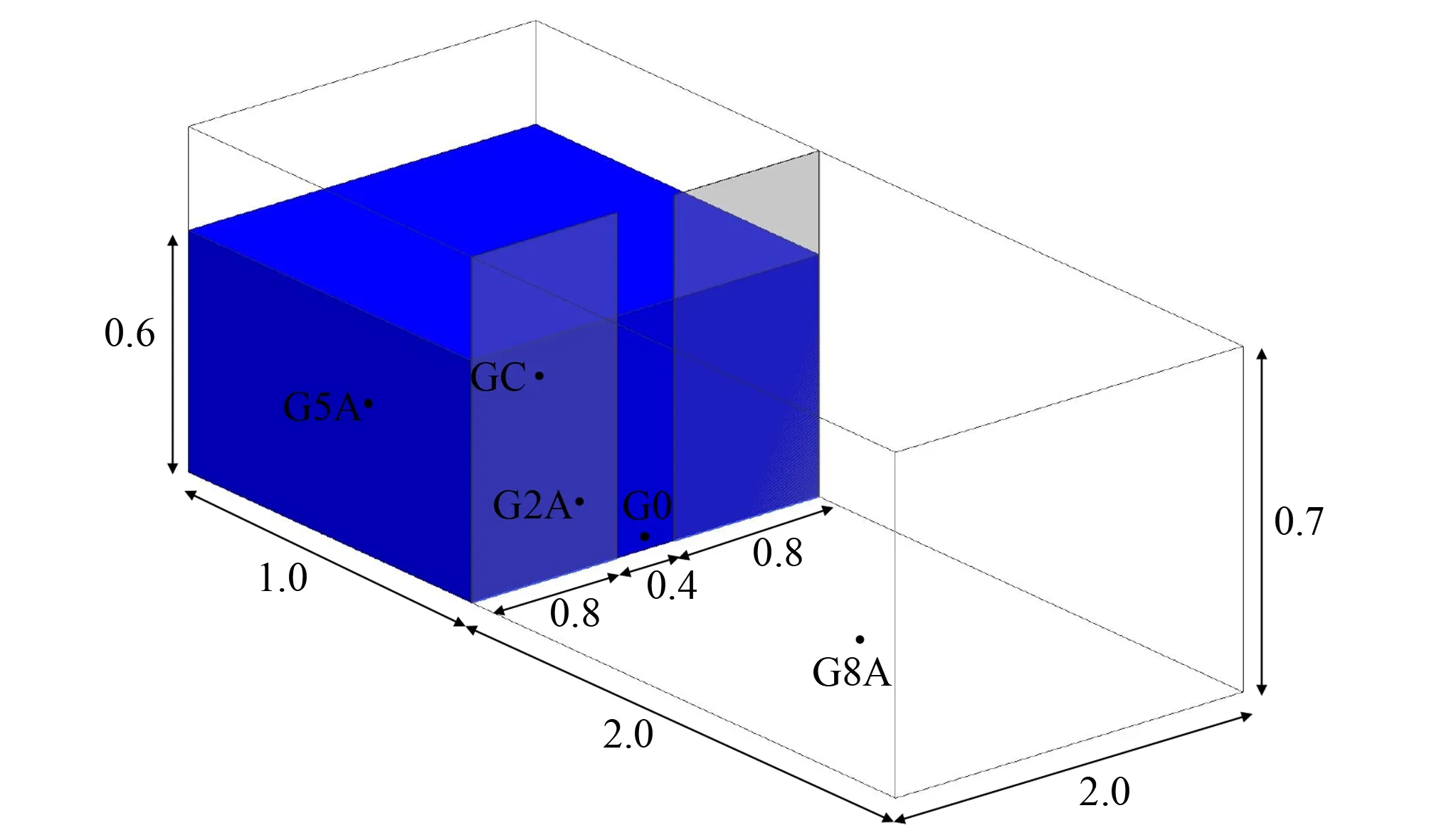
图10 模型三维图(单位：m)Fig.10 Three-dimensional view of the model

(2)计算结果分析。在水库上部、中部、溃口处与下游依次设置了G8A、GC、G5A、G0共4个监测点，监测点位置坐标见表1。4个监测点处水位随时间变化的数值模拟计算结果与实验值[15]的比较如图11所示。由计算结果可见，t=0 s时，溃坝开始，水库中的水体向下游运动，观测点G5A与GC两点处的水位随时间递减，随后大约在t=0.28 s溃坝水流到达监测点G8A，G8A处水位迅速升高后，随着时间的推移逐渐趋于平缓。大坝中心处的G0点水位呈现出一定的波动。由不同时间溃坝水流的二维和三维变化图12和图13可见，溃坝水流从溃口处流出后沿底部向两侧扩散，并逐渐填满下游区域。

表1 监测点位置坐标Tab.1 Position coordinates of monitoring points

图11 各监测点水位随时间变化模拟值与实验值对比Fig.11 Comparison of simulated and experimental values of water level changes with time at each monitoring point

图12 不同时间溃坝水流的二维变化Fig.12 Two-dimensional variation of dam-break flow at different times

图13 不同时间溃坝水流的三维变化Fig.13 Three-dimensional variation of dam-break flow at different times

3 结 论

采用FLUENT软件建立了三维溃坝水流模型，计算分析溃坝水流在下游的演进过程。考虑到实际溃坝问题中存在许多的不确定性，例如地形起伏、河床侵蚀、水土流失、溃坝过程中的渐进性等，分别考虑下游有水的全溃坝、下游无水设障碍物的全溃坝、下游无水的局部溃坝3种情况，用前人实验结果验证了数值模型的准确性。通过对溃坝水流演进过程和水位变化情况分析可得：

(1)下游有水时发生瞬间全溃，上下游交界处水面波动明显，而且出现的第一个波浪波顶高度最高，且在演进过程中高度变化不大。虽然受负波影响上游水面出现波动，但是随着水流演进波动幅度减小，水面趋于稳定。

(2)当下游为有障碍物的不规则地形时，溃坝水流撞击障碍物形成向上游的反射波，对水流演进有一定影响，同时受障碍物阻挡作用影响，障碍物左侧水位异常上升，而在实际情况中这种异常的水位上升可能会造成严重的环境破坏和经济财产损失。

(3)大坝发生局部破坏后，上游水位迅速下降，位于溃口处的水位逐渐降低且出现小幅波动，溃坝水流整体从底部向两侧扩散。

(4)溃坝水流受外界干扰条件的影响明显，实际水流行进过程中需尽量避免干扰，保证水流的平顺。

□