模型化强化学习研究综述*

赵婷婷，孔 乐，韩雅杰，任德华，陈亚瑞

天津科技大学 人工智能学院，天津300467

1 引言

深度强化学习（deep reinforcement learning，DRL）作为机器学习领域重要研究方向之一，是将深度学习的智能感知能力与强化学习的决策能力相结合，直接通过对高维感知输入的学习最终实现智能体的自主行为控制[1]，描述的是智能体为实现任务而连续作出决策控制的过程。DRL已经在无人驾驶[2-3]、智能交通系统[4]、机器人系统[5-6]、游戏[7]等领域取得了突破性进展，被认为是最有希望实现通用人工智能这个目标的研究领域之一。

深度强化学习具有一定的自主学习能力[8]，无需给定先验知识，只需与环境进行不断交互获得经验指数，最终找到适合当前状态的最优动作选择策略，取得整个决策过程的最大累积奖赏[9]，基本框架如图1 所示（因为深度强化学习与强化学习两者本质相同，本综述将交替使用深度强化学习与强化学习）。根据智能体所交互环境信息的利用方法，强化学习可分为无模型强化学习（model-free reinforcement learning）和模型化强化学习（model-based reinforcement learning）两大类[10]。

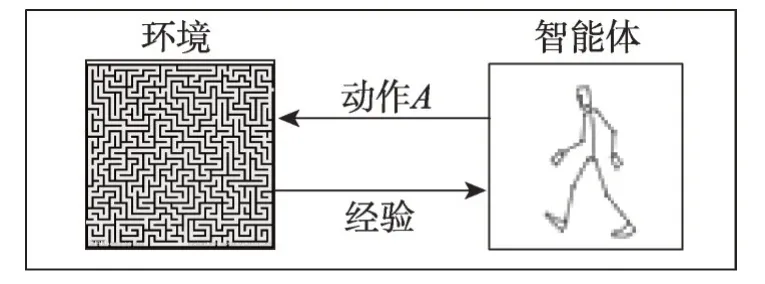
Fig.1 Framework of reinforcement learning图1 强化学习基本框架

无模型强化学习方法是智能体通过不断探索环境，不断试错，学习得到最优策略的方法[9]。为了达到预期的学习效果，无模型强化学习方法需要与环境进行大量的交互才能保证智能体的充分学习。无模型方法通常需要大量训练样本及训练时间，例如MuJoCo[11]根据任务的不同需要10 万以上的学习步数[12]；Deepmind 团队提出的学习酷跑的策略，需要64个GPU 学 习100 h 以 上[13]；DeepMind 提 出 的RainbowDQN 需要1 800 万帧Atari 游戏界面或大约83 h游戏视频对模型训练学习，而人类掌握游戏所用时间远远少于此算法[14]。然而，在实际物理场景中，收集充分的学习样本不仅需要花费大量时间与财力，甚至可能损坏智能系统。故而样本利用率及学习效率成为无模型强化学习在实际应用中的重要瓶颈问题。

模型化强化学习方法首先需要对环境建模，得到环境模型后，此类方法无需与真实环境交互，可直接利用学得的环境模型生成所需训练样本进行策略学习，从而在一定程度上缓解样本利用率低及学习效率低的问题。另外，如果所学得的环境模型足够精确，智能体就可根据该模型在其从未访问过的区域进行策略搜索。然而，学得的环境模型与真实环境间往往存在模型误差，难以保证算法的最优解渐近收敛[10]。因此，如何获得精准的环境模型是模型化强化学习领域的研究重点，这也是本文将要探讨的主要内容。

2 强化学习背景知识

2.1 马尔可夫决策过程

强化学习任务通常建模为马尔可夫决策过程（Markov decision process，MDP）描述(S,A,PT,PI,r,γ)[9]，其中S表示智能体的状态空间；A表示智能体的可选动作空间，状态S和动作A均可以是离散空间，也可以是连续空间，这取决于具体应用问题；PT(s′|s,a)表示当前状态st下执行动作at后，转移到下一状态st+1的状态转移概率密度函数；PI(s)表示选择初始状态s1的概率；r(st,at,st+1)表示当前状态st执行动作at后转移到下一状态st+1的瞬时奖赏；γ(0 ＜γ＜1)表示未来奖赏折扣因子。

如图2 是MDP 动态过程：首先，某智能体（agent）从初始状态概率分布p(s1)中随机选择状态s1后，依据当前策略π选择动作a1，然后智能体根据状态转移密度函数p(s2|s1,a1)从状态s1随机转移到s2，获得此次状态转移的瞬时奖赏r(s1,a1,s2)。此过程重复T次，可得到一条路径，T为时间步长。

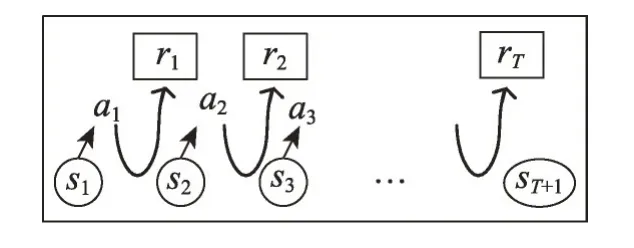
Fig.2 Markov decision process图2 马尔可夫决策过程

强化学习的目标是找到最优策略π*，从而最大化期望累积回报。

其中，累积期望回报表示为Jπ:=∫p(h)R(h)dh，p(h)=表示路径的概率密度函数，p(st+1|st,at)表示当前状态st执行动作at到达下一状态st+1的概率；累积回报，其中γ是折扣因子，通常0 ＜γ＜1，折扣因子γ决定了回报的时间尺度。

2.2 模型化强化学习和无模型强化学习

根据智能体与环境交互模式的不同，强化学习可分为模型化强化学习与无模型强化学习，二者的区别主要是智能体是否已知或需要计算环境动态模型，即状态转移密度函数P(st+1|st,at)[15-16]，如图3所示。

Fig.3 Two types of reinforcement learning图3 两种强化学习模式

无模型强化学习中，智能体直接与真实环境交互获得数据进行策略学习。此类方法不需要拟合环境模型，也不存在模型误差，因而实现简单，应用广泛；然而无模型强化学习方法学到的策略只针对特定问题，一次只能学习一项具体任务，当任务更换时需重新收集大量样本进行学习[17]；此外进行策略学习时，智能体需要训练学习大量样本才可能取得良好的性能表现，这会降低样本利用率[17]，造成资源浪费。重复使用样本（importance sampling）可以提高样本利用率，但样本重复使用技术需要提前设定学习样本的使用方式，若样本利用不当，会造成学习目标方差大、收敛慢的问题[15]。近年，随着硬件计算能力的提升，一定程度上弱化了样本利用率低的问题，但并没有从根本上解决样本利用率低的问题。

模型化强化学习方法首先利用智能体与环境交互获得的数据学习环境模型，然后收集所得模型产生的训练样本，最后使用强化学习算法优化动作选择策略，完成任务。整个过程不涉及提前设计样本使用模式的问题[18]。此外，相比无模型强化学习中智能体必须与真实环境交互才能得到其他未知状态值的情况，模型化强化学习中，环境模型一旦拟合，智能体就无需再与真实环境交互，可直接利用学到的模型预测未来状态，极大提高数据利用率。另外，环境模型通常包含外界环境模型与系统自身模型，如果能够得到一个精准的环境模型，便意味着智能体得到了一个较好的描述自身系统的模型，当外界环境变化时，系统自身的模型通常是不变的，因此只需要简单学习，环境模型便可适应新的外部环境，使智能体可以利用学到的模型快速进行推理。因此，模型化强化学习中学得的环境模型易于在不同任务及环境间进行迁移，具有较强的泛化能力[17,19]。

综上，如果环境模型能被准确建模，模型化强化学习将具有以上所述所有优势。然而，面对复杂的状态、动作空间，在有限可用样本的情况下，准确估计环境模型是极具挑战的。本文将以如何学习环境模型为核心内容，介绍并分析现有模型化强化学习方法。

3 模型化强化学习方法

Abbeel 等指出在确定性环境下，模型化强化学习无需精确的环境估计模型就可完成任务[20]。然而，实际应用中面临的环境往往是复杂的、动态的，因而对环境建模得到的状态转移模型与真实环境间存在模型误差，此时使用不准确的环境模型产生的数据进行策略学习还会产生更大的误差，从而带来双模误差。为减小模型误差，提高模型准确性，相关研究提出了很多解决办法，如Dyna模型化强化学习框架[21]、学习控制的概率推理方法[22]、基于最小二乘条件密度估计方法的模型化策略搜索算法[15]、嵌入控制方法[23]、基于神经网络动力学和无模型微调的模型化深度强化学习方法[24]、世界模型[25]等。本章将围绕上述相关研究进行讨论，分别从它们的主要思想、具体流程、方法优缺点进行详细综述。

3.1 Dyna 算法框架

Dyna 算法框架是将模型化强化学习和无模型强化学习结合，既从模型中学习，也从与环境交互的经历中学习，从而更新价值函数或策略函数的一类方法[21]。Dyna 算法框架并不是一个具体的强化学习算法，而是一类算法框架。

在Dyna 算法框架中，训练是在两个步骤之间迭代进行的：首先，使用当前策略，从与环境的交互中收集数据；然后，利用收集到的数据学习动态模型；其次，用所学的环境动态模型生成数据；最后，使用生成数据对策略进行更新。具体实现流程如算法1 所示。

算法1Dyna算法

输入：随机决策行为数据。

输出：算法得到的策略以及相应的奖励函数、状态转移模型。

步骤1初始化价值函数或策略函数，奖励模型r(st,at,st+1)和状态转移模型P(st+1|st,at)；

步骤2依据当前策略选择动作a，更新价值函数或策略函数，更新状态转移模型P(st+1|st,at)和奖励模型r(st,at,st+1)；

步骤2.1随机选择状态s和动作a，并依据状态转移模型P(st+1|st,at) 得到st+1，基于模型r(st,at,st+1)得到瞬时奖励r；

步骤2.2更新价值函数或策略函数。

算法1 中步骤2 可使用经典Q-Learning 系列的价值函数[26]、基于Actor-Critic 的策略函数[27]进行策略选择。基于Dyna 框架的模型化强化学习方法是该领域的主流方法，具体算法包括经典的学习控制的概率推理方法[22]及基于最小二乘条件密度估计方法的模型化策略参数探索方法[15]，下面详细介绍这两个算法。

3.1.1 学习控制的概率推理方法

模型化强化学习最大的问题是对环境建模时会产生模型误差。业界就如何减小模型误差，提高模型准确性展开了大量研究。学习控制的概率推理方法（probabilistic inference for learning control，PILCO）是该领域最经典的方法之一[15,28]，其主要思想是将环境中的状态转移模型建模为高斯过程（Gaussian process，GP）[29]，即以状态-动作对作为输入，输出是关于下一状态的概率分布。基于GP 的状态转移概率模型不仅可以捕捉到状态转移的不确定性，还将模型不确定性集成到了长期规划和决策中[30]。PILCO算法的具体流程如算法2 所示。

算法2PILCO 算法

输入：随机决策行为数据。

输出：算法得到的策略以及相应状态转移模型。

步骤1随机收集样本数据并初始化策略参数ρ；

步骤2使用收集的样本，通过无参数的GP 学习状态转移模型；

步骤3使用当前策略π与上述模型交互，通过确定性近似推理评估累积期望回报J(ρ)；

步骤4基于解析梯度的策略提升；

步骤5更新策略π，π*←π(ρ*)。

在随机收集样本后，通过无参数的GP 表示环境动态模型：

其中，st、at分别表示t时刻的状态和动作，μt+1=st+Ef[Δt]为均值，Σt=varf[Δt]为方差。

随后基于学到的环境动态模型将模型偏差纳入策略评估中，通过确定性近似推理评估累积期望回报J(ρ)：

其中，c(xt)表示人为指定的奖励函数，T表示路径长度。

最后通过可解析的策略梯度进行策略搜索并更新提升策略参数ρ。

PILCO 算法在机器人控制等复杂的实际问题中得到了广泛的应用[30]，也有相关研究针对PILCO 存在的问题提出了改进算法，如可实现多任务策略搜索的PILCO 算法[31]，以及面对复杂的高维度状态空间的深度PILCO 算法[32]。上述基于PILCO 的改进算法在不同方面改进了其性能，但此类方法假设条件状态转移概率密度函数为高斯分布，状态-动作联合概率密度函数为高斯分布，且奖赏函数须为指定的指数形式以保证策略估计及策略梯度能够解析地计算，这极大程度地限制了PILCO 算法在实际问题中的应用。

3.1.2 基于最小二乘条件密度估计方法的模型化策略搜索算法

针对PILCO 算法存在的根本问题，Tangkaratt 等提出了基于最小二乘条件密度估计的模型化策略搜索算法（model-based policy gradients with parameterbased exploration by least-squares conditional density estimation，Mb-PGPE-LSCDE）[15]。该算法首先使用最小二乘条件密度估计方法（least-squares conditional density estimation，LSCDE）[18]学习状态转移模型，再利用基于参数探索的策略梯度算法（policy gradient with parameter-based exploration，PGPE）[33]进行策略学习。学习流程如算法3 所示。

算法3基于最小二乘条件密度估计的模型化策略搜索算法

输入：随机决策行为数据。

输出：算法得到的策略以及相应状态转移模型。

步骤1智能体与环境交互，随机收集转移样本；

步骤2利用收集的样本对环境建模得到状态转移模型；

步骤3初始化当前策略π和策略参数ρ；

步骤4将学到的状态转移模型和当前策略交替使用，生成足够的样本序列。

智能体首先与环境交互进行随机采样，并使用采样得到的样本，通过LSCDE 方法对环境建模得到：

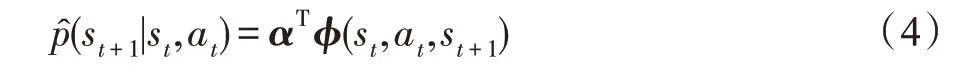
其中，φ(st,at,st+1)是基向量，α是M维参数向量，最小化下列平方误差就可得到最优参数α。

在得到稳定状态转移模型后，将该模型与当前策略交替使用生成足够的样本序列，并使用PGPE 方法进行策略搜索，更新策略参数：

式中，ε＞0 表示学习率，J(ρ)表示含参累积期望回报。

LSCDE 是一种非参拟合方法，相对比基于GP 的模型化方法，其最大的优势在于能拟合任意条件概率密度函数。此外，利用LSCDE 算法学到的状态转移模型易于生成样本；能够直接处理多维度的输入-输出问题[15]；对异常值很鲁棒；可以通过求解线性方程得到解析解；能够以非参最优速率收敛到真实条件概率密度函数[18]。基于LSCDE 的模型化策略搜索方法在采样预算有限的情况下具有很好的性能，极大提高了样本利用率，但难以处理高维度问题。

3.2 基于神经网络动力学和无模型微调的模型化深度强化学习方法

目前，神经网络已在众领域取得巨大成功[34]，与此同时研究者也在探索利用神经网络解决模型化强化学习中复杂、高维任务的方法[19]。其中，Nagabandi等人提出基于神经网络动力学和无模型微调的模型化深度强化学习方法（neural network dynamics for model-based deep reinforcement learning with modelfree fine-tuning，MBMF）[24]，该算法只需收集机器人与环境几分钟的交互数据就可找到最优策略，完成任务。

MBMF 方法将神经网络和模型预测控制方法（model predictive control，MPC）[35]结合，利用神经网络捕捉学习有效步态的动力学模型，所得模型可用于不同的轨迹跟踪任务，还可以用所得模型生成样本初始化智能体，使用无模型强化学习对初始步态微调，获得高任务奖励。

算法4MBMF 方法

输入：随机决策行为数据。

输出：算法得到的策略以及神经网络动力学模型。

步骤1建立神经网络动力学模型f，拟合状态变化与当前状态和动作的非线性关系；

步骤2使用梯度下降方法更新模型f；

步骤3定义模型化的控制器（controller）预测动作序列A(H)；

步骤4选择对应于最高累积奖赏的序列A*，执行动作序列中的第一个动作；

步骤5重复步骤3、步骤4 直到序列最终状态，并更新神经网络动力学模型（步骤2）。

算法4 表示的是仅使用模型化强化学习方法（model-based，MB）的学习过程。具体过程如下：

首先，建立神经网络动力学模型（状态转移模型）：

其中，st、at分别为t时刻智能体的状态和采取的动作，st+1表示t+1 时刻智能体状态，fθ(st,at)表示参数为θ的神经网络动力学模型，用于捕捉在执行某动作a的相邻状态间的变化。

其次，更新模型参数θ，损失函数为：

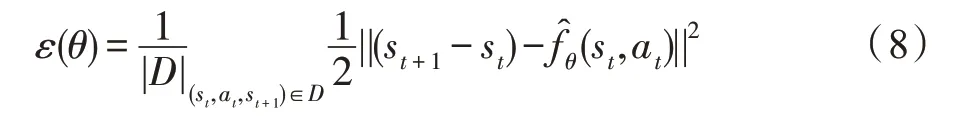
然后，使用任务奖赏函数和习得的动力学模型建立的模型化的控制器预测动作序列A(H)：其中，每个时间步t均随机生成K个动作候选序列,H为序列长度。

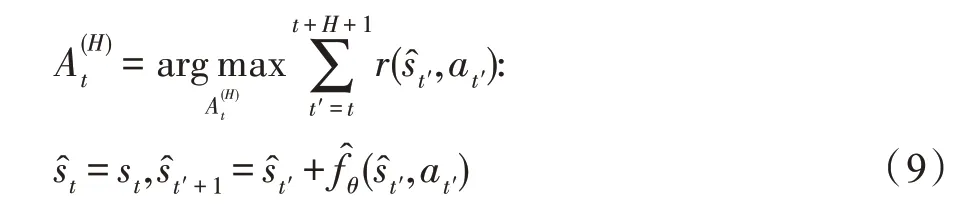
尽管强化学习中模型化方法比无模型方法学习特定任务的策略时更具样本效率和灵活性，但若存在模型偏差，其性能通常比无模型强化学习方法差。因此文章结合两者优势，又提出了一种简单且高效的MBMF 方法[24]。具体地，首先使用上述模型化方法中的控制器生成样本序列作为“专家知识”初始化无模型强化学习方法的策略参数，然后使用无模型方法——信任区域策略优化（trust region policy optimization，TRPO）[36]方法微调策略参数进行策略搜索。

3.3 嵌入控制方法

嵌入控制方法（embed to control:a locally linear latent dynamics model for control from raw images，E2C）是一种面向高维图像流的随机最优控制（stochastic optimal control，SOC）系统[23]。为解决原始图像作为输入带来的维度过高问题，E2C 方法将高维非线性系统的最优控制问题转化为低维隐空间中的局部线性问题，使得最优控制能够快速、简便地进行。

如图4 所示[23]，E2C 模型将高维、非线性的原始像素图像st作为系统输入，经变分自编码器（variational autoencoder，VAE）[37]的编码器（encoder）部分，将系统输入映射到低维隐空间中，随后在隐空间中将动态环境约束为局部线性模型，并计算KL 散度（Kullback-Leibler divergence）[38]进行模型更新。在模型稳定收敛后，E2C 模型可直接根据当前状态st和动作at，预测下一状态st+1。

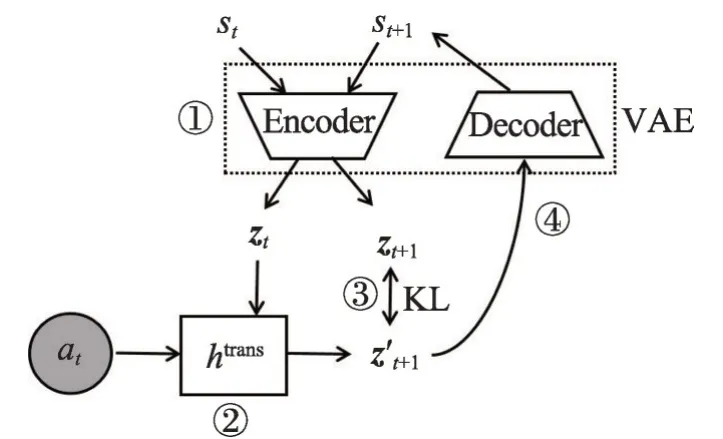
Fig.4 Information flow in E2C model图4 E2C 方法信息流

算法5E2C 方法

输入：随机决策行为数据。

输出：算法得到的策略以及相应状态转移模型。

步骤1利用VAE 将收集到的当前状态st映射到隐空间，得到隐状态zt；

步骤2在当前隐空间根据隐状态zt建立线性状态转移模型htrans；

步骤3对所得状态转移模型htrans更新训练，直至收敛；

步骤4将SOC 和状态转移模型htrans联合使用，获得最优控制。

算法5 为E2C 模型化强化学习方法具体流程。由于原始图像是高维的，很难直接处理，因此文章提出首先通过变分自编码器将高维图像输入数据st映射为低维隐空间中的zt：

其中，zt是st的低维隐表征，m是高维图像st到低维向量zt的映射函数，ω为系统噪声。

为得到局部线性模型的概率生成模型，此方法直接在隐表征z中令潜在表征线性化：

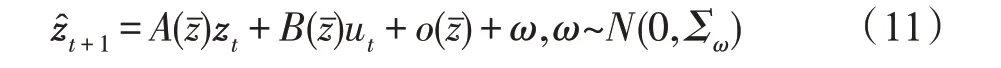
其中：

其中，htrans(zt)表示参数是ψ输入是zt的三层神经网络，vec表示向量化，WA、WB、Wo表示权重矩阵，bA、bB、bo表示偏差矩阵。

随后训练更新模型：利用得到的隐空间状态转移模型htrans和当前隐状态zt以及当前动作at预测隐空间中的下一状态；并使用上述VAE 对下一状态st+1编码得到zt+1，求与zt+1′间的KL 散度，微调线性状态转移模型htrans。

在模型稳定收敛后，将SOC 和状态转移模型htrans联合使用，获得最优控制。

E2C 方法不仅支持图像序列的长期预测，而且在解决复杂控制的相关任务有很大优势。与E2C 方法思想相比，Assael 所提出的基于深度动态卷积网络的策略学习方法[39]同样使用VAE 从图像中提取控制的隐空间表示，并在此基础上学习非线性模型。不同的是后者使用PCA（principal components analysis）进行预处理[40]，然而预处理后的数据在隐空间中不能保证长期预测不发散，也不能保证数据的线性，最终实验结果并不理想。

然而当系统动力学中存在噪声时，用于嵌入的编码器通常具有较大的近似误差，鲁棒的局部线性可控嵌入方法（robust locally-linear controllable embedding，RCE）[41]提出嵌入后验的变分近似方法，最终使得RCE 方法性能优于E2C 模型。

3.4 世界模型

世界模型（world models）是为通用强化学习环境所构建的神经网络生成模型，它可以在无监督的情况下快速学习到低维隐空间下的环境状态表示，甚至能够将智能体在学得的世界模型中训练，并将其策略迁移至真实环境[25]。世界模型框架如图5所示[25]，模型包含三个主要部分：将原始观测图像映射到低维隐空间中的视觉组件（V）；用于在低维潜在空间对未来状态的预测的记忆组件部分（M）；基于视觉组件和记忆组件的输出决定智能体所采取动作的控制组件（C）。

Fig.5 Flow diagram of world models图5 世界模型数据流

t时刻，智能体首先与真实环境交互观测得到高维原始图像，在V 部分利用VAE 得到原始图像的潜在编码zt，因此此部分的主要任务是状态的抽象、低维表示。随后在M 部分根据当前状态的潜在编码zt和采取动作at，使用基于混合密度网络的递归型神经网络（mixture density network combined with a recurrent neural networks，MDN-RNN）[42]预测下一状态的潜在编码zt+1，其中RNN（recurrent neural networks）[43]学习潜在空间的状态转移概率密度函数p(zt+1|at,zt,ht)，ht表示RNN 的隐藏状态。在智能体与环境的交互过程中，C 部分实现当前状态的潜在编码zt和系统自身的隐藏状态ht到动作的映射：

其中，Wc和bc分别表示权重矩阵和偏差向量。

算法6 的训练过程中，将大规模神经网络置于V部分和M 部分，利用无监督的学习方式分开训练学习智能体的环境模型；将C 模型设计为一个小型神经网络，使用协方差矩阵自适应进化策略（covariance matrix adaptation evolution strategy，CMA-ES）最大化累积奖励，对控制器进行优化[44]。

算法6世界模型方法

输入：随机决策行为数据。

输出：算法得到的策略以及状态转移模型。

步骤1随机收集数据；

步骤2训练VAE(V)部分，将原始输入映射到维度较小的隐空间中；

步骤3训练MDN-RNN（M）部分，得到转移模型P(zt+1|at,zt,ht)；

步骤4训练C选取下一步的行动，at=Wc[zt,ht]+bc；

步骤5使用协方差自适应调整的进化策略（CMAES）最大化奖赏，更新参数Wc、bc。

世界模型摒弃了传统深度强化学习的端到端的学习方式，采用对各个组件分开训练的模式进行学习，从而极大地加快学习速率。它针对不同任务能够取得较好结果，且易于复现，方法整体性能稳定。但使用VAE 作为V 模型压缩空间维度并将其训练为独立模型有其局限性，这是由于编码器可能编码与任务无关的部分观测结果。另外，受限于硬件存储能力，难以存储所有数据信息，会产生诸如灾难性遗忘之类的问题。

4 总结及展望

深度强化学习通过端到端的学习方式实现从输入到输出的直接控制，使强化学习能够扩展到以前难以处理的具有高维状态和动作空间的决策问题。它为整个社会实现真正智能化提供了有力的技术支撑，在机器人控制、游戏、自然语言处理、自动驾驶等领域取得了令人瞩目的成就，成为当前备受关注的研究领域。深度强化学习的成功依赖于大量的数据样本、计算资源及良好的学习算法，而获得大量的学习样本恰恰是DRL 在实际应用中的瓶颈问题。鉴于模型化强化学习在样本利用率方面的优势，本文对其展开了详细的综述、分析及展望。

对模型化强化学习而言，其核心的问题是如何提高环境模型预测的准确率。近年，生成模型，如变分自编码器[37]及对抗生成网络[45]，在数据生成方面取得了令人瞩目的成果，如何将成熟的概率生成模型更好地应用到模型化强化学习领域，进行精准的环境状态转移的预测是重要的研究方向。深度强化学习往往面对的是高维度、复杂的状态空间，针对此应用场景，样本利用率及维度灾难问题是该领域在实际中的瓶颈问题[15]。因此，如何在高维状态空间的低维表示空间预测状态转移模型是模型化强化学习能在实际中得以广泛应用的重要探索方向[25]。此外，现有深度强化学习方法面对给定的任务可以在训练环境中表现极好，但是往往不能泛化至环境中看似微小的变化，因此如何学习能够自适应的环境模型是模型化强化学习在实现通用人工智能过程中的重要课题。影响状态转移的因素包括智能体对于自身行动所引发的环境变化的内部隐状态的变化及外部环境的变化，智能体在学习环境的状态转移函数时，应该同时学习自身系统的内部隐状态变化[25]，从而在面对新环境时，能更快、更有效地将所学的环境模型适应到新的环境中。

模型化强化学习算法和无模型强化学习算法各有优缺点，将两种算法联合使用可以综合两者的优点，这将成为未来深度强化学习发展的热点，从而让深度强化学习算法更实用。未来工作的一个重要方向是将模型化方法和无模型方法更紧密、更高效地集成在一起，以便进一步提高样本效率，学习最优策略。另外，模型化强化学习与控制理论联系紧密，未来二者可互相借鉴成果，互相促进共同发展。