水下微穿孔板声超材料的几何结构优化∗

朱伟杰 崔汉国 何世平

（1.海军工程大学动力工程学院 武汉 430033）（2.湖北工业大学机械工程学院 武汉 430068）

1 引言

声呐罩的透声窗材料应具有高的强度和刚度，同时还应具有良好的透声性能［1］，目前声呐的主流建造材料是玻璃钢，玻璃钢虽然具有良好的透声性能，但是在高航速下由于玻璃钢模量比合金低得多，将产生很大的流激噪声，声呐的工作将受到很大的影响［2～3］。

当声波入射到非均匀结构的介质时，在声波的传播过程中，声场通常表现为非均匀的分布。但是对于具有亚波长结构的声学超材料，声波的波长远大于结构的多个周期，声波在该结构中传播时，相邻几个周期的运动趋于一致，表现出明显的长波特性［4］。通过在亚波长物理尺度上进行微结构的有序设计，得到的由多种弹性材料周期性排列组合而成的声学超材料，能够表现出自然界材料所没有的特殊性能，如负折射［5］、声隐形［6～7］、超透镜［8］以及超透射［9～10］等等。已有文献表明一定穿孔率的钢板无论多厚都具有良好的透声性能［11］。本文主要通过有限元分析比较微穿孔几何结构的改变对微穿孔板声超材料透声性能的影响，并对微穿孔的几何结构进行优化以达到最优的透声性能。

2 微穿孔板模型的建立及有效性验证

在有限元软件中，分析置于海水中的微穿孔板的声学性能，微穿孔中的介质为空气，平面声波从水介质中垂直入射到钢板中，运用压力声学和固体力学模块对三维模型进行仿真运算，如图1所示。

图1 浸泡在水中的微穿孔板示意图

2.1 模型的几何参数及材料参数

图2（a）展示的是微穿孔板XY平面的视图，其中虚线框内为一个周期单位，p为周期长度，r为微穿孔的半径。图2（b）展示是YZ平面的视图，h为钢板厚度，波数k=ω/c。

图2 微穿孔板几何参数

该模型中使用的水介质和空气介质的参数设定如下：水的密度ρw=1.0×103kg/m3，水中声速cw=1.49km/s，空气密度ρa=1.29km/m3，空气中声速ca=0.34km/s。钢板材料的基本属性：密度ρs=7.67×103kg/m3，杨氏模量E=2.05×1011Pa，泊松比nu=0.28，纵波声速csp=6 010m/s橫波声速css=3230m/s。

2.2 模型中边界条件的设定及网格划分

取图2（a）的虚线框中周期单位建立模型，微穿孔板浸没在海水中，如图3（a）所示。在水域中取微穿孔板两侧的两个面，分别设为声波入射面和出射面。在微穿孔板左侧的水域中设置背景压力场，背景压力场的类型设为平面波，压力幅值p0=1Pa，相位为 0rad，声波方向为｛X，Y，Z｝=｛sinθ，0，cosθ｝，平面声波从微穿孔板的左侧入射，在整个模型中传播。水域两端的两个平面的边界条件设为平面波辐射，声波遇到这两平面将完全辐射出去，不产生反射，将两侧的边界分别设定为Floquet周期边界条件，如图3（b）所示。最大单元网格大小设定为，其中λmin为声波在空气中的最小波长，网格划分如图3（c）所示。

该模型中微穿孔板的透声系数表达为［12］

其中ps为散射压力场。

图3 边界条件的设定及网格划分

2.3 模型有效性的验证

该微穿孔板的结构尺寸远小于声波波长，基于声学超材料等效介质理论，在假设钢板为完全刚性的条件下，其透声系数可表达为［13］

其中u与波长和微穿孔的厚度相关，λa为平面声波中空气介质中的波长，Zr为水的声特性阻抗和微穿孔板的等效声特性阻抗之比Zr=Zw/Ze，其中Zw=ρwcw/cosθ，Ze=ρaca/f，钢板的空隙率。

在相同的钢板厚度h=10mm和周期长度p=250μm的条件下，分别取孔隙率f=0.002、f=0.001、f=0.0005，得到不同孔隙率下的透声系数，如图4所示。

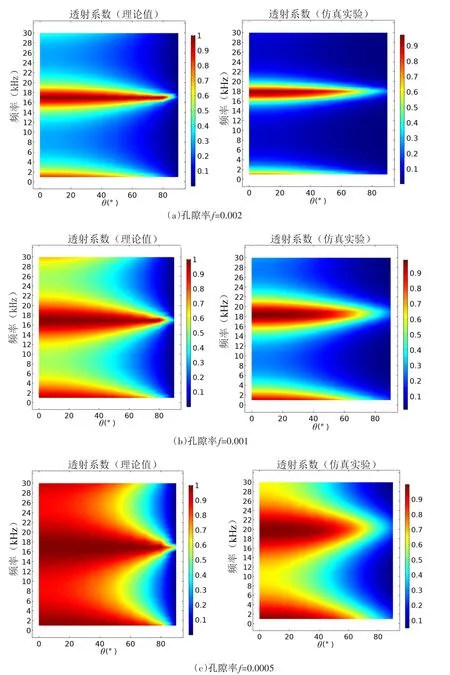
图4 钢板厚度h=10 mm时，不同孔隙率下微穿孔板的透声系数

由图4可以看出，有限元模型运算得到的透声系数总体上稍微小于解析理论值，误差主要来源于等效阻抗理论是在假设钢板为完全刚性的条件下进行的；但是变化趋势是一致的，可以认为该模型有效。

3 微穿孔板几何结构的优化

微穿孔的形状和排列方式是比较有限的，可通过建立不同的几何结构模型，分别比较不同微穿孔形状和排列方式对微穿孔板透声性能的影响。从中选取透声性能最优的微穿孔形状和排列方式，并采用遗传算法对微穿孔的孔隙率和板厚度进行进一步的优化。鉴于水下透声材料的透声性能检测主要是在声波垂直入射的条件下进行的，为了减少运算量、避免占用过多的计算机内存，下面只分析声波垂直入射的情况。

3.1 微穿孔形状对透声性能的影响

为了比较微穿孔形状对微穿孔板透声性能的影响，在上面模型的基础上保持周期长度p=250μm，取微穿孔板厚度h=5mm，孔隙率f=0.0003，更改微穿孔形状，比较正方形孔、正六角形孔和圆形孔对透声性能的影响。由图5，不同微穿孔形状的微穿孔板透声系数曲线几乎重合，可认为微穿孔形状对微穿孔板透声性能的影响很小。

图5 不同微穿孔形状对透声性能的影响

3.2 微穿孔排列方式对透声性能的影响

常见的排列方式有四方排列（如图2的模型）和三角排列（如图6所示）。由上面的分析可知微穿孔形状对微穿孔板的透声性能影响很小，鉴于圆形微孔的加工较其他孔的加工简单，下面选取圆形孔微穿孔板为研究对象。保持其他条件不变，建立圆形微穿孔三角排列的微穿孔板模型，分析其透声性能，和四方分布的圆形微穿孔模型作比较。由图7可知，在声波频率小于18300Hz时，四方排列的微穿孔板透声性能略比三角排列的微穿孔板差，在声波频率大于18300Hz时，四方排列的微穿孔板的透声性能比三角排列的微穿孔板有小幅度提升。总体可判断四方排列的微穿孔板透声性能略优于三角排列的。

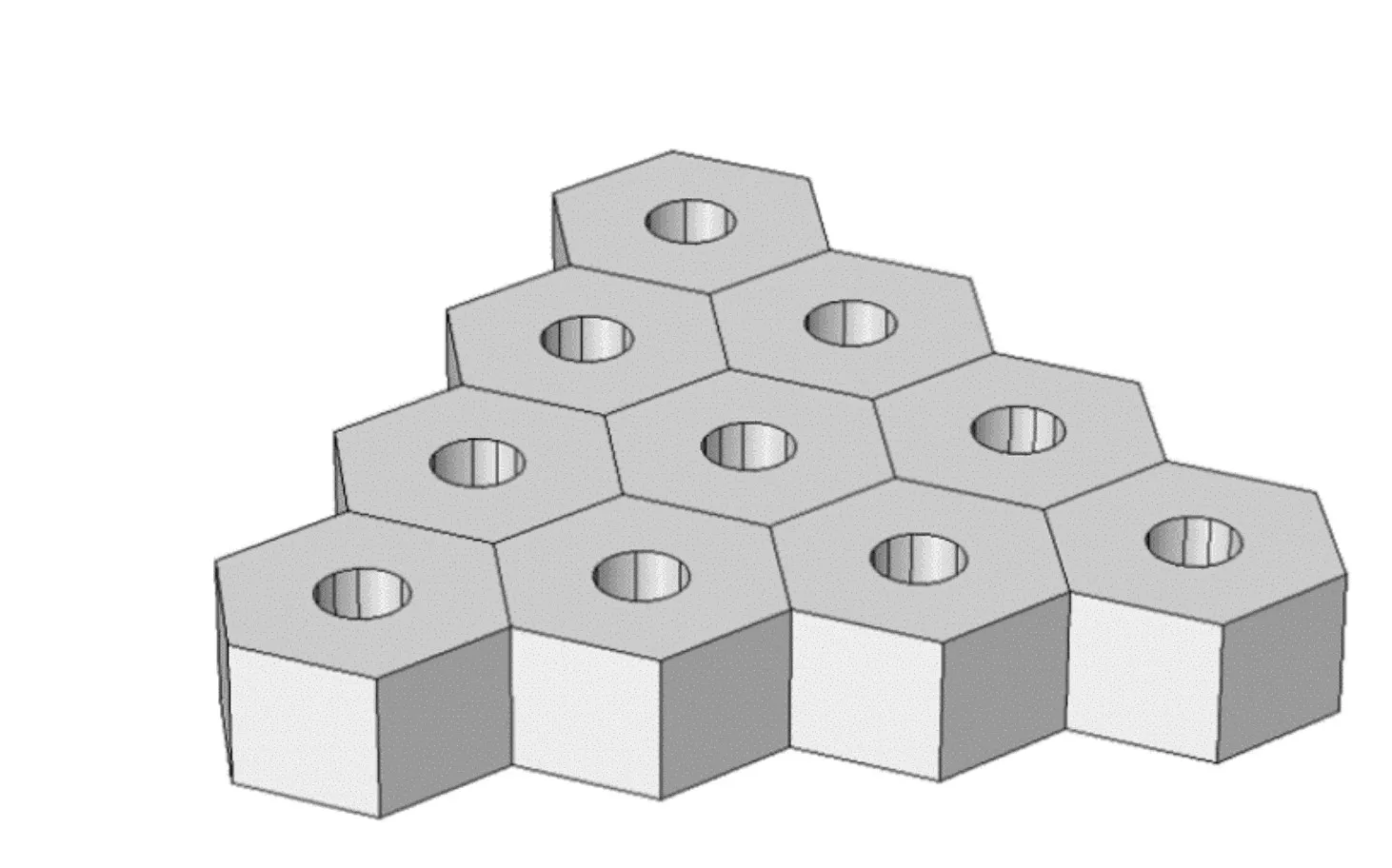
图6 微穿孔三角排列示意图

3.3 基于遗传算法对四方排列的圆形微穿孔板的几何尺寸优化

由前面的分析可知，微穿孔的形状对微穿孔板透声性能的影响几乎可以忽略不计，四方排列的微穿孔板透声性能要优于三角排列的。选取四方排列的圆形微穿孔板，采用具有全局搜索优化功能的遗传算法对微穿孔板孔隙率和板厚度进行进一步地优化。

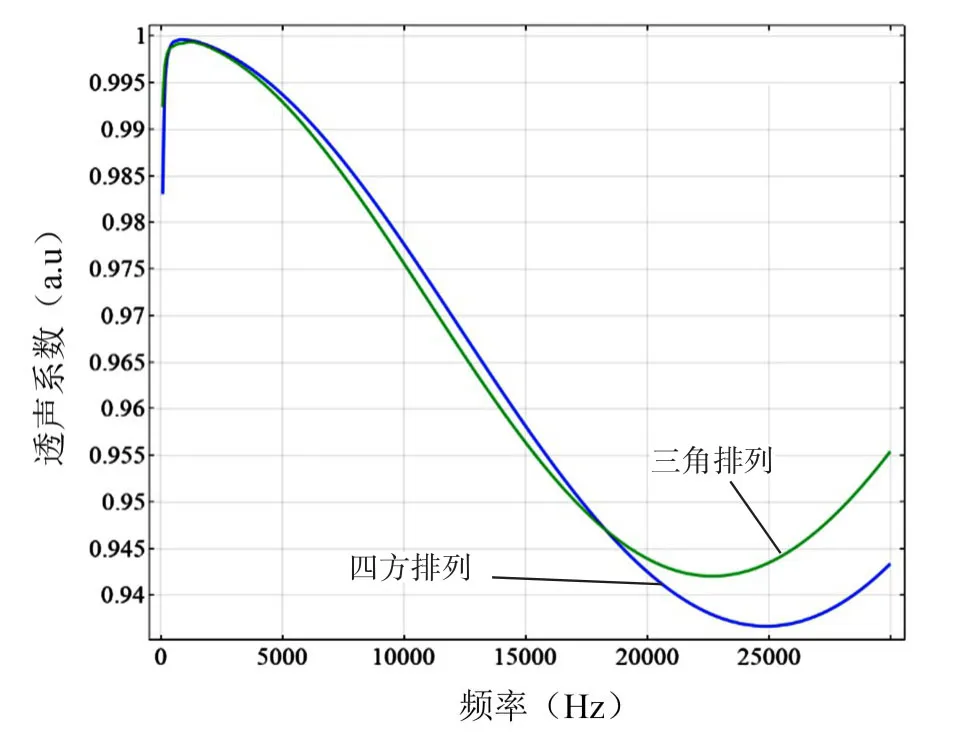
图7 不同微穿孔排列对透声性能的影响

定义适应度函数为“透声系数t”的平均值的相反数，定义变量孔隙率在0.0001～0.001范围内、变量板厚度在5mm～20mm范围内，运用遗传算法对适应度函数进行寻优，如图8所示。

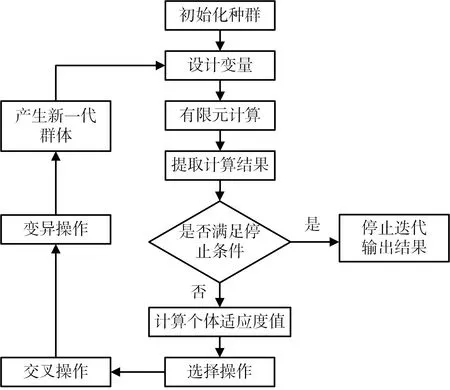
图8 有限元法结合遗传算法的流程图

设定变量数（nvars=2），变量范围（两个变量范围分别设为［0.0001 0.001］和［0.005 0.02］），种群类型为双精度型向量（doubleVector），种群尺度（Population size=50），优良计数（Elite count=2），交叉概率（Crossover fraction=0.8），迁移概率（Migration fraction=0.2）、最大遗传代数（maxgen=15）。

3.4 优化结果

图9显示了遗传算法对微穿孔板透声性能的寻优进程，当板厚度h=0.007m、孔隙率f=0.000214时，适应度函数得到最小值为-0.999662。鉴于传统声学材料的板厚度越薄其透声性能越好，优化前的微穿孔板模型的厚度取区间的最小值5mm，孔隙率取等效阻抗理论推导的最优孔隙率0.0003。图10显示了优化前后微穿孔板透声性能的比较，可以看出微穿孔板透声性能显著提升。

图9 遗传算法寻优进程

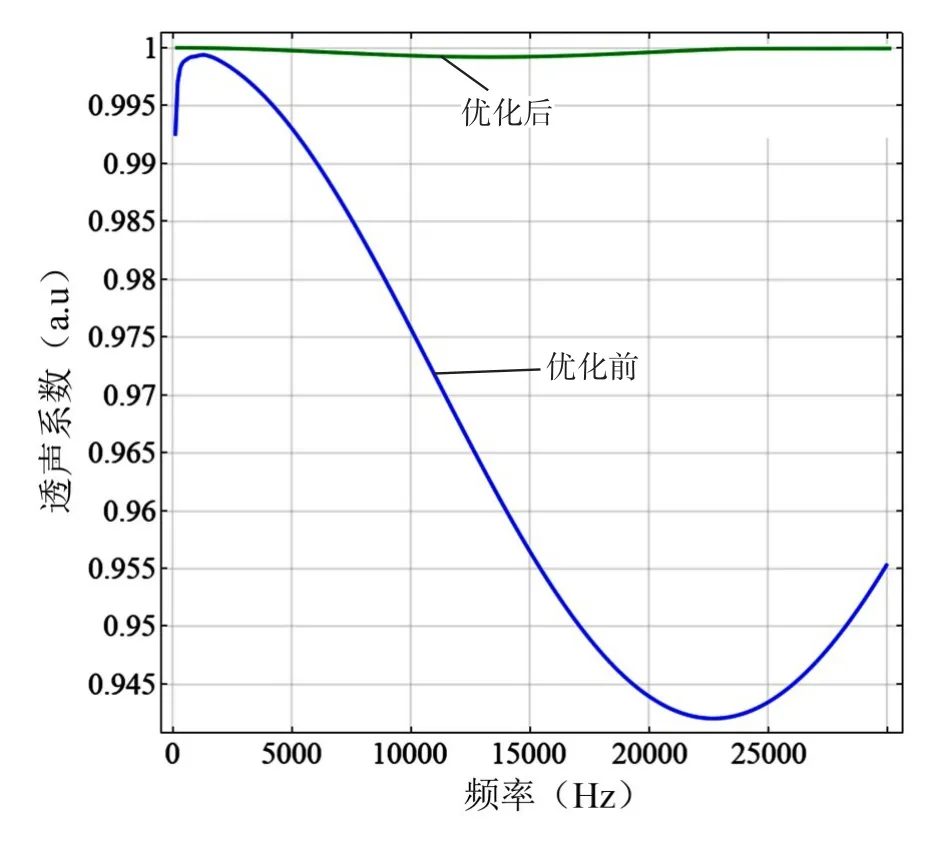
图10 优化前后微穿孔板透声系数对比图

4 结语

1）微穿孔的形状对微穿孔板透声性能的影响不大，四方排列的微穿孔板透声性能略优于三角排列的。

2）得到优化后的四方排列的微穿孔板，孔隙率为0.000214，板厚度为0.007m，可作为水下微穿孔板声超材料设计的依据。