航海雷达训练模拟器中海杂波图像生成算法研究∗

（海军研究院 北京 100161）

1 引言

雷达训练模拟器通过模拟雷达回波界面和操控处理系统，能够实现对各种复杂电磁环境的仿真，达到对雷达兵实装训练的效果，在雷达兵训练中具有重要的意义。对于航海雷达而言杂波最主要的来源是海洋本身，也就是“海杂波”。海杂波不仅受到海浪、风速和天气等自然环境因素影响，而且与雷达工作频率、分辨率、功率、水平波束宽度和擦地角等参数有关［1］，是航海雷达训练模拟器仿真的难点，其仿真程度的好坏直接影响训练的效果。

目前国内外对海杂波的研究不少，但大多数只是针对海杂波幅度分布模型的研究，而对雷达训练模拟器中海杂波图像的研究并不多见，尤其是距离-方位向相关的海杂波图像生成算法。雷达训练模拟器的研究重点是产生逼真的雷达回波界面，本文在结合海杂波的分布特性后，提出了一种训练雷达模拟器中海杂波图像生成算法，该算法采用经典的K分布模型，通过对方位向数据的调制和距离向衰减处理，能够获得逼真的海杂波图像，同时本文算法通过对环境参数的预设可以产生不同的仿真效果，提高雷达操作人员对不同场景的处理能力。

2 海杂波模型

2.1 海杂波幅度K分布模型

Ward等对高分辨率低入射余角的海杂波数据进行了大量的测量分析，其结果表明海杂波幅度分布包含两个分量［2］。第一个是散斑分量，来自于多个散射体的回波矢量叠加，服从瑞利分布。第二个是调制分量，与长波和浪涌结构有关，具有较长的相关时间，服从伽马分布。这与复合K分布模型相一致，K分布是用一个伽马分布的变量来调制复高斯分布的幅度变量。这可以理解为在给定的距离分辨单元内杂波分布以快速瑞利分布起伏，它的平均功率或电压水平随着时间的变化进行慢起伏，分辨单元之间的杂波服从伽马分布［3］。其概率密度统计模型为

式中，x为杂波幅度，Kv(x)为第二类修正贝塞尔函数，为伽马函数，α为尺度参数，v为形状参数。海杂波仿真的实质就是建立满足尺度参数α和形状参数v的K分布模型。

2.2 形状参数及尺度参数估计模型

形状参数和尺度参数是与海洋环境和雷达属性有关的两个参数，准确估计这两个参数是确定仿真模型的基本前提，利用已有的经验模型可以对这两个参数进行估计［4］。

2.2.1 形状参数估计模型

Ward等通过对雷达实验数据分析，给出了一种估计形状参数的经验模型。

其中，φ为入射余角，其范围是0.1°＜φ＜10°，l为角分辨率对应的横距(100＜l＜800)，水平极化时K1=1，垂直极化时，K1=1.7，顺风或逆风时σ=-1/3，侧风时σ=1/3，无风时σ=0。

2.2.2 尺度参数估计模型

在确定形状参数后，可根据下式得到尺度参数α：

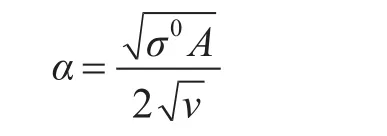
其中，σ0为归一化的雷达散射截面积，σ0=σ/A，其中A为被照射海面面积，σ为被照射海面的雷达截面积。A在小入射余角情况下，公式如下：

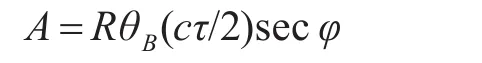
式中，R为雷达至目标的距离，θB为雷达波束宽度，φ为雷达入射余角。

σ0与雷达波长、入射余角、极化、海况等因素有关，针对不同环境条件，σ0建立了很多模型，如SIT、GIT、TSC和HYB模型等，这里给出了一种σ0的计算模型［5］：

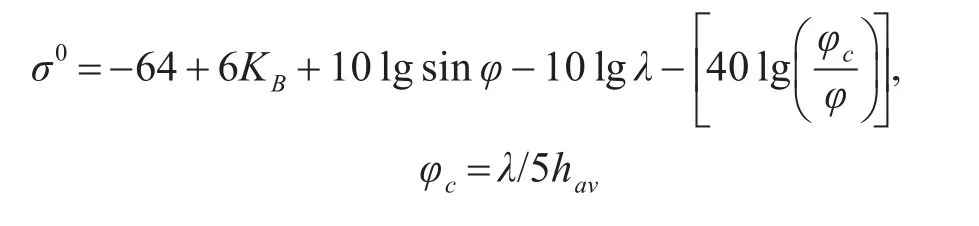
式中，KB为蒲氏海况系数，hav为平均浪高，与海浪有关，均可通过查表获得。

2.3 海杂波的相关性

海杂波的时间相关性是指单个距离单元的杂波在时间上表现出的关联性，由于散斑分量去相关时间远小于调制分量去相关时间，因此在较短时间内认为调制分量基本不变，相关系数为1，回波信号的总体相关性表现为散斑分量的相关性［6］。散斑分量相关性可采用高斯型功率谱来描述，其表达式为

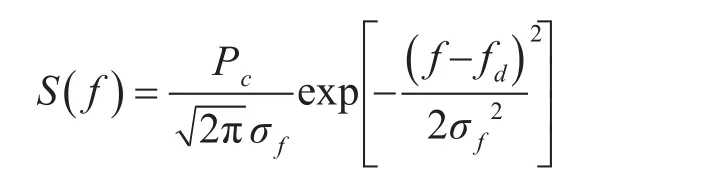
其中，Pc为杂波功率，σf为杂波频谱的均方根值(σf=2σv∕λ)，σv为杂波速度的均方根值，λ为雷达工作波长，fd是多普勒频移，它与风速ω以及风向与视线之间的夹角θ的余弦成比例［7］，即：

k是和海况有关的常数项，一般取3。

空间相关性指相邻距离单元上杂波相互之间的关联性，这里主要指空间距离向相关性，根据杂波散射机理，散斑分量在相邻距离单元是完全去相关的，而与海浪结构有关的调制分量在相邻距离单元内具有明显的相关性，其相关函数可以表示为

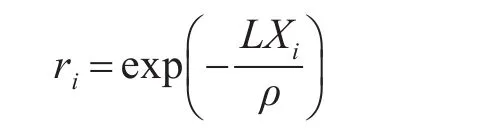
其中，L代表给定的距离分辨率，令N=L/4.2，X1，X2，…，XN代表分辨率L所包含的4.2m的分辨单元，r1，r2，…，rN-1为X1，X2，…，XN之间的相关系数，ρ为相关距离长度，Watts给出ρ的经验公式为

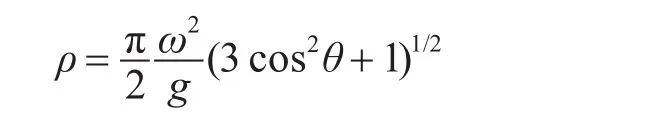
式中，θ为风向与雷达视线夹角，ω代表风速，g是重力加速度。

3 海杂波图像生成算法

3.1 海杂波的方位相关性调制

以上分析了海杂波的时间和空间距离向的相关性，然而对于海杂波图像仿真更关心的是空间方位向的相关性。在时间相关性分析中，默认前提是在短时间内或波束驻留时间内，其调制分量基本不变，相关系数为1，但是在长时间或波束转动一定角度后，其调制分量也发生变化，相关系数不再为1，但也并非完全独立。一个方位单元内的数据可以看成是多个时间单元内数据的累积，因此相邻方位单元的数据存在一定的相关性。图1为真实海杂波的P显图像，从中也可以看出海杂波方位向具有一定相关距离，因此海杂波呈现的是块状，而不是线状或环状。有研究表明方位向相关距离一般是由波束宽度决定的，波束越宽方位向相关距离越大［8］。

图1 真实海杂波P显图像

基于以上的分析和海杂波图像的特点，本文提出了一种距离-方位二维海杂波图像生成算法。该算法采用球不变随机过程法（SIRP）生成K分布数据，同时弱化了海杂波的时间相关性，只在波束驻留时间内取一组海杂波K分布仿真数据，作为该方位向的扫描数据。为了增加方位向的相关性，根据波束宽度的大小，对同一距离向上的多个数据进行线性插值处理，使其在方位向具有一定的相关距离。其仿真过程可用以图2表示。

SIRP法产生K分布数据的基本原理是先产生一个相关的高斯随机过程，然后用具有所要求的单点概率密度函数的随机序列进行调制［9］，其过程如图2所示。W1(k)为随机产生的一维复高斯白噪声序列，k为距离单元个数，H1(z)由Y1(k)的相关函数设计决定，使Y1(k)具有功率谱为高斯谱。R1(k)为一与W1(k)相互独立的一维实高斯白噪声序列，线性滤波器H2(z)为一窄带低通滤波器，使输出Z1(k)具有高度相关性，通过ZMNL变换产生满足伽马分布的序列S1(k)，将序列X1(k)和S1(k)对应元素相乘便得到满足K分布的一维数据。同理共得到n组不同的K分布数据，将其组成一个n×k的二维数据，并对同一距离向的数据进行线性插值处理，最终得到m个方位向的海杂波数据。

3.2 距离衰减

从真实海杂波图像可以看出，海杂波中心区域亮度很高，但随着距离的增加强度逐渐减弱。该现象可以用雷达方程解释，雷达方程描述了雷达参数与目标距离之间的数学关系，理想无耗、自由空间传播时单基雷达方程如下：

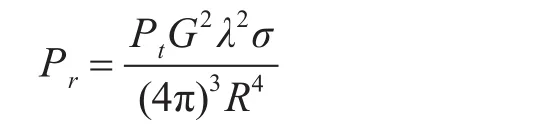
式中，Pr为雷达接收的回波功率，Pt为雷达发射功率，G为天线的增益，σ为目标截面积，λ为波长，R为雷达到目标的距离。从上式可以看出接收功率随雷达到目标距离的4次方衰减，距离越远，衰减得越厉害。该公式同样适用于海杂波，因此要逼真地模拟海杂波，必须对仿真产生的海杂波数据进行距离上的衰减［10～12］。由上式可知，距离衰减模型可以选择如上的指数模型，即在模拟的杂波序列上按距离乘以一个指数衰减的因子。

4 仿真结果

本文利用上述模型对海杂波进行仿真，参数为：雷达波长0.05m，波束宽度2°，距离分辨率3m，水平极化，顺风，海况3，雷达相对风向夹角0°，形状参数估计值1.8，尺度参数估计值3.6。

图3为生成的海杂波某一方位向的数据，该数据符合相关K分布模型，可以看出各距离单元之间存在一定的相关距离。图4为某一距离向的数据，由于经过方位向相关调制，各方位单元之间存在明显的相关性。图5为仿真生成的海杂波方位-距离二维图像，图6为方位-距离-幅值三维图像。图7为进行距离衰减处理后，某一方向距离维数据序列，与图3进行对比可以看出随着距离的增加，幅度明显减弱。

图2 距离-方位二维海杂波图像生成算法框图

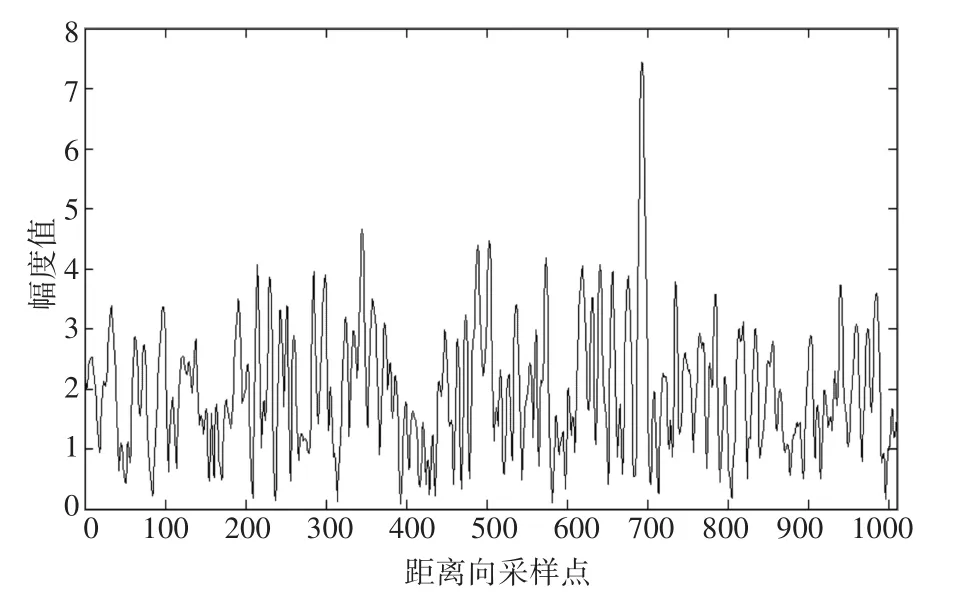
图3 某方位向距离维杂波幅度分布

图4 某距离向方向维杂波幅度分布

图5 方位-距离二维图像

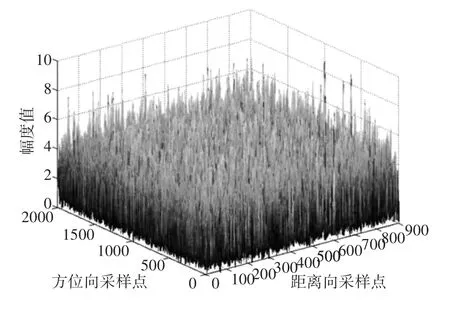
图6 方位-距离-幅值三维图像

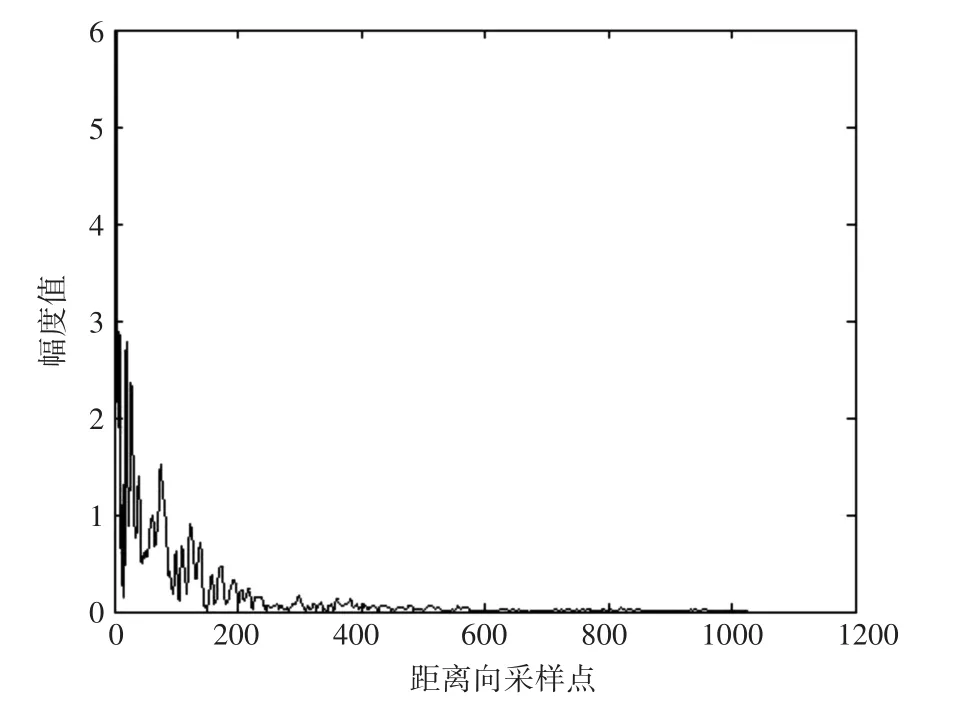
图7 某方位向距离衰减后杂波幅度分布

对生成的海杂波数据进行归一化处理，使其幅度在0～255亮度区间内，输入到雷达显控终端，图8为显控终端显示效果图，图像中心区域亮度较高，周边区域亮度依次减弱，呈现离散的块状，与图1真实海杂波图像相比，本文算法仿真的海杂波图像符合真实海杂波的特点，逼真度较高。

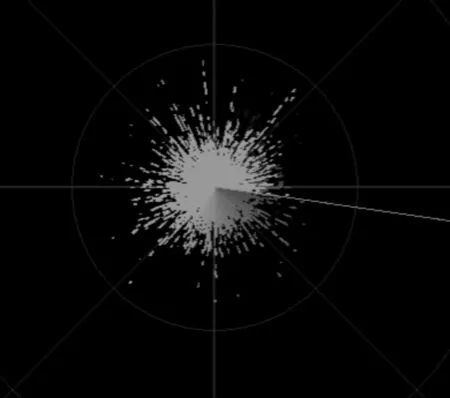
图8 仿真的海杂波P显图像

5 结语

本文结合海杂波的K分布模型，分析了海杂波的时间、空间相关性。针对海杂波图像仿真的特点，利用SIRP法生成符合K分布的随机数据，同时增加方位向相关调制和距离衰减处理，使模型更接近于实际情况。仿真结果表明，本文算法可以较好地模拟不同环境下的海杂波图像，逼真度较高，适用范围广，可满足雷达兵的训练要求。