两关节压力驱动柔性仿生机器鱼的设计与仿真1)

教 柳 张保成 张开升 赵 波

(中国海洋大学工程学院机电工程系,青岛 266100)

引言

水下机器人作为人类探索海洋的主要工具,吸引了越来越多研究机构和学者的目光[1].传统的水下航行器或机器人一般采用螺旋桨式推进装置,这种推进方式能耗噪声大、效率低易伤害到水下生物[2].相比于螺旋桨推进器,自然鱼类在运动过程中机动性高、效率高、噪声低、隐蔽性好且环境扰动小[3-4].鱼类的这些卓越游动性能引起了仿生学等领域许多专家在推进理论和机器鱼模型制作方面的研究兴趣[5].

如何模仿鱼类获得较高的游动性能,众多学者开展了摆动频率、摆动幅度和刚性系数[6-8]等参数对仿生机器鱼游动性能的影响的研究分析,但关于关节数目对仿生机器鱼巡游性能的影响研究与实验并不多.刘军考等[9]进行了电机驱动的单关节尾鳍机器鱼与两关节机器鱼的对比试验,在相同的实验条件下,实验结果表明两关节机器鱼比单关节尾鳍摆动推进的机器鱼具有更高的推进速度.王飞等[10]采用模块化结构设计了“BLRF-I”系列仿鲹科机器鱼,可以更改尾部驱动电机的数量,形成仅舵机关节数量不同的单关节、两关节和三关节仿生机器鱼,进行实验讨论关节数目对机器鱼游动性能的影响.实验表明随着关节数量的增加,仿生机器鱼的巡游速度有效地增大,最小转弯半径减小,巡游稳定性提高.Mart 等[11]使用软驱动材料离子交换聚合金属材料(ionic polymermetal composites,IPMC)作为驱动关节推进仿生机器鱼,通过建立分析模型和计算流体动力学(computational fluid dynamics,CFD)建模方法研究IPMC 制作的单关节尾鳍机器鱼与两关节机器鱼的推进力、弯矩和流场情况,结果表明两关节IPMC 尾鳍比单关节IPMC 尾鳍能够产生更大的推力和更灵活的动作.

受自然界中生物体柔软性的启发,研究者们提出了具有柔软身体的柔性软体机器人概念.不同于机器鱼最常用的电机[12-13]与智能材料的驱动方式[14-16],柔性机器人具有更接近生物的柔软特性,具备机动灵活的运动能力和良好的适应性,高能量密度、低噪声、结构紧凑等优势,因此软体机器人吸引了众多研究人员的关注[17-18].美国麻省理工学院的Andrew D 等[19]在2014 年设计制造了一个能够自主游动的、快速启动逃生的软体气压驱动机器鱼.这款机器鱼采用气压驱动的流动弹性体驱动器(FEA),直接构成鱼身驱动器,由气罐向一侧提供气体增大驱动器内部压强,另一侧快速放气产生鱼体一侧摆动,由气罐的换向充气实现鱼体的连续性换向摆动,此机器鱼可在520 ms 内最大转向100◦.2018 年,同样采用单关节流动弹性体驱动器,这个团队将气压换为水压,提高了持久和耐用性,增加了可调整浮力的深度控制系统,最深可下潜至18 m[20].

MIT 提出的液气压控制的柔性软体机器鱼,具有单关节柔性鱼身,能量转换效率高,鱼身可以产生连续的运动.但是相比于刚体机器鱼,其驱动器结构设计、精确建模、精准控制相对困难,且MIT 的单关节柔性鱼身仅能实现C 型摆动,游动效率虽较刚性机器鱼有所提高,但与自然鱼类相比仍然较低.本文基于上述分析,以液压驱动方式设计两关节柔性机器鱼,采用数值仿真的方法研究了柔性机器鱼的建模和摆动幅值的精准控制,并基于CEL 算法,建立柔性仿生鱼的自主游动流固耦合有限元模型,分析比较单关节、两关节柔性机器鱼的游动性能.

1 柔性机器鱼结构组成与驱动原理

压强驱动方式有气压驱动和液压驱动.气压驱动的动力元器件由气罐和气泵组成,也可由化学剂发生反应持续稳定提供气体.其中,由气罐或是反应剂输出气体作用于柔性鱼身后,无法收回循环利用.由液压驱动的机器鱼,介质是水或油,液压泵和电机为动力元器件.液压泵为正反转、大流量、小体积的双向齿轮泵,液体在鱼身驱动器左右两侧循环利用.

两种驱动方式中,水介质具有不可压缩性、散热快、粘度低且绿色环保的优势.因此本文选择设计水压驱动的柔性机器鱼,其结构如图1 所示.

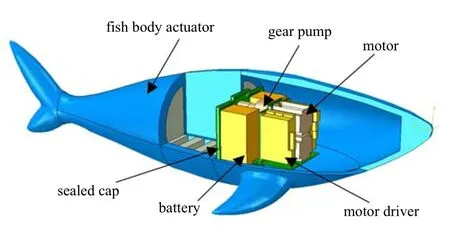
图1 液压驱动柔性机器鱼结构示意图Fig.1 The schematic design of hydraulically driven soft robotic fish

如图2 所示,软体驱动器由3 层结构组成:左侧弹性驱动器,右侧弹性驱动器,中间约束层(c).单侧驱动器由a 中间约束层,b 内嵌流体空腔,c 内嵌肋板,d 外层弹性材料构成.

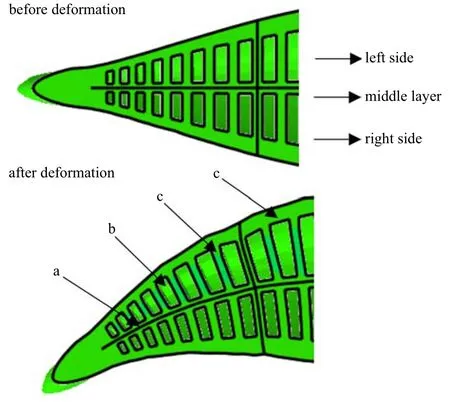
图2 鱼身驱动器变形前后示意图Fig.2 The schematic diagram of the fish body actuator before and after deformation

由柔性驱动器变形图可以看出,其弯曲原理为:两侧驱动器空腔内存在压差时,压强大的一侧驱动器拉伸变形大于另一侧,由于受到中间可弯曲但不能伸长的约束层的轴向方向的约束,压强大的一侧驱动器外侧伸长量大于贴近约束层的伸长量,从而产生偏向中间层方向的弯曲运动.

2 机器鱼建模

2.1 鱼体建模

BCF (body and/or caudal fin) 推进模式机器鱼利用身体的变形带动尾鳍摇摆产生推进力向前游动,游快,效率高,得到更多研究员的关注[21].其中具有月牙形尾鳍的鲔科模式游动效率最高[22],以金枪鱼等硬骨鱼类和鲸鱼、鳖鱼等大型海洋哺乳动物为代表.

鲨鱼在海上被称为霸主,体型较长,粗壮而圆,呈流线型,向后渐细尖而尾基细长,尾鳍为新月形,游动速度快、短时制动爆发力强[23-24].基于上述优点,本文以鲔科鱼类为仿生对象,进行两关节仿生机器鱼的设计与仿真.

仿生机器鱼良好的流线型身体可极大地减小形体阻力,为得到流线型鱼体外形,本文使用三维扫描仪扫描仿真鲨鱼模型,采集到鲨鱼鱼体三维模型.针对研究仿生机器鱼巡游游动性能的目标,对扫描所获得的鲨鱼模型进行优化,将鲨鱼牙齿、眼睛等头部凹凸面改为平滑曲面,去掉背鳍和臀鳍,建模结果如图3 所示.

图3 仿鲨鱼外形的建模模型Fig.3 Shark-like modeling

2.2 关节数的确定

根据文献[25],MIT 制作的液/气压柔性机器鱼只有一个鱼身关节,只能实现鱼身单侧“C” 型摆动,而鲔科鱼类的运动呈现周期性的波动推进行为,根据波动方程[26],鲔科鱼类鱼体在单个周期内不同时刻的波状摆动如图4 所示,因而单关节柔性鱼身不能满足本研究的仿生要求.为使柔性机器鱼摆动姿态贴近真实鲔科鱼,同时又考虑到液压、电子等元件的尺寸和控制因素,本文将机器鱼除鱼头和尾鳍关节外,鱼身分为前后两个关节.

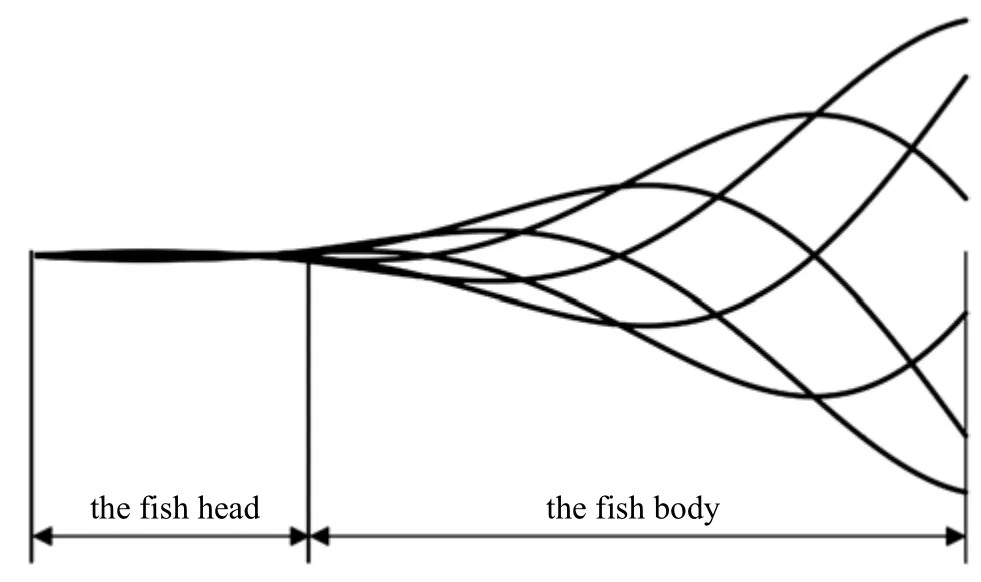
图4 鲔科鱼类波状游动示意图Fig.4 The schematic illustration of wavy swimming of tuna fish

2.3 鱼体驱动器设计

本文的液压驱动柔性机器鱼如图5 所示,由弹性材料制作的鱼身即弹性体驱动器.弹性鱼皮伸长变形是驱动器主要的弯曲动力,因此选择弹性模量较小的材料制作.肋板的结构形似“鱼骨”,不仅起到支撑鱼形的作用,同时在驱动器受压变形时约束鱼身径向尺寸,使鱼体尽可能保持流线型.柔性驱动器中的约束层,选择PP(聚丙烯)材料,可以伴随鱼身产生弯曲运动,但是不产生伸长变形.因鱼身两个关节间时刻存在压力差,在两关节中间处增加一约束层,减小了两关节连接处两侧因内部压差不同造成关节连接处大变形的影响.

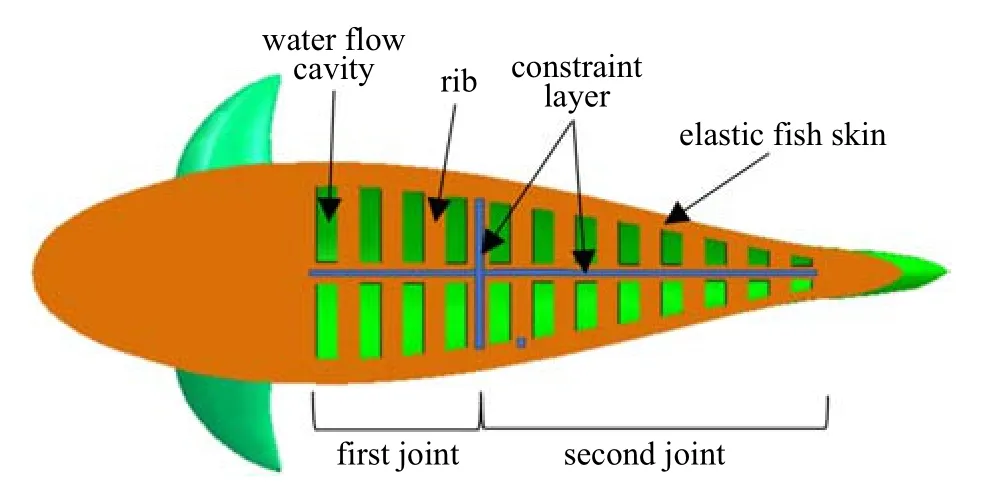
图5 柔性鱼身驱动器剖视示意图Fig.5 The cutaway view of soft fish body actuator

2.4 驱动器压强与弯曲角度

由柔性驱动器驱动原理可知,当结构与材料一定时,驱动器的弯曲角度由施加在内部空腔的压强大小决定.因此,确定施加压强与弯曲角度的关系是精确控制驱动器摆动的关键.由于驱动器复杂的内部结构,建立数学模型分析的方法将大大简化驱动器摆动模型,从而导致分析结果不准确.因此,本文借助有限元仿真软件建立柔性鱼体驱动器模型,分别模拟一、二关节驱动器摆动,计算关节驱动器摆动角度与内部施加压强的关系.以第一关节为例,介绍仿真模型的设定与结果分析,如图6 所示.

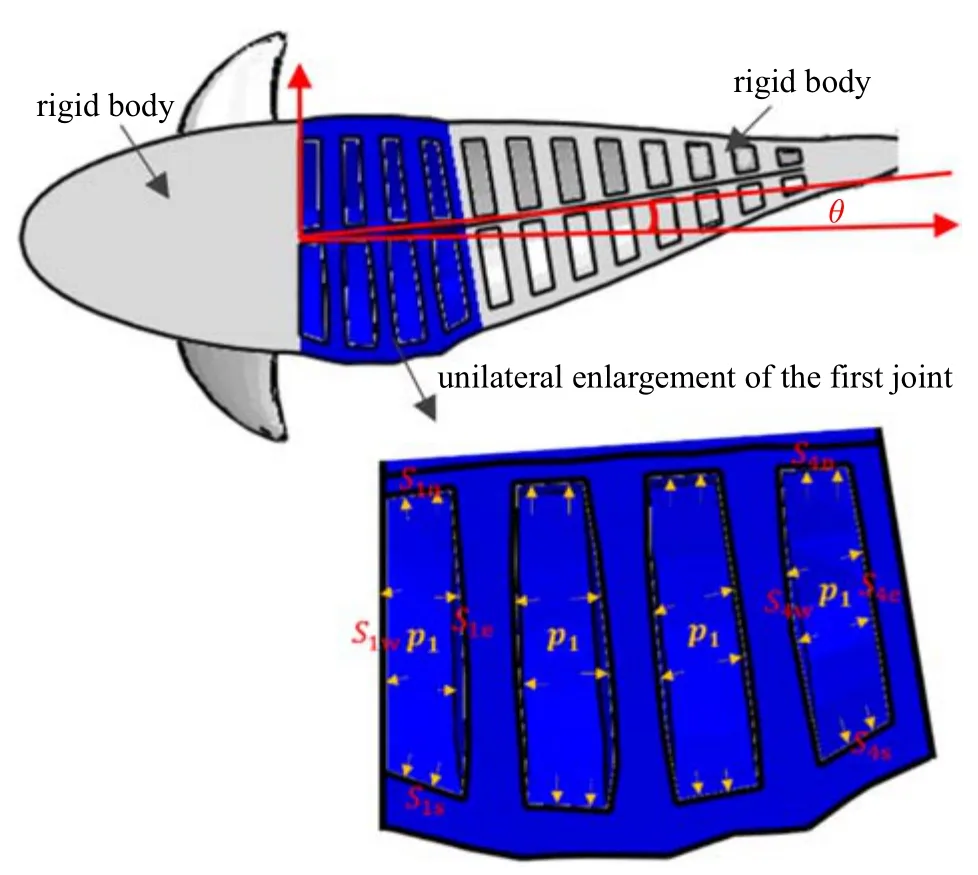
图6 单关节单侧驱动器弯曲示意图Fig.6 Bending diagram of the driver on one side of the single joint

为使仿真能够模拟现实中柔性鱼身驱动器空腔内部水压变化时,驱动器弹性内壁受压导致弹性变形的情况,在有限元仿真前处理载荷设置中,驱动器单侧的每个空腔内4 个表面Siw,Sin,Sie,Sis(i为空腔个数,i=1,2,...,n)均施加垂直于表面向外的压强载荷p1.其中,由于单个关节内空腔连通,因此每个驱动关节内空腔设置同等大小的压强p1.同时,为减少第二关节与鱼头部分对第一关节驱动器摆动的影响,设置为刚体.随着压强p1的增大,第一关节驱动器弯曲角度也逐渐增大,如图7 所示.经分析,鱼身摆动角度θ 与施加压强p1呈二次函数关系

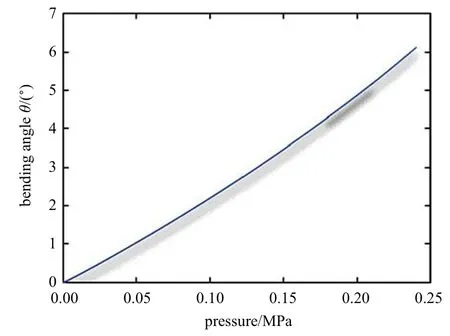
图7 柔性鱼身驱动器弯曲角度与内部施加压强线性关系图Fig.7 Linear relationship between bending angle of soft fish body actuator and internal pressure

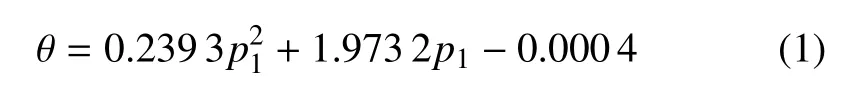
为了验证仿真计算机器鱼柔性驱动器施加压强与摆动角度模型的准确性,对文献[18]中柔性机器鱼采取同样的数值模拟方法进行计算.根据文献中机器鱼模型的外形参数0.34 m×0.051 m×0.07 m,建立机器鱼三维模型,依据文中表1 数据建立内部空腔结构,柔性驱动器材料为Shore A15 硬度的硅胶.将建立的模型导入仿真软件,驱动器空腔内施加55.6 kPa的压强载荷,数值计算鱼身驱动器弯曲角度为40◦,与实验结果的45◦吻合度较高,验证了机器鱼柔性驱动器弯曲角度计算方法的有效性.

2.5 驱动器输出效率

通过进一步分析柔性驱动器的摆动原理并结合仿真模拟验证,如图8 所示,驱动器空腔沿y方向施加的压强p(即表面Sin与Sis)不能使驱动器产生弯曲运动,沿x方向施加的压强p(即表面Siw与Sie)可使驱动器产生弯曲摆动,弯曲角度θ 与空腔内4 个面都施加同等大小压强载荷p产生的弯曲角度θ 相等.

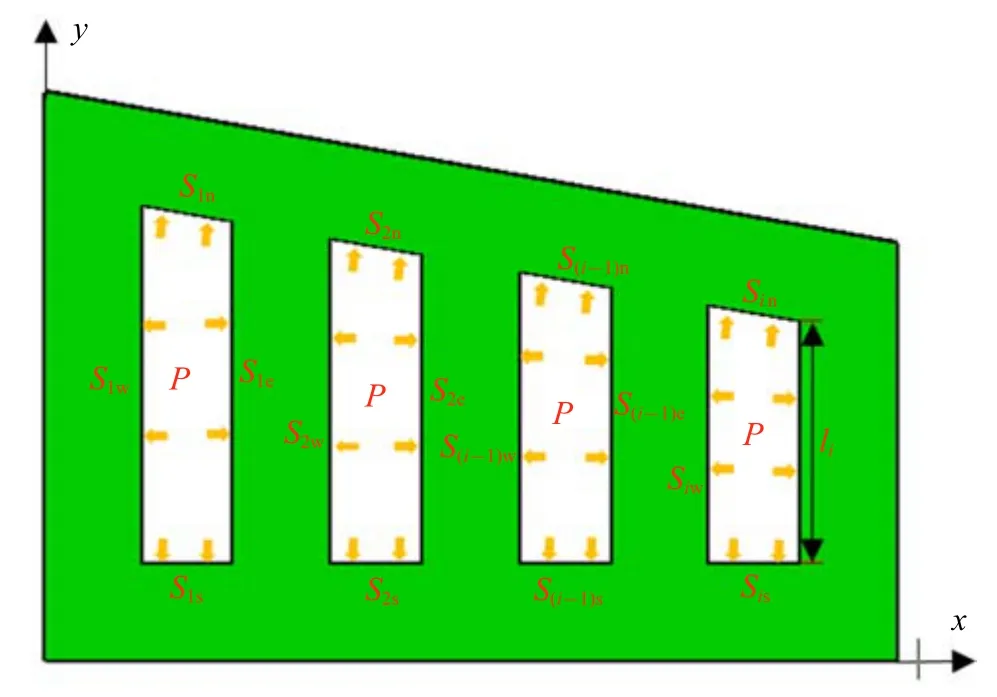
图8 驱动器结构简化示意图Fig.8 Schematic diagram of simplified actuator structure

单个空腔内施加压强p后产生力矩为

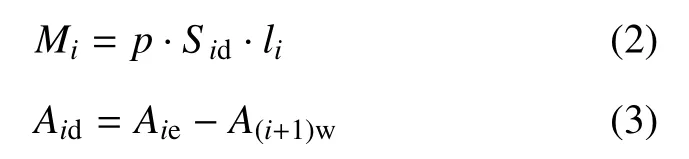
式(3)中,面积差Aid一个空腔Sie面积与后一个空腔S(i+1)w面的面积的差值.

单个空腔做功为

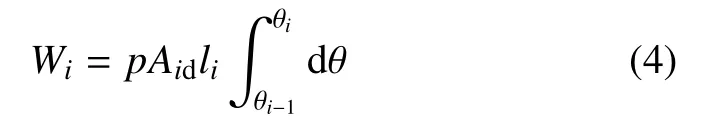
含有n个空腔的柔性驱动器的总功为

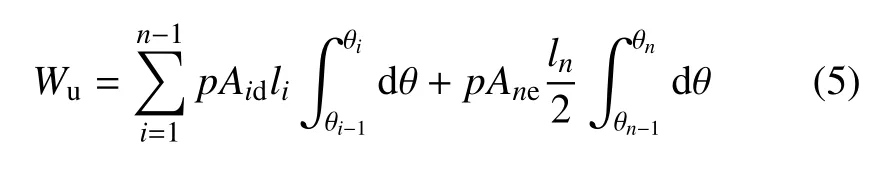
柔性驱动器的弯曲效率为

式中,∆V为驱动器施加压强后的体积变化.

将第一关节单侧驱动器空腔内施加60 kPa 的压强,数值计算得到弯曲角度与体积变化,代入式(6)中,算得弯曲效率为67.3%.

增大柔性驱动器的弯曲效率,从两个方面进行考虑:一是驱动器的材料,二是驱动器的内部结构.对于驱动器的弹性材料,选择硬度较小的弹性材料可以减小能量的消耗,同时在图6 中,明显观察到鱼皮受内部压强产生的鼓包现象,将破坏机器鱼的流线型外形,增大游动阻力.结合真实鱼类鱼骨结构考虑,适当地增大驱动器内部肋板材料的硬度,将有效地减小鼓包现象.

驱动器的内部结构主要包括驱动器空腔与肋板的宽度尺寸,提高柔性驱动器的弯曲效率,即施加同等的压强载荷,增大驱动器弯曲角度.为讨论肋板与空腔尺寸对驱动器摆动的影响,借助数值模拟的方法,设置空腔压强与材料属性一定的条件下,空腔宽度尺寸不变,肋板宽度尺寸分别设为1∼7 mm,进行数值仿真,计算不同肋板宽度尺寸的模型在同等压强下的摆动幅值,结果如图9.从图9 中的数据可以观察出,随着肋板宽度尺寸的增加,摆动幅值逐渐减小.此结论符合真实鱼类鱼骨宽度尺寸远小于鱼肉宽度尺寸.

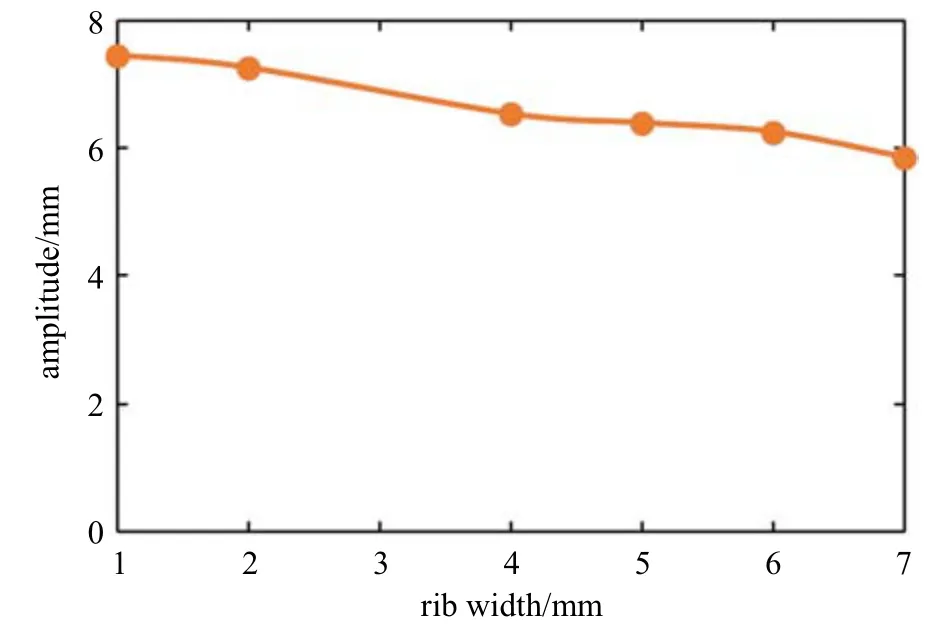
图9 驱动器肋板宽度与摆动幅值的关系Fig.9 The relationship between the width of the rib and the swing amplitude

3 仿生机器鱼的体波分析

3.1 鲔科鱼的体波描述

在游动过程中,鲔科鱼类鱼体的前2/3 部分波动幅值极小,后1/3 部分波动较大,其波动幅值从头部到尾部呈现逐渐增大的趋势,在鱼体后颈部位置波幅达到最大值[27].

根据对身体/尾鳍(BCF)模式推进鱼类的观测结果,采用简单的二次样条曲线来拟合身体波波幅包络线,数学描述鱼体波h(x,t)的表达式为[28]

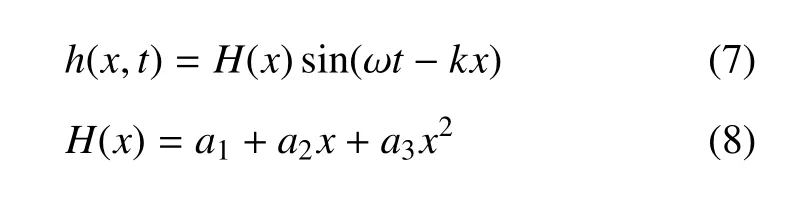
其中,h(x,t)为鱼体的侧向位移(波幅),x为沿鱼体方向的坐标,ω 为鱼体波动的角频率(ω=2π/T),t为时间步,k为鱼体波波数(k=2π/λ),λ 体波波长.式(8)为波幅包络线,a1,a2,a3体的波幅包络线系数,与鱼游动速度、鱼体尺寸、游动姿态等因素有关.

根据生物观测结果,总结鲔科模式鱼体波的参数为k=5.7/L,a1=0.02L,a2=−0.12,a3=0.2/L,其中L为鱼体长度[29].

本文仿鲔科模式机器鱼模型鱼体总长0.5 m,摆动频率为2 Hz,代入式(7)和式(8)式中可得到鱼体波表达式为

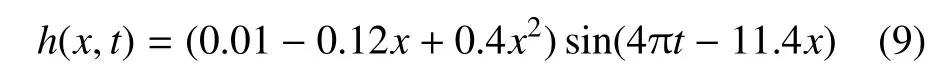
式(9)对应的鱼体波曲线如图10 所示,其中BL(body length)即鱼体体长.

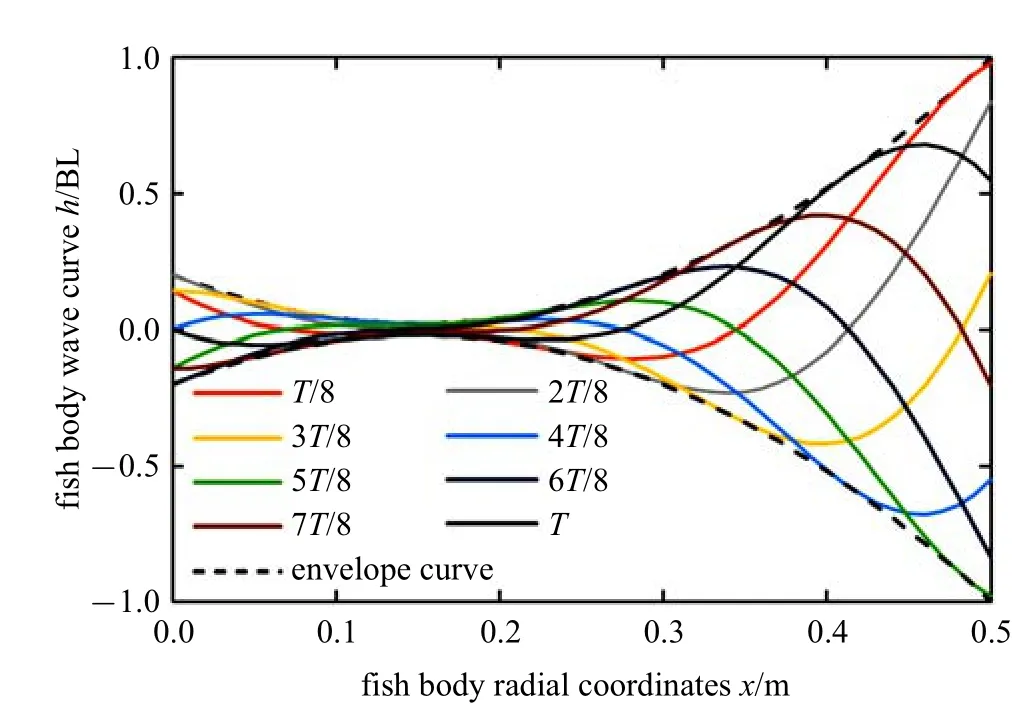
图10 单位摆动周期内鱼体波曲线Fig.10 The body wave curve in unit swing period

3.2 关节运动方程

机器鱼的基本尺寸如图11 所示,除刚性鱼头之外的摆动鱼体部分分为两个关节,刚性鱼头长度为0.18 m,因为鲔科模式机器鱼鱼体最大摆动位移在鱼柄位置,所以摆动鱼体部分长度为0.24 m,尾鳍部分长度为0.08 m,总长0.5 m.

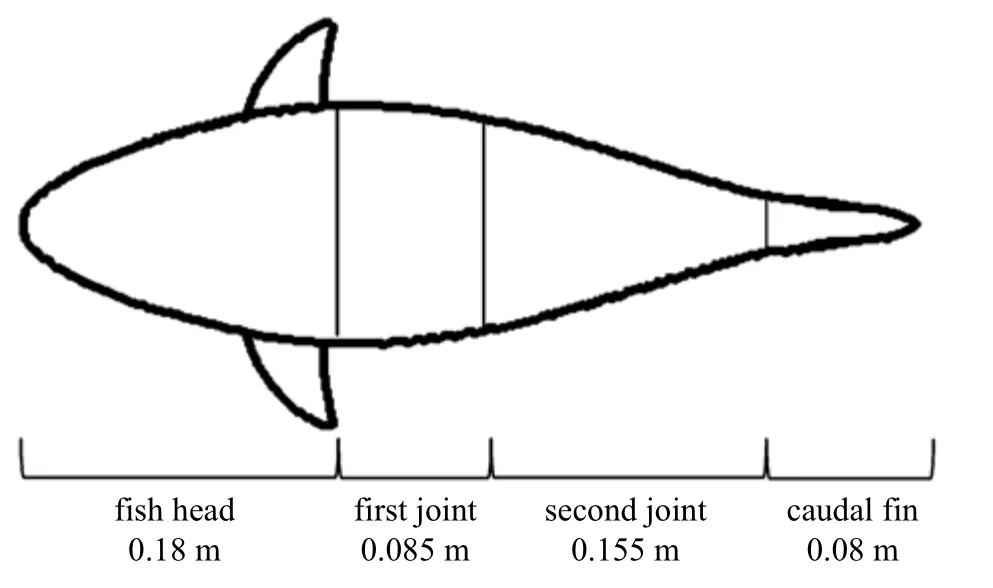
图11 鱼身关节长度示意图Fig.11 The diagram of fish body joint length

将第一、二关节长度代入式(9)中,可得到第一关节运动方程

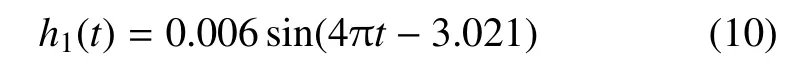
第二关节运动方程

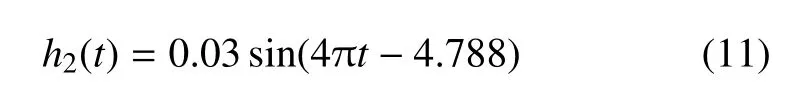
4 动力学仿真

柔性鱼身为复杂非线性结构,传统的理论分析简化了模型,不能直观地研究其游动性能.因此,采用流体仿真软件研究机器鱼,可以建立机器鱼的形体模型和运动模型,研究其运动过程,从而定量地给出时变流场信息,得到接近真实鱼类游动的水动力学参数,进而全面地研究鱼类的推进性能[30].但是,目前大多数鱼类的仿真研究都是将鱼固定,设置流场的来流速度来数值模拟机器鱼的游动,这种非自主性游动的数值模拟方法与自然鱼类的自主游动相差较远.

本文数值模拟采用CEL (耦合欧拉−拉格朗日)算法,将机器鱼模型设为固体,流体为欧拉体进行流固耦合计算,能计算模拟机器鱼模型在流体中自主游动的动态过程,其计算结果较非自主游动的数值模拟方法更贴近真实值.本文基于CEL 算法,建立了柔性仿生鱼的自主游动流固耦合有限元模型,计算驱动器内部施加载荷大小,将自主游动的机器鱼放入欧拉流体中,显式动力分析模块仿真计算机器鱼的游动过程,根据数值模拟结果分析柔性鱼体的摆动情况、游动性能和流场情况.

4.1 材料属性设定

进行柔性机器鱼自主游动的流固耦合仿真计算,需在有限元软件中导入机器鱼和流体域三维模型,完成其基本属性定义.流体域选为欧拉体,参照文献[31] 采用Us-Up Hugoniot 状态方程定义流体域的属性,材料属性参数取值分别为C0=1485 m/s,S=0,γ0=0,ρ=1000 kg/m3,µ=0.001 Pa·s.其中,柔性鱼体驱动器材料选择弹性类橡胶材料,杨氏模量设置为4 MPa,鱼体驱动器内肋板结构的杨氏模量设置为12 MPa.

4.2 膜单元的设定

柔性鱼身驱动器结构的中间约束层厚1 mm,计算过程中厚度过薄易发生应力集中导致网格畸形,影响计算效率.采用膜单元层代替中间薄板,它只传递面上的力,不承受弯矩.膜单元因为不在模型上显示,极大地提高了运算效率[32].

图12 所示的中间膜单元层不仅可以约束鱼身因内部压力增大而产生的沿长度方向拉伸变形,还可减小因受流体剪切力而发生的拉伸变形.图中膜单元层1 即第一关节与第二关节之间的隔离膜单元层,可以减小因关节间的压力差产生的变形.

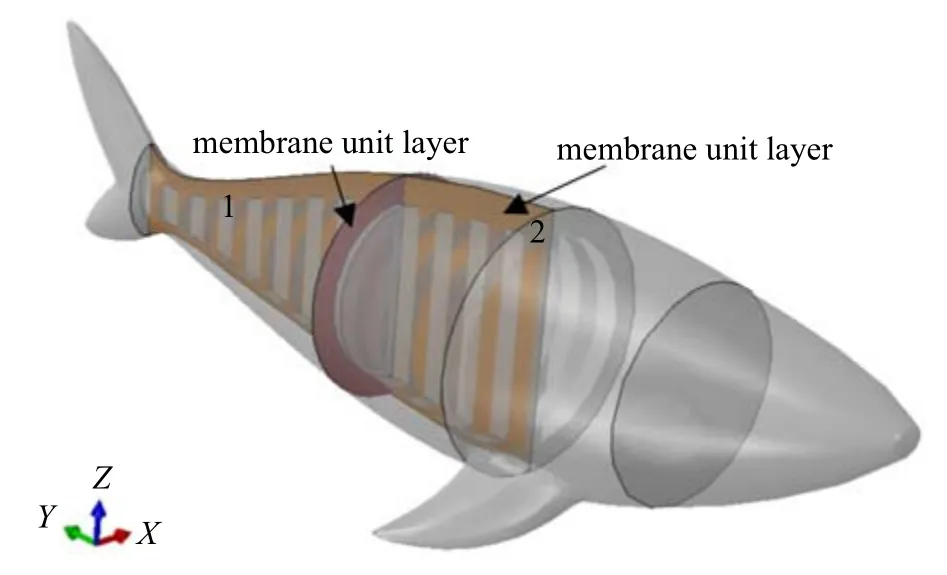
图12 膜单元层示意图Fig.12 The schematic diagram of membrane unit layer

4.3 网格划分与边界条件

机器鱼实验模型外形尺寸0.5 m× 0.108 m ×0.114 m,具有流线型外形和略复杂的内部空腔结构,采用不同尺寸的四面体实体单元自由划分机器鱼实验模型,单元类型为C3D4R,膜单元类型为M3D4R.流体域整体尺寸1.5 m×0.5 m×0.5 m,采用六面体线性欧拉单元(EC3D8R).

并为了更加真实地模拟机器鱼在静水中的游动状态,本文对整个模型施加了重力载荷.然后对流体域设置边界条件:流体域6 个表面上的法向速度为0,保证流体波动后不流出流体域区域.

在机器鱼模型静水中游动流固耦合模拟的过程中,初始流体域充满欧拉材料,即流体的体积分数为1,但是机器鱼模型占据的欧拉体积为空,表明此处的流体材料体积分数为0.

由于仅研究直线巡游性能,本文中机器鱼的胸鳍不产生摆动,尾鳍随着鱼体运动做被动摆动,将头部、胸鳍、尾鳍设置为刚体,并限制头部仅能沿鱼身长度方向运动.

4.4 压强参数

式(8)与式(11)为第一、二关节末端点随时间变化的摆动方程,确定了第一、二关节处摆动幅值按正弦变化且最大值分别为0.006 m、0.03 m.结合关节驱动器弯曲角度与压强的关系,在仿真中分别设定一、二关节驱动器内部压强载荷和载荷幅值曲线.

5 游动性能分析

有限元软件中将两关节机器鱼模型进行自主游动仿真计算,得到机器鱼游动过程如图13 所示.为研究关节数对游动速度的影响,建立了单关节柔性仿生鱼的自主游动流固耦合有限元模型,施加载荷以实现尾鳍处摆动幅值符合波动方程,显式动力仿真计算单关节柔性机器鱼的游动过程如图14 所示.

图13 两关节机器鱼流固耦合仿真结果Fig.13 The fluid-structure interaction simulation results of two-joint robot fish

图14 单关节机器鱼流固耦合仿真结果Fig.14 The fluid-structure interaction simulation results of one-joint robot fish

5.1 摆动姿态

为了清楚地将单关节、两关节柔性机器鱼的摆动姿态与理论鱼体波曲线图10 作比较,在单关节、两关节机器鱼数值模拟结果中,分别截取半个周期内4 个时刻两种机器鱼中间脊骨线处摆动曲线与理论波动曲线,如图15 所示.

由于机器鱼鱼体在一个周期内摆动左右对称,即分析半个周期内的摆动姿态即可.从4 个摆动曲线对比图中,先观察单关节、两关节机器鱼鱼体摆动曲线,观察到由于具有柔性鱼体,单关节、两关节机器鱼的鱼身摆动曲线都为连续性光滑曲线,而不是单一僵硬折线.但是,两关节机器鱼由于前后两个鱼身关节摆动幅度存在相位差,某段时期摆动方向不同,但是关节连接点处过渡平缓,所以姿态不是单侧“C 型曲线”,而是双侧近“S 型曲线”.同时,两个机器鱼鱼身摆动都在尾鳍末尾处达到摆动幅值最大值,单关节机器鱼尾鳍末尾处的最大幅值0.05 m,两关节机器鱼尾鳍末尾处的最大幅值0.052 m.然后,将单关节、两关节机器鱼的鱼身摆动曲线分别与理论曲线做对比,单关节机器鱼仅在关节末端处摆动幅值符合理论值,中间鱼体的摆动幅值与理论值相差较远.两关节机器鱼的摆动姿态基本上与理论曲线保持一致,差距较小,因此两关节机器鱼的摆动曲线更符合理论曲线.

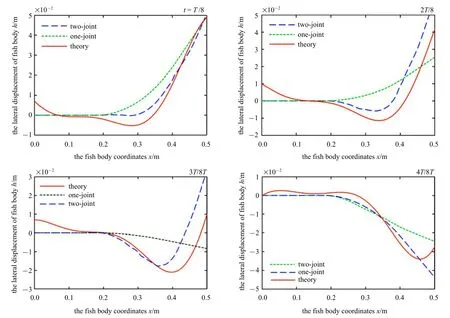
图15 半周期内摆动曲线对比图Fig.15 Comparison of swing curves in half cycle

5.2 速度与效率

分别获得单关节、两关节机器鱼在流场中自主游动6 个周期内的巡游速度时间曲线,如图16 和图17 所示.

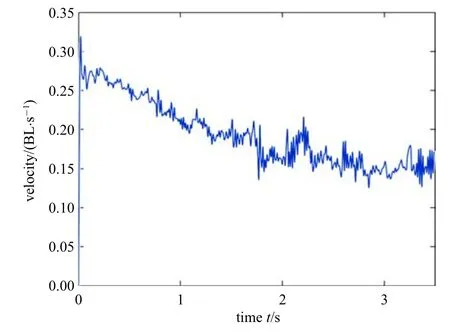
图16 单关节柔性机器鱼周期内摆动曲线Fig.16 The speed-time curve of one-joint soft robot fish during stable swimming

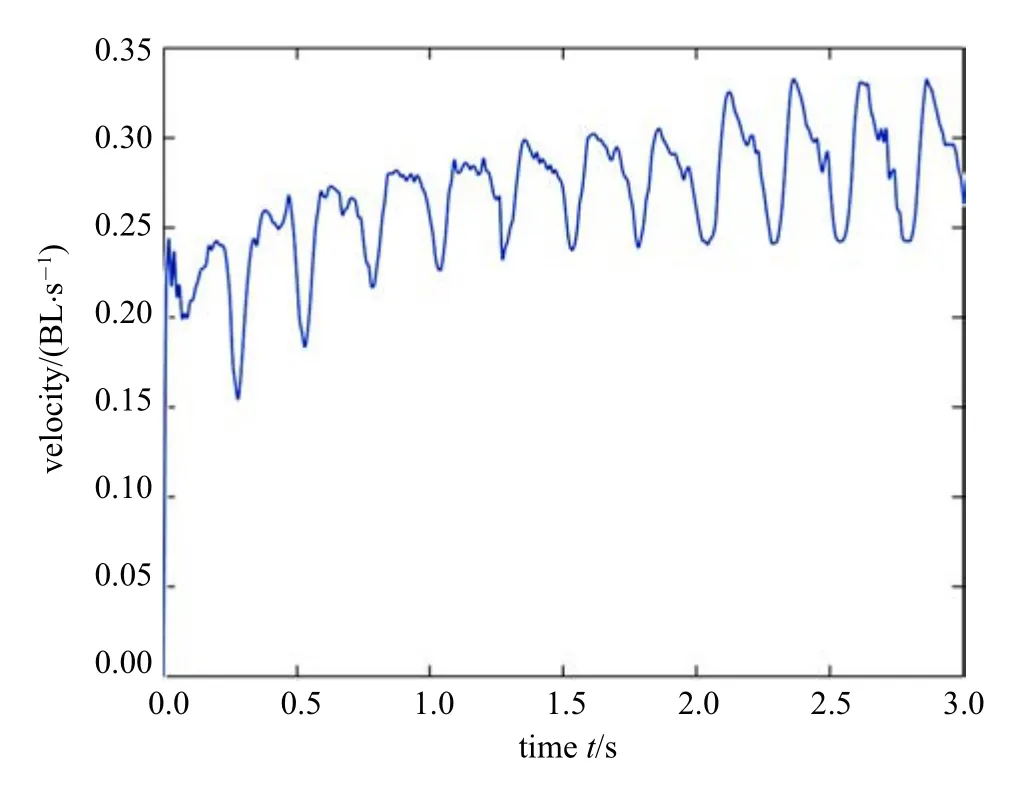
图17 两关节柔性机器鱼周期内摆动曲线Fig.17 The velocity-time curve of two-joint soft robotic fish during stable swimming

本文只分析机器鱼稳定直线巡游状态下的速度,机器鱼因受自身摆动和流场的作用,所以巡游速度不为定值,且随时间有波动.图14 中初期速度为波动下降,稳定阶段平均速度为0.15 BL/s,且速度波动并不随时间作有规律的变化.与文献[19]中单关节液压驱动的柔性机器鱼游动实验结果相吻合,说明本文使用的流固耦合仿真模型对机器鱼游动性能的模拟具有参考价值.

图15 中,开始4 个周期内,两关节机器鱼速度波动性增强,随后呈周期性波动.机器鱼鱼身摆动在鱼尾达到最大幅值处获得最大速度为0.34 BL/s,在鱼身摆动回归中间脊骨线处获得最小速度为0.24 BL/s,平均速度为0.29 BL/s.结果表明,两关节柔性机器鱼比单关节机器鱼在鱼型、摆动频率、尾鳍摆动幅值相同的条件下具有更高的推进速度.

Triantafyllou 研究发现满足斯特罗哈尔数(Strouhal)在0.25 ∼0.35 时,鱼类在运动过程中会产生一系列离散的反向卡门(Karman) 涡街,其诱导的与鱼体运动方向相反的纵向射流对鱼体运动起推进作用[33].也有研究发现采用BCF 模式运动加新月形尾鳍推进的鱼类推进效率高的主要因素之一是鱼体游动的St在0.25∼0.35 之间,可获得最优的推进力和效率[34].因此,本文用无量纲St比较单关节、两关节机器鱼的推进效率[35],其定义式[36]为

式中,f为鱼体摆动频率,Af为鱼体末尾处的最大幅值,U为鱼体平均速度.

计算得单关节机器鱼的St1值为0.667,双关节机器鱼的St2值为0.358.相对于单关节机器鱼,两关节机器鱼的St似认为在0.25∼0.35 之间,其获得最大的推进力,游动效率高于单关节机器鱼.从两关节机器鱼自主游动的仿真结果中截取游动过程中的流场,如图18 所示,可清楚观察到两关节机器鱼游动产生一系列离散的反向卡门漩涡,说明两关节机器鱼有着更大的推进力和效率,同时也符合机器鱼的St值在0.25∼0.35 之间时,将产生一系列离散的反向卡门漩涡的理论[30],在一定程度上验证了所建立的两关节机器鱼流固耦合计算方法的有效性.

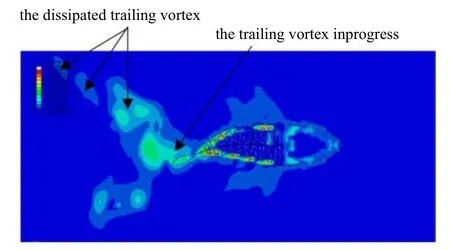
图18 两关节柔性机器鱼自主游动流场图Fig.18 The flow field diagram of autonomous swimming of two-joint soft robotic fish

6 结论

本文中的仿生机器鱼模仿鲨鱼外形及鲔科鱼类的游动姿态,建立了两关节柔性仿生鱼的自主游动流固耦合有限元模型,显式动力分析模块仿真计算机器鱼的游动过程,得出两关节柔性机器鱼游动性能优于单关节柔性机器鱼,其最大速度为0.34 BL/s,平均速度0.29 BL/s,斯特罗哈尔数St2为0.358.结果表明,机器鱼关节数的增加,即其游动姿态越贴近波动方程,机器鱼的游动速度和推进效率越高.一个周期内,机器鱼的游动速度随鱼身摆动而波动变化,且在鱼尾达到最大幅值附近获得最大速度.因此,模拟鱼的游动姿态,使机器鱼的摆动幅值更加贴合波动方程,是提高机器鱼的游动性能的关键方法之一.

本文中柔性机器鱼的液压驱动方式,具有能量转换效率高,运动姿态连续等优点,但是鱼体外部环境压力对鱼身驱动压力影响大,限制了此种驱动方式下机器鱼的下潜深度.